☣

Algorithms

同样动作重复 300 次，肌肉就会有记忆，而一个动作重复 600 次，脊椎就会有记忆。

— 李小龙

ASCII table @

                         +------------------------------------------+
                         |  SP      "               &   '   (   )   |
                         |  )   !   @   #   $   %   ^   &   *   (   |
                         |  0   1   2   3   4   5   6   7   8   9   |
                         +--|---------------------------------------+
                            |
                            |                                           aqaq @ grave
  0         16      32      |48     64      80      96      112
  00        10      20      |30     40      50      60      70
                            |       阿      卡      琳      酱
  NULL     DEL      SP      0       @       P       `       p           |   <-------------- 0
                     !      1       A       Q       a       q           |   <-------------- 1
                     "      2                                           |   <-------------- 2
                     .      .                                           |   <-------------- .
------------------------------------------------------------------------+
    0       1       2       3       4       5       6       7

Usage: ascii [-dxohv] [-t] [char-alias...]
   -t = one-line output  -d = Decimal table  -o = octal table  -x = hex table
   -h = This help screen -v = version information
Prints all aliases of an ASCII character. Args may be chars, C \-escapes,
English names, ^-escapes, ASCII mnemonics, or numerics in decimal/octal/hex.

Dec Hex    Dec Hex    Dec Hex  Dec Hex  Dec Hex  Dec Hex   Dec Hex   Dec Hex
  0 00 NUL  16 10 DLE  32 20    48 30 0  64 40 @  80 50 P   96 60 `  112 70 p
  1 01 SOH  17 11 DC1  33 21 !  49 31 1  65 41 A  81 51 Q   97 61 a  113 71 q
  2 02 STX  18 12 DC2  34 22 "  50 32 2  66 42 B  82 52 R   98 62 b  114 72 r
  3 03 ETX  19 13 DC3  35 23 #  51 33 3  67 43 C  83 53 S   99 63 c  115 73 s
  4 04 EOT  20 14 DC4  36 24 $  52 34 4  68 44 D  84 54 T  100 64 d  116 74 t
  5 05 ENQ  21 15 NAK  37 25 %  53 35 5  69 45 E  85 55 U  101 65 e  117 75 u
  6 06 ACK  22 16 SYN  38 26 &  54 36 6  70 46 F  86 56 V  102 66 f  118 76 v
  7 07 BEL  23 17 ETB  39 27 '  55 37 7  71 47 G  87 57 W  103 67 g  119 77 w
  8 08 BS   24 18 CAN  40 28 (  56 38 8  72 48 H  88 58 X  104 68 h  120 78 x
  9 09 HT   25 19 EM   41 29 )  57 39 9  73 49 I  89 59 Y  105 69 i  121 79 y
 10 0A LF   26 1A SUB  42 2A *  58 3A :  74 4A J  90 5A Z  106 6A j  122 7A z
 11 0B VT   27 1B ESC  43 2B +  59 3B ;  75 4B K  91 5B [  107 6B k  123 7B {
 12 0C FF   28 1C FS   44 2C ,  60 3C <  76 4C L  92 5C \  108 6C l  124 7C |
 13 0D CR   29 1D GS   45 2D -  61 3D =  77 4D M  93 5D ]  109 6D m  125 7D }
 14 0E SO   30 1E RS   46 2E .  62 3E >  78 4E N  94 5E ^  110 6E n  126 7E ~
 15 0F SI   31 1F US   47 2F /  63 3F ?  79 4F O  95 5F _  111 6F o  127 7F DEL

Cheatsheet @

// misc

    using namespace std;

// typedef

    typedef int Point;
    typedef struct { Point x, y; } Point2d;
    typedef Point2d Triangle[3];    // Triangle tri;    // 6 ints inside
    typedef Point2d (*FuncPtr)( Point2d p1, Point2d p2 );

// pointers

    int *array = new int[5];
    delete[] array;

    int *i = new int;
    delete i;

// vector

    #include <vector>
    vector<vector<int> > mat( row, vector<int>(col, 0) );
    vector<int> vec;
    vec.reserve(10);
    vec.resize(5);
    vec.clear();
    vector<int>().swap(vec);

// char manip

    #include <ctype>
    int isalnum(    int c   );
    int isalpha(    int c   );
    int isascii(    int c   );
    int isblank(    int c   );
    int iscntrl(    int c   );
    int isdigit(    int c   );
    int isgraph(    int c   );
    int isprint(    int c   );
    int ispunct(    int c   );
    int isspace(    int c   );
    int isxdigit(   int c   );

// equal?

    int i;
    i%2 == 0
    i%2 != 0

    double a, b;
    fabs(a-b) < 1e-9

// memory

    #include <stdlib.h>                 // malloc
    #include <string.h>                 // memcpy
    malloc( size    );
    calloc( nmemb, size );
    realloc(  ptr, size );
    free(   ptr     );

    memset( buf, value, numbytes );
    memcpy( dst, src, size );
    int strcmp(     s1,     s2  );
    int strncmp(    s1,     s2,     n );
    char *strcpy(   char *dest, const char *src );
    char *strncpy(  char *dest, const char *src, size_t n );

        char buf1[9] = "01234567";
        char buf2[6] = "abcde";
        strncpy( buf1, buf2, 4 );
        printf( "%s\n", buf1 ); // "abcd4567"

       char * strncpy( char *dest, const char *src, size_t n ) {
           // at most n char will be altered
           size_t i;
           for( i = 0; i < n && src[i] != '\0'; ++i ) {
               dest[i] = src[i];
           }
           for( ; i < n; ++i ) {
               dest[i] = '\0';
           }
           return dest;
       }

    char *strchr(   const char *s, int c );
    char *strrchr(  const char *s, int c );

    memcmp( s1, s2, nbytes ); // -1, 0, 1

// file io

    #include <stdio.h>
    FILE *fp = fopen(filename, "r");
    while( 2 == fscanf( fp, "%d %s", &index, buf ) ) { ... }
    fclose(fp);
    size_t fread(        void *ptr, size_t size, size_t nmemb, FILE *stream );
    size_t fwrite( const void *ptr, size_t size, size_t nmemb, FILE *stream );

    #include <fstream>
    ifstream file( filename.c_str(), ifstream::in );
    ifstream file;
    file.open( filename.c_str(), ifstream::in );
    if ( !file )                    { ... }
    if ( !file.is_open() )          { ... }

    string line;
    while ( getline(file, line) )   { ... }
    sort( line.begin(), line.end() );

    string s( n, '0' );

    ofstream file;
    file.open( "example.txt" );
    file << "Writing this to a file.\n";
    file.close();

// string

    sscanf( string.c_str(), format, ...)
    int fscanf ( FILE * stream, const char * format, ... );
    fgets( buf, sizeof(buf), stdin );
    sprintf( str, %d", num );

    #include <sstream>
    string input;
    istringstream stream(input);
    while( stream >> i ) { ... }

    string output;
    ostringstream ss;
    ss << i << d << s;
    output = ss.str();

// atoi, etc

    #include <stdlib.h>
    double      atof(  const char *str );
    int         atoi(  const char *str );
    long        atol(  const char *str );
    long long   atoll( const char *str );

// stl

    fill(   v.begin(),  v.end(),    -1 );
    fill_n( v.begin(),  v.size(),   -1 );
    fill_n( &v[0],      v.size(),   -1 );

    reverse_iterator<string::iterator>  r = s.rbegin(); ++r;
    string::reverse_iterator            r = s.rbegin(); ++r;

    for (auto i : v)
    for (auto const &n : nums)

    vector<char> vec( str.begin(), str.end() );

    binary_search( haystack.begin(), haystack.end(), needle) );
    search( haystack.begin(), haystack.end(), needles.begin(), needles.end() ) != haystack.end();

    int i = 32;
    vector<int> vi = { 10, 21, 32, 43 };
    auto it1 = search( vi.begin(), vi.end(), &i, &i+1 );
    printf( "index: %d, value: %d\n", (int)distance(vi.begin(), it1), *it1 );
    //  index: 2, value: 32

    string s = "two";
    vector<string> vs = { "zero", "one", "two", "three" };
    auto it2 = search( vs.begin(), vs.end(), &s, &s+1 );
    printf( "index: %d, value: %s\n", (int)distance(vs.begin(), it2), it2->c_str() );
    //  index: 2, value: two

    struct Sum {
        Sum(): sum{0} { }
        void operator()(int n) { sum += n; }
        int sum;
    };
    vector<int> nums{1, 2, 5};
    for_each( nums.begin(), nums.end(), [](int &n){ n++; } );   // 2, 3, 6
    Sum s = for_each( nums.begin(), nums.end(), Sum() );
    int s = for_each( nums.begin(), nums.end(), Sum() ).sum;    // 11

    min( 1, 9999 );
    max( 1, 9999 );
    pair<const T&, const T&> minmax( const T& a, const T& b, Compare comp );

    vector<int>::iterator result = max_element( v.begin(), v.end() );
    int idx = distance( v.begin(), result );
    int val = v[idx];

    int nums[50];
    int highest = *max_element( nums, nums+50 );

    auto iter = prev( it, 2 );
    auto iter = next( it, 2 );
    advance( it, 2 );

    swap( a, b );

    partial_sum( first, last, d_first );

    for( deque<int>::iterator it = q.begin(); it != q.end(); ++it )
        cout << *it << endl;
    }

    #include <iterator>
    auto lower = lower_bound(data.begin(), data.end(), 4);
    auto upper = upper_bound(data.begin(), data.end(), 4);
    copy(lower, upper, std::ostream_iterator<int>(std::cout, " "));

    transform( s.begin(), s.end(), s.begin(), [](unsigned char c) { return toupper(c); } );

    str1.erase( remove(str1.begin(), str1.end(), ' '), str1.end() );
    auto last = unique(v.begin(), v.end());
    v.erase( last, v.end() );

    // stack
        #include <stack>
        stack<int> s;
        s.push( 7 );
        s.pop();
        s.top();
        for( stack<int> dump = s; !dump.empty(); dump.pop() ) {
            cout << dump.top() << '\n';
        }

    // queue
        #include <functional>                                           // std::greater
        #include <queue>

        // priority_queue
        priority_queue<int> pq;
        priority_queue<int, std::vector<int>, std::greater<int> > pq;   // default is less<T>
        pq.push( 7 );                                                   // like stack
        pq.pop();
        pq.top();

        // queue
        queue<int> q;
        q.push( 7 );
        q.pop();
        q.front();      q.back();

    // set
        // set
        #include <set>
        set<int> s;
        s.insert( 5 );
        s.erase(  5 );
        for( auto i : s ) { cout << i << "\n"; }
        for( set<int>::iterator it = s.begin(); it != s.end(); ++it ) { cout << *it << "\n"; }


        // unoreder_set
        #include <unordered_set>
        unordered_set<int> us;
        us.insert( 5 );
        us.erase(  5 );
        for( auto i : s ) { cout << i << "\n"; }
        for( unordered_set<int>::iterator it = s.begin(); it != s.end(); ++it ) { cout << *it << "\n"; }

    // map
        // map
        #include <map>
        map<string, int> m;
        ++m[key];       // 第一次使用也不用创建，因为没有这个 key 的时候，会自动生成并把 int 初始化为 0。
                        //                  std::map<char, int> m;
                        //                  std::cout << m['a'] << "\n";    // 0
                        //                  ++m['b'];
                        //                  std::cout << m['b'] << "\n";    // 1
                        //                  m['c'] = 5;
                        //                  std::cout << m['c'] << "\n";    // 5
        if( m.find(2) != m.end() )      { ... }
        if( m.count(2) )                { ...}

        map<string, int> m = {{"one", 1}, {"two", 2}};
        m["zero"];
        for( auto p : m ) { cout << p.first << " -> " << p.second << "\n"; }
        for( map<string, int>::iterator it = m.begin(); it != m.end(); ++it ) { cout << it->first << " -> " << it->second << "\n"; }

        // unordered_map
        #include <unordered_map>
        unordered_map<string, int> m = {{"one", 1}, {"two", 2}};
        m["zero"];
        for( auto p : m ) { cout << p.first << " -> " << p.second << "\n"; }
        for( unordered_map<string, int>::iterator it = m.begin(); it != m.end(); ++it ) { cout << it->first << " -> " << it->second << "\n"; }

// flags

    #include <climits>
    #include <cstddef>
    CHAR_MAX,                   UCHAR_MAX
    SHRT_MAX,                   USHRT_MAX
    INT_MAX,                    UINT_MAX
    LONG_MAX,                   ULONG_MAX
    LLONG_MAX,                  ULLONG_MAX
    DBL_MAX
    FLT_MAX

FAQ @

刷题刷到什么程度可以去面试了呢？

lintcode 70% 题目刷两遍， 60% 题目做到 bug free，就比较好啦。

前端工程师 / 数据科学家需要刷题么？

当然需要啦，60% 考算法，40% 考相关背景技术或项目经验。

在哪里可以找到面经?

glassdoor, 一亩三分地，themianjing.com, mitbbs，等等。

先刷题还是先看面经捏？

一般建议先刷一点题目，然后再去看面经。这样轻松一点，遇到会的题目就跳过，不会的题目好好想一想，时间允许还可以实现一下。如果时间很紧张了，建议一边刷题一边看面经。

哪里可以投简历？找内推？

投简历： indeed，monster, hired.com, linkedin, readyforce.com，以及各大公司官网。
找内推： mitbbs，一亩三分地, linkedin

TODOs & Notes @

(left+right)/2 和 left + (right-left)/2 除了在负数的时候不同之外，后者还不会越界。

How to compile && run

# compile
g++ code.cpp -o code --std=c++11
# run
cat input.txt | ./code

fib, fac @

fibonacci. factorial.

0.

我的算法学习之路 - Lucida @

基友在人人发百度实习内推贴，当时自我感觉牛逼闪闪放光芒，于是就抱着看看国内 IT 环境 + 虐虐面试官的变态心理投了简历，结果在第一面就自己的师兄爆出翔：他让我写一个 stof（字符串转浮点数），我磨磨唧唧半天也没写出完整实现，之后回到宿舍赶快写了一个版本发到师兄的邮箱，结果对方压根没鸟我。

这件事对我产生了很大的震动——

原来自己连百度实习面试都过不去。
原来自己还是一个编程弱逼。
原来自己还是一个算法菜逼。

我也很 happy，因为没想到自己写的库居然比 MS 的还要快几十倍，同时小十几倍。

从这个事情之后我变得特别理解那些造轮子的人——你要想想，如果你需要一个飞机轮子但市场上只有自行车轮子而且老板还催着你交工，你能怎么搞。

实习实习着就到了研二暑假，接下来就是求职季。

求职季时我有一种莫名的复仇感——尼玛之前百度实习面试老子被你们黑的漫天飞翔，这回求职老子要把你们一个个黑回来，尼玛。

现在回想当时的心理实属傻逼 + 幼稚，但这种黑暗心理也起了一定的积极作用：我丝毫不敢有任何怠慢，以至于在 5 月份底我就开始准备求职笔试面试，比身边的同学早了两个月不止。

我没有像身边的同学那般刷题——而是继续看书抄代码学算法，因为我认为那些难得离谱的题面试官也不会问——事实上也是如此。

编程珠玑 & 更多的编程珠玑

没听说过这两本书请自行面壁。前者偏算法理论，后者偏算法轶事，前者提升能力，后者增长谈资，都值得一读。

证明简单代码段的正确性是一个很神奇的技能——因为面试时大多数公司都会要求在纸上写一段代码，然后面试官检查这段代码，如果你能够自己证明自己写的代码是正确的，面试官还能挑剔什么呢？

之后就是各种面试，详情见之前的博客，总之就是项目经历、【纸上代码】加【正确性证明】这三板斧，摧枯拉朽。

MIT 教授 Erik Demaine 则更为直接：

If you want to become a good programmer, you can spend 10 years programming, or spend 2 years programming and learning algorithms.

refs and see also

我的算法学习之路 - Lucida

9 个 offer，12 家公司，35 场面试，从微软到谷歌，应届计算机毕业生的 2012 求职之路 @

外企（Google、MS、Yahoo 等） > 国内互联网（阿里、腾讯、百度、网易等） > 企事业单位（基本不考虑）

我的微软 mentor 曾提到过，我的实习面试表现一般，但后来表现出的动手能力大大超出之前面试的预估，而有些面试表现很出色，问题对答如流的选手，入职之后反而不是很理想，至少没有达到面试时发挥出的水准。

这说明一个问题，就是笔试面试，准备和不准备会差异很大。如果你的简历不是那么 NB，那就只能靠笔试和面试的加分撑场面。身边经常有同学纳闷这样代码都编不利索的傻屌都能进 MS 为什么我不能进，答案往往很简单：人家比你多准备了一个月。平时电脑上写程序可能很利索，笔试面试时在纸上写写试试你就知道什么叫拙计。

IT 公司的笔试和面试的题量都不大（相对于企事业单位和银行动辄上百道选择题的题量，算是很少），一般十几道选择题，三四道大题就算题量很大。但计算机的东西实在又是太多，程序设计、数据结构、算法设计、操作系统、体系结构、编译原理、数据库、软件工程等分支，编译的话太难（一千个码农里也没几个人能在纸上写一个最基础的递归下降 LLParser），软件工程、体系结构、数据库这些太水（不是说这些分支没用，而是它们很难考察，尤其对应届生来说这些都是些文字游戏，比如说面向对象的三要素五原则，有个鸟用），这么一排除，再把数据结构和算法设计一合并，就剩下程序设计、算法和操作系统。没错，这三项搞定，国内外 IT 公司通杀。

Tips

重温之前自己做过的靠谱项目，并总结里面的关键难题和解决思路
重读 Programming Pearls 和 More Programming Pearls，并完成所有课后题
独立解决编程之美里面的题目（国内不少企业选题用的这本书）
完成 Careercup 里 Amazon、Google 和 Microsoft 这三个分类下面的前 20 页面试题
完成 TopCoder 的数十道 D1L2~D2L1 难度区间的算法题目
重读 Computer Systems a Programmer’s Perspective 的关键章节，回顾里面的关键点

从七月底开始一直到十一月，花了接近四个月，很多东西都是一边面试一边准备：面试->发现盲点->修复盲点。

简历

篇幅。控制在一页以内。倒不是说不能写两页，而是 HR 没时间看两页这么多。而且就我看过的几百封简历而言，凡是超过两页的没一个靠谱，有这么高的先验概率，HR 才没工夫一个个筛，反正中国有的是人。
重点。一定要有重点，做到让 HR 通过简历在 20 秒内确定你靠不靠谱。可以用加黑字体进行视觉引导。
别字。千万不要出现错别字，别字简历一般直接干掉。一页的简历都能出问题，一般不会靠谱。

但是研发的算法题是一样的，最后一道算法题很有意思，我花了一个多小时才想到利用组合数学里面的知识（多元一次方程非负解）给出设计方案，后来和面试官聊这道题时他们也挺吃惊，因为我的方案比他们的答案还要优化。

微软：

题型只有二十道不定项选择题，难度较难，要求在一小时四十分钟完成。难度较难，覆盖面非常广，从设计模式，算法分析，代码阅读到 C++ 语言特性，甚至连冷门的函数式程序设计语言都有涉及。
微软的笔试题目 BT 之处在于其独特的积分机制：答对了加分，不答无分，答错了倒扣。这就使得很多 ds 答完试卷感觉自我良好但实际已经被倒扣出翔。以最后一道题为例，答对了加 7 分，答错倒扣 13 分，相当于一下子损失 20 分。所以微软的笔试题会做就得做对，不会做就别蒙，要不更惨。
此外，微软的笔试题是英文的，加上时间比较短，有些人题都读不完，有些 ds 连 functional language 是什么都不知道，自然败的很惨。

从笔试题可以明显看出，国外的大型 IT 公司（比如雅虎，微软和谷歌等）并不在意你现在的 skill set，而更看重你的 potential，因此题目大多很基础，并具备相当的深度，以确保你对 CS 有深刻的理解并能够走的很远；而国内的 IT 公司（比如百度、搜狗和人人等）更看重你现在的 skill set，因此会出现不少语言特性，OS 操作之类的具体题目，以确保你能够以尽快的速度上手干活，至于能发展到啥程度他们就不 care 了。

考虑到几乎所有的公司都有编程题目，也就是在纸上写代码，这里推荐几本相关书籍：

1 Elements of programming style 2nd，写出良好风格的代码。纸上代码一般不长，但短短几行代码往往可以看出这个人的水准，风格很差的代码往往会被 pass 掉。
2 Algorithm design manual 2nd，作为非 ACM 出身的码农，这本书比算导实用很多，课后题也很实在，对回溯，动态规划这些编程技巧讲的非常清楚。
3 C interfaces and implementation，无论是面试还是笔试，一般都会用 C 写程序，这本书包含大量的工业级 C 代码，绝佳的参考和模仿素材。

最后推荐下 Elements of programming 和 Structure and interpretation of computer programs，这两本书难度很高，需要大量的时间阅读，不适合临场阅读准备，但读过后，写出的代码绝逼会上两个层次，这里我就不多介绍了。

refs and see also

9 个 offer，12 家公司，35 场面试，从微软到谷歌，应届计算机毕业生的 2012 求职之路 - Luc - 博客园

白板编程浅谈——Why, What, How ♥️ @

技术面试中的问题大致可以分为 5 类：

编码

考察面试者的编码能力，一般要求面试者在 20 ~ 30 分钟之内编写一段需求明确的小程序（例：编写一个函数划分一个整形数组，把负数放在左边，零放在中间，正数放在右边）；
设计

考察面试者的设计/表达能力，一般要求面试者在 30 分钟左右内给出一个系统的大致设计（例：设计一个类似微博的系统）
项目

考察面试者的设计/表达能力以及其简历的真实度（例：描述你做过的 xxx 系统中的难点，以及你是如何克服这些难点）
脑筋急转弯

考察面试者的『反应/智力』（例：如果你变成蚂蚁大小然后被扔进一个搅拌机里，你将如何脱身？）
查漏

考察面试者对某种技术的熟练度（例：Java 的基本类型有几种？）

因为几乎所有的当面（On-site）技术面试均要求面试者在白板上写出代码，而不是在面试者熟悉的 IDE 或是编辑器中写出。

为什么要进行白板编程（WHY）

除了判定面试者的开发效率，白板编程还有助于展示面试者的编程思路，并便于面试者和面试官进行交流
让面试者在解题的过程中将他/他的思维过程和编码习惯展现在面试官面前，以便面试官判定面试者是否具备清晰的逻辑思维和良好的编程素养
如果面试者陷入困境或是陷阱，面试官也可以为其提供适当的辅助，以免面试陷入无人发言的尴尬境地

什么是合适的白板编程题目（WHAT）

下面是一些问滥的编程问题：

编程之美书里的所有题目；
July 的算法博客中的绝大多数题目（包括面试 100 题中的所有题目）；
leecode 里的大部分题目；

需要注意的是，尽管过于直接的算法题目不适合面试，但是我们可以将其进行一点改动，从而使其变成合理的题目，例如稳定划分和二分搜索计数（给出有序数组中某个元素出现的次数）就不错，尽管它们实际是快速排序和二分搜索的变种

这些题目往往要求面试者拥有极强的算法背景，尽管算法问题是否过于复杂因人而异

需要 aha! moment（参考脑筋急转弯）
需要使用某些『非主流』数据结构/算法才能求解
耗时过长（例如实现红黑树的插入/删除）

应该问什么问题

不止一种解法 @

良好的编程问题都会有不止一种解法。这样面试者可以在短时间内给出一个不那么聪明但可实现的『粗糙』算法，然后通过思考（或面试官提示）逐步得到更加优化的解法，面试官可以通过这个过程观察到面试者的思维方式，从而对面试者进行更客观的评估。

以【数组最大子序列和】为例，它有一个很显然的 O(n3) 解法，将 O(n3) 解法稍加改动可以得到 O(n2) 解法，利用分治思想，可以得到 O(nlogn) 解法，除此之外它还有一个 O(n) 解法。（编程珠玑和数据结构与算法分析 C 语言描述对这道题均有非常精彩的描述，有兴趣的朋友可以自行阅读）
考察点明确
延伸问题

良好的编程问题应拥有延伸问题。延伸问题既可以应对面试者背题的情况，也可以渐进的（Incremental）考察面试者的编程能力，同时还保证了面试的延续性（Continuity）。

如何进行白板编程（HOW）

面试者应该做什么

面试前 ♥️
- 拥有扎实的数据结构/算法基础
- 知道如何利用 前条件/不变式/后条件 这些工具编写正确的程序
- 能够在白板（或纸上）实现基本的数据结构和算法（如果 1 和 2 做到这一步是水到渠成）
- 在 leetcode 或 careercup 上面进行过练习，了解常见的技术面试题目（我个人不鼓励刷题，但在面试前建立起对面试题的『感觉』非常重要）

面试中

理解题目，确认需求

使用实例数据验证 (testing is important) 自己的程序 @

Given range [2, 3, 4, 5, 1] and pivot 3

[ 2, 3, 4, 5, 1 ]
  ^             ^
 p,b            e

[ 2, 3, 4, 5, 1 ]
     ^          ^
    p,b         e

[ 2, 3, 4, 5, 1 ]
     ^  ^       ^
     p  b       e

[ 2, 3, 4, 5, 1 ]
     ^     ^    ^
     p     b    e

[ 2, 1, 4, 5, 3 ]
        ^     ^ ^
        p     b e

[ 2, 1, 4, 5, 3 ]
        ^       ^
        p      b,e

Now we have all [0, p) < 3 and all [p, e) >= 3

他们在面试时会自带一根细笔迹的水笔，专门用于白板编程。

不会做怎么办

至少先给出一个暴力（Brute force）解法
寻找合适的数据结构（例如栈 / 队列 / 树 / 堆 / 图）和算法（例如分治 / 回溯 / 动态规划 / 贪婪）
从小数据集开始尝试
如果还是没有头绪，重新考虑题目的前条件，思考是否漏掉了条件（或是隐含的条件）
如果 3 分钟过后还是没有任何思路，请求面试官提示，不要觉得不好意思—— 经过提示给出答案远强于没有答案

个人不建议面试者在面试之后把题目发到网上，很多公司在面试前都会和面试者打招呼，有的会签订 NDA（Non Disclosure Agreement）条款以确保面试者不会泄露面试题目。尽管他们很少真的去查，但如果被查到那绝对是得不偿失。

我自己在面试之后会把面试中的编程题目动手写一遍（除非题目过于简单不值得），这样既能够验证自己写的代码，也可以保证自己不会在同一个地方摔倒两次。

  东瀛修炼绝世武功（在校刻苦学习技术）；
  远赴中原挑战群雄（即将毕业开始求职）；
  拔剑削枯枝作战书（撰写简历进行面试）；
  惊动中原第一高手（简历 / 面试得到赏识）；
  海上决战名扬天下（得到 Offer 搞定工作）。

refs and see also

白板编程浅谈——Why, What, How - Lucida

知其所以然（以算法学习为例） @

徐宥在讨论中提到，这种策略的本质可以概括成“让未知世界无机可乘”。它是没有“弱点的”，答案的任何一个分支都是等概率的。反之，一旦某个分支蕴含的可能性更多，当情况落到那个分支上的时候你就郁闷了。比如猜数字游戏最糟糕的策略就是一个一个的猜：是 1 吗？是 2 吗？… 因为这种猜法最差的情况下需要 64 次才能猜对，下界非常糟糕。二分搜索为什么好，就是因为它每次都将可能性排除一半并且无论如何都能排除一半（它是最糟情况下表现最好的）。

如何称的指导原则有了，构造一个称的策略就不是什么太困难的事情了。首先不妨解释一下为什么最直观的称法不是最优的——6、6 称：在 6、6 称的时候，天平平衡的可能性是 0。刚才说了，最优策略应该使得天平三种状态的概率均等，这样才能三等分答案的所有可能性。

在堆排里面有大量这种近乎无效的比较，因为被拿到堆顶的那个元素几乎肯定是很小的，而靠近堆顶的元素又几乎肯定是很大的，将一个很小的数和一个很大的数比较，结果几乎肯定是“小于”的，这就意味着问题的可能性只被排除掉了很小一部分。

这就是为什么堆排比较慢（堆排虽然和快排一样复杂度都是 O(NlogN) 但堆排复杂度的常系数更大）

本来呢，MacKay 写那篇文章是想用信息论来解释为什么堆排慢，以及为什么快排也慢的。MacKay 在他的文章中的解释是，只有提出每种答案的概率都均等的问题，才能获得最大信息量。然而，仔细一想，其实这里信息论并不是因，而是果。这里不需要用信息论就完全能够解释，而且更明白。信息论只是对这个解释的一个形式化。

另外，这几天我重新把 TAOCP 第三卷 (第二版) 翻出来看了看 Knuth 怎么说这个问题的, 发现真是牛大了：

先说性能：

pp148, section 5.2.3 说：

When N = 1000, the approximate average runiing time on MIX are

160000u for heapsort

130000u for shellsort

80000u for quicksort

这里, Knuth 同学发现一般情况下 heapsort 表现很不好. 于是，在下文他就说，习题 18 (pp156, 难度 21)

(R.W.Floyd) During the selection phase of heapsort, the key K tends to be quite small, so that nearly all the comparisons in step H6 find K<K_j. Show how to modify the algorithm so that K is not compared with K_j in the main loop of the computation, thereby nearly cutting the average number of comparisons in half.

答案里面的方法和 DMK 的方法是一样的。(我觉得 DMK 是看了这个论文或者 TAoCP 的) 这里说 by half，就正好和快排差不多了。

再说信息论分析：

在 5.3.1 (pp181) 高爷爷就说, “排序问题可以看成是一个树上的鸟儿排排站的问题. (还特地画了一棵树), 下一段就说, 其实这个也有等价说法, 就是信息论, 我们从称球问题说起…”

然后后面一直讲信息论和最小比较排序…

高爷爷真不愧是姓高的，囧 rz..

refs and see also

有哪些学习算法的网站推荐？ @

所以, 倾情推荐:

http://oj.leetcode.com LeetCode Online Judge

只要每道题都可以保证 3 遍以内过, 所有湾区工作 entry level 随便挑. 涉及到的基本都是 Linked List, DP, BST 这样的简单数据结构或者算法题.

不难, 但是对于初学算法的人来说, 能熟练运用这些算法已经很不容易了. 可以说是非常不容易了. 因为太多的人眼高手低.

所以说, 还是做题最有效. 就算是你看了算法导论的前几页, 知道了什么是 insertion sort, 不见得你写出来的代码就是对的. 不信的话, 打开 Insertion Sort List, 试试能不能通过.

refs and see also

有哪些学习算法的网站推荐？ - 知乎

1.

A Bit of Logic @

【Axiom】	【Signification】
Associativity (结合律) of addition	`u + (v + w) = (u + v) + w`
Commutativity `[kə,mjuːtə'tɪvɪtɪ]` (交换律) of addition	`u + v = v + u`
Identity element of addition	There exists an element 0 ∈ V, called the zero vector, such that `v + 0 = v` for all v ∈ V.
Inverse elements of addition	For every v ∈ V, there exists an element −v ∈ V, called the additive inverse of v, such that v + (−v) = 0

XOR: either one, but not both

Symbol	Operator
`&`	bitwise AND
`\|`	bitwise inclusive OR
`^`	bitwise XOR (eXclusive OR)
`<<`	left shift
`>>`	right shift
`~`	bitwise NOT (one’s complement) (unary)

refs and see also

九章算法班/强化班 (JiuZhang) ♥️ ♥️ ♥️ @

没有报这个班（关键是穷 ==），但从这个列表（syllabus），可以制定自己的复习内容。

（我把 ACM-Cheatsheet 和 AOAPC 两本书的内容整合过来了。） @

ACM-Cheatsheet @

ditched. have been merged into JiuZhang.

chap2. Linear List
chap3. String
chap4. Stack and Queue
chap5. Tree
chap6. Searching
chap7. Sorting
chap8. Brute Force
chap9. BFS
chap10. DFS
chap11. Divide & Conquer
chap12. Greedy
chap13. DP
chap14. Graph
chap15. Math Methods and Models
chap16. Big Integer
chap17. Functionalities

aoapc-book @

ditched. have been merged into JiuZhang.

第一部分：语言篇

第 1 章，程序设计入门
第 2 章，循环结构程序设计
第 3 章，数组和字符串
第 4 章，函数和递归

第二部分：基础篇

第 6 章，数据结构基础
第 7 章，暴力求解法

第三部分：竞赛篇

第 8 章，高级算法设计
第 9 章，动态规划初步
第 10 章，数学概念与方法
第 11 章，图论模型与算法
第 12 章，高级专题

Lessons for Whom? @

无算法基础，或算法基础薄弱，不系统
希望求职 Facebook, Google, Linkedin, Airbnb, Uber 等硅谷知名企业
面试经验少或无面试经验，不知道与面试官如何正确的沟通和展现自己
网上练习题目那么多，不知道该从哪些题开始准备
获取最新面试动向
认识一起找工作的其他小伙伴

✂️ 2016/07/31 上午 9:30:00 1. Introducing Algorithm Interview && Coding Style【免费试听】 @

通过 strStr 这一道常见面试题讲解面试中的常见误区 @

用常规的循环来做的话，复杂度是 O(mn)，参考代码如下：

int strstr(char *str, char *sub)
{
    if ( !str || !sub) { return -1; }

    int nstr = strlen(str);
    int nsub = strlen(sub);
    if ( nstr < nsub ) { return -1; }

    int len = nstr - nsub;
    int i,j;
    for ( int i = 0; i <= len; ++i ) {          // 如果两个字符串等长, 至少要比较一下, 对吧.
        int j;
        for ( j = 0; j < nsub; ++j ) {
            if ( str[i+j] != sub[j] ) {
                break;
            }
        }
        if ( j == nsub ) {
            return i + 1;
        }
    }
    return -1;
}

误区？：

结果正确 v.s. 条理清晰
代码风格
分析、描述问题
边界检查？
难度？

这个博客很好的说明了面试官的考察思路：

从武侠小说到程序员面试 - Lucida @

回到程序员面试，大多数笔试 / 面试题目都可以在网上找到，而一些公司在招聘时为了省事甚至直接到网上搜题，这就导致看似很高的程序员面试门槛实际变的很低——得到一份还不错的工作并不需要花一两年系统的学习计算机技术，而只需一两个月到 leetcode、 CareerCup 以及未名求职版刷题目。原本很有区分度的算法题目也变的毫无价值——谁知道你是自己想出来的还是背出来的。就像轻功水上漂，谁知道你是真的功力深厚，还是提前在水底打了暗桩。

接下来我会问面试者能不能改善它的可读性（Readability）: input - 32 -> input - 'a' + 'A'

其实就是用 'a' <= input && input <= 'z' 替代 input >= 'a' && input <= 'z' —— 这个技巧源自于代码大全，代码大全里面专门有一节讲解如何编写可读的布尔表达式。从这里我可以看出这些面试者都没有读过代码大全，考虑到代码大全几乎是程序设计的必读书籍，我可以推断出这些面试者很可能没有阅读习惯，而不阅读的程序员一般都不会太出色。

接下来我会询问能不能进一步提升性能: table

如果面试者能提到他是从 C 语言标准库里面学到这个技巧，加 10 分 :–)

有的面试者会想到使用宏： #define TO_UPPER(input) convert_table[input] 这时我会询问宏的优点和缺点，以及在这里使用宏会不会有错误。总之就是确定面试者确实理解宏，而不是从哪里（比如编程之美之类的面试书籍）背了一个答案出来。

接下来，让我们回顾这道简单的题目都考察了哪些点：

函数的概念（而不是写在 main 里）;
缩进和命名（而不是拼音）；
使用可读的字面量（‘a’ - ’A’而非 32）；
API 设计（当 to_upper 接收到非小写字母字符应该返回什么？0？报错？还是返回原值？考虑到 to_upper 的应用场景是把一个字符串中的小写字母转化为大写，返回原值显然更合理）；
是否有阅读习惯（至少可以看出你有没有认真的读过代码大全）；

是否读过 C 标准库源码（指出 toupper 数组实现的出处）； @

/* Note: this is decimal, not hex, to avoid accidental promotion to unsigned */
#define _toupper(__c) ((__c) & ~32)             // turn off one bit, -32
#define _tolower(__c) ((__c) | 32)              // turn on  one bit, +32

enum {                                          // flags
    __ctype_upper = (1 << 0),
    __ctype_lower = (1 << 1),
    __ctype_digit = (1 << 2),
    __ctype_xdigit = (1 << 3),
    __ctype_space = (1 << 4),
    __ctype_print = (1 << 5),
    __ctype_punct = (1 << 6),
    __ctype_cntrl = (1 << 7),
};

extern const unsigned char __ctypes[];          // lookup table

__ctype_inline int islower(int __c)
{
    return __ctypes[__c + 1] & __ctype_lower;
}

__ctype_inline int isupper(int __c)
{
    return __ctypes[__c + 1] & __ctype_upper;
}

__ctype_inline int toupper(int __c)
{
    return islower(__c) ? _toupper(__c) : __c;
}

__ctype_inline int tolower(int __c)
{
    return isupper(__c) ? _tolower(__c) : __c;
}

/usr/lib/syslinux/com32/include/ctype.h @

/*
 * ctype.h
 *
 * This assumes ISO 8859-1, being a reasonable superset of ASCII.
 */

#ifndef _CTYPE_H
#define _CTYPE_H

#include <klibc/extern.h>

#ifndef __CTYPE_NO_INLINE
# define __ctype_inline static __inline__
#else
# define __ctype_inline
#endif

/*
 * This relies on the following definitions:
 *
 * cntrl = !print
 * alpha = upper|lower
 * graph = punct|alpha|digit
 * blank = '\t' || ' ' (per POSIX requirement)
 */
enum {
    __ctype_upper = (1 << 0),
    __ctype_lower = (1 << 1),
    __ctype_digit = (1 << 2),
    __ctype_xdigit = (1 << 3),
    __ctype_space = (1 << 4),
    __ctype_print = (1 << 5),
    __ctype_punct = (1 << 6),
    __ctype_cntrl = (1 << 7),
};

extern const unsigned char __ctypes[];

__ctype_inline int isalnum(int __c)
{
    return __ctypes[__c + 1] & (__ctype_upper | __ctype_lower | __ctype_digit);
}

__ctype_inline int isalpha(int __c)
{
    return __ctypes[__c + 1] & (__ctype_upper | __ctype_lower);
}

__ctype_inline int isascii(int __c)
{
    return !(__c & ~0x7f);
}

__ctype_inline int isblank(int __c)
{
    return (__c == '\t') || (__c == ' ');
}

__ctype_inline int iscntrl(int __c)
{
    return __ctypes[__c + 1] & __ctype_cntrl;
}

__ctype_inline int isdigit(int __c)
{
    return ((unsigned)__c - '0') <= 9;
}

__ctype_inline int isgraph(int __c)
{
    return __ctypes[__c + 1] &
    (__ctype_upper | __ctype_lower | __ctype_digit | __ctype_punct);
}

__ctype_inline int islower(int __c)
{
    return __ctypes[__c + 1] & __ctype_lower;
}

__ctype_inline int isprint(int __c)
{
    return __ctypes[__c + 1] & __ctype_print;
}

__ctype_inline int ispunct(int __c)
{
    return __ctypes[__c + 1] & __ctype_punct;
}

__ctype_inline int isspace(int __c)
{
    return __ctypes[__c + 1] & __ctype_space;
}

__ctype_inline int isupper(int __c)
{
    return __ctypes[__c + 1] & __ctype_upper;
}

__ctype_inline int isxdigit(int __c)
{
    return __ctypes[__c + 1] & __ctype_xdigit;
}

/* Note: this is decimal, not hex, to avoid accidental promotion to unsigned */
#define _toupper(__c) ((__c) & ~32)
#define _tolower(__c) ((__c) | 32)

__ctype_inline int toupper(int __c)
{
    return islower(__c) ? _toupper(__c) : __c;
}

__ctype_inline int tolower(int __c)
{
    return isupper(__c) ? _tolower(__c) : __c;
}

__extern char *skipspace(const char *p);
__extern void chrreplace(char *source, char old, char new);

#endif /* _CTYPE_H */

数组的运用（使用转换表）；
了解宏，以及宏的危害（使用宏）；
是否背过这道题（在第一时间给出使用数组 + 宏的最优方案）；
EOF 以及 C 标准库风格。

接下来我还会要求面试者测试这个函数并给出测试代码，这里恕不赘述。

我的答案是，排除对算法的盲目崇拜，因为这样的题目非常难出，而且对面试官的要求又很高，所以绝大多数面试官都选择去网上搜题目而不是自己出题这条捷径。殊不知这条捷径正是人才招聘失败的源泉——优秀的程序员因为没有背题而被拒绝，而水平平平的“裘千丈”们却因为背过题目而被录用，这些录用的“裘千丈”们又会用同样的方式招聘下一批更加糟糕的“裘千丈”，讽刺至级。

从面试者的角度来说，出题的目的？: qualified.

tell them you are professional
tell them you are smart
tell them you match

思路：

可以用 bitmap
可以排序，然后用 i，j 来判断。

还可以用牛逼闪闪的 KMP 算法。

KMP ♥️ @

KMP 算法是 Knuth、Morris 和 Pratt 在 1976 年发表的。它的基本思想是，当出现不匹配时，就能知晓一部分文本的内容（因为在匹配失败之前它们已经和模式相匹配）。我们可以利用这些信息避免将指针回退到所有这些已知的字符之前。这样，当出现不匹配时，可以提前判断如何重新开始查找，而这种判断只取决于模式本身。

推荐网上的几篇比较好的博客，讲的是部分匹配表 (partial match table) 的方法（即 next 数组）:

字符串匹配的KMP算法 - 阮一峰的网络日志 @

移动位数 = 已匹配的字符数 - 对应的部分匹配值

“部分匹配”的实质是，有时候，字符串头部和尾部会有重复。比如， “ABCDAB”之中有两个“AB”，那么它的“部分匹配值”就是 2（“AB”的长度）。搜索词移动的时候，第一个“AB”向后移动 4 位（字符串长度 - 部分匹配值），就可以来到第二个“AB”的位置。

字符串匹配的 Boyer-Moore 算法 - 阮一峰的网络日志

在一个字符串中找到第一个只出现一次的字符。如输入 abaccdeff，则输出 b。

    A   B   C   D   A   B   D
    0   0   0   0   1   2   0

"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例，
-   "A"的前缀和后缀都为空集，共有元素的长度为 0；
-   "AB"的前缀为 [A]，后缀为 [B]，共有元素的长度为 0；
-   "ABC"的前缀为 [A, AB]，后缀为 [BC, C]，共有元素的
    长度 0；
-   "ABCD"的前缀为 [A, AB, ABC]，后缀为 [BCD, CD, D]，
    共有元素的长度为 0；
-   "ABCDA"的前缀为 [A, AB, ABC, ABCD]，后缀为
    [BCDA, CDA, DA, A]，共有元素为"A"，长度为 1；
-   "ABCDAB"的前缀为 [A, AB, ABC, ABCD, ABCDA]，后缀
    为 [BCDAB, CDAB, DAB, AB, B]，共有元素为"AB"，长
    度为 2；
-   "ABCDABD"的前缀为 [A, AB, ABC, ABCD, ABCDA, ABCDAB]，
    后缀为 [BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为 0。

          |
BBC ABCDAB ABCDABCDABDE
    ABCDABD
          |

BBC ABCDAB ABCDABCDABDE
        --
    ABCDABD
    --

KMP算法详解 | Matrix67: The Aha Moments @
```
i = 1 2 3 4 5 6 7 8 9 ……
A = a b a b a b a a b a b …
B = a b a b a c b
j = 1 2 3 4 5 6 7
              ^

i = 1 2 3 4 5 6 7 8 9 ……
A = a b a b a b a a b a b …
B =     a b a b a c b
j =     1 2 3 4 5 6 7
```
预处理不需要按照 P 的定义写成 O(m^2) 甚至 O(m^3) 的。我们可以通过 P, P, …, P[j-1] 的值来获得 P[j] 的值。对于刚才的 B="ababacb"，假如我们已经求出了 P, P, P 和 P，看看我们应该怎么求出 P 和 P。P = 2，那么 P 显然等于 P+1，因为由 P 可以知道，B[1,2] 已经和 B[3,4] 相等了，现在又有 B=B，所以 P 可以由 P 后面加一个字符得到。P 也等于 P+1 吗？显然不是，因为 B[ P+1 ] != B。那么，我们要考虑“退一步”了。我们考虑 P 是否有可能由 P 的情况所包含的子串得到，即是否 P=P[ P ]+1。这里想不通的话可以仔细看一下：
```
    1 2 3 4 5 6 7
B = a b a b a c b
P = 0 0 1 2 3 ?
```
P=3 是因为 B[1..3] 和 B[3..5] 都是 “aba”；而 P=1 则告诉我们，B、B 和 B 都是“a”。既然 P 不能由 P 得到，或许可以由 P 得到（如果 B 恰好和 B 相等的话，P 就等于 P+1 了）。显然，P 也不能通过 P 得到，因为 B != B。事实上，这样一直推到 P 也不行，最后，我们得到，P=0。

怎么这个预处理过程跟前面的 KMP 主程序这么像呢？其实， KMP 的预处理本身就是一个 B 串“自我匹配”的过程。它的代码和上面的代码神似：
```
P:=0;
j:=0;
for i:=2 to m do
begin
   while (j>0) and (B[j+1]<>B[i]) do j:=P[j];
   if B[j+1]=B[i] then j:=j+1;
   P[i]:=j;
end;
```
Knuth-Morris-Pratt Algorithm
从头到尾彻底理解KMP（2014年8月22日版） - 结构之法算法之道 - 博客频道 - CSDN.NET

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

void compute_prefix(const char *pattern, int next[]) {
    int i;
    int j = -1;
    const int m = strlen(pattern);

    next = j;
    for ( i = 1; i < m; i++ ) {
        while (j > -1 && pattern[j + 1] != pattern[i]) { j = next[j]; }
        if( pattern[i] == pattern[j + 1] ) { j++; }
        next[i] = j;
    }
}

int kmp(const char *text, const char *pattern) {
    int i;
    int j = -1;
    const int n = strlen(text);
    const int m = strlen(pattern);
    if (n == 0 && m == 0) return 0; /* "","" */
    if (m == 0) return 0;  /* "a","" */
    int *next = (int*)malloc(sizeof(int) * m);

    compute_prefix(pattern, next);

    for (i = 0; i < n; i++) {
        //              printf( "\n\n\n" );
        //              printf( "      %*si = %d\n", i, "", i );
        //              printf( "      %*s|\n", i, "");
        //              printf( "text: %s\n", text );
        //              while (j > -1 && pattern[j + 1] != text[i]) {
        //                  printf( "\nj: %d->", j );
        //                  j = next[j];
        //                  printf( "%d\n", j );
        //              }
        //              printf( "      %*s%s\n", i-j-1, "", pattern );
        //              printf( "      %*s|\n", i, "");
        //              printf( "      %*sj:%d->", i-1, "", j );

        if (text[i] == pattern[j + 1]) j++;
        if (j == m - 1) {
            free(next);
            return i-j;
        }
    }

    free(next);
    return -1;
}


int main(int argc, char *argv[]) {
    char text[] = "ABC ABCDAB ABCDABCDABDE";
    char pattern[] = "ABCDABD";
    char *ch = text;
    int i = kmp(text, pattern);

    if (i >= 0) printf("matched @: %s\n", ch + i);

    //              const char *needles[] = {
    //                  "ABCDABD",
    //                  "ABC",
    //                  "ABC"
    //              };
    //              for( int i = 0; i < sizeof(needles)/sizeof(needles); ++i ) {
    //                  const char *pattern = needles[i];
    //                  static int next;
    //                  int m = strlen( pattern );
    //                  memset( next, 0, sizeof(next) );
    //                  compute_prefix( pattern, next );
    //                  printf( "next[] for: " );
    //                  for( int i = 0; i < m; ++i ) { printf("  %c  ", pattern[i] ); }
    //                  printf( "\n" );
    //                  printf( "            " );
    //                  for( int i = 0; i < m; ++i ) { printf("%3d  ", next[i] ); }
    //                  printf( "\n" );
    //              }
    return 0;
}

void compute_prefix(const char *pattern, int next[]) {
    int i;
    int j = -1;
    const int m = strlen(pattern);

    next = j;
    for (i = 1; i < m; i++) {
        while (j > -1 && pattern[j + 1] != pattern[i]) j = next[j];

        if (pattern[i] == pattern[j + 1]) j++;
        next[i] = j;
    }
}

next[] for:   A    B    C    D    A    B    D
             -1
                  -1                                p[i=1] != p[j+1=0]
                       -1                           p[i=2] != p[j+1=0]
                            -1                      p[i=3] != p[j+1=0]
                                  0                 p[i=4] == p[j+1=0], ++j, (j=1 now)
                                       ?            p   == p, not inside while
                                       1            p[i=5] == p[j+1=1], ++j, (j=2 now)
                                            ?       p   != p, j = next[j=2] = -1
                                           -1
so:
             -1   -1   -1   -1    0    1   -1

      i = 0
      |
text: ABC ABCDAB ABCDABCDABDE
      ABCDABD
      |
     j:-1

       i = 1
       |
text: ABC ABCDAB ABCDABCDABDE
      ABCDABD
       |
      j:0

        i = 2
        |
text: ABC ABCDAB ABCDABCDABDE
      ABCDABD
        |
       j:1

         i = 3
         |
text: ABC ABCDAB ABCDABCDABDE
      ABCDABD, j: 2->-1 ("ABC" -> ["A", "AB"], ["BC", "C"])
         ABCDABD
         |
        j:-1

          i = 4
          |
text: ABC ABCDAB ABCDABCDABDE
          ABCDABD
          |
         j:-1

           i = 5
           |
text: ABC ABCDAB ABCDABCDABDE
          ABCDABD
           |
          j:0

            i = 6
            |
text: ABC ABCDAB ABCDABCDABDE
          ABCDABD
            |
           j:1

             i = 7
             |
text: ABC ABCDAB ABCDABCDABDE
          ABCDABD
             |
            j:2

              i = 8
              |
text: ABC ABCDAB ABCDABCDABDE
          ABCDABD
              |
             j:3

               i = 9
               |
text: ABC ABCDAB ABCDABCDABDE
          ABCDABD
               |
              j:4

+-----------------------------------------------------------------------+
|       while (j > -1 && pattern[j + 1] != text[i]) { j = next[j]; }    |
|       j > -1                          : may backroll                  |
|       pattern[j+1] != text[i]         : mismatch                      |
+-----------------------------------------------------------------------+
|                     0    1    2    3    4    5    6                   |
|       next[] for:   A    B    C    D    A    B    D                   |
|                    -1   -1   -1   -1    0    1   -1                   |
|                     0    0    0    0    1    2    0                   |
+-----------------------------------------------------------------------+

                i = 10
                |
text: ABC ABCDAB ABCDABCDABDE
          ABCDABD               jump:   5   ->   1
              ABCDABD           jump:   1   ->  -1
                ABCDABD
                |
               j:-1

                 i = 11
                 |
text: ABC ABCDAB ABCDABCDABDE
                 ABCDABD
                 |
                j:-1

                  i = 12
                  |
text: ABC ABCDAB ABCDABCDABDE
                 ABCDABD
                  |
                 j:0

                   i = 13
                   |
text: ABC ABCDAB ABCDABCDABDE
                 ABCDABD
                   |
                  j:1

                    i = 14
                    |
text: ABC ABCDAB ABCDABCDABDE
                 ABCDABD
                    |
                   j:2

                     i = 15
                     |
text: ABC ABCDAB ABCDABCDABDE
                 ABCDABD
                     |
                    j:3

                      i = 16
                      |
text: ABC ABCDAB ABCDABCDABDE
                 ABCDABD
                      |
                     j:4

                       i = 17
                       |
text: ABC ABCDAB ABCDABCDABDE
                 ABCDABD        jump:   5   ->   1
                     ABCDABD
                       |
                      j:1

                        i = 18
                        |
text: ABC ABCDAB ABCDABCDABDE
                     ABCDABD
                        |
                       j:2


                         i = 19
                         |
text: ABC ABCDAB ABCDABCDABDE
                     ABCDABD
                         |
                        j:3

                          i = 20
                          |
text: ABC ABCDAB ABCDABCDABDE
                     ABCDABD
                          |
                         j:4

                           i = 21
                           |
text: ABC ABCDAB ABCDABCDABDE
                     ABCDABD
                           |
                          j:5

see more?

Boyer-Moore @

推荐网上的几篇比较好的博客，“字符串匹配的 Boyer-Moore 算法”，图文并茂，非常通俗易懂，作者是阮一峰；Boyer-Moore algorithm。

有兴趣的读者还可以看原始论文。

/**
 * 本代码参考了 http://www-igm.univ-mlv.fr/~lecroq/string/node14.html
 * 精力有限的话，可以只计算坏字符的后移，好后缀的位移是可选的，因此可以删除
 * suffixes(), pre_gs() 函数
 */
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define ASIZE 256  /* ASCII字母的种类 */

/*
 * @brief 预处理，计算每个字母最靠右的位置.
 *
 * @param[in] pattern 模式串
 * @param[out] right 每个字母最靠右的位置
 * @return 无
 */
static void pre_right(const char *pattern, int right[]) {
    int i;
    const int m = strlen(pattern);

    for (i = 0; i < ASIZE; ++i) right[i] = -1;
    for (i = 0; i < m; ++i) right[(unsigned char)pattern[i]] = i;
}

static void suffixes(const char *pattern, int suff[]) {
    int f, g, i;
    const int m = strlen(pattern);

    suff[m - 1] = m;
    g = m - 1;
    for (i = m - 2; i >= 0; --i) {
        if (i > g && suff[i + m - 1 - f] < i - g)
            suff[i] = suff[i + m - 1 - f];
        else {
            if (i < g)
                g = i;
            f = i;
            while (g >= 0 && pattern[g] == pattern[g + m - 1 - f])
                --g;
            suff[i] = f - g;
        }
    }
}

/*
 * @brief 预处理，计算好后缀的后移位置.
 *
 * @param[in] pattern 模式串
 * @param[out] gs 好后缀的后移位置
 * @return 无
 */
static void pre_gs(const char pattern[], int gs[]) {
    int i, j;
    const int m = strlen(pattern);
    int *suff = (int*)malloc(sizeof(int) * (m + 1));

    suffixes(pattern, suff);

    for (i = 0; i < m; ++i) gs[i] = m;

    j = 0;
    for (i = m - 1; i >= 0; --i) if (suff[i] == i + 1)
        for (; j < m - 1 - i; ++j) if (gs[j] == m)
            gs[j] = m - 1 - i;
    for (i = 0; i <= m - 2; ++i)
        gs[m - 1 - suff[i]] = m - 1 - i;
    free(suff);
}

Rabin-Karp :TODO: @

TODO

从面试官的角度分析面试的考察点 @
- 如果没有 strlen？要自己写一个？还是融汇在的自己代码里。
- 输入参数上，char *str 改成 const char *str 是不是更好？
- 参数命名上，str 和 sub 好不好？要不换成 haystack 和 needle 怎么样？
- int len = strlen(str) 这里 len 的类型换成 size_t 是不是更好？ int 型最多表示多长的字节？ 2³¹-1 / 2¹⁰ (k) / 2¹⁰ (m) / 2¹⁰ (g) = 2^31-30 = 2 GB。我猜完全没有必要用……
上面的问题你怎么回答。
从 Subset 中了解算法面试中模板的重要性 @

挺重要。

同样动作重复 300 次，肌肉就会有记忆，而一个动作重复 600 次，脊椎就会有记忆。

— 李小龙

程序设计入门建议 @

我们的目标是解决问题，而不是为了写程序而写程序，同时应保持简单（Keep It Simple and Stupid, KISS），而不是自己创造条件去展示编程技巧。

三整数排序

#include <stdio.h>

int main() {
    int a, b, c, t;
    scanf( "%d%d%d", &a, &b, &c );
    if( a > b ) { t = a; a = b; b = t; } // a <= b
    if( a > c ) { t = a; a = c; c = t; } // a <= c
    if( b > c ) { t = b; b = c; c = t; } // a <= b <= c
    printf( "%d %d %d\n", a, b, c );
    return 0;
}

step by step, get closer to your goal.

重定向（便于本地测试） ♥️

freopen( "data.in",  "r", stdin  );
freopen( "data.out", "w", stdout );

编程不是看书看会的，也不是听课听会的，而是练会的。

refs and see also

程序员编程艺术：第四章、现场编写类似 strstr/strcpy/strpbrk 的函数 - 结构之法算法之道 - 博客频道 - CSDN.NET

✂️ 2016/00/00 上午 9:30:00 0. 编程初步以及 STL 入门 @

第 3 章，数组和字符串 @

蛇形填数 @

#include <stdio.h>
#include <string.h>
#define maxn 20
int a[maxn][maxn];

int main() {
    int n, x, y, tot = 0;
    while( 1 == scanf( "%d", &n ) && n > 0 && n < maxn ) {
        memset( a, 0, sizeof(a) );
        tot = a[x=0][y=n-1] = 1;
        while( tot < n*n ) {
            while( x+1 <  n && !a[x+1][y] ) { a[++x][y] = ++tot; }
            while( y-1 >= 0 && !a[x][y-1] ) { a[x][--y] = ++tot; }
            while( x-1 >= 0 && !a[x-1][y] ) { a[--x][y] = ++tot; }
            while( y+1 <  n && !a[x][y+1] ) { a[x][++y] = ++tot; }
        }
        for( x = 0; x < n; ++x ) {
            for( y = 0; y < n; ++y ) {
                printf( "%5d", a[x][y] );
            }
            printf( "\n" );
        }
    }
    return 0;
}

最好在做一件事之前检查是不是可以做，而不要做完再后悔。因为“毁棋”往往比较麻烦。

if( strchr( s, c ) == NULL ) { ... }

int idx = strchr(s, c) - s;
if( s[idx] ) {
    ...
}

fgetc 返回 int？因为 EOF（值为 -1）不容易转化成 char。

回文词（Palindromes） @

输入中没有 “0”。

#include <stdio.h>
#include <string.h>
#include <ctype.h>
//                 ABCDEFGHIJKLMNOPQRSTUVWXYZ123456789
const char *rev = "A   3  HIL JM O   2TUVWXY51SE Z  8 ";
const char *msg[] = {   "not a palindrome",
                        "a regular palindrome",
                        "a mirrored string",
                        "a mirrored palindrome" };

char r( char ch ) {
    if( isupper(ch) ) {
        return rev[ch-'A'];
    } else if( '0' < ch && ch <= '9' ) {
        return rev[ch-'1'+26];
    } else {
        return 0; // then should not equal
    }
}

int main() {
    char s;
    while( scanf( "%s", s ) == 1 ) {
        int len = strlen(s);
        int p = 1, m = 1;
        // 不是 len/2，你说为什么呢？ because:          s[i] === s[i] but, s[i] !== rev(s[i]), not always
        for( int i = 0; i < (len+1)/2; ++i ) {
            if(   s[i]  != s[len-1-i] ) { p = 0; }
            if( r(s[i]) != s[len-1-i] ) { m = 0; }
            if( !p && !m ) { break; }
        }
        printf( "%s -- is %s.\n\n", s, msg[m*2+p] );
    }
    return 0;
}

编译运行：

$ gcc palindromes.c -o palindromes -std=c99

$ cat input.txt
NOTAPALINDROME
ISAPALINILAPASI
2A3MEAS
ATOYOTA

$ cat input.txt | palindromes
NOTAPALINDROME -- is not a palindrome.

ISAPALINILAPASI -- is a regular palindrome.

2A3MEAS -- is a mirrored string.

ATOYOTA -- is a mirrored palindrome.

环状序列（Circular Sequence） @

+--------->---------+
|  T  C    G       \|/
|              A    |
| C               G |
^                   |
| G               T |
|     G    A  C     |
+-----<----^--------+
            \
             +----- 最小从这里开始

#include <stdio.h>
#include <string.h>
#define maxn 105

int less( const char *s, int p, int q ) {
    int n = strlen(s);
    for( int i = 0; i < n; ++i ) {
        if( s[(p+i)%n] != s[(q+i)%n] ) {
            return s[(p+i)%n] < s[(q+i)%n];
        }
    }
    return 0; // equal
}

int main() {
    char s[maxn];
    while( 1 == scanf( "%s", s ) ) {
        int ans = 0;
        int n = strlen(s);
        for( int i = 1; i < n; ++i ) {
            if( less(s, i, ans) ) { ans = i; }
        }
        printf( "%s --> \"", s );
        for( int i = 0; i < n; ++i ) {
            putchar( s[(i+ans)%n] );
        }
        printf( "\"\n" );
    }
    return 0;
}

猜数字 😞 @

输入：

4                           # 对于一个 case，4 表示每行四个数字
1   3   5   5               # 猜测的数字
1   1   2   3               # 正确的数字
4   3   3   5               # 猜测
6   5   5   1               # 正确
6   1   3   5
1   3   5   5
0   0   0   0               # 全 0，结束
0                           # 0，表示所有输入结束

统计输出有多少数字位置正确（A），多少数字在两个序列多出现了但位置不对（B）。

分析：

统计可以得到 A。对 1~9，统计两者出现的次数 c1 和 c2，则 min( c1, c2 ) 就是该数字对 B 的贡献（最后要减去 A 的部分）。

#include<stdio.h>
#define maxn 1000 + 10

int main() {
    int n, a[maxn], b[maxn];
    int kase = 0;
    while( scanf("%d", &n) == 1 && n ) {            // n=0 时输入结束
        printf( "Game %d:\n", ++kase );
        for( int i = 0; i < n; i++ ) { scanf("%d", &a[i]); }
        for( ; ; ) {
            int A = 0, B = 0;
            for( int i = 0; i < n; i++ ) {
                scanf( "%d", &b[i] );
                if( a[i] == b[i] ) { A++; }         // 统计 A
            }
            if( b == 0 ) { break; }                 // 正常的猜测序列不会有 0，所以只判断第一个数是否为 0 即可
            for(int d = 1; d <= 9; d++) {
                int c1 = 0, c2 = 0;                 // 统计数字 d 在答案序列和猜测序列中各出现多少次
                for(int i = 0; i < n; i++) {
                    if(a[i] == d) c1++;
                    if(b[i] == d) c2++;
                }
                B += c1 < c2 ? c1 : c2;
            }
            printf("    (%d,%d)\n", A, B-A);
        }
    }
    return 0;
}

生成元 😞 @
x 加上 x 的各个数字得到 y，就说 x 是 y 的生成元。给出 n （1<=n<=100000），求最小生成元。无解输出 0。例如，n=216，121，2005 时的解围 198，0， 1979。
```
#include<stdio.h>
#include<string.h>
#define maxn 100005
int ans[maxn];

int main() {
  int T, n;
  memset(ans, 0, sizeof(ans));
  for(int m = 1; m < maxn; m++) {
    int x = m, y = m;
    while(x > 0) { y += x % 10; x /= 10; }
    if(ans[y] == 0 || m < ans[y]) ans[y] = m;
  }
  scanf("%d", &T);
  while(T--) {
    scanf("%d", &n);
    printf("%d\n", ans[n]);
  }
  return 0;
}
```
我的分析：一个五位数（最多），最多能添加 9x5，所以要求 y 的生成元，只要在 [y-9*5, y) 枚举就可以了。书中给的代码适合本来就有很多数字需要判断，我的适合于只有一两个数字需要判断。代码就不贴了（因为很简单）。

第 4 章，函数和递归 @

知识点 ♥️ @
- 由于使用了调用栈，C 语言自然支持了递归。在 C 语言中，调用自己和调用其他函数并没有本质不同。
- 正文段（Text Segment）存储指令，数据段（Data Segment）用于存储已经初始化的全局变量； BSS 段（BSS Segment）用于存储没赋值的全局变量所需的空间。运行时创建的调用栈所在段区被称为堆栈段（Stack Segment），越界访问就会出现 Segment Fault。栈帧太多，可能越界，这叫栈溢出（Stack Overflow）。
  
  可以用 ulimit -a 显示 stack size，用 ulimit -s 32768 设置为 32 MB。 Windows 上也可以设置。
  
  局部变量太大，也可能 stack overflow。

古老的密码 😞 @

一个随意的字符串 JWPUDJSTVP 能不能通过字符变换变成 VICTORIOUS，只要统计单词的频率，看是否匹配就可以了。

#include <stdio.h>
#include <string.h>                                             // strlen
#include <stdlib.h>                                             // qsort

#define ASCIISZIE 128

int cmp( const void *a, const void *b ) {
    return *(int *)a - *(int *)b;
}

int main() {
    char s1, s2;
    while( scanf( "%s%s", s1, s2 ) == 2 ) {
        int n = strlen(s1);
        // assert( strlen(s1) == strlen(s2) );
        int cnt1[ASCIISIZE] = {0}, cnt2[ASCIISIZE] = {0};
        for( int i = 0; i < n; i++ ) { cnt1[s1[i] - 'A']++; }   // 统计
        for( int i = 0; i < n; i++ ) { cnt2[s2[i] - 'A']++; }
        qsort( cnt1, ASCIISIZE, sizeof( int ), cmp );           // 对字频排序
        qsort( cnt2, ASCIISIZE, sizeof( int ), cmp );
        int ok = 1;
        for( int i = 0; i < ASCIISIZE; i++ ) {
            if( cnt1[i] != cnt2[i] ) { ok = 0; }                // 是否匹配？
        }
        if( ok ) {
            printf( "YES\n" );
        } else {
            printf( "NO\n" );
        }
    }
    return 0;
}

也可以用 c++ 的 sort，修改如下几行即可：

#include<algorithm>                                             // sort
sort( cnt1, cnt1 + 26 );
sort( cnt2, cnt2 + 26 );

骰子涂色 ♥️ @

rbgggr 和 rggbgr 一样。

            +-------------+
           /             /|  +------------5
          /      1      / | /
         /             /  |/
        +------------+/   |
3 ----> |            |    |
        |            | 4  /
        |     2      |   /
        |            |  /
        |            | /
        +------------+/
              ^
              |
              +-- 6

天平 ♥️ @

input:

#include <iostream>
using namespace std;

bool solve( int &W ) {
    int W1, D1, W2, D2;
    bool b1 = true, b2 = true;
    cin >> W1 >> D1 >> W2 >> D2;
    if( !W1 ) { b1 = solve( W1 ); }
    if( !W2 ) { b2 = solve( W2 ); }
    W = W1 + W2;
    return b1 && b2 && ( W1*D1 == W2*D2 );
}

int main() {
    int T, W;
    cin >> T;
    while( T-- ) {
        if( solve(W) ) {
            cout << "YES\n";
        } else {
            cout << "No\n";
        }
        if( T ) { cout << "\n"; }
    }
    return 0;
}

第 5 章，C++ 与 STL 入门 @

5.1 From C to C++ @

template, reference, containers, iostream, operators, etc

template<typename T>
T sum( T *begin, T *end ) {
    T ans = 0;
    for( T *p = begin; p != end; ++p ) {
        ans = ans + *p;
    }
    return ans;
}

see tutorial: C/C++ notes.

5.2 STL 101 @

大理石在哪儿？ sort, lower_bound @

input:

    4   1
    2   3   5   1
    5
    5   2
    1   3   3   3   1

output:

    CASE# 1:
    5 found at 4
    CASE# 2:
    2 not found
    3 found at 3

#include <stdio.h>
#include <algorithm>
using namespace std;

const int maxn = 10000;

int main() {
    int n, q, x a[maxn], kase = 0;
    while( scanf( "%d%d", &n, &q ) == 2 && n ) {
        printf( "CASE# %d:\n", ++kase );
        for( int i = 0; i < n; ++i ) { scanf( "%d", &a[i] ); }
        sort( a, a+n );
        while( q-- ) {
            scanf( "%d", &x );
            int p = lower_bound( a, a+n, x ) - a;       // offset
            if( a[p] == x ) {
                printf( "%d found at %d\n", x, p+1 );
            } else {
                printf( "%d not found\n", x );
            }
        }
    }
    return 0;
}

run it:

$ echo "4 1\n2 3 5 1\n5" | ./a.out
CASE# 1:
5 found at 4

Set, Map set<int>::iterator @

elements in set already sorted.

int main() {
    string s, buf;
    set<string> dict;
    while( cin >> s ) {
        for( int i = 0; i < s.length(); ++i ) {
            if( isalpha(s[i]) ) {
                s[i] = tolower(s[i]);
            } else {
                s[i] = ' ';
            }
        }
        stringstream ss( s );
        while( ss >> buf ) {
            dict.insert( buf );                                                         // set.insert( item )
        }
        for( set<string>::iterator it = dict.begin(); it != dict.end(); ++it ) {        // 迭代器输出所有元素
            cout << *it << "\n";                                                        // already sorted
        }
    }
    return 0;
}

map

string repr( const string &s ) {                    // signature
    string ans = s;
    for( int i = 0; i < ans.length(); ++i ) {
        ans[i] = tolower(ans[i]);
    }
    sort( ans.begin(), ans.end() );
    return ans;
}

int main() {
    ...
    while( cin >> s ) {
        string r = repr( s );
        if( !cnt.count(r) ) { cnt[r] = 0; }         // this is optional
        ++cnt[r];
    }
    vector<string> ans;
    for( int i = 0; i < words.size(); ++i ) {
        if( cnt[repr(words[i])] == 1 ) {
            ans.push_back( words[i] );
        }
    }
    sort( ans.begin(), ans.end() );
    for( int i = 0; i < ans.size(); ++i ) {
        coutt << ans[i] << "\n";
    }

    return 0;
}

需要注意的是：

直接用 ++cnt[r] 也是可以的；
map.count( key ) 返回 1 或者 0；
map.find( key ) 返回 iter，可能是 map.end()

Stack, Queue, Priority Queue @

stack @

明白 stack，以及常用的 push(item), item = top(), pop() 操作。

//  print stack contents
for( std::stack<int> dump = stack; !dump.empty(); dump.pop() ) {
    std::cout << dump.top() << '\n';
}

The SetStack Computer，支持如下操作：

PUSH：空集“{}”入栈
DUP：复制栈顶并入栈
UNION：出栈两个元素，求 union 并入栈
INTERSECT：出栈两个元素，求 intersect 并入栈
ADD：出栈两个元素，把先出的元素加到后出的元素，然后入栈

集合的集合的表示？

一个集合有整形的 id，它的内容用 set<int> 表示。整个栈用 stack<int> 表示。

// UVa12096 The SetStack Computer
#include <iostream>
#include <string>
#include <set>
#include <map>
#include <stack>
#include <vector>
#include <algorithm>
using namespace std;

#define ALL(x) x.begin(), x.end()
#define INS(x) inserter(x, x.begin())

typedef set<int> Set;
map<Set,int> IDcache;                                       // 把集合映射成 ID
vector<Set> Setcache;                                       // 根据 ID 取集合

// 查找给定集合 x 的 ID。如果找不到，分配一个新 ID
int ID( Set x ) {
    if( IDcache.count( x ) ) { return IDcache[x]; }
    Setcache.push_back( x );                                // 添加新集合
    return IDcache[x] = Setcache.size() - 1;
}

int main () {
    int T;
    cin >> T;
    while( T-- ) {
        stack<int> s;                                       // 题目中的栈
        int n;
        cin >> n;
        for( int i = 0; i < n; i++ ) {
            string op;
            cin >> op;
            if( op == 'P' ) {
                s.push( ID( Set() ) );                      // push '{}'
            } else if( op == 'D' ) {
                s.push( s.top(  ) );                        // dup
            } else {
                Set x1 = Setcache[s.top()]; s.pop();
                Set x2 = Setcache[s.top()]; s.pop();
                Set x;
                if( op == 'U' ) { set_union ( ALL( x1 ), ALL( x2 ), INS( x ) ); }
                if( op == 'I' ) { set_intersection ( ALL( x1 ), ALL( x2 ), INS( x ) ); }
                if( op == 'A' ) { x = x2; x.insert( ID( x1 ) ); }
                s.push(ID(x));
            }
            cout << Setcache[s.top()].size() << endl;
        }
        cout << "***" << endl;
    }
    return 0;
}

queue @

cpp queue<int> q; q.push( val ); q.pop(); q.front(); q.back();

t 个队伍排队。新来的人，如果有队友，就插入到队友后面，如果没有，就只能排最后面。输入每个团队中所有队员的编号，要求支持如下 3 中命令：

ENQUEUE x：把 x 入队
DEQUEUE
STOP：停止模拟

对于每个 DEQUEUE 指令，输出出对的人的编号。

// UVa540 Team Queue
#include <cstdio>
#include <queue>
#include <map>
using namespace std;

const int maxt = 1000 + 10;

int main() {
    int t, kase = 0;
    while( scanf( "%d", &t ) == 1 && t ) {
        printf( "Scenario #%d\n", ++kase );

        map<int, int> team;                                     // team[x] 表示编号为 x 的人所在的团队编号
        for( int i = 0; i < t; i++ ) {
            int n, x;
            scanf( "%d", &n );
            while( n-- ) { scanf( "%d", &x ); team[x] = i; }
        }

        // 模拟
        queue<int> q, q2[maxt];                                 // q 是团队的队列，而 q2[i] 是团队 i 成员的队列

        for( ;; ) {
            int x;
            char cmd;
            scanf( "%s", cmd );
            if( cmd == 'S' ) { break; }
            else if( cmd == 'D' ) {
                int t = q.front();
                printf( "%d\n", q2[t].front() ); q2[t].pop(  );
                if( q2[t].empty(  ) ) { q.pop(); }              // 团体 t 全体出队列
            }
            else if( cmd == 'E' ) {
                scanf( "%d", &x );
                int t = team[x];
                if( q2[t].empty() ) q.push( t );                // 团队 t 进入队列
                q2[t].push( x );
            }
        }
        printf( "\n" );
    }

    return 0;
}

priority_queue ♥️ @

cpp pq.push(); pq.top(); pq.pop();

ugly number 是不能被 2，3，5 以为的其他素数整除的数。（相比质数不是那么严格。）也就是 2，3，5 的各种）乘积的组合。

如果 x 是 ugly number，2x，3x 和 5x 都会是 ugly number。用优先队列即可。

#include <iostream>
#include <vector>
#include <queue>
#include <set>

using namespace std;
typedef long long LL;

int main() {
    int n;
    while( scanf("%d", &n) && n ) {
        priority_queue<LL, vector<LL>, greater<LL> > pq;                            // greater 于是 ascend 排序
        pq.push( 1LL );
        set<LL> s;
        s.insert( 1LL );

        for( int i = 1; ; ++i ) {
            LL x = pq.top(); pq.pop();  // the smallest ugly number
            if( i == n ) {
                cout << "The " << n << "'th ugly number is " << x << ".\n";
                int j = 0;
                for( set<LL>::iterator it = s.begin(); it != s.end(); ++it ) {
                    if( ++j == n ) {
                        cout << "The " << n << "'th ugly number is " << *it << ".\n";
                    }
                }
                break;
            }
            for( int j = 0; j < 3; ++j ) {
                const int coeff = {  2,  3,  5   };
                LL x2 = x * coeff[j];
                if( !s.count(x2) ) {
                    s.insert( x2 );
                    pq.push( x2 );
                }
            }
        }
    }
}

output:

$ a.out
1500<RET>
The 1500'th ugly number is 859963392.
The 1500'th ugly number is 859963392.

从队列前面取出的第 n 个数正好是第 n 个大的 ugly number。

注：

priority_queue<int> pq 是越小的整数优先级越低（逆序）
priority_queue<int, vector<int>, greater<int> > pq 是越大的整数优先级越低（正序）
queue 使用 front()，priority queue 使用 top()

Test STL @
tips and guidelines
- RAND_MAX may be only 32767 (2¹⁵-1)
- use assert( ... ), header file is <assert.h>
- vector, set, map are fast.

5.3 Big Integer @

bool operator >  ( const T &rhs ) const { return   rhs < *this;     }
bool operator <= ( const T &rhs ) const { return !(rhs < *this);    }
bool operator != ( const T &rhs ) const { return !(*this == rhs);   }

在 32 位 CPU 下，C/C++ 中的 int 能表示的范围是 -2³¹ ~ 2³²-1， unsigned int 能表示的范围是 0 ~ 2³²。所以，int 和 unsigned int 都不能保存超过 10 位的整数 (解方程 10^x <= 2³²，可得 x <= 9.63。) 有时我们需要参与运算的整数，可能会远远不止 10 位，我们称这种基本数据类型无法表示的整数为大整数。如何表示和存放大整数呢？基本的思想是：用数组模拟大整数。一个数组元素，存放大整数中的一位。

例如，一个 200 位的十进制整数，可以用 int x[200] 来表示，一个数组元素对应一个位。这样做有点浪费空间，因为一个 int 可以表示的范围远远大于 10。因此，我们可以用一个数组元素，表示 4 个数位（一个 int 可以表示的范围也远远大于 10000，为什么一个数组元素只表示 4 个数位，可不可以表示 9 个数位？留给读者思考），这时，数组不再是 10 进制，而是 10000 进制。使用万进制，数组长度可以缩减到原来的 1/4。

(我觉得, 万进制方便实现乘法, 不容易越界.)

大整数加法 @

求两个非负的大整数相加的和。

输入

    有两行，每行是一个不超过 200 位的非负整数，可能有多余的前导 0。

    33333333333333333333
    22222222222222222222

    234123412341324190834500091234087501234087
    190834500091234087501234087412340871234609

    234123412341324190834500091234087501234087234444444444444444444444
    12134123442134190834500091234087501234087412340871234609

    999999999999999
    5

    999999999999999999999999999999999999999999999999999999999999999999
    1

输出

    一行，即相加后的结果。结果里不能有多余的前导 0，即如果结果是 342，那么就不
    能输出为 0342。

    33333333333333333333 +
    22222222222222222222 =
    55555555555555555555

    234123412341324190834500091234087501234087 +
    190834500091234087501234087412340871234609 =
    424957912432558278335734178646428372468696

    234123412341324190834500091234087501234087234444444444444444444444 +
    12134123442134190834500091234087501234087412340871234609 =
    234123412353458314276634282068587592468174735678531856785315679053

    999999999999999 +
    5 =
    1000000000000004

    999999999999999999999999999999999999999999999999999999999999999999 +
    1 =
    1000000000000000000000000000000000000000000000000000000000000000000

#include <stdio.h>
#include <string.h>
#include <stdlib.h>

// 一个数组元素表示 4 个十进制位，即数组是万进制的
#define BIGINT_RADIX 10000
#define RADIX_LEN 4
#define MAX_LEN (200/RADIX_LEN+1)                               // 整数的最大位数

char a[MAX_LEN * RADIX_LEN], b[MAX_LEN * RADIX_LEN];
int  x[MAX_LEN], y[MAX_LEN];
int  z[MAX_LEN * 2]; // bigint_mul

void bigint_print( const int x[], const int n ) {
    bool start_output = false;              // 用于跳过前导 0
    for( int i = n - 1; i >= 0; --i ) {
        if( start_output ) {                // 如果多余的 0 已经都跳过，则输出
            printf( "%04d", x[i] );
            continue;
        }
        if( x[i] > 0 ) {
            printf( "%d", x[i] );           // 本题输出比较坑爹，最高位数字有前导 0
            start_output = true;            // 碰到第一个非 0 的值，就说明多余的 0 已经都跳过
        }
    }

    if ( !start_output ) { printf("0"); }   // 当 x 全为 0 时
}

// x 大整数，用数组表示，低位在低地址
void bigint_input( const char s[], int x[] ) {
    // memset( x, 0, sizeof(x) ); sizeof(x) == sizeof(int *)
    memset( x, 0, MAX_LEN*sizeof(int) );
    int j = 0;
    for( int i = strlen(s); i > 0; i -= RADIX_LEN ) {  /* [i-RADIX_LEN, i) */
        int low = i-RADIX_LEN > 0 ? i-RADIX_LEN : 0;
        int temp = 0;
        for( int k = low; k < i; ++k ) {
            temp = temp * 10 + s[k] - '0';
        }
        x[j++] = temp;
    }
}

void bigint_add( const int x[], const int y[], int z[] ) {
    memset( z, 0, (MAX_LEN*2)*sizeof(int) );
    for( int i = 0; i < MAX_LEN; ++i ) {
        z[i] += x[i] + y[i];
        if( z[i  ] >= BIGINT_RADIX ) {
            z[i+1] += z[i] / BIGINT_RADIX;
            z[i  ] %= BIGINT_RADIX;
        }
    }
}

int main() {
    while( 2 == scanf( "%s %s", a, b ) ) {
        bigint_input( a, x );
        bigint_input( b, y );
        bigint_add( x, y, z );
        bigint_print( x, sizeof(x)/sizeof(x[0]) ); printf(" + \n");
        bigint_print( y, sizeof(y)/sizeof(y[0]) ); printf(" = \n");
        bigint_print( z, sizeof(z)/sizeof(z[0]) ); printf("\n\n");
    }
    return 0;
}

## more about bigint input

void bigint_input( const char s[], int x[] ) {  // x 大整数，用数组表示，低位在低地址
    // don't not use 'memset( x, 0, sizeof(x) );' because 'sizeof(x) == sizeof(int *)'
    memset( x, 0, MAX_LEN*sizeof(int) );
    int j = 0;
    for( int i = strlen(s); i > 0; i -= RADIX_LEN ) {
        // (i, i-RADIX_LEN]
        int low = i-RADIX_LEN > 0 ? i-RADIX_LEN : 0;
        int temp = 0;
        printf( "s[%d, %d) = \"", low, i );
        for( int k = low; k < i; ++k ) {
            temp = temp * 10 + s[k] - '0';
            printf( "%c", s[k] );
        }
        printf( "\", \t\t" ); printf( "x[j=%d] = %d\n", j, temp );
        x[j++] = temp;
    }
}

111222333444555666777888999

111
  2223
      3344
          4555
               6667
                   7788
                       8999

                       8        = 0*10      +   [8]
                       89       = 8*10      +   [9]
                       899      = 89*10     +   [9]
                       8999     = 899*10    +   [9]

s[23, 27) = "8999",         x[j=0] = 8999
s[19, 23) = "7788",         x[j=1] = 7788
s[15, 19) = "6667",         x[j=2] = 6667
s[11, 15) = "4555",         x[j=3] = 4555
s[ 7, 11) = "3344",         x[j=4] = 3344
s[ 3,  7) = "2223",         x[j=5] = 2223
s[ 0,  3) =  "111",         x[j=6] =  111

大整数减法 @

void bigint_sub( const int x[], const int y[], int z[] ) {
    memset( z, 0, (MAX_LEN*2)*sizeof(int) );
    for( int i = 0; i < MAX_LEN; ++i ) {
        z[i] += x[i] - y[i];
        while( z[i] < 0 ) {                  // 看是否要借位
            z[i] += BIGINT_RADIX;
            --z[i+1];
        }
    }
}

33333333333333333333 -
22222222222222222222 =
11111111111111111111

234123412341324190834500091234087501234087 -
190834500091234087501234087412340871234609 =
43288912250090103333266003821746629999478

234123412341324190834500091234087501234087234444444444444444444444 -
12134123442134190834500091234087501234087412340871234609 =
234123412329190067392365900399587409999999733210357032103573209835

999999999999999 -
5 =
999999999999994

999999999999999999999999999999999999999999999999999999999999999999 -
1 =
999999999999999999999999999999999999999999999999999999999999999998

大整数乘法 @

两个 200 位的数相乘，积最多会有 400 位。

计算的过程基本上和小学生列竖式做乘法相同。为编程方便，并不急于处理进位，而将进位问题留待最后统一处理。

一个数的第 i 位和另一个数的第 j 位相乘所得的数，一定是要累加到结果的第 i+j 位上。这里 i, j 都是从右往左，从 0 开始数。

void bigint_mul( const int x[], const int y[], int z[] ) {
    memset( z, 0, (MAX_LEN*2)*sizeof(int) );
    for( int i = 0; i < MAX_LEN; ++i ) {
        for( int j = 0; j < MAX_LEN; ++j ) {
            z[i + j] += y[i] * x[j];                    // 两数第 i, j 位相乘，累加到结果的第 i+j 位
            if( z[i + j] >= BIGINT_RADIX ) {            // 看是否要进位
                z[i+j+1] += z[i + j] / BIGINT_RADIX;
                z[i + j] %= BIGINT_RADIX;
            }
        }
    }
}

33333333333333333333 x
22222222222222222222 =
740740740740740740725925925925925925926

234123412341324190834500091234087501234087 x
190834500091234087501234087412340871234609 =
44678824353810467183442287509177670164600699173891564239282307776984043046804916983

234123412341324190834500091234087501234087234444444444444444444444 x
12134123442134190834500091234087501234087412340871234609 =
2840882386043311185404680351433686312716618743780815470159469535469124552403228890832162235291280220562627816737390562396

999999999999999 x
5 =
4999999999999995

999999999999999999999999999999999999999999999999999999999999999999 x
1 =
999999999999999999999999999999999999999999999999999999999999999999

大整数乘法 @

基本的思想是反复做减法，看看从被除数里最多能减去多少个除数，商就是多少。一个一个减显然太慢，如何减得更快一些呢？以 7546 除以 23 为例来看一下：开始商为 0。先减去 23 的 100 倍，就是 2300，发现够减 3 次，余下 646。于是商的值就增加 300。然后用 646 减去 230，发现够减 2 次，余下 186，于是商的值增加 20。最后用 186 减去 23，够减8 次，因此最终商就是 328。

所以本题的核心是要写一个大整数的减法函数，然后反复调用该函数进行减法操作。

计算除数的 10 倍、100 倍的时候，不用做乘法，直接在除数后面补 0 即可。

int length( const int x[] ) {
    int result = 0;
    for( int i = MAX_LEN - 1; i >= 0; --i ) {
        if( x[i] > 0 ) { result = i + 1; break; }
    }
    return result;
}
int helper_sub( int x[], const int y[] ) {
    int lenx = length(x);
    int leny = length(y);
    // 判断 x 是否比 y 大
    if( lenx < leny ) { return -1; }
    if( lenx == leny ) {
        int larger = 0;
        for( int i = lenx - 1; i >= 0; --i ) {
            if( x[i] > y[i] ) {
                larger = 1;
            } else if ( x[i] < y[i] ) {
                if( !larger ) { return -1; }
            }
        }
    }

    for( int i = 0; i < MAX_LEN; ++i ) {    // 逐位相减
        x[i] -= y[i];
        while( x[i] < 0 ) {                 // 看是否要借位
            x[i] += BIGINT_RADIX;
            x[i+1] --;
        }
    }
    return 1;
}

void bigint_div( int x[], const int y[], int z[] ) {
    int xlen = length(x);
    int ylen = length(y);
    int times = xlen - ylen;

    memset( z, 0, (MAX_LEN*2)*sizeof(int) );

    if( times < 0 ) { return; }                     // z = 0

    int *yy = (int *)malloc(sizeof(int) * MAX_LEN); // y 的副本
    memcpy( yy, y, sizeof(int) * MAX_LEN );

    // 将 yy 右移 times 位，使其长度和 x 相同，即 yy 乘以 10000 的 times 次幂
    for( int i = xlen - 1; i >= 0; --i ) {
        if( i >= times ) {
            yy[i] = yy[i - times];
        } else {
            yy[i] = 0;
        }
    }

    // 先减去若干个 y×(10000 的 times 次方)，不够减了，再减去若干个 y×(10000 的
    // times-1 次方) 一直减到不够减为止
    ylen = xlen;
    for( int i = 0; i <= times; ++i ) {
        while( helper_sub( x, yy) >= 0 ) {
            ++z[times - i];
        }
        // yy 除以BIGINT_RADIX，即左移一位
        for( int j = 1; j < ylen; ++j ) {
            yy[j - 1] = yy[j];
        }
        yy[--ylen] = 0;
    }
    free( yy );

    // 下面的循环统一处理进位
    for( int i = 0; i < MAX_LEN - 1; ++i ) {
        if( z[i  ] >= BIGINT_RADIX ) {          // 看是否要进位
            z[i+1] += z[i] / BIGINT_RADIX;      // 进位
            z[i  ] %= BIGINT_RADIX;
        }
    }
}

$ cat input.txt
33333333333333333333
22222222222222222222

234123412341324190834500091234087501234087
190834500091234087501234087412340871234609

234123412341324190834500091234087501234087234444444444444444444444
12134123442134190834500091234087501234087412340871234609

999999999999999
5

999999999999999999999999999999999999999999999999999999999999999999
1

12345678900
98765432100

2405337312963373359009260457742057439230496493930355595797660791082739646
2987192585318701752584429931160870372907079248971095012509790550883793197894

10000000000000000000000000000000000000000
10000000000

5409656775097850895687056798068970934546546575676768678435435345
1

2405337312963373359009260457742057439230496493930355595797660791082739646
2987192585318701752584429931160870372907079248971095012509790550883793197894

10000000000000000000000000000000000000000
10000000000

5409656775097850895687056798068970934546546575676768678435435345
1

$ cat input.txt | ./a.out
33333333333333333333 /
22222222222222222222 =
1

234123412341324190834500091234087501234087 /
190834500091234087501234087412340871234609 =
1

234123412341324190834500091234087501234087234444444444444444444444 /
12134123442134190834500091234087501234087412340871234609 =
19294629188

999999999999999 /
5 =
199999999999999

999999999999999999999999999999999999999999999999999999999999999999 /
1 =
999999999999999999999999999999999999999999999999999999999999999999

12345678900 /
98765432100 =
0

2405337312963373359009260457742057439230496493930355595797660791082739646 /
2987192585318701752584429931160870372907079248971095012509790550883793197894 =
0

10000000000000000000000000000000000000000 /
10000000000 =
1000000000000000000000000000000

5409656775097850895687056798068970934546546575676768678435435345 /
1 =
5409656775097850895687056798068970934546546575676768678435435345

2405337312963373359009260457742057439230496493930355595797660791082739646 /
2987192585318701752584429931160870372907079248971095012509790550883793197894 =
0

10000000000000000000000000000000000000000 /
10000000000 =
1000000000000000000000000000000

5409656775097850895687056798068970934546546575676768678435435345 /
1 =
5409656775097850895687056798068970934546546575676768678435435345

大数阶乘 @

大数阶乘的位数 @

求 n! 的位数， 0 <= n <= 10^7。

输入

    第一行是一个正整数 T，表示测试用例的个数。接下来的 T 行，每行一个正整数 n。

    2
    10
    20

输出

    对每个 n，每行输出 n! 的位数

    7
    19

最简单的办法，是老老实实计算出 n!，然后就知道它的位数了。但这个方法很慢，会超时 (TLE)。

组合数学里有个 Stirling 公式 (Stirling’s formula)

可以用这个公式来计算 n! 的位数，它等于

                              n!
     lim        -----------------------------       =             1
                   sqrt(2*pi*n) * (n/e)^n
    n->inf


    n! 的位数          =    n * log(n/e) + 1/2 * log(2*pi*n)   +  1

        100            ->   log(100) +1 = 2+1 = 3
        1000           ->   log(1000)+1 = 3+1 = 4

#include <stdio.h>
#include <math.h>

int factorial_digits( unsigned int n ) {
    const static double PI = 3.14159265358979323846;
    const static double E = 2.7182818284590452354;
    if( n == 0 ) { return 1; }
    return 1 + (int)( n*log10(n/E) + 0.5*log10(2*PI*n) );
}

int main() {
    int T;
    while( 1 == scanf("%d", &T) ) {
        int n;
        while( T-- ) {
            scanf( "%d", &n );
            printf( "%d\n", factorial_digits(n) );
        }
    }
    return 0;
}

大数阶乘 @

输入

    每行一个整数 n

    1
    2
    3
    6
    18
    108

输出

    对每个 n，每行输出 n!

    1
    2
    6
    720
    6402373705728000
    1324641819451828974499891837121832599810209360673358065686551152497461815091591578895743130235002378688844343005686404521144382704205360039762937774080000000000000000000000000

#include <stdio.h>
#include <string.h>

#define BIGINT_RADIX 10000
#define RADIX_LEN 4
#define MAX_LEN (35660/RADIX_LEN+1)         // 10000! 有 35660 位

int     x[MAX_LEN + 1];

void bigint_print( const int x[], const int n ) {
    bool start_output = false;              // 用于跳过前导 0
    for( int i = n - 1; i >= 0; --i ) {
        if( start_output ) {                // 如果多余的 0 已经都跳过，则输出
            printf( "%04d", x[i] );
            continue;
        }
        if( x[i] > 0 ) {
            printf( "%d", x[i] );           // 本题输出比较坑爹，最高位数字有前导 0
            start_output = true;            // 碰到第一个非 0 的值，就说明多余的 0 已经都跳过
        }
    }
    if ( !start_output ) { printf("0"); }   // 当 x 全为 0 时
}

// 大整数乘法, x = x*y.
void bigint_mul( int x[], const int y ) {
    int c = 0;                              // carry
    for( int i = 0; i < MAX_LEN; ++i ) {    // 用 y，去乘以 x 的各位
        int tmp = x[i] * y + c;
        x[i] = tmp % BIGINT_RADIX;
        c    = tmp / BIGINT_RADIX;
    }
}

void bigint_factorial( int n, int x[] ) {
    memset( x, 0, sizeof(int)*(MAX_LEN+1) );
    x[0] = 1;
    for( int i = 2; i <= n; ++i ) {
        bigint_mul( x, i );
    }
}

int main() {
    int n;
    while ( 1 == scanf("%d", &n) ) {
        bigint_factorial( n, x );
        bigint_print( x, MAX_LEN + 1 ); printf("\n");
    }
    return 0;
}

5.4 Selected Problems @

Unix ls @

像 ls 一样格式化打印（主要处理 column 对齐问题）。

#include <iostream>
#include <string>
#include <algorithm>
using namespace std;

const int maxcol    = 60;
const int maxn      = 100+5;
string filenames[maxn];

void print( const string &s, int len, char extra ) {
    cout<< s;
    if( len < 0 ) { return; }
    for( int i = 0; i < len-s.length(); ++i ) {
        cout << extra;
    }
}

int main() {
    int n;
    while( cin >> n ) {
        int M = 0;
        for( int i = 0; i < n; ++i ) {
            cin >> filenames[i];
            M = max( M, (int)filenames[i].length() );
        }
        int cols = (maxcol-M)/(M+2) + 1, rows = (n-1)/cols + 1;
        print( "", 60, '-' );
        cout << "\n";
        sort( filenames, filenames+n );
        for( int r = 0; r < rows; ++r ) {
            for( int c = 0; c < cols; ++c ) {
                int idx = c * rows + r;
                if( idx < n ) {
                    print( filenames[idx],
                           c == cols-1? M : M+2,
                           ' ' );
                }
            }
            cout << "\n";
        }
    }
    return 0;
}

run it:

(echo "`ls|wc -l` `ls`") | path/to/our/own/ls
------------------------------------------------------------
LICENSE.txt  envs         lib          ssl
bin          etc          pkgs         var
conda-meta   include      share

database @

// UVa1592 Database
// Rujia Liu
// 本程序只是为了演示 STL 各种用法，效率较低。实践中一般用 C 字符串和哈希表来实现。

#include<iostream>
#include<cstdio>
#include<vector>
#include<string>
#include<map>
#include<sstream>
using namespace std;

typedef pair<int,int> PII;

const int maxr = 10000 + 5;
const int maxc = 10 + 5;

int m, n, db[maxr][maxc], cnt;

map<string, int> id;
int ID(const string& s) {
    if(!id.count(s)) {
        id[s] = ++cnt;
    }
    return id[s];
}

void find() {
    for(int c1 = 0; c1 < m; c1++)
        for(int c2 = c1+1; c2 < m; c2++) {
            map<PII, int> d;
            for(int i = 0; i < n; i++) {
                PII p = make_pair(db[i][c1], db[i][c2]);
                if(d.count(p)) {
                    printf("NO\n");
                    printf("%d %d\n", d[p]+1, i+1);
                    printf("%d %d\n", c1+1, c2+1);
                    return;
                }
                d[p] = i;
            }
        }
    printf("YES\n");
}


int main() {
    string s;
    while(getline(cin, s)) {
        stringstream ss(s);
        if(!(ss >> n >> m)) break;
        cnt = 0;
        id.clear();
        for(int i = 0; i < n; i++) {
            getline(cin, s);
            int lastpos = -1;
            for(int j = 0; j < m; j++) {
                int p = s.find(',', lastpos+1);
                if(p == string::npos) p = s.length();
                db[i][j] = ID(s.substr(lastpos+1, p - lastpos - 1));
                lastpos = p;
            }
        }
        find();
    }
    return 0;
}

PGA Tour Price Money @

// UVa207 PGA Tour Prize Money
// Rujia Liu
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cassert>
using namespace std;

#define REP(i,n) for(int i = 0; i < (n); i++)

const int maxn = 144;
const int n_cut = 70;

struct Player {
    char name;
    int amateur;
    int sc;
    int sc36, sc72, dq;
    int rnds;
} player[maxn];

int n;
double purse, p[n_cut];

bool cmp1(const Player& p1, const Player& p2) {
    if(p1.sc36 < 0 && p2.sc36 < 0) return false; // equal
    if(p1.sc36 < 0) return false; // p2 smaller
    if(p2.sc36 < 0) return true; // p1 smaller
    return p1.sc36 < p2.sc36;
}

bool cmp2(const Player& p1, const Player& p2) {
    if(p1.dq && p2.dq) {
        if(p1.rnds != p2.rnds) return p2.rnds < p1.rnds;
        if(p1.sc72 != p2.sc72) return p1.sc72 < p2.sc72;
        return strcmp(p1.name, p2.name) < 0;
    }
    if(p1.dq) return false;
    if(p2.dq) return true;
    if(p1.sc72 != p2.sc72) return p1.sc72 < p2.sc72;
    return strcmp(p1.name, p2.name) < 0;
}

void print_result() {
    printf("Player Name          Place     RD1  RD2");
    printf("  RD3  RD4  TOTAL     Money Won\n");
    printf("---------------------------------------");
    printf("--------------------------------\n");

    int i = 0, pos = 0;
    while(i < n) {
        if(player[i].dq) {
            printf("%s           ",player[i].name);
            REP(j,player[i].rnds) printf("%-5d", player[i].sc[j]);
            REP(j,4-player[i].rnds) printf("     ");
            printf("DQ\n");
            i++;
            continue;
        }

        int j = i;
        int m = 0; // number of tied players
        bool have_money = false;
        double tot = 0.0; // total pooled money
        while(j < n && player[i].sc72 == player[j].sc72) {
            if(!player[j].amateur) {
                m++;
                if(pos < n_cut) {
                    have_money = true; // yeah! they still have money
                    tot += p[pos++];
                }
            }
            j++;
        }

        // print player [i,j) together because they have the same rank
        int rank = i + 1; // rank of all these m players
        double amount = purse * tot / m; // if m=0, amount will be nan but we don't use it in that case :)
        while(i < j) {
            printf("%s ", player[i].name);
            char t;
            sprintf(t, "%d%c", rank, m > 1 && have_money && !player[i].amateur ? 'T' : ' ');
            printf("%-10s", t);
            REP(e,4) printf("%-5d", player[i].sc[e]);

            // with prize
            if(!player[i].amateur && have_money) {
                printf("%-10d", player[i].sc72);
                printf("$%9.2lf\n", amount / 100.0);
            } else
                printf("%d\n", player[i].sc72);
            i++;
        }
    }
}

int main() {
    int T;
    char s;

    gets(s);
    sscanf(s,"%d",&T);
    while(T--) {
        gets(s); // empty line

        // prize
        gets(s);
        sscanf(s,"%lf", &purse);
        REP(i,n_cut) {
            gets(s);
            sscanf(s, "%lf", &p[i]);
        }

        // players
        gets(s);
        sscanf(s, "%d", &n);
        assert(n <= 144);
        REP(k,n) {
            // read a 32-character line
            gets(s);

            // player name
            strncpy(player[k].name, s, 20);
            player[k].name = 0;
            player[k].amateur = 0;
            if(strchr(player[k].name, '*')) {
                player[k].amateur = 1;
            }

            // scores
            player[k].sc36 = player[k].sc72 = player[k].dq=0;
            memset(player[k].sc, -1, sizeof(player[k].sc));
            REP(i,4) {
                // raw score
                char t;
                REP(j,3) t[j] = s[20 + i*3 + j]; t = '\0';

                // parse
                if(!sscanf(t,"%d", &player[k].sc[i])) {
                    // DQ!
                    player[k].rnds = i;
                    player[k].dq = -1;
                    if(i < 2) player[k].sc36 = -1;
                    break; // skip other rounds (filled with -1, initially)
                } else {
                    player[k].sc72 += player[k].sc[i];
                    if(i < 2)
                        player[k].sc36 += player[k].sc[i];
                }
            }
        }

        // round 1
        sort(player, player+n, cmp1);
        assert(player[n_cut-1].sc36 >= 0);
        for(int i = n_cut-1; i < n; i++)
            if(i == n-1 || player[i].sc36 != player[i+1].sc36) { n = i+1; break; }

        // round 2
        sort(player, player+n, cmp2);

        // print result
        print_result();

        if(T) printf("\n");
    }

    return 0;
}

The Letter Crarrier’s Rounds, ACM/ICPC World Finals @

// UVa814 The Letter Carrier's Rounds
// Rujia Liu
#include<iostream>
#include<string>
#include<vector>
#include<set>
#include<map>
using namespace std;

void parse_address(const string& s, string& user, string& mta) {
    int k = s.find('@');
    user = s.substr(0, k);
    mta = s.substr(k+1);
}

int main() {
    int k;
    string s, t, user1, mta1, user2, mta2;
    set<string> addr;

    // 输入所有 MTA，转化为地址列表
    while(cin >> s && s != "*") {
        cin >> s >> k;
        while(k--) { cin >> t; addr.insert(t + "@" + s); }
    }

    while(cin >> s && s != "*") {
        parse_address(s, user1, mta1); // 处理发件人地址

        vector<string> mta; // 所有需要连接的mta，按照输入顺序
        map<string, vector<string> > dest; // 每个mta需要发送的用户
        set<string> vis;
        while(cin >> t && t != "*") {
            parse_address(t, user2, mta2); // 处理收件人地址
            if(vis.count(t)) continue;     // 重复的收件人
            vis.insert(t);
            if(!dest.count(mta2)) { mta.push_back(mta2); dest[mta2] = vector<string>(); }
            dest[mta2].push_back(t);
        }
        getline(cin, t); // 把"*"这一行的回车吃掉

        // 输入邮件正文
        string data;
        while(getline(cin, t) && t != '*') data += "     " + t + "\n";

        for(int i = 0; i < mta.size(); i++) {
            string mta2 = mta[i];
            vector<string> users = dest[mta2];
            cout << "Connection between " << mta1 << " and " << mta2 <<endl;
            cout << "     HELO " << mta1 << "\n";
            cout << "     250\n";
            cout << "     MAIL FROM:<" << s << ">\n";
            cout << "     250\n";
            bool ok = false;
            for(int i = 0; i < users.size(); i++) {
                cout << "     RCPT TO:<" << users[i] << ">\n";
                if(addr.count(users[i])) { ok = true; cout << "     250\n"; }
                else cout << "     550\n";
            }
            if(ok) {
                cout << "     DATA\n";
                cout << "     354\n";
                cout << data;
                cout << "     .\n";
                cout << "     250\n";
            }
            cout << "     QUIT\n";
            cout << "     221\n";
        }
    }
    return 0;
}

Urban Elevations, 1992 World Finals @

// UVa221 Urban Elevations
// Rujia Liu
#include<cstdio>
#include<algorithm>
using namespace std;

const int maxn = 100 + 5;

struct Building {
    int id;
    double x, y, w, d, h;
    bool operator < (const Building& rhs) const {
        return x < rhs.x || (x == rhs.x && y < rhs.y);
    }
} b[maxn];

int n;
double x[maxn*2];

bool cover(int i, double mx) {
    return b[i].x <= mx && b[i].x+b[i].w >= mx;
}

// 判断建筑物 i 在 x=mx 处否可见
bool visible(int i, double mx) {
    if(!cover(i, mx)) return false;
    for(int k = 0; k < n; k++)
        if(b[k].y < b[i].y && b[k].h >= b[i].h && cover(k, mx)) return false;
    return true;
}

int main() {
    int kase = 0;
    while(scanf("%d", &n) == 1 && n) {
        for(int i = 0; i < n; i++) {
            scanf("%lf%lf%lf%lf%lf", &b[i].x, &b[i].y, &b[i].w, &b[i].d, &b[i].h);
            x[i*2] = b[i].x; x[i*2+1] = b[i].x + b[i].w;
            b[i].id = i+1;
        }
        sort(b, b+n);
        sort(x, x+n*2);
        int m = unique(x, x+n*2) - x; // x 坐标排序后去重，得到 m 个坐标

        if(kase++) printf("\n");
        printf("For map #%d, the visible buildings are numbered as follows:\n%d", kase, b.id);
        for(int i = 1; i < n; i++) {
            bool vis = false;
            for(int j = 0; j < m-1; j++)
                if(visible(i, (x[j] + x[j+1]) / 2)) { vis = true; break; }
            if(vis) printf(" %d", b[i].id);
        }
        printf("\n");
    }
    return 0;
}

第六章，etc。放到 bonus 那边了。

✂️ 2016/08/06 上午 9:30:00 2. 二分搜索 Binary Search @

binary search @

// 如果找到 x，则返回其下标。 如果找不到 x 且 x 小于 array
// 中的一个或多个元素，则为一个负数，该负数是大于 x 的第一
// 个元素的索引的按位求补。 如果找不到 x 且 x 大于 array 中
// 的任何元素，则为一个负数，该负数是（最后一个元素的索引加 1）的按位求补。

#include <stdio.h>

int binary_search( const int A[], const int n, const int x ) {
    int left = 0, right = n-1, mid;
    while( left <= right ) {
        mid = left + (right - left) / 2;
        if( x > A[mid] ) {
            left = mid + 1;
        } else if(x < A[mid]) {
            right = mid - 1;
        } else {
            return mid;
        }
    }
    return -(left+1);           // instead of returning -1
}
// -(left+1) == ~left == ~(~(~left))，可以看到这个“编码” effective，而且直观。

int main() {
    int A[] = { 1,  5,  6,  9,  12,    18,    25,    73  };
    int x;
    while( scanf("%d", &x) == 1 ) {
        int pos = binary_search( A, sizeof(A)/sizeof(A[0]), x );
        for( int i = 0; i < sizeof(A)/sizeof(A[0]); ++i ) {
            printf( "[%3d]", A[i] );
        }
        printf( "\n" );
        if( pos >= 0 ) {
            printf( "%*s  ^  hit, pos=%d\n", pos*5, "", pos );
        } else {
            printf( "%*s  |  insert before, pos=%d\n", (-pos-1)*5, "", pos );
        }
    }
}

$ ./a.out

        7
                  right left
        [  1][  5][  6][  9][ 12][ 18][ 25][ 73]
                         |  insert before, pos=-4

        9
                     left/right
        [  1][  5][  6][  9][ 12][ 18][ 25][ 73]
                         ^  hit, pos=3

        1
        left/right
        [  1][  5][  6][  9][ 12][ 18][ 25][ 73]
          ^  hit, pos=0

        73
                                         left/right
        [  1][  5][  6][  9][ 12][ 18][ 25][ 73]
                                             ^  hit, pos=7

        98
                                           right  left
        [  1][  5][  6][  9][ 12][ 18][ 25][ 73]
                                                  |  insert before, pos=-9

        0

  right  left
        [  1][  5][  6][  9][ 12][ 18][ 25][ 73]
          |  insert before, pos=-1

学习 Binary Search 的通用模板，不再死循环 @

int binary_search( int array[], int length, int value )
{
    // 这两个判断不必要
    // if( length <= 0 ) { return -1; }
    // if( length == 1 ) { return array == value ? 0: -1; }

    int low = 0;
    int high = length-1;
    int mid;
    while( low <= high ) {
        mid = (low+high)/2;
        if( array[mid] == value ) {
            return mid;
        } else if( array[mid] > value ) {
            high = mid-1;
        } else {
            low  = mid+1;
        }
    }
    return -1;
}

什么情况下，mid-1 和 mid+1 不越界？length > 1。但还好有 left <= right 的判断，所以越界后，while 进不去。

感受一下 mid 的位置 @

中间有奇数个数字
[   0,  1,  2,  3,  4,  ... ]
    ^       *       ^

[   0,  1,  2,  3,  4,  5,  ... ]
        ^       *       ^

中间有偶数个数字
[   0,  1,  2,  3,  4,  5,  ... ]
    ^       *           ^

[   0,  1,  2,  3,  4,  5,  6,  ... ]
        ^       *           ^

中间啥都没有
[   0,  1,  ... ]
    ^   ^
    *

[   0,  ... ]
    ^
    ^
    *

总之因为 (left+right)/2 是向下 round（floor）。

需要注意的是 -3/2 = -1.5 = -1，-1/2 = -0.5 = 0；可见是向 0 round 的。

如果有负的 index
[      -1,  0,  ... ]
        ^   ^
            *

[  -2, -1,  0,  ... ]
    ^   ^
        *

+-----------------------------------------------------------------------------------------------+
|   -2, 1 ->    (left+right)/2          = -1/2 = -0.5               = 0,    round to zero       |
|               left + (right-left)/2   = -2 + (1-(-2))/2 = -2+1.5  = -1,   more to the left    |
+-----------------------------------------------------------------------------------------------+

但其实……怎么 round 是无所谓的。我这里只是让自己感受一下 mid 的位置。面试的时候可以快速的找到中点（而不是用 index 算）。

讲解 Search in Rotated Sorted Array 等 5-7 道高频二分搜索题 @

Search in Rotated Sorted Array @

class Solution {
public:
    int search(vector<int>& nums, int target) {
        return search( nums, 0, nums.size(), target );
    }
    int search( vector<int> &nums, int left, int right, int target, int binarysearch = 0 ) {
        if( binarysearch == 1 ) {
            int mid;
            while( left <= right ) {
                mid = (left+right)/2;
                if( target == nums[mid] ) {
                    return mid;
                } else if( target < nums[mid] ) {
                    right = mid-1;
                } else {
                    left = mid+1;
                }
            }
            return -1;
        }
        if( left > right ) { return -1; }
        if( left < 0 ) { left = 0; }
        if( right >= nums.size() ) { right = nums.size()-1; }

        int mid = (left+right)/2;
        if( target == nums[left] ) { return left; }
        if( target == nums[right] ) { return right; }
        if( target == nums[mid] ) { return mid; }

        if( nums[left] < nums[right] ) {
            //          case 1
            //
            //              /
            //             /
            //            /
            //           /
            //          /
            //
            if( target < nums[left] || target > nums[right] ) { return -1; }
            if( target < nums[mid] ) {
                return search( nums, left,  mid-1, target, 1 ); // ordinary binary search
            } else {
                return search( nums, mid+1, right, target, 1 ); // ordinary binary search
            }
        } else if( nums[left] < nums[mid] /* && nums[left] > nums[right] */ ) {
            //          case 2
            //
            //            /
            //           /
            //          /
            //              /
            //             /
            //
            if( nums[left] < target && target < nums[mid] ) {
                return search( nums,  left, mid-1, target, 1 ); // ordinary binary search
            } else {
                return search( nums, mid+1, right, target );
            }
        } else if( nums[right] > nums[mid] /* nums[left] > nums[right] */ ) {
            //          case 3
            //
            //           /
            //          /
            //              /
            //             /
            //            /
            //
            if( nums[mid] < target && target < nums[right] ) {
                return search( nums, mid+1, right, target, 1 ); // ordinary binary search
            } else {
                return search( nums,  left, mid-1, target );
            }
        } else {
            //cout << "what...?!\n";
            return -1;
        }
    }
};

refs and see also

Search in Rotated Sorted Array II @

Follow up for “Search in Rotated Sorted Array”:

What if duplicates are allowed?
Would this affect the run-time complexity? How and why?
Write a function to determine if a given target is in the array.

class Solution {
public:
    bool search(vector<int>& nums, int target) {
        int low = 0;
        int high = nums.size()-1;
        int mid;
        while( low <= high ) {
            if( nums[low] < nums[high] && (target<nums[low]||nums[high]<target) ) {
                return false;
            }
            // if dupilicates, remove the duplication
            while ( low < high && nums[low] == nums[high] ) {
                ++low;
            }
            mid = (low+high)/2;
            if ( nums[mid] == target || nums[low] == target || nums[high] == target ) {
                return true;
            }
            // left, not rotated
            if ( nums[low] < target && target < nums[mid] ) {
                high = mid-1;
                continue;
            }
            // right, not rotated
            if ( nums[mid] < target && target < nums[high] ) {
                low = mid+1;
                continue;
            }
            // rotated
            if  ( nums[low]  > nums[mid] ){ high = mid-1; continue; }
            if  ( nums[high] < nums[mid] ){ low  = mid+1; continue; }
            ++low;
        }
        return false;
    }
};

refs and see also

81. Search in Rotated Sorted Array II | LeetCode OJ

Find Minimum in Rotated Sorted Array @

Suppose a sorted array is rotated at some pivot unknown to you beforehand.

(i.e., 0 1 2 4 5 6 7 might become 4 5 6 7 0 1 2).

Find the minimum element.

You may assume no duplicate exists in the array.

class Solution {
public:
    int findMin(vector<int>& nums) {
        return findMin( nums, 0, nums.size()-1 );
    }
    int findMin( vector<int>& nums, int low, int high ) {
        int mid = (low+high)/2;
        if( mid == low || mid == high ) { return min( nums[low], nums[high] ); }
        if( nums[low] < nums[high] ) {
            return nums[low];
        } else {
            if( nums[low] < nums[mid] ) {
                return min( findMin( nums, mid+1, high ), nums[low] );
            } else {
                return min( findMin( nums, low, mid-1 ), nums[mid] );
            }
        }
    }
};

refs and see also

153. Find Minimum in Rotated Sorted Array | LeetCode OJ

Find Minimum in Rotated Sorted Array II @

The array may contain duplicates.

没有通过 ==

class Solution {
public:
    int findMin(vector<int>& nums) {
        return findMin( nums, 0, nums.size()-1 );
    }
    int findMin( vector<int>& nums, int low, int high ) {
        if( low > high ) { return INT_MAX; }
        int mid = (low+high)/2;
        if( mid == low || mid == high ) { return min( nums[low], nums[high] ); }
        if( nums[low] < nums[high] ) {
            return nums[low];
        } else {
            while ( low < high && nums[low] == nums[high] ) {
                ++low;
            }
            mid = (low+high)/2;
            if( mid == low || mid == high ) { return min( nums[low], nums[high] ); }
            if( nums[low] < nums[mid] ) {
                return min( findMin( nums, mid+1, high ), nums[low] );
            } else {
                return min( findMin( nums, low, mid-1 ), nums[mid] );
            }
        }
    }
};

Convert Sorted Array to Binary Search Tree @

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {

        if(nums.size()==0){
            return NULL;
        }
        if(nums.size()==1){
            return new TreeNode(nums);
        }
        int mid = nums.size()/2;

        TreeNode *node = new TreeNode(nums[mid]);

        vector<int>::const_iterator first = nums.begin();
        vector<int>::const_iterator last  = nums.begin()+mid;

        vector<int> v(first, last);
        node->left = sortedArrayToBST(v);

        if (mid==nums.size()-1){
            node->right = NULL;
        } else {
            first = nums.begin()+mid+1;
            last = nums.end();
            vector<int> v(first, last);
            node->right = sortedArrayToBST(v);
        }
        return node;
    }
};

Convert Sorted List to Binary Search Tree 和这个类似，我加了一层转换就 pass 了：

TreeNode* sortedListToBST(ListNode* head) {
    vector<int> nums;
    while( head ) {
        nums.push_back( head->val );
        head = head->next;
    }
    return sortedArrayToBST( nums );
}

refs and see also

Binary search algorithm - Wikipedia, the free encyclopedia

✂️ 2016/08/07 上午 9:30:00 3. 二叉树问题与分治算法 Binary Tree & Divide Conquer @

二叉树的节点定义 @

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode( int x ) : val(x), left(nullptr), right(nullptr) { }
}

递归版的都很容易 @

（Recursive solution is trivial ['trɪvɪəl], could you do it iteratively ['itə,reitivli]?）

void traversal( TreeNode *root, vector<int> &result ) {
    if( !root ) { return; }
    // 如果先序（中序和后序只是调整一下位置）
    result.push_back( root->val );
    traversal( root->left,  result );
    traversal( root->right, result );
}

Iterative 算法伪码 @

【从维基百科查到的 iterative 方法的算法伪码】

DPS: Depth-first search
BPS: Breath-first search
--------------------------------------------
iterativePreorder(node)
    if (node = null)
        return
    s ← empty stack
    s.push(node)
    while (not s.isEmpty())
        node ← s.pop()
        visit(node)
        if (node.right ≠ null)
            s.push(node.right)
        if (node.left ≠ null)
            s.push(node.left)
--------------------------------------------
iterativeInorder(node)
   s ← empty stack

   while (not s.isEmpty() or node ≠ null)
       if (node ≠ null)
           s.push(node)
           node ← node.left
       else
           node ← s.pop()
           visit(node)
           node ← node.right
--------------------------------------------
iterativePostorder(node)
    s ← empty stack                                               O  1      X-> go left/down
    lastNodeVisited ← null                                       /          X-> go right?
    while (not s.isEmpty() or node ≠ null)                   2  O           X-> go up.
        if (node ≠ null)                                       / \
            s.push(node)                                   3  X-> O  4
            node ← node.left                                     / \
        else                                                5  O    O  7
            peekNode ← s.peek()                              /     /
            // if right child exists and traversing node    X 6   X 8
            // from left child, then move right
            if (peekNode.right ≠ null and lastNodeVisited ≠ peekNode.right)
                node ← peekNode.right
            else
                visit(peekNode)
                lastNodeVisited ← s.pop()
--------------------------------------------
levelorder(root)
    q ← empty queue
    q.enqueue(root)
    while (not q.isEmpty())
        node ← q.dequeue()
        visit(node)
        if (node.left ≠ null)
            q.enqueue(node.left)
        if (node.right ≠ null)
            q.enqueue(node.right)

Code Template @

#include <stdio.h>
#include <iostream>
#include <queue>
#include <stack>
#include <vector>
#define nullptr 0
using namespace std;

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x = -1 ) : val(x), left(NULL), right(NULL) {}  // added default ctor
};
void link( TreeNode &root, TreeNode * left, TreeNode *right ) {
    root.left  = left;
    root.right = right;
}

class Solution {
    public:
    vector<vector<int> > levelOrder( TreeNode *root );
    ...
};

int main() {
    TreeNode node;
    for( int i = 0; i < 10; ++i ) { node[i].val = i; }
    printf( "         0               \n"
            "        / \\             \n"
            "       /   \\            \n"
            "      1     2            \n"
            "    /  \\     \\         \n"
            "   3    4     5          \n"
            "   \\    /    / \\       \n"
            "    6  7    8   9        \n"   );
    link(   node,     &node,      &node     );
    link(   node,     &node,      &node     );
    link(   node,         0,      &node     );
    link(   node,         0,      &node     );
    link(   node,     &node,          0     );
    link(   node,     &node,      &node     );
    link(   node,         0,          0     );
    link(   node,         0,          0     );
    link(   node,         0,          0     );
    link(   node,         0,          0     );

    Solution sol;
    vector<vector<int> > ret = sol.levelOrder( &node );
    for( int i = 0; i < ret.size(); ++i ) {
        for( int j = 0; j < ret[i].size(); ++j ) {
            cout << " " << ret[i][j];
        }
        cout << "\n";
    }
    return 0;
}

refs and see also

二叉树的深度优先遍历 Binary Tree DFS Traversal @

先序 / 中序 / 后序 Preorder / inorder / postorder @

先序遍历 @

用栈 @

// Time: O(n), Space: O(n)
vector<int> preorderTravesal( TreeNode *root ) {
    vector<int> result;
    stack<TreeNode *> s;
    if( root ) { s.push(root); }                // nullptr 一定不要 push！
    while( !s.empty() ) {
        root = s.top(); s.pop();
        result.push_back( root->val );
        if( root->right ) { s.push( root->right); }   // 这里不要疏忽了
        if( root->left  ) { s.push( root->left ); }
    }
    return result;
}

Morris 先序遍历 @

参考 Morris Traversal方法遍历二叉树（非递归，不用栈，O(1) 空间） - AnnieKim - 博客园。

要使用 O(1) 空间进行遍历，最大的难点在于，遍历到子节点的时候怎样重新返回到父节点（假设节点中没有指向父节点的 p 指针），由于不能用栈作为辅助空间。为了解决这个问题，Morris 方法用到了线索二叉树（threaded binary tree）的概念。在 Morris 方法中不需要为每个节点额外分配指针指向其前驱（predecessor）和后继节点（successor），只需要利用叶子节点中的左右空指针指向某种顺序遍历下的前驱节点或后继节点就可以了。

moris preorder

// Time: O(n), Space: O(1)
vector<int> preorderTraversal( TreeNode *root ) {
    vector<int> result;
    TreeNode *cur = root; *prev = nullptr;

    while( cur ) {
        if( cur->left ) {
            result.push_back( cur->val );
            prev    = cur;
            cur     = cur->right;
        } else {
            // 查找前驱
            TreeNode *node = cur->left;
            while( node->right && node->right != cur ) {
                node = node->right;
            }
            if( !node->right ) {
                result.push_back( cur->val );
                node->right = cur;
                prev        = cur;
                cur         = cur->left;
            } else {
                node->right = nullptr;
                cur = cur->right;
            }
        }
    }
    return result;
}

中序（inorder）遍历 ❤️ @

用栈 @

    =while { if / else }=

     down to left loop
     +------->-------+
     |              \|/
     |               V
   +-----+       +---|---------------+
   |while|       |  i f  -->-- else  |
   +-^---+       +---|---------- ----+
     |               V          | go to right subtree
     +-------<-------+--<-------+

    +--+                           +----+
    |if|                           |else|
    +--+                           +----+
                X
               /                           i.  pop
              X                            ii. visit
             /                             iii. go right
            ?

vector<int> inorderTraveral( TreeNode *root ) {
    vector<int> result;
    stack<TreeNode *> s;
    while( !s.empty() || root ) {
        if( root ) {
            s.push( root );                 // 计划处理 root（当前）
            root = root->left;              // 但先处理左节点
        } else {
            root = s.top(); s.pop();        // 处理 root（当前），它的左子树已经处理完了~
            result.push_back( root->val );
            root = root->right;             // 然后移到右边
        }
    }
    return result;
}

Moris @
```
TODO
```
红色是为了定位到某个节点，黑色线是为了找到前驱节点。

moris inorder

后序遍历 @

用栈 @

vector<int> postorderTraversal( TreeNode *root ) {
    vector<int> ret;
    stack<TreeNode *> s;
    TreeNode *pre = nullptr;
    while( !s.empty() || root ) {
        if( root ) {                                    // keep going the left
            s.push( root );
            root = root->left;
        } else {
            TreeNode *root = s.top();
            if( root->right && root->right != pre ) {   // left way is finsised, keep going to the right way
                root = root->right;
            } else {
                ret.push_back( root->val );             // both left and right has been accessed.
                pre = root; s.pop();                    // root == s.top();
            }
        }
    }
    return ret;
}

Another idea, by Chenhao. @

vector<int> postorderTraversal( TreeNode *root ) {
    vector<int> ret;
    stack<TreeNode *> s;
    if( root ) { s.push( root ); }
    while( !s.empty() ) {
        root = s.top(); s.pop();
        ret.push_back( root->val );
        if( root->left  ) { s.push( root->left ); }     // 和先序遍历几乎一模一样!!! 只是调换了顺序.
        if( root->right ){ s.push( root->right ); }
    }
    std::reverse( ret.begin(), ret.end() );             // the trick
    return ret;
}

    A                   postorder:  DFEBCA
   / \
  B   C
 / \
D   E
   /
  F

stack       vector      action
-----       ---------   -------------
||          []
|A|         []          push root
|BC|        [A]         not empty, pop A, log A, push B, C
|B|         [AC]        not empty, pop C, log C, no push
|DE|        [ACB]       not empty, pop B, log B, push D, E
|DF|        [ACBE]      not empty, pop E, log E, push F
|D|         [ACBEF]     not empty, pop F, log F, no push
||          [ACBEFD]    not empty, pop D, log D, no push
||          [DFEBCA]    empty, reverse vec, return

Morris @

class Solution {
    void reverse_right_chain(TreeNode *x, TreeNode *y) {
        TreeNode *p = x, *q = x->right, *right;
        while (p != y) {
            right = q->right;
            q->right = p;
            p = q;
            q = right;
        }
    }
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> ret;
        TreeNode aux(0), *p = &aux;
        aux.left = root;
        aux.right = NULL;
        while (p) {
            TreeNode *q = p->left;
            if (q) {
                while (q->right && q->right != p) q = q->right;
                if (q->right == p) {
                    reverse_right_chain(p->left, q);
                    for (TreeNode *r = q; ; r = r->right) {
                        ret.push_back(r->val);
                        if (r == p->left) break;
                    }
                    reverse_right_chain(q, p->left);
                    q->right = NULL;
                } else {
                    q->right = p;
                    p = p->left;
                    continue;
                }
            }
            p = p->right;
        }
        return ret;
    }
};

threaded tree @

#include <stddef.h>                             // for NULL
#include <stdio.h>

typedef int elem_t;
typedef struct tbt_node_t {
    int ltag;                                   // 0 for child, 1 for thread
    int rtag;
    struct tbt_node_t *left;                    // left child, or pre
    struct tbt_node_t *right;                   // right child , or succ
    elem_t elem;                                // node
} tbt_node_t;

static void in_thread(tbt_node_t *p, tbt_node_t **pre);
static tbt_node_t *first(tbt_node_t *p);
static tbt_node_t *next(const tbt_node_t *p);

void create_in_thread(tbt_node_t *root) {
    tbt_node_t *pre=NULL;
    if( !root ) {                   // 非空二叉树，线索化
        in_thread( root, &pre );    // threaded in_order traversal
        pre->right = NULL;          // the only last work to do
        pre->rtag = 1;
    }
}

void in_order( tbt_node_t *root, int(*visit)(tbt_node_t*) ) {
    for( tbt_node_t *p = first(root); p; p = next(p) ) { visit(p); }
}

self->left -> pre
                            B (pre)
                          .^ \
                         .    \
                         .     \
                           . . .D (p)
                               /
                              /
                            ~~~~ no left child, make it point to it's pre
pre->right -> self
                              A (p)
                             /^
                            /   .
                           /      .
                          B        .
                           \      .
                            D.. . (pre)
                             \
                            ~~~~ no right child, make it point to it's succ

static void in_thread( tbt_node_t *p, tbt_node_t **pre ) {
    if( p ) {
        in_thread( p->left, pre );
        if( !p->left ) {                        // left child point to pre
            p->left = *pre;
            p->ltag = 1;
        }
        /* 建立前驱结点的后继线索 */

        if( (*pre) && !(*pre)->right ) {        // pre's right child point to self
            (*pre)->right = p;
            (*pre)->rtag = 1;
        }
        *pre = p;
        in_thread( p->right, pre );
    }
}


// 寻找线索二叉树的中序下的第一个结点.
// p 线索二叉树中的任意一个结点
// return 此线索二叉树的第一个结点
static tbt_node_t *first(tbt_node_t *p) {
    if( !p ) { return NULL; }
    while( p->ltag == 0 ) {
        p = p->left;            // left-most node, (may not be leaf, (it may has right child))
    }
    return p;
}

static tbt_node_t *next( const tbt_node_t *p ) {
    assert( p );
    if( p->rtag == 0 ) {
        return first(p->right);
    } else {
        return p->right;        // succ
    }
}

rebuild tree ♥️ @

原理以及人工推演 @

                      +---------------------------------------------+
                      |                                             |
                      v                                             |
{pre}       =   [    pre,+---+  {leftpre},      {rightpre}  ];      |
{in}        =   [ {leftin},  +----->in,<-----+  {rightin}   ];      |
{post}      =   [ {leftpost},   {rightpost}, +-+post        ];      |
                                                   ^                |
                                                   |                |
                                                   +----------------+

手工推演一下：

pre = "ABDGCEF";
in  = "DGBAECF";

    DGBAECF(ABDGCEF)    ->          A               ->          A
        / \                                                    / \
       /   \                                                  /   \
  DGB(BDG) ECF(CEF)     ->      B       C                    B     C
                            DG(DG)  E       F               D     E F
                                                             G

先序、中序字符串到后序字符串 ♥️ @

#include <stdio.h>
#include <string.h>

void build_post( const char * pre, const char *in, const int n, char *post ) {
    if(n <= 0) { return; }
    int left_len = strchr(in, pre[0]) - in;
    post[n - 1] = pre[0];                   // you can put this line before/after recursion.
    build_post( pre+1,          in,             left_len,       post );
    build_post( pre+left_len+1, in+left_len+1,  n-left_len-1,   post+left_len );
}

int main() {
    puts(
    " tree:                        \n"
    "            A                 \n"
    "           / \\               \n"
    "          /   \\              \n"
    "         B     C              \n"
    "        /     / \\            \n"
    "       D     E   F            \n"
    "        \\                    \n"
    "         G                    \n" );
    const char *pre     = "ABDGCEF";
    const char *in      = "DGBAECF";
    char        post[8] = { 0     };
    //                    "GDBEFCA";
    build_post( pre, in, strlen(pre), post  );
    printf( "pre:  %s\n", pre               );
    printf( "in:   %s\n", in                );
    printf( "post: %s\n", post              );
}

output:

 tree:
            A
           / \
          /   \
         B     C
        /     / \
       D     E   F
        \
         G

pre:  ABDGCEF
in:   DGBAECF
post: GDBEFCA

生成树，105. Construct Binary Tree from Preorder and Inorder Traversal ♥️ @

void rebuild( const char *pre, const char *in, int n, bt_node_t **root ) {
    if( n <= 0 || !pre || !in ) {                                       // 检查终止条件
        return;
    }

    *root = (bt_node_t*) malloc(sizeof(bt_node_t));                     // 获得前序遍历的第一个结点
    (*root)->elem = *pre;
    (*root)->left = NULL;
    (*root)->right = NULL;

    int left_len = strchr( in, pre ) - in;
    rebuild( pre + 1, in,                                               // 重建左子树
             left_len,          &((*root)->left) );
    rebuild( pre + left_len + 1, in + left_len + 1,                     // 重建右子树
             n - left_len - 1,  &((*root)->right) );
}

// Construct Binary Tree from Preorder and Inorder Traversal

// iterative
class Solution {
public:
    TreeNode *buildTree(vector<int> &preorder, vector<int> &inorder) {
        if (preorder.empty()) return nullptr;
        auto i = preorder.begin(), j = inorder.begin();
        auto root = new TreeNode(*i++);
        stack<TreeNode *> s;
        s.push(root);
        while (i != preorder.end()) {
            auto x = s.top();
            if (x->val != *j) {
                x->left = new TreeNode(*i++);
                x = x->left;
                s.push(x);
            } else {
                s.pop();
                ++j;
                if (s.empty() || s.top()->val != *j) {
                    x->right = new TreeNode(*i++);
                    x = x->right;
                    s.push(x);
                }
            }
        }
        return root;
    }
};

// recursive
#define FOR(i, a, b) for (decltype(b) i = (a); i < (b); i++)
#define REP(i, n) FOR(i, 0, n)

class Solution {
public:
    TreeNode *buildTree(vector<int> &preorder, vector<int> &inorder) {
        return f(&preorder[0], &*preorder.end(), &inorder[0], &*inorder.end());
    }
    TreeNode *f(int *l, int *h, int *ll, int *hh) {
        if (l == h)
            return NULL;
        auto r = new TreeNode(*l);
        int *m = find(ll, hh, *l);
        r->left = f(l+1, l+1+(m-ll), ll, m);
        r->right = f(l+1+(m-ll), h, m+1, hh);
        return r;
    }
};

refs and see also

Construct Binary Tree from Preorder and Inorder Traversal | LeetCode OJ

双亲表示法 @

#include <iostream>
#include <string>
#include <sstream>
#include <algorithm>
#include <iterator>
#include <assert.h>
#include <stdio.h>
using namespace std;

const int maxv = 100 + 10;
int in_order    [   maxv    ];
int post_order  [   maxv    ];
int lch         [   maxv    ];
int rch         [   maxv    ];

int n;

bool read_list( int *a ) {
    string line;
    if( !getline( cin, line ) ) { return false; }
    stringstream ss( line );
    n = 0;
    int x;
    while( ss >> x ) { a[n++] = x; }
    return n > 0;
}

//  in_order[L1..R1] 和 post_order[L2..R2] 建成一颗树，返回树根
int build( int L1, int R1, int L2, int R2 ) {
    if( L1 > R1 ) { return 0; }
    int root = post_order[ R2 ];
    int p = L1;
    while( in_order[p] != root ) { ++p; }
    int cnt = p-L1;
    lch[ root ] = build( L1, p-1, L2, L2+cnt-1 );
    rch[ root ] = build( p+1, R1, L2+cnt, R2-1 );
    return root;
}

string print( int root, string pad ) {
    if( root == 0 ) { return pad; }
    const static string space = "        ";
    char buf;
    sprintf( buf, "%d", root );
    string result = pad + space + string(buf);
    result += "\n";
    result += print( lch[root], pad );
    result += print( rch[root], pad+space+space );
    return result;
}

int best, best_sum;

//          u -> root
void dfs( int u, int sum ) {
    sum += u;
    if( !lch[u] && !rch[u] ) { // leaf
        if( sum < best_sum || (sum == best_sum && u < best) ) {
            best = u;
            best_sum = sum;
        }
    }
    if( lch[u] ) { dfs( lch[u], sum ); }
    if( rch[u] ) { dfs( rch[u], sum ); }
}

int main() {
    while( read_list( in_order ) ) {
        read_list( post_order );
        build( 0, n-1, 0, n-1 );
        best_sum = -1;
        dfs( post_order[n-1], 0 );
        cout << best << "\n";
        cout << print( post_order[n-1], "" );
        copy( lch, lch+n, ostream_iterator<int>(cout, " ") );
        cout <<"\n";
        copy( rch, rch+n, ostream_iterator<int>(cout, " ") );
        cout <<"\n";
    }
    return 0;
}

二叉树的宽度优先遍历 Binary Tree BFS Traversal @

就是层序遍历（level order traversal）

递归版本 @

// Time: O(n), Space: O(n)
vector<vector<int> > levelOrder( TreeNode *root ) {
    vector<vector<int> > result;
    traverse( root, 1, result );
    return result;
}

// level is IMPORTANT!
void traverse( TreeNode *root, size_t level, vector<vector<int> > &result ) {
    if( !root ) { return; }
    if( level - 1 >= result.size() ) {
        result.push_back( vector<int>() );                  // 也可以用 resize( level );
    }
    result[level-1].push_back( root->val );
    traverse( root->left,   level+1, result );
    traverse( root->right,  level+1, result );
}

迭代版本 1 @

// Time: O(n), Space: O(1)
vector<vector<int> > levelOrder( TreeNode *root ) {
    vector<vector<int> > ret;
    if( !root ) { return ret; };
    queue<TreeNode *> cur, next;
    cur.push( root );
    while( !cur.empty() ) {
        vector<int> level;
        while( !cur.empty() ) {
            root = cur.front(); cur.pop();
            level.push_back( root->val );
            if( root->left  ) { next.push( root->left  ); }
            if( root->right ) { next.push( root->right ); }
        }
        ret.push_back( level );
        swap( cur, next );
    }
    return ret;
}

迭代版本 2 @

vector<vector<int> > levelOrder( TreeNode *root ) {
    vector<vector<int> > ret;
    if( !root ) { return ret; }
    queue<TreeNode *> q;
    q.push( root );
    q.push( nullptr );                          // indicate end of cur level
    vector<int> cur;
    while( !q.empty() ) {
        root = q.front(); q.pop();
        if( root ) {
            cur.push_back( root->val );
            if ( root->left  ) { q.push( root->left  ); }
            if ( root->right ) { q.push( root->right ); }
        } else if( !q.empty() ) {
            if( !cur.empty() ) {
                ret.push_back( cur );
                cur.clear();
            }
            q.push( nullptr );                  // indicate end of cur level
        }
    }
    if( !cur.empty() ) { ret.push_back( cur ); }
    return ret;
}

refs and see also

二叉搜索树 Binary Search Tree @
- What is BST (wikipedia) @
  
  In computer science, binary search trees (BST), sometimes called ordered or sorted binary trees, are a particular type of containers: data structures that store “items” (such as numbers, names etc.) in memory. They allow fast lookup, addition and removal of items, and can be used to implement either dynamic sets of items, or lookup tables that allow finding an item by its key (e.g., finding the phone number of a person by name).
  
  The major advantage of binary search trees over other data structures is that the related sorting algorithms and search algorithms such as in-order traversal can be very efficient; they are also easy to code.
  
  Binary search trees are a fundamental data structure used to construct more abstract data structures such as sets, multisets, and associative arrays. Some of their disadvantages are as follows:
  
  The shape of the binary search tree depends entirely on the order of insertions and deletions, and can become degenerate. 树的结构跟数据插入删除顺序相关，可能退化。解决方案是平衡二叉树。
  
  When inserting or searching for an element in a binary search tree, the key of each visited node has to be compared with the key of the element to be inserted or found. 不是随机访问。
  
  The keys in the binary search tree may be long and the run time may increase. 如果 key 的比较很耗时，那就很糟。
  
  After a long intermixed sequence of random insertion and deletion, the expected height of the tree approaches square root of the number of keys, √n, which grows much faster than log n. 深度的预期是 sqrt(n) 比最好的 log(n) 差很多。不过这一点好像还是在说 degenerate……
  
  删除操作比较麻烦，分三种情况：
  
  Deleting a node with no children: simply remove the node from the tree.
  
  Deleting a node with one child: remove the node and replace it with its child.
  
  Deleting a node with two children: call the node to be deleted N. Do not delete N. Instead, choose either its in-order successor node or its in-order predecessor node, R. Copy the value of R to N, then recursively call delete on R until reaching one of the first two cases. If you choose in-order successor of a node, as right sub tree is not NIL (Our present case is node has 2 children), then its in-order successor is node with least value in its right sub tree, which will have at a maximum of 1 sub tree, so deleting it would fall in one of the first 2 cases.
  
  Deleting a node with two children from a binary search tree. First the rightmost node in the left subtree, the inorder predecessor 6, is identified. Its value is copied into the node being deleted. The inorder predecessor can then be easily deleted because it has at most one child. The same method works symmetrically using the inorder successor labelled 9. 这其实是在找一个比删掉节点（7）小（当然是小）但经可能大的能够接替 7 的工作的节点。这个节点在左边最右。这是如图所示。
  
  Tree rotations are very common internal operations in binary trees to keep perfect, or near-to-perfect, internal balance in the tree.
- Unique Binary Search Trees，多少个变形？ @
  
  Given n, how many structurally unique BST’s (binary search trees) that store values 1…n?
  
  For example, Given n = 3, there are a total of 5 unique BST’s.
  
  1 3 3 2 1 \ / / / \ \ 3 2 1 1 3 2 / / \ \ 2 1 2 3
  
  【数组为 1, 2, ... 以 i 为根节点的树，左子树由 `[i, i-1]` 构成，右子树为 `[i+1, n]` 构成。】如果 n 为 1： 1 如果 n 为 2： 1 或者 2 \ / 2 1 f(2) = f(0) * f(1), 1 为根的情况 + f(1) * f(0), 2 为根 f(3) = f(0) * f(2), 1 为根 + f(1) * f(1), 2 为根 + f(2) * f(0), 3 为根
  
  递推公式为 f(i) = sum{ f(k-1)*f(i-k) } for k = 1..i，这是一个一维动态规划。
  
  int numTrees( int n ) { vector<int> f( n+1, 0 ); f[0] = f[1] = 1; for( int i = 2; i <= n; ++i ) { for( int k = 1; k <= n; ++k ) { f[i] += f[k-1] * f[i-k]; } } return f[n]; }
  
  refs and see also
  
  Unique Binary Search Trees | LeetCode OJ
- Validate Binary Search Tree @
  
  bool isValidBST( TreeNode *root ) { // leetcode 的 test case 里有 0xFFFFFFFF 和 0x7FFFFFFF， // 简单考虑，直接变成 long long 再比较 return isValidBST( root, LLONG_MIN, LLONG_MAX ); } // 看是否在【界定】之内 bool isValidBST( TreeNode *root, long long min, long long max ) { if( !root ) { return true; } long long val = root->val; return val > min && val < max && isValidBST( root->left, min, root->val ) && isValidBST( root->right, root->val, max ); }
  
  refs and see also
  
  Validate Binary Search Tree | LeetCode OJ
- Convert Sorted Array to Binary Search Tree @
  
  Given an array where elements are sorted in ascending order, convert it to a height balanced BST.
  
  dup problem, same idea. (思路是一样的，不过那边更直白。) 首先要明确，这个 BST 不唯一。
  
  TreeNode * sortedArrayToBST( vector<int> &nums ) { return sortedArrayToBST( nums.begin(), nums.end() ); } template<typename RandomAccessIterator> TreeNode * sortedArrayToBST( RandomAccessIterator first, RandomAccessIterator last ) { if( length <= 0 ) { return nullptr; } const auto length = distance( first, last ); RandomAccessIterator mid = first + length/2; TreeNode *root = new TreeNode( *mid ); root->left = sortedArrayToBST( first, mid ); root->right = sortedArrayToBST( mid+1, last ); return root; }
  
  refs and see also
  
  Convert Sorted Array to Balanced Binary Search Tree (BST) – LeetCode
  
  Convert Sorted Array to Binary Search Tree | LeetCode OJ
- Convert Sorted List to Binary Search Tree @
  
  这里和上面不同的是，list 不能随机存取。最省力的方法是，先把 list 转成 array……
  
  不用这种化归的偷懒策略，有两种思路：
  
  分治法，自顶向下 O(n²)，O(logn) @
  
  // 分治法，类似于 Convert Sorted Array to Binary Search Tree， // 自顶向下，时间复杂度O(n^2)，空间复杂度O(logn) class Solution { public: TreeNode *sortedListToBST( ListNode *head ) { return sortedListToBST( head, listLength(head) ); } TreeNode *sortedListToBST( ListNode *head, int len ) { if (len == 0) { return nullptr; } if (len == 1) { return new TreeNode(head->val); } TreeNode *root = new TreeNode( nth_node (head, len / 2 + 1)->val ); root->left = sortedListToBST( head, len / 2 ); root->right = sortedListToBST( nth_node(head, len / 2 + 2), (len - 1) / 2); return root; } int listLength( ListNode *node ) { int n = 0; while( node ) { node = node->next; ++n; } return n; } ListNode *nth_node( ListNode *node, int n ) { while( --n ) { node = node->next; } return node; } };
  
  自底向上 O(n)，O(logn) ♥️ @
  
  As usual, the best solution requires you to think from another perspective. In other words, we no longer create nodes in the tree using the top-down approach. We create nodes bottom-up, and 【assign them to its parents】. The bottom-up approach enables us to access the list in its order while creating nodes.
  
  Isn’t the bottom-up approach neat? Each time you are stucked with the top-down approach, give bottom-up a try. Although bottom-up approach is not the most natural way we think, it is extremely helpful in some cases. However, you should prefer top-down instead of bottom-up in general, since the latter is more difficult to verify in correctness.
  
  Below is the code for converting a singly linked list to a balanced BST. Please note that the algorithm requires the list’s length to be passed in as the function’s parameters. The list’s length could be found in O(N) time by traversing the entire list’s once. The recursive calls traverse the list and create tree’s nodes by the list’s order, which also takes O(N) time. Therefore, the overall run time complexity is still O(N).
  
  BinaryTree* sortedListToBST(ListNode *& list, int start, int end) { if (start > end) return NULL; int mid = start + (end - start) / 2; // same as (start+end)/2, avoids overflow BinaryTree *leftChild = sortedListToBST(list, start, mid-1); BinaryTree *parent = new BinaryTree(list->data); parent->left = leftChild; list = list->next; parent->right = sortedListToBST(list, mid+1, end); return parent; } BinaryTree* sortedListToBST(ListNode *head, int n) { return sortedListToBST(head, 0, n-1); }
  
  这是什么解法呢？ @
  
  // Convert Sorted List to Binary Search Tree class Solution { ListNode *l; TreeNode *f(int n) { if (! n) return 0; auto x = new TreeNode(0); x->left = f(n/2); x->val = l->val; l = l->next; x->right = f(n-n/2-1); return x; } public: TreeNode *sortedListToBST(ListNode *head) { l = head; int n = 0; while (head) { head = head->next; n++; } return f(n); } };
  
  refs and see also
  
  Convert Sorted List to Binary Search Tree | LeetCode OJ
  
  Convert Sorted List to Balanced Binary Search Tree (BST) – LeetCode

分治 Divide & Conquer @

pow(x, n) @

实现 power(x, n) 即 xⁿ

思路：

n 为奇数，xⁿ = x * x^n-1
n 为偶数，xⁿ = x^n/2 * x^n/2

或者 xⁿ = x^n/2 * x^n/2 * x^n%2

// Time: O(logn), Space: O(1)
double pow( double x, int n ) {
    if( n < 0  ) { return 1.0 / pow( x, -n); }
    if( n == 0 ) { return 1.0; }
    double v = pow( x, n/2 );
    if( n%2 == 0 ) {                    // divide & conquer
        return v * v;
    } else {
        return v * v * x;
    }
}

sqrt(x) @

int sqrt( int x ) {
    int left = 1, right = x / 2 + 1, mid;
    if( x < 2 ) { return x; }                   // ?<0->..., 0->0, 1->1
    while( left <= right ) {
        mid = (left+right)/2;
        if( x / mid > mid ) {
            left = mid+1;
        } else if ( x / mid < mid) {
            right = mid-1;
        } else {
            // 9/3 == 3, 10/3 == 3, 15/3 > 3, so sqrt(15) = 4
            break; // return mid;
        }
    }
    return mid;
}

chess covering @
dup?
```
input:

    3
    1
    2
    3

output:

    1
    5
    21
```
本题的棋盘是 2^k x 2^k，很容易想到用分治法。把棋盘切成 4 块，则每一块都是 2^k-1 x 2^k-1 的。有黑格的那一块可以递归解决，但其他 3 块并没有黑格子，应该怎么办呢？可以构造出一个黑格子，在中心放一个 L 型牌，其它 3 块也变成了子问题。递归边界不难得出，当 k=1 时 1 块 L 型牌就够了。

本题只需要求总数，不需要求具体怎么摆放，因此简化很多。根据上面的思路，设 f(k) 表示棋盘是 2^k x 2^k 时所需 L 型牌的总数，可得递推公式 f(k) = 4f(k-1)+1。

注意，2¹⁰⁰ 是一个很大的数，本题需要处理大数。

schedule ♥️ @

有 2^k 个运动员参加循环比赛，需要设计比赛日程表。要求如下：

每个选手必须与其他 n-1 个选手各赛一次
每个选手一天只能赛一次
比赛一共进行 n-1 天

按此要求设计一张比赛日程表，它有 n 行和 n-1 列，第 i 行第 j 列为第 i 个选手第 j 天遇到的对手。

input:

    只有一个数 k，0 < k < 9，且 k 为自然数。

    1

output:

    一张比赛日程表，它有 n 行和 n-1 列
    （不算第一列，第一列表示选手的编号），第 i 行第j 列为
    第 i 个选手第 j 天遇到的对手。相邻的两个整数用空格隔开。

    1 2
    2 1

分析

根据分而治之的思想，可从其中一半选手 (2^k-1 位) 的比赛日程，推导出全体选手的日程，最终细分到只有两位选手的比赛日程。

所示是 k=3 时的一个可行解，它是由 4 块拼起来的。左上角是 k=2 时的一组解，左下角是由左上角每个数加 4 得到，而右上角、右下角分别由左下角、左上角复制得到。

1   2   3   4 | 5   6   7   8
2   1   4   3 | 6   5   8   7
3   4   1   2 | 7   8   5   6
4   3   2   1 | 8   7   6   5
--------------+--------------
5   6   7   8 | 1   2   3   4
6   5   8   7 | 2   1   4   3
7   8   5   6 | 3   4   1   2
8   7   6   5 | 4   3   2   1

#include<stdio.h>
#include<stdlib.h>

#define MAXN 512                    // N=2^k, 0<k<9
short schedule[MAXN][MAXN];

void dc(const int k) {
    int i, j, t;
    int n, n2; /* 当前的n，即将扩展的n */

    /* k=1，即两个人时，日程表可以直接写出 */
    n=2;
    schedule[0][0]=1; schedule[0][1]=2;
    schedule[1][0]=2; schedule[1][1]=1;

    // 迭代处理，依次处理2^2....2^k个选手的比赛日程
    for(t = 1; t < k; t++, n *= 2) {
        n2 = n * 2;
        //填左下角元素
        for(i = n; i < n2; i++)
            for(j = 0; j < n; j++)
                schedule[i][j] = schedule[i-n][j] + n;

        //将左下角元素抄到右上角
        for(i = 0; i < n; i++)
            for(j = n; j < n2; j++)
                schedule[i][j] = schedule[i+n][j-n];

        //将左上角元素抄到右下角
        for(i = n; i < n2; i++)
            for(j = n;j < n2; j++)
                schedule[i][j] = schedule[i-n][j-n];
    }
}

/* 另一个版本 */
void dc2(const int k) {
    int i, j, r;
    int n;
    const int N = 1 << k;

    /* 第一列是选手的编号 */
    for(i = 0; i < N; i++) schedule[i][0] = i + 1;
    schedule[0][1] = 1;  /* 当 k=0时，只有一个人 */

    for (n = 2; n <= N; n *= 2) {  /* 方块大小, 2, 4, 8 */
        const int half = n / 2;
        for (r = 0; r < N; r += n) { /* 方块所在行 */
            for (i = r; i <= r + half -1; i++) {  /* 左上角小方块的所有行 */
                for (j = 0; j < half; j++) {  /* 左上角小方块的所有行 */
                    /* 右下角 <-- 左上角 */
                    schedule[i + half][j + half] = schedule[i][j];
                    /* 右上角 <-- 左下角 */
                    schedule[i][j + half] = schedule[i + half][j];
                }
            }
        }
    }
}

int main(){
    int k, N;
    int i,j;

    scanf("%d",&k);
    N = 1 << k;

    dc(k);
    // dc2(k);

    // 输出日程表
    for(i = 0; i < N; i++) {
        for(j = 0; j < N; j++) printf("%d ", schedule[i][j]);
        printf("\n");
    }
    return 0;
}

refs and see also

✂️ 2016/00/00 上午 9:30:00 0. Sortings @

util: print.cpp @

#include <stdio.h>
#include <algorithm>

void print( int A[], int n, const char *msg = 0 ) {
    using namespace std;
    int h = *max_element(A, A+n);
    if( h >= 10 ) { return; }
    if( msg ) { printf( "==== %s ====\n", msg ); }
    for( int i = 0; i < n+1; ++i ) {
        for( int j = 0; j < h; ++j ) {
            if( i + A[j] == h+1 ) {
                printf( " |%d| ", A[j] );
            } else if( i+A[j] < h+1 ) {
                printf( "     " );
            } else {
                printf( " |X| " );
            }
        }
        printf( "\n" );
    }
    for( int i = 0; i < n; ++i ) { printf( "-----" ); }     printf( "\n" );
    for( int i = 0; i < n; ++i ) { printf( "  %d  ", i ); } printf( "\t(index)\n\n\n" );
}

effect

                            |9|
                            |X|                 |8|
                            |X|                 |X|  |7|
                       |6|  |X|                 |X|  |X|
                       |X|  |X|  |5|            |X|  |X|
                       |X|  |X|  |X|       |4|  |X|  |X|
                  |3|  |X|  |X|  |X|       |X|  |X|  |X|
             |2|  |X|  |X|  |X|  |X|       |X|  |X|  |X|
             |X|  |X|  |X|  |X|  |X|  |1|  |X|  |X|  |X|
            ---------------------------------------------
              0    1    2    3    4    5    6    7    8     (index)

insertion sort @

straight insertion sort @

#include <stdio.h>
#include <algorithm>
#include "print.cpp"

using namespace std;

void straight_insertion_sort( int A[], const int start, const int end ) {
    int tmp;
    int i, j;

    // insert ith element
    for (i = start + 1; i < end; i++) {
        tmp = A[i];
        for (j = i - 1; j >= start && tmp < A[j]; j--) {    // to the left
            A[j + 1] = A[j];                                // j->j+1
        }
        A[j + 1] = tmp;
    }
}

int main() {
    int A[] = { 3, 2, 6, 9, 5, 1, 4, 8, 7  };
    int n = sizeof(A)/sizeof(A[0]);
    straight_insertion_sort( A, 0, n );
}

which is better, why?

for( int j = i - 1; j >= start && tmp < A[j]; --j ) {   // good
    A[j + 1] = A[j];
}

for( int j = i - 1; j >= start && tmp < A[j]; ) {
    A[j + 1] = A[j];
    --j;                                                // better in some aspect
}

pretty output @

==== before sorting ====

                |9|
                |X|                 |8|
                |X|                 |X|  |7|
           |6|  |X|                 |X|  |X|
           |X|  |X|  |5|            |X|  |X|
           |X|  |X|  |X|       |4|  |X|  |X|
 |3|       |X|  |X|  |X|       |X|  |X|  |X|
 |X|  |2|  |X|  |X|  |X|       |X|  |X|  |X|
 |X|  |X|  |X|  |X|  |X|  |1|  |X|  |X|  |X|
---------------------------------------------
  0    1    2    3    4    5    6    7    8     (index)

==== i: 1, j+1: 0 ====

                |9|
                |X|                 |8|
                |X|                 |X|  |7|
           |6|  |X|                 |X|  |X|
           |X|  |X|  |5|            |X|  |X|
           |X|  |X|  |X|       |4|  |X|  |X|
      |3|  |X|  |X|  |X|       |X|  |X|  |X|
 |2|  |X|  |X|  |X|  |X|       |X|  |X|  |X|
 |X|  |X|  |X|  |X|  |X|  |1|  |X|  |X|  |X|
---------------------------------------------
  0    1    2    3    4    5    6    7    8     (index)

==== i: 2, j+1: 2 ====

                |9|
                |X|                 |8|
                |X|                 |X|  |7|
           |6|  |X|                 |X|  |X|
           |X|  |X|  |5|            |X|  |X|
           |X|  |X|  |X|       |4|  |X|  |X|
      |3|  |X|  |X|  |X|       |X|  |X|  |X|
 |2|  |X|  |X|  |X|  |X|       |X|  |X|  |X|
 |X|  |X|  |X|  |X|  |X|  |1|  |X|  |X|  |X|
---------------------------------------------
  0    1    2    3    4    5    6    7    8     (index)

==== i: 3, j+1: 3 ====

                |9|
                |X|                 |8|
                |X|                 |X|  |7|
           |6|  |X|                 |X|  |X|
           |X|  |X|  |5|            |X|  |X|
           |X|  |X|  |X|       |4|  |X|  |X|
      |3|  |X|  |X|  |X|       |X|  |X|  |X|
 |2|  |X|  |X|  |X|  |X|       |X|  |X|  |X|
 |X|  |X|  |X|  |X|  |X|  |1|  |X|  |X|  |X|
---------------------------------------------
  0    1    2    3    4    5    6    7    8     (index)

==== i: 4, j+1: 2 ====

                     |9|
                     |X|            |8|
                     |X|            |X|  |7|
                |6|  |X|            |X|  |X|
           |5|  |X|  |X|            |X|  |X|
           |X|  |X|  |X|       |4|  |X|  |X|
      |3|  |X|  |X|  |X|       |X|  |X|  |X|
 |2|  |X|  |X|  |X|  |X|       |X|  |X|  |X|
 |X|  |X|  |X|  |X|  |X|  |1|  |X|  |X|  |X|
---------------------------------------------
  0    1    2    3    4    5    6    7    8     (index)

==== i: 5, j+1: 0 ====

                          |9|
                          |X|       |8|
                          |X|       |X|  |7|
                     |6|  |X|       |X|  |X|
                |5|  |X|  |X|       |X|  |X|
                |X|  |X|  |X|  |4|  |X|  |X|
           |3|  |X|  |X|  |X|  |X|  |X|  |X|
      |2|  |X|  |X|  |X|  |X|  |X|  |X|  |X|
 |1|  |X|  |X|  |X|  |X|  |X|  |X|  |X|  |X|
---------------------------------------------
  0    1    2    3    4    5    6    7    8     (index)

==== i: 6, j+1: 3 ====

                               |9|
                               |X|  |8|
                               |X|  |X|  |7|
                          |6|  |X|  |X|  |X|
                     |5|  |X|  |X|  |X|  |X|
                |4|  |X|  |X|  |X|  |X|  |X|
           |3|  |X|  |X|  |X|  |X|  |X|  |X|
      |2|  |X|  |X|  |X|  |X|  |X|  |X|  |X|
 |1|  |X|  |X|  |X|  |X|  |X|  |X|  |X|  |X|
---------------------------------------------
  0    1    2    3    4    5    6    7    8     (index)

==== i: 7, j+1: 6 ====

                                    |9|
                               |8|  |X|
                               |X|  |X|  |7|
                          |6|  |X|  |X|  |X|
                     |5|  |X|  |X|  |X|  |X|
                |4|  |X|  |X|  |X|  |X|  |X|
           |3|  |X|  |X|  |X|  |X|  |X|  |X|
      |2|  |X|  |X|  |X|  |X|  |X|  |X|  |X|
 |1|  |X|  |X|  |X|  |X|  |X|  |X|  |X|  |X|
---------------------------------------------
  0    1    2    3    4    5    6    7    8     (index)

==== i: 8, j+1: 6 ====

                                         |9|
                                    |8|  |X|
                               |7|  |X|  |X|
                          |6|  |X|  |X|  |X|
                     |5|  |X|  |X|  |X|  |X|
                |4|  |X|  |X|  |X|  |X|  |X|
           |3|  |X|  |X|  |X|  |X|  |X|  |X|
      |2|  |X|  |X|  |X|  |X|  |X|  |X|  |X|
 |1|  |X|  |X|  |X|  |X|  |X|  |X|  |X|  |X|
---------------------------------------------
  0    1    2    3    4    5    6    7    8     (index)

==== after sorting ====

                                         |9|
                                    |8|  |X|
                               |7|  |X|  |X|
                          |6|  |X|  |X|  |X|
                     |5|  |X|  |X|  |X|  |X|
                |4|  |X|  |X|  |X|  |X|  |X|
           |3|  |X|  |X|  |X|  |X|  |X|  |X|
      |2|  |X|  |X|  |X|  |X|  |X|  |X|  |X|
 |1|  |X|  |X|  |X|  |X|  |X|  |X|  |X|  |X|
---------------------------------------------
  0    1    2    3    4    5    6    7    8     (index)

binary insertion sort @

void straight_insertion_sort( int A[], const int start, const int end ) {
    int tmp;
    int i, j;
    for (i = start + 1; i < end; i++) {
        tmp = A[i];
        int left = start, right = i-1, mid;
        while( left <= right ) {
            mid = (left+right)/2;
            if( tmp < A[mid] ) {
                right = mid - 1;
            } else {
                left = mid + 1;     // 大于或者等于，都向右倾斜
            }
        }
        for( j = i - 1; j >= left; --j ) {
            A[j + 1] = A[j];
        }
        A[left] = tmp;
    }
}

+-------------------------------+
|   find 4                      |
|                       R   L   |
|   0   1   2   4   4   4   6   |
|                           ^   |
+-------------------------------+

L=0, R=6        ->      M=3

L           M           R
0   1   2   4   4   4   6

                L   M   R               target >= a[M], L=M+1
0   1   2   4   4   4   6

                        L
                        M
                        R               target <  a[M], R=M-1
0   1   2   4   4   4   6

                    R   L               a[R] == 4
0   1   2   4   4   4   6

shell insertion sort @

从对直接插入排序的分析得知，其算法时间复杂度为 O(n^2^)，但是，若待排序记录序列为“正序”时，其时间复杂度可提高至 O(n)。

由此可设想，若待排序记录序列按关键字“基本有序”，
即序列中具有下列特性 `R~i~.key < max{ R~j~.key }`, j<i 的
记录较少时，直接插入排序的效率就可大大提高。

从另一方面 来看，由于直接插入排序算法简单，则在 n 值很小时效率也比
较高。希尔排序正是从这两点分析出发对直接插入排序进行改
进得到的一种插入排序方法。

希尔排序 (Shell Sort) 的基本思想是：设待排序元素序
列有 n 个元素，首先取一个整数 gap = n/3+1 作为间隔，
将全部元素分为 gap 个子序列，所有距离为 gap 的元素放在
同一个子序列中，在每一个子序列中分别施行直接插入排
序。然后缩小间隔 gap，取 gap = n/3+1, 重复上述的子序列
划分和排序工作，直到最后取 gap = 1，将所有元素放在同一
个序列中排序为止。

```cpp
// 和一趟直接插入排序相比，仅有一点不同，就是前后元素的间距是 gap 而不是 1
// [start, end)
// gap 间隔
static void shell_insert( int A[], const int start, const int end, const int gap ) {
    int tmp;
    int i, j;
    for( int i = start + gap; i < end; ++i ) {
        tmp = A[i];
        for( int j = i - gap; j>=start && A[j] > tmp; j -= gap ) {
            A[j + gap] = A[j];
        }
        A[j + gap] = tmp;
    }
}

void shell_sort( int A[], const int start, const int end ) {
    int gap = end - start;
    while( gap > 1 ) {
        gap = gap / 3 + 1;
        shell_insert( A, start, end, gap );
    }
}
```

if `gap <- gap/3+1 > 1`, then it's buggy.

```
gap: 4 2 1
gap: 5 2 1
gap: 7 3 2 1
gap: 8 3 2 1
gap: 9 4 2 1
```

exchange sort @

bubble sort @

void bubble_sort( int A[], const int start, const int end ) {
    int exchange;
    int tmp;
    // i is the element to set, in this loop
    for ( int i = start; i < end - 1; i++) {
        exchange = 0;
        for ( int j = end - 1; j > i; j--) {        // 发生逆序，交换
            if (A[j - 1] > A[j]) {
                tmp = A[j - 1];
                A[j - 1] = A[j];
                A[j] = tmp;
                exchange = 1;
            }
        }
        if( exchange == 0 ) { return; }             // 本趟无逆序，停止处理
    }
}

quick sort @

void quick_sort( int A[], const int start, const int end ) {
    if( start < end - 1 ) {                                     // 至少两个元素
        const int pivot_pos = partition( A, start, end );
        quick_sort( A, start, pivot_pos );
        quick_sort( A, pivot_pos + 1, end );
    }
}

int partition( int A[], const int start, const int end ) {
    int i = start;
    int j = end - 1;
    const int pivot = A[i];

    while( i < j ) {
        while( j > i && A[j] >= pivot ) { j--; }    // no need to move to left
        A[i] = A[j];                                // move
        while( i < j && A[i] <= pivot ) { i++; }    // no need to move to right
        A[j] = A[i];                                // move to right
    }
    A[i] = pivot;
    return i;
}

log:
            -------------------------------------
            p0:  3  2   6   9   5   1   4   8   7
            p1:  1  2   3   9   5   6   4   8   7
            ------------+------------------------
            p0:  1  2   |
            p1:  1  2   |
            ------------+------------------------
            p0:         |   9   5   6   4   8   7
            p1:         |   7   5   6   4   8   9
            ------------+-----------------------+
            p0:             7   5   6   4   8   |
            p1:             4   5   6   7   8   |
            ----------------------------+-------+
            p0:             4   5   6   |
            p1:             4   5   6   |
            ----------------+-----------+--------
            p0:             |   5   6
            p1:             |   5   6
            ----------------+--------------------

analysis

    pivot = 3
    ---------

            3   2   6   9   5   1   4   8   7
            i=0                             j=8         --j
                                        j=7             --j
                                    j=6                 --j
                                j=5
            1   2   6   9   5   1   4   8   7           A[i=0]  =   A[j=5]  = 1
            i=0                                         ++i
                i=1                                     ++i
                    i=2
            1   2   6   9   5   6   4   8   7           A[j=5]  =   A[i=2]  = 6
                    i=2         j=5                     i < j   ->  true, loop, --j
                            j=4                         --j
                        j=3                             --j
                    j=2                                 A[i=2]  =   A[j=2]  = 6
            1   2   6   9   5   6   4   8   7           i < j   -> false, loop end
            1   2   3   9   5   6   4   8   7           A[i]    =   pivot

    pivot = 1
    ---------

            1   2
            i=0 j=1                                     --j
            j=0
            1   2                                       A[i=0]  =   A[j=0]
            1   2                                       A[i=0]  =   A[j=0]
            1   2                                       i < j   ->  false
            1   2                                       A[i=0]  =   pivot

    pivot = 9
    ---------

            9   5   6   4   8   7
            i=0                 j=5
            7   5   6   4   8   7                       A[i=0]  =   A[j=5]  = 7
            i=0                                         ++i
                i=1                                     ++i
                    i=2                                 ++i
                        i=3                             ++i
                            i=4                         ++i
                                i=5
            7   5   6   4   8   7
                                i=5
                                j=5                     i < j   ->  false
            7   5   6   4   8   9                       A[i=5]  =   pivot   = 9

    p1:  7 5 6 4 8 9

    p0:  7 5 6 4 8
    p1:  4 5 6 7 8

    p0:  4 5 6
    p1:  4 5 6

    p0:  5 6
    p1:  5 6

refs and see also

selection sort @

simple selection sort @

void simple_selection_sort( int A[], int start, int end ) {
    int tmp;

    // A[i] will be put at right position
    for( int i = start; i < end; ++i ) {
        int k = i;
        for( int j = i + 1; j < end; ++j ) {
            if( A[j] < A[k] ) { k = j; }          // 在 a[i] 到 a[end-1] 中寻找最小元素
        }
        if( k != i ) {
            tmp = A[i]; A[i] = A[k]; A[k]= tmp;
        }
    }
}

heap sort @

#include <stdio.h>
#include "heap.c"

int cmp( const int *x, const int *y ) {
    int sub = *x - *y;
    return sub < 0 ? 1 : sub > 0 ? -1 : 0;
}

void heap_sort( int *a, const int n, int (*cmp)(const int *, const int *) ) {
    heap_t h;
    h.cmp = cmp;
    h.elems = a;
    h.size = h.capacity = n;

    int i = (h.size - 2)/2;             // 找最初调整位置：最后分支结点
    while( i >= 0 ) {                   // 自底向上逐步扩大形成堆
        heap_sift_down( &h, i );
        --i;
    }

    int tmp;
    for( int i = h.size - 1; i > 0; --i ) {
        tmp = h.elems[i]; h.elems[i] = h.elems; h.elems = tmp;
        h.size = i;                     // 相当于 --h.size
        heap_sift_down( &h, 0 );
    }
}

int main() {
    int A[] = { 3, 2, 6, 9, 5, 1, 4, 8, 7  };
    int n = sizeof(A)/sizeof(A[0]);
    heap_sort( A, n, &cmp );
}

 3 2 6 9 5 1 4 8 7
before sift at 3
 3 2 6 9 5 1 4 8 7
 3 2 6 9 5 1 4 8 7
before sift at 2
 3 2 6 9 5 1 4 8 7
 3 2 6 9 5 1 4 8 7
before sift at 1
 3 2 6 9 5 1 4 8 7
 3 9 6 8 5 1 4 2 7
before sift at 0
 3 9 6 8 5 1 4 2 7
 9 8 6 7 5 1 4 2 3
before sift at 0
 3 8 6 7 5 1 4 2
 8 7 6 3 5 1 4 2
before sift at 0
 2 7 6 3 5 1 4
 7 5 6 3 2 1 4
before sift at 0
 4 5 6 3 2 1
 6 5 4 3 2 1
before sift at 0
 1 5 4 3 2
 5 3 4 1 2
before sift at 0
 2 3 4 1
 4 3 2 1
before sift at 0
 1 3 2
 3 1 2
before sift at 0
 2 1
 2 1
before sift at 0
 1
 1
 1 2 3 4 5 6 7 8 9

merge sort @

//  input: tmp[i/j]
//                         start       mid         end
//                           ^          ^
//                          [i]        [j]
//                            \        /
//                              \     /
//                                \ /
//                                 +
//  output:  A[i/j]                |
//                         start   |   mid         end
//                           ^     |
//                           |     |
//                          [k]--<-+
//
static void merge( int A[], int tmp[],
                   const int start,
                   const int mid,
                   const int end )
{
    for ( int i = 0; i < end; ++i ) {
        tmp[i] = A[i];
    }

    int i, j, k;
    for( i = start, j = mid, k = start; i < mid && j < end; k++ ) {
        if (tmp[i] < tmp[j]) {
            A[k] = tmp[i++];
        } else {
            A[k] = tmp[j++];
        }
    }
    while (i < mid) { A[k++] = tmp[i++]; }
    while (j < end) { A[k++] = tmp[j++]; }
}

void merge_sort( int A[], int tmp[], const int start, const int end ) {
    //  first   last
    if( start < end-1 ) {                       // more than one element
        const int mid = (start + end) / 2;
        merge_sort( A, tmp, start, mid );
        merge_sort( A, tmp, mid, end );
        merge( A, tmp, start, mid, end );
    }
}

merging: 0, 1, 2
merging: 2, 3, 4
merging: 0, 2, 4
merging: 4, 5, 6
merging: 7, 8, 9
merging: 6, 7, 9
merging: 4, 6, 9
merging: 0, 4, 9

    ==== before sorting ====

                    |9|
                    |X|                 |8|
                    |X|                 |X|  |7|
               |6|  |X|                 |X|  |X|
               |X|  |X|  |5|            |X|  |X|
               |X|  |X|  |X|       |4|  |X|  |X|
     |3|       |X|  |X|  |X|       |X|  |X|  |X|
     |X|  |2|  |X|  |X|  |X|       |X|  |X|  |X|
     |X|  |X|  |X|  |X|  |X|  |1|  |X|  |X|  |X|
    ---------------------------------------------
      0    1    2    3    4    5    6    7    8     (index)

    ==== start: 0, mid: 1, end: 2 ====

                    |9|
                    |X|                 |8|
                    |X|                 |X|  |7|
               |6|  |X|                 |X|  |X|
               |X|  |X|  |5|            |X|  |X|
               |X|  |X|  |X|       |4|  |X|  |X|
          |3|  |X|  |X|  |X|       |X|  |X|  |X|
     |2|  |X|  |X|  |X|  |X|       |X|  |X|  |X|
     |X|  |X|  |X|  |X|  |X|  |1|  |X|  |X|  |X|
    ---------------------------------------------
      0    1    2    3    4    5    6    7    8     (index)
      ^----^----^

    ==== start: 2, mid: 3, end: 4 ====

                    |9|
                    |X|                 |8|
                    |X|                 |X|  |7|
               |6|  |X|                 |X|  |X|
               |X|  |X|  |5|            |X|  |X|
               |X|  |X|  |X|       |4|  |X|  |X|
          |3|  |X|  |X|  |X|       |X|  |X|  |X|
     |2|  |X|  |X|  |X|  |X|       |X|  |X|  |X|
     |X|  |X|  |X|  |X|  |X|  |1|  |X|  |X|  |X|
    ---------------------------------------------
      0    1    2    3    4    5    6    7    8     (index)
                ^----^----^

    ==== start: 0, mid: 2, end: 4 ====

                    |9|
                    |X|                 |8|
                    |X|                 |X|  |7|
               |6|  |X|                 |X|  |X|
               |X|  |X|  |5|            |X|  |X|
               |X|  |X|  |X|       |4|  |X|  |X|
          |3|  |X|  |X|  |X|       |X|  |X|  |X|
     |2|  |X|  |X|  |X|  |X|       |X|  |X|  |X|
     |X|  |X|  |X|  |X|  |X|  |1|  |X|  |X|  |X|
    ---------------------------------------------
      0    1    2    3    4    5    6    7    8     (index)
      ^---------^---------^

    ==== start: 4, mid: 5, end: 6 ====

                    |9|
                    |X|                 |8|
                    |X|                 |X|  |7|
               |6|  |X|                 |X|  |X|
               |X|  |X|       |5|       |X|  |X|
               |X|  |X|       |X|  |4|  |X|  |X|
          |3|  |X|  |X|       |X|  |X|  |X|  |X|
     |2|  |X|  |X|  |X|       |X|  |X|  |X|  |X|
     |X|  |X|  |X|  |X|  |1|  |X|  |X|  |X|  |X|
    ---------------------------------------------
      0    1    2    3    4    5    6    7    8     (index)
                          ^----^----^

    ==== start: 7, mid: 8, end: 9 ====

                    |9|
                    |X|                      |8|
                    |X|                 |7|  |X|
               |6|  |X|                 |X|  |X|
               |X|  |X|       |5|       |X|  |X|
               |X|  |X|       |X|  |4|  |X|  |X|
          |3|  |X|  |X|       |X|  |X|  |X|  |X|
     |2|  |X|  |X|  |X|       |X|  |X|  |X|  |X|
     |X|  |X|  |X|  |X|  |1|  |X|  |X|  |X|  |X|
    ---------------------------------------------
      0    1    2    3    4    5    6    7    8     (index)
                                         ^----^----^

    ==== start: 6, mid: 7, end: 9 ====

                    |9|
                    |X|                      |8|
                    |X|                 |7|  |X|
               |6|  |X|                 |X|  |X|
               |X|  |X|       |5|       |X|  |X|
               |X|  |X|       |X|  |4|  |X|  |X|
          |3|  |X|  |X|       |X|  |X|  |X|  |X|
     |2|  |X|  |X|  |X|       |X|  |X|  |X|  |X|
     |X|  |X|  |X|  |X|  |1|  |X|  |X|  |X|  |X|
    ---------------------------------------------
      0    1    2    3    4    5    6    7    8     (index)
                                    ^----^---------^

    ==== start: 4, mid: 6, end: 9 ====

                    |9|
                    |X|                      |8|
                    |X|                 |7|  |X|
               |6|  |X|                 |X|  |X|
               |X|  |X|            |5|  |X|  |X|
               |X|  |X|       |4|  |X|  |X|  |X|
          |3|  |X|  |X|       |X|  |X|  |X|  |X|
     |2|  |X|  |X|  |X|       |X|  |X|  |X|  |X|
     |X|  |X|  |X|  |X|  |1|  |X|  |X|  |X|  |X|
    ---------------------------------------------
      0    1    2    3    4    5    6    7    8     (index)
                          ^---------^--------------^

    ==== start: 0, mid: 4, end: 9 ====

                                             |9|
                                        |8|  |X|
                                   |7|  |X|  |X|
                              |6|  |X|  |X|  |X|
                         |5|  |X|  |X|  |X|  |X|
                    |4|  |X|  |X|  |X|  |X|  |X|
               |3|  |X|  |X|  |X|  |X|  |X|  |X|
          |2|  |X|  |X|  |X|  |X|  |X|  |X|  |X|
     |1|  |X|  |X|  |X|  |X|  |X|  |X|  |X|  |X|
    ---------------------------------------------
      0    1    2    3    4    5    6    7    8     (index)
      ^-------------------^------------------------^

    ==== after sorting ====

                                             |9|
                                        |8|  |X|
                                   |7|  |X|  |X|
                              |6|  |X|  |X|  |X|
                         |5|  |X|  |X|  |X|  |X|
                    |4|  |X|  |X|  |X|  |X|  |X|
               |3|  |X|  |X|  |X|  |X|  |X|  |X|
          |2|  |X|  |X|  |X|  |X|  |X|  |X|  |X|
     |1|  |X|  |X|  |X|  |X|  |X|  |X|  |X|  |X|
    ---------------------------------------------
      0    1    2    3    4    5    6    7    8     (index)

radix sort @

conclusion @

排序方法	平均时间	最坏情况	辅助存储	是否稳定
直接插入排序	O(n²)	O(n²)	O(1)	是
折半插入排序	O(n²)	O(n²)	O(1)	是
希尔排序	N/A	N/A	O(1)	否
冒泡排序	O(n²)	O(n²)	O(1)	是
快速排序	O(nlogn)	O(n²)	O(logn)	否
简单选择排序	O(n²)	O(n²)	O(1)	否
堆排序	O(nlogn)	O(nlogn)	O(1)	否
二路归并	O(nlogn)	O(nlogn)	O(n)	是
基数排序	O(d*(n+R))	O(d*(n+R))	O(R)	是

✂️ 2016/00/00 上午 9:30:00 0. Brute Force @

Brute-force search @
In computer science, brute-force search or exhaustive search, also known as generate and test, is a very general problem-solving technique that consists of systematically enumerating all possible candidates for the solution and checking whether each candidate satisfies the problem’s statement.

Brute-force search is also useful as a baseline method when benchmarking other algorithms or metaheuristics. Indeed, brute-force search can be viewed as the simplest metaheuristic. Brute force search should not be confused with backtracking, where large sets of solutions can be discarded without being explicitly enumerated (as in the textbook computer solution to the eight queens problem above). The brute-force method for finding an item in a table — namely, check all entries of the latter, sequentially — is called linear search.

In order to apply brute-force search to a specific class of problems, one must implement four procedures, first, next, valid, and output. These procedures should take as a parameter the data P for the particular instance of the problem that is to be solved, and should do the following:
- first (P): generate a first candidate solution for P.
- next (P, c): generate the next candidate for P after the current one c.
- valid (P, c): check whether candidate c is a solution for P.
- output (P, c): use the solution c of P as appropriate to the application.
```
c ← first(P)
while c ≠ Λ do
    if valid(P,c) then output(P, c)
    c ← next(P,c)
end while
```
Combinatorial explosion, or the curse of dimensionality.

refs and see also
- Brute-force search - Wikipedia, the free encyclopedia

简单枚举 @

Division, abcde/fghij = n, a~j -> 0~9, n = 2..79 @

fghij × {2, 3, 4, … } = {xxxxx, …}, then test 0~9

#include <iostream>
#include <vector>
#include <utility> // pair
#include <stdio.h>

using namespace std;

bool five( int n ) {
    if( n < 1234 || n > 98765   ) { return false;   }
    int numpad = { 0 };
    if( n < 9876                ) { ++numpad;    }
    while( n ) {
        if( ++numpad[n%10] >= 2 ) { return false; }
        n /= 10;
    }
    return true;
}

bool ten( int n1, int n2, int buf[] ) {
    if( !five(n1) || !five(n2) ) { return false; }
    int numpad = { 0 };
    while( n1 ) {
        if( ++numpad[n1%10] >= 2 ) { return false; }
        n1 /= 10;
    }
    while( n2 ) {
        if( ++numpad[n2%10] >= 2 ) { return false; }
        n2 /= 10;
    }
    return true;
}

int main() {

    vector<pair<int, int> > result;

    int fghij = 1234;                               // 01234, but careful, not octal!
    for( int f = fghij; f <= 98765/2; ++f ) {
        if( !five(f) ) { continue; }
        for( int j = 2; j <= 79; ++j ) {
            int a = f * j;
            if( a > 98765 ) { break; }
            if( !five(a) ) {
                continue;
            } else {
                int buf = { 0 };
                if( ten(f, a, buf) ) {
                    printf( "hit %05d/%05d = %d\n", a, f, j );
                    result.push_back( pair<int,int>(a, f) );
                }
            }
        }
    }
    cout << "size: " << result.size() << "\n";
}

hit 76508/01234 = 62
hit 08659/01237 = 7
hit 86590/01237 = 70
hit 89064/01237 = 72
hit 65879/01243 = 53
...
hit 93702/46851 = 2
hit 96270/48135 = 2
hit 96702/48351 = 2
hit 97026/48513 = 2
hit 97032/48516 = 2
hit 97062/48531 = 2
hit 97230/48615 = 2
hit 97302/48651 = 2
size: 763

原答案似乎简洁很多：

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

int main() {
    int n, kase = 0;
    char buf;
    while( scanf( "%d", &n ) == 1 && n ) {
        int cnt = 0;
        if( kase++ ) { printf( "\n" ); }
        for( int fghij = 1234; ; fghij++ ) {
            int abcde = fghij * n;
            sprintf( buf, "%05d%05d", abcde, fghij );
            if( strlen( buf ) > 10 ) { break; }
            sort( buf, buf+10 );
            int ok = 1;
            for( int i = 0; i < 10; i++ ) {
                if( buf[i] != '0' + i ) { ok = 0; break; }
            }
            if( ok ) {
                cnt++;
                printf( "%05d / %05d = %d\n", abcde, fghij, n );
            }
        }
        if( !cnt ) { printf( "There are no solutions for %d.\n", n ); }
    }
    return 0;
}

最大乘积 @

这个存粹是暴力了起点和终点，然后看是否“水位更高”。

输入 n 个元素组成的序列 S，找一个乘积最大的连续子序列。如果最大为负，输出 0。1 <= n <= 18，-10 <= S_i <= 10。

input:

    3
    2   4  -3
    5
    2   5  -1   2  -1

output:

    8
    20

因为 n 和 S_i 的值域，最大乘积不会超过 10¹⁸，可以用 long long 表示。

// UVa11059 Maximum Product
#include <iostream>
using namespace std;

int main() {
    int S, kase = 0, n;
    while( cin >> n && n ) {
        for( int i = 0; i < n; i++ ) { cin >> S[i]; }
        long long ans = 0;
        for( int i = 0; i < n; i++ ) {
            long long v = 1;
            for( int j = i; j < n; j++ ) {
                v *= S[j];
                if( v > ans ) { ans = v; }
            }
        }
        cout << "Case #" << ++kase
             << ": The maximum product is " << ans << ".\n\n";
    }
    return 0;
}

分数拆分，Fractual Again? ♥️ @

暴力前分析了取值范围。

输入正整数 k，找到所有的正整数 x >= y，使得 1/k = 1/x + 1/y。

input:

    2
    12

output:

    2
    1/2 = 1/6 + 1/3
    1/2 = 1/4 + 1/4
    8
    1/12 = 1/156 + 1/13
    1/12 = 1/84 + 1/14
    1/12 = 1/60 + 1/15
    1/12 = 1/48 + 1/16
    1/12 = 1/36 + 1/18
    1/12 = 1/30 + 1/20
    1/12 = 1/28 + 1/21
    1/12 = 1/24 + 1/24

分析：

1/k = 1/x + 1/y
x >= y -> 1/x <= 1/y -> 1/k <= 2/y -> y <= 2k
x > 0 -> y > k

所以在 y~(k, 2k] 枚举。

// UVa10976 Fractions Again?!
#include <cstdio>
#include <vector>
using namespace std;

int main() {
    int k;
    while( scanf( "%d", &k ) == 1 && k ) {
        vector<int> X, Y;
        for( int y = k+1; y <= k*2; ++y ) {
            if( k*y%( y-k ) == 0 ) {                // 1/k = 1/x + 1/y => x = ky/(y-k)
                X.push_back(k*y/(y-k)); Y.push_back(y);
            }
        }
        printf( "%d\n", X.size() );
        for( int i = 0; i < X.size(); i++ ) {
            printf( "1/%d = 1/%d + 1/%d\n", k, X[i], Y[i] );
        }
    }
    return 0;
}

枚举排列 @

next_permutation ♥️ @

下面考虑用 C 语言实现。不难想到用数组表示 P 和 S。由于 P 和 S 是互补的，它们二者知道其中给一个，另一个就完全确定了，因此不用保存 P。

P    P    P    P    ...     P[cur]  ...     P[n-1]
|-------- used -------------------------|-----not used--------|

#include <cstdio>
#include <cstdlib>
#include <vector>

using namespace std;

// permutation P, set S
static void print_permutation_r( int n, int cur, int P[] ) {
    if( cur == n ) {                                            // 收敛条件
        for( int i = 0; i < n; ++i ) { printf( "%d", P[i] ); }
        printf( "\n" );
    }

    // 扩展状态，尝试在 A[cur] 中填各种整数 i，按从小到大的顺序
    for( int i = 1; i <= n; i++ ) {
        int used = 0;
        for( int j = 0; j < cur; j++ ) {
            if( P[j] == i ) { used = 1; break; }                // 如果 i 已经在 A~A[cur-1] 出现过，则不能再选
        }
        if( !used ) {
            P[cur] = i;
            print_permutation_r( n, cur + 1, P );               // 递归调用
        }
    }
}

int main() {
    int n;
    vector<int> P;
    while( scanf( "%d", &n ) && n ) {
        P.resize(n);
        print_permutation_r( n, 0, &P[0] );
    }
}

真的很像八皇后。

如果确定了 n 的范围，比如 n <= 100，可以用全局 A，避免动态内存分配。

Leetcode: Next Permutation @

处理步骤：
                            ^ increase
                             \
                              \
                               \
        <-----------------------\
            i   j   *   *   *   *

Example

            6   8   7   4   3   2
step 1     [6]  8   7   4   3   2
step 2      6   8  [7]  4   3   2
step 3      7   8   6   4   3   2
step 4      7  [8   6   4   3   2]
            7   2   2   4   6   8

1.  from right to left, find the first digit which violate the increase，这里是 6，称之为 PartitionNumber
2.  from right to left, find the first digit which large than PartitionNumber（6）,
    call it ChangeNumber，这里是 7。
3.  swap the PartitionNumber and ChangeNumber；
4.  Reverse all the digit on the right of partition index。

// 这里的 ROF 是 for 倒过来，意思就是 i 从 b 到 a。
#define ROF(i, a, b) for (int i = (b); --i >= (a); )

class Solution {
public:
    void nextPermutation(vector<int> &num) {
        if (num.size() <= 1) return;
        // ROF(i, 0, num.size()-1) {
        for( int i = num.size()-2; i >= 0; --i ) {
            if ( i+1 < num.size() && num[i] < num[i+1] ) {
                int j = num.size();
                while (! (num[i] < num[--j]));  // num[i] < num[j]
                swap(num[i], num[j]);
                reverse(num.begin()+i+1, num.end());
                return;
            }
        }
        reverse(num.begin(), num.end());
    }
};

refs and see also

Next Permutation | LeetCode OJ

Leetcode: Permutation Sequence @

The set [1,2,3,…,n] contains a total of n! unique permutations. 输入 n 和 k，返回第 k 个序列。

最无赖的解法：

class Solution {
public:
    string getPermutation(int n, int k) {
        string s(n, '0');
        for (int i = 0; i < n; ++i)
            s[i] += i+1;
        for (int i = 0; i < k-1; ++i)
            next_permutation(s.begin(), s.end());
        return s;
    }
};

这个方法可以得到答案，但是……Status: Time Limit Exceeded……

康托展开, Cantor expansion @

X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a[1]*0!，其中 a[i] 为当前未出现的元素中是排在第几个（从 0开始）。这就是康托展开。康托展开可用代码实现。

refs and see also

利用康托编码的思路，假设有 n 个不重复的元素，第 k 个排列是 a₁, a₂, a₃, …, a_n，那么 a₁ 是哪一个位置呢？我们把 a₁去掉，那么剩下的排列为 a₂, a₃, …, a_n, 共计 n-1 个元素，n-1 个元素共有 (n-1)! 个排列，于是就可以知道 a₁ = k / (n-1)!。

同理，a₂, a₃, …, a_n 的值推导如下：

k₂ = k%(n-1)!
a₂ = k₂/(n-2)!
…
k_n-1 = k_n-2%2!
a_n-1 = k_n-1%1!
a_n = 0

// 康托编码，时间复杂度 O(n)，空间复杂度 O(1)
class Solution {
public:
    string getPermutation(int n, int k) {
        string s(n, '0');
        string result;
        for (int i = 0; i < n; ++i)
            s[i] += i + 1;
        return kth_permutation(s, k);
    }
private:
    int factorial(int n) {
        int result = 1;
        for (int i = 1; i <= n; ++i)
            result *= i;
        return result;
    }

    template<typename Sequence>                                     // seq 已排好序，是第一个排列
    Sequence kth_permutation(const Sequence &seq, int k) {
        const int n = seq.size();
        Sequence S(seq), result;
        result.reserve( n );

        int base = factorial(n - 1);
        --k;                                                        // 康托编码从 0 开始

        for (int i = n - 1; i > 0; k %= base, base /= i, --i ) {    // base/=i 实在太巧妙
            auto a = next(S.begin(), k / base);
            result.push_back(*a);
            S.erase(a);                                             // 记得 erase 掉！
        }

        result.push_back(S[0]);                                     // 最后一个
        return result;
    }
};

上面那个答案通过了。下面有个更简洁的。也通过了。

#define ROF(i, a, b) for (int i = (b); --i >= (a); )

class Solution {
public:
    string getPermutation(int n, int k) {
        // factorial:   0     1   2   3    4      5       6        7        8
        int f[] =     { 1,    1,  2,  6,  24,   120,    720,    5040,   40320   };
        vector<bool> a(n, true);
        string r;
        k--;
        ROF(i, 0, n) {
            int t = k/f[i], j = 0;
            k %= f[i];
            while (!a[j]) j++;
            while (t--)
                while (! a[++j]);
            a[j] = false;
            r += '1'+j;
        }
        return r;
    }
};

refs and see also

Permutation Sequence | LeetCode OJ

生成可重集的排列 ♥️ @

直接用 STL 里面的 next_permutation @

std::next_permutation 接口 @

template< class BidirIt >
bool next_permutation( BidirIt first, BidirIt last );

template< class BidirIt, class Compare >
bool next_permutation( BidirIt first, BidirIt last, Compare comp );

Possible implementation ♥️ ♥️ @

template<class BidirIt>
bool next_permutation(BidirIt first, BidirIt last)
{
    if (first == last) return false;                // no element
    BidirIt i = last;
    if (first == --i) return false;                 // only one element

    while (true) {
        BidirIt i1, i2;

        i1 = i;
        if (*--i < *i1) {
            i2 = last;
            while (!(*i < *--i2))
                ;
            std::iter_swap(i, i2);                  // iter_swap?? TODO
            std::reverse(i1, last);
            return true;
        }
        if (i == first) {
            std::reverse(first, last);
            return false;                           // great! termination.
        }
    }
}

#include <stdio.h>
#include <stdlib.h>
#include <algorithm>

using namespace std;

int main() {
    int n, p;
    scanf( "%d", &n );
    for( int i = 0; i < n; i++ ) { scanf( "%d", &p[i] ); }
    sort( p, p+n );                                                 // 排序，得到 p 的最小排列
    do {
        for( int i = 0; i < n; i++ ) { printf( "%d ", p[i] ); }     // 输出排列 p
        printf( "\n" );
    } while(  next_permutation( p, p+n )  );                        // 求下一个排列
    return 0;
}

$ echo "4 5 2 2 4" | ./a.out
2 2 4 5
2 2 5 4
2 4 2 5
2 4 5 2
2 5 2 4
2 5 4 2
4 2 2 5
4 2 5 2
4 5 2 2
5 2 2 4
5 2 4 2
5 4 2 2

当然，自己写也是可以得。【这个代码十分重要！！！】♥️ @

#include <cstdio>
#include <algorithm>
using namespace std;

const int maxn = 50;
int P[maxn], A[maxn];

// 输出数组 P 中元素的全排列。数组 P 中可能有重复元素
void print_permutation( int n, int *P, int *A, int cur ) {
    if( cur == n ) {
        for( int i = 0; i < n; i++ ) { printf( "%d ", A[i] ); } printf( "\n" );
    } else {
        for( int i = 0; i < n; i++ ) {
            if( i == 0 || P[i] != P[i-1] ) {
                int c1 = 0, c2 = 0;
                for( int j = 0; j < cur; j++ ) { if( A[j] == P[i] ) { c1++; } }
                for( int j = 0; j <   n; j++ ) { if( P[i] == P[j] ) { c2++; } }
                if( c1 < c2 ) {
                    A[cur] = P[i];
                    print_permutation( n, P, A, cur+1 );
                }
            }
        }
    }
}

int main() {
    int i, n;
    scanf( "%d", &n );
    for( i = 0; i < n; i++ ) {
        scanf( "%d", &P[i] );
    }
    sort( P, P+n );
    print_permutation( n, P, A, 0 );
    return 0;
}

$ echo 4 2 3 1 1 | ./a.out
1 1 2 3
1 1 3 2
1 2 1 3
1 2 3 1
1 3 1 2
1 3 2 1
2 1 1 3
2 1 3 1
2 3 1 1
3 1 1 2
3 1 2 1
3 2 1 1

所以啊，枚举排列要不自己递归枚举，要不就用 stl 的 next_permutation。

解答树 @

                                                            (*,*,*,*)
                                                                |
              .--------------------------------+----------------+---------------+-------------------------------.
              |                                |                                |                               |
          (1,*,*,*)                        (2,*,*,*)                        (3,*,*,*)                       (4,*,*,*)
         /    |    \                      /    |    \                      /    |    \                     /    |    \
(1,2,*,*) (1,3,*,*) (1,4,*,*)    (2,1,*,*) (2,3,*,*) (2,4,*,*)    (3,1,*,*) (3,2,*,*) (3,4,*,*)   (4,1,*,*) (4,2,*,*) (4,3,*,*)

第 0 层有 n 个儿子，第一层各节点各有 n-1 个儿子，第二层各有 n-2 个儿子，第 n 层节点没有儿子。每个叶子对应一个排列，共有 n! 个叶子。这棵树展示的是：从什么都没做到逐步生成完整解的过程。

解答树特点: 多步骤，多选择，用递归

0 层：1 个节点，1 层：n 个节点，2 层：n*(n-1)，第 3 层：n*(n-1)*(n-2)，第 n 层：n*(n-1)*(n-2)*(n-3)*...*1 = n! 个节点。全部加起来。最后居然复杂度是 O(n!)　TODO（把公式写完整）

多数情况下: 解答树上所有节点来源于最后一两层

1 + 1/2 + 1/3 + … = e，泰勒公式。

子集生成 @

增量构造法 @

// {0~n-1} 的所有子集：增量构造法
#include <cstdio>
using namespace std;

void print_subset( int n, int* A, int cur ) {
    for( int i = 0; i < cur; i++ ) { printf( "%d ", A[i] ); }   // 打印当前集合
    printf( "\n" );
    int s = cur != 0 ? A[cur-1]+1 : 0;                          // 确定当前元素的最小可能值
    for( int i = s; i < n; i++ ) {
        A[cur] = i;
        print_subset( n, A, cur+1 );                            // 递归构造子集
    }
}

int A;
int main() {
    int n;
    scanf( "%d", &n );
    print_subset( n, A, 0 );
    return 0;
}

output

位向量法 @

不直接构造 A，取而代之构造 B。

开一个位向量 B，B[i]=1 表示选择 S[i], B[i]=0 表示不选择。

// {0~n-1} 的所有子集：位向量法
#include <cstdio>
using namespace std;

void print_subset( int n, int* B, int cur ) {
    if( cur == n ) {
        for( int i = 0; i < cur; i++ ) {
            if( B[i] ) { printf( "%d ", i ); }      // 打印当前集合
        }
        printf( "\n" );
        return;
    }
    B[cur] = 1;                                     // 选第 cur 个元素
    print_subset( n, B, cur+1 );
    B[cur] = 0;                                     // 不选第 cur 个元素
    print_subset( n, B, cur+1 );
}

int B;
int main() {
    int n;
    scanf( "%d", &n );
    for( int i = 0; i < n; ++i ) { scanf("%d", &B[i]); }
    print_subset( n, B, 0 );
    return 0;
}

二进制法 @

前提：集合的元素不超过 int 位数。用一个 int 整数表示位向量，第 i 位为 1，则表示选择 S[i]，为 0 则不选择。例如 S={A,B,C,D}，则 0110=6 表示子集 {B,C}。

这种方法最巧妙。因为它不仅能生成子集，还能方便的表示集合的并、交、差等集合运算。设两个集合的位向量分别为 B1 和 B2，则 B1|B2, B1&B2, B1^B2 分别对应集合的并、交、对称差。

15  14  13  12  11  10  9   8   7   6   5   4   3   2   1   0
|   |   |   |   |   |   |   |   |   |   |   |   |   |   |   |
0   1   0   0   0   1   1   0   0   0   1   1   0   1   1   1
    ^               ^   ^               ^   ^       ^   ^   ^
    |               |   |               |   |       |   |   |
    +---------------+---+---------------+---+-------+---+---+
                        |
                        |
                        V
           { 14, 10, 9, 5, 4, 2, 1, 0 }

XOR 最重要的性质是“开关性” — XOR 两次等于没有 XOR：A^BB = A。

// {0~n-1}的所有子集：二进制法
#include <cstdio>
using namespace std;

void print_subset( int n, int s ) {             // 打印 {0, 1, 2, ..., n-1} 的子集 S
    for( int i = 0; i < n; i++ ) {
        if( s&(1<<i) ) { printf("%d ", i); }    // 这里利用了 C 语言“非 0 值都为真”的规定
    }
    printf( "\n" );
}

int main() {
    int n;
    scanf( "%d", &n );
    for( int i = 0; i < ( 1<<n ); i++ ) {       // 枚举各子集所对应的编码 0, 1, 2, ..., 2^n-1
        print_subset( n, i );
    }
    return 0;
}

$ echo 3 | ./a.out
0
1
0 1
2
0 2
1 2
0 1 2

ALL_BITS = (1<<n) -1，A 的补集就是 A^ALL_BITS。

回溯法 @

回溯法理论 TODO @

之前两种思路是：递归构造、直接枚举（generate，然后 test）。

n 皇后问题 @

问题描述 @
The eight queens puzzle is the problem of placing eight chess queens on an 8×8 chessboard so that no two queens threaten each other. Thus, a solution requires that no two queens share the same row, column, or diagonal. The eight queens puzzle is an example of the more general n queens problem of placing n non-attacking queens on an n×n chessboard, for which solutions exist for all natural numbers n with the exception of n=2 and n=3.

The eight queens puzzle has 92 distinct solutions. If solutions that differ only by symmetry operations (rotations and reflections) of the board are counted as one, the puzzle has 12 fundamental solutions.

refs and see also
- Eight queens puzzle - Wikipedia, the free encyclopedia

生成 - 测试法 @

generate-test，也就是直接枚举法（暴力法）。

These brute-force algorithms to count the number of solutions are computationally manageable for n = 8, but would be intractable for problems of n ≥ 20, as 20! = 2.433 x 10¹⁸.

// n 皇后问题：生成-测试法
#include <cstdio>
using namespace std;

int C, tot = 0, n = 8, nc = 0;

void search( int cur ) {
    int i, j;
    nc++;
    if( cur == n ) {
        for( i = 0; i < n; i++ ) {      // 到最后再判断咯。是否 valid
            for(j = i+1; j < n; j++) {
                if( C[i] == C[j] || i-C[i] == j-C[j] || i+C[i] == j+C[j] ) { return; }
            }
        }
        tot++;
    } else for( i = 0; i < n; i++ ) {
        C[cur] = i;                     // 直接暴力很多情况，很多都是不可行的
        search( cur+1 );
    }
}

int main() {
    scanf( "%d", &n );
    search( 0 );
    printf( "%d\n", tot );
    printf( "%d\n", nc );
    return 0;
}

$ echo 8 | ./a.out
92
19173961

普通回溯法 @

// n 皇后问题：普通回溯法
#include <cstdio>
using namespace std;

int C, tot = 0, n = 8, nc = 0;

void search( int cur ) {
    int i, j;
    nc++;
    if( cur == n ) {
        tot++;
    } else for( i = 0; i < n; i++ ) {
        int ok = 1;
        C[cur] = i;
        for( j = 0; j < cur; j++ ) {        // 在进入一种可能性的时候就判断是否可能。
            int dx = cur - j, dy = C[cur] - C[j];
            if( C[cur] == C[j] || dx == dy || dy == -dy ) {
                ok = 0;
                break;
            }
        }
        if( ok ) { search( cur+1 ); }
    }
}

int main() {
    scanf( "%d", &n );
    search( 0 );
    printf( "%d\n", tot );
    printf( "%d\n", nc );
    return 0;
}

$ echo 8 | ./a.out
92
2057        # 对比直接暴力法的 19173961

优化了的回溯法 @

通过设置标志位来避免通过循环来判断是否 valid。

  y - x    ?dx == dy                                y + x    ? dx == -dy (dx+dy==0)
      +----------------------------------> y            +-----------------------------------> y
      |  0   1   2   3   4   5   6   7                  |  0   1   2   3   4   5   6   7
      | -1   0   1   2   3   4   5   6                  |  1   2   3   4   5   6   7   8
      | -2  -1   0   1   2   3   4   5                  |  2   3   4   5   6   7   8   9
      | -3  -2  -1   0   1   2   3   4                  |  3   4   5   6   7   8   9  10
      | -4  -3  -2  -1   0   1   2   3                  |  4   5   6   7   8   9  10  11
      | -5  -4  -3  -2  -1   0   1   2                  |  5   6   7   8   9  10  11  12
    x | -6  -5  -4  -3  -2  -1   0   1               x  |  6   7   8   9  10  11  12  13
      | -7  -6  -5  -4  -3  -2  -1   0                  |  7   8   9  10  11  12  13  14
      V                                                 V

标志位的编码无所谓，只要能检测标志、设置标志、移除标志，即可。

这个在我的一个简历投递里说得还详细点：应聘简答 for 创业公司求 Java 开发工程师，基于微信平台。 @

首先不能同行，那就直接用 C[i]（i=[0,7)，每个 i 都不一样）来存储每一行的列的位置。比如 C[2]=5 代表皇后点位为 (3, 6)。

不能同列，可以用循环检测是否和其他皇后冲突。

不能同斜线，可以用循环检测是否和其他皇后冲突。两种情况：

dx == dy
dx == -dy

优化 1：把 8 皇后的放置看成一个过程，第一个皇后，随意放，第二个皇后，只要和第一个皇后不冲突，随意放，以此，八个皇后都放上了，就是一个 valid 的情况。

这样冲突的判断不必要和全部其他皇后检测，只需要看之前的皇后。

优化 2：列、主对角线、副对角线编码，存起来，占了一个坑，就把那个坑标记好。

这样，就不用通过循环来判断是否冲突了。只要检测一个标志位。

这个标志位设计方案怎么都可以，比如像这样：

    主对角线                                            副对角线

  y - x    ?dx == dy                                y + x    ? dx == -dy (dx+dy==0)
      +----------------------------------> y            +-----------------------------------> y
      |  0   1   2   3   4   5   6   7                  |  0   1   2   3   4   5   6   7
      | -1   0   1   2   3   4   5   6                  |  1   2   3   4   5   6   7   8
      | -2  -1   0   1   2   3   4   5                  |  2   3   4   5   6   7   8   9
      | -3  -2  -1   0   1   2   3   4                  |  3   4   5   6   7   8   9  10
      | -4  -3  -2  -1   0   1   2   3                  |  4   5   6   7   8   9  10  11
      | -5  -4  -3  -2  -1   0   1   2                  |  5   6   7   8   9  10  11  12
    x | -6  -5  -4  -3  -2  -1   0   1               x  |  6   7   8   9  10  11  12  13
      | -7  -6  -5  -4  -3  -2  -1   0                  |  7   8   9  10  11  12  13  14
      V                                                 V

代码如下：

void search( int cur ) {
    if( cur == n ) {
        ++tot;
        // 打印结果的代码放在这里
    } else {
        for( int i = 0; i < n; ++i ) {
            // vis: visited, vis[0] -> col, vis[1] -> minor diag, vis[2] -> major diag
            if( !vis[0][i] && !vis[1][cur+i] && !vis[2][cur-i+n] ) {
                C[cur] = i;
                // col         y-x=0           y+x=0
                vis[0][i] = vis[1][cur+i] = vis[2][cur-i+n] = 1;
                search( cur+1 );
                vis[0][i] = vis[1][cur+i] = vis[2][cur-i+n] = 0;    // 改回来
            }
        }
    }
}

其中 vis 是一个二维数组，vis[0][i] 表示第 i 列是否被占坑（1 是有人，0 是没人）， vis[1][i] 表示副对角线（上面右图）， vis[2][i] 表示主对角线（上面左图，因为 cur-i 可能为负（图中下三角部分），所以，要加上 n=8 ）。

如果想看看每个可能情况的放置，在上面 // 打印结果的代码放在这里 处加上：

printf( "solve #%d:", tot );
for( int i = 0; i < n; ++i ) {
    printf( " %d", C[i] );
}
printf( "\n" );

输出如下：

solve #1: 0 4 7 5 2 6 1 3
solve #2: 0 5 7 2 6 3 1 4
solve #3: 0 6 3 5 7 1 4 2
solve #4: 0 6 4 7 1 3 5 2
...
solve #89: 7 1 3 0 6 4 2 5
solve #90: 7 1 4 2 0 6 3 5
solve #91: 7 2 0 5 1 4 6 3
solve #92: 7 3 0 2 5 1 6 4

或者，你要一个视觉化的表示，上面的代码可以这么来：

printf( "-- Solve #%03d --\n", tot );
for( int i = 0; i < n; ++i ) {
    printf( "+-+-+-+-+-+-+-+-+\n" );
    for( int j = 0; j < n; ++j ) {
        printf( "|%c", C[i] == j ? 'X' : ' ' );
    }
    printf( "|\n" );
}
printf( "-----------------\n\n" );

打印出来就是这样：（如果看得不够“方”，那是字宽和行高的问题，就怪不得我了）

-- Solve #092 --
+-+-+-+-+-+-+-+-+
| | | | | | | |X|
+-+-+-+-+-+-+-+-+
| | | |X| | | | |
+-+-+-+-+-+-+-+-+
|X| | | | | | | |
+-+-+-+-+-+-+-+-+
| | |X| | | | | |
+-+-+-+-+-+-+-+-+
| | | | | |X| | |
+-+-+-+-+-+-+-+-+
| |X| | | | | | |
+-+-+-+-+-+-+-+-+
| | | | | | |X| |
+-+-+-+-+-+-+-+-+
| | | | |X| | | |
-----------------

#include <cstdio>
#include <cstring>
using namespace std;

int vis, C, tot = 0, n = 8, nc = 0;

void search( int cur ) {
    ++nc;
    if( cur == n ) {
        ++tot;
    } else {
        for( int i = 0; i < n; ++i ) {
            // vis: visited, vis -> col, vis -> minor diag, vis -> major diag
            if( !vis[i] && !vis[cur+i] && !vis[cur-i+n] ) {
                C[cur] = i;
                // col          x+y                 y-x
                vis[i] = vis[cur+i] = vis[cur-i+n] = 1;
                search( cur+1 );
                vis[i] = vis[cur+i] = vis[cur-i+n] = 0;    // 改回来
            }
        }
    }
}

int main() {
    memset( vis, 0, sizeof(vis) );
    search( 0 );
    printf( "%d\n", tot );
    printf( "%d\n", nc );
    return 0;
}

output:

92
2057

print the result:

++tot;
// add several lines here
printf( "solve #%d:", tot );
for( int i = 0; i < n; ++i ) {
    printf( " %d", C[i] );
}
printf( "\n" );

see all the 92 solves. @

solve #1: 0 4 7 5 2 6 1 3
solve #2: 0 5 7 2 6 3 1 4
solve #3: 0 6 3 5 7 1 4 2
solve #4: 0 6 4 7 1 3 5 2
solve #5: 1 3 5 7 2 0 6 4
solve #6: 1 4 6 0 2 7 5 3
solve #7: 1 4 6 3 0 7 5 2
solve #8: 1 5 0 6 3 7 2 4
solve #9: 1 5 7 2 0 3 6 4
solve #10: 1 6 2 5 7 4 0 3
solve #11: 1 6 4 7 0 3 5 2
solve #12: 1 7 5 0 2 4 6 3
solve #13: 2 0 6 4 7 1 3 5
solve #14: 2 4 1 7 0 6 3 5
solve #15: 2 4 1 7 5 3 6 0
solve #16: 2 4 6 0 3 1 7 5
solve #17: 2 4 7 3 0 6 1 5
solve #18: 2 5 1 4 7 0 6 3
solve #19: 2 5 1 6 0 3 7 4
solve #20: 2 5 1 6 4 0 7 3
solve #21: 2 5 3 0 7 4 6 1
solve #22: 2 5 3 1 7 4 6 0
solve #23: 2 5 7 0 3 6 4 1
solve #24: 2 5 7 0 4 6 1 3
solve #25: 2 5 7 1 3 0 6 4
solve #26: 2 6 1 7 4 0 3 5
solve #27: 2 6 1 7 5 3 0 4
solve #28: 2 7 3 6 0 5 1 4
solve #29: 3 0 4 7 1 6 2 5
solve #30: 3 0 4 7 5 2 6 1
solve #31: 3 1 4 7 5 0 2 6
solve #32: 3 1 6 2 5 7 0 4
solve #33: 3 1 6 2 5 7 4 0
solve #34: 3 1 6 4 0 7 5 2
solve #35: 3 1 7 4 6 0 2 5
solve #36: 3 1 7 5 0 2 4 6
solve #37: 3 5 0 4 1 7 2 6
solve #38: 3 5 7 1 6 0 2 4
solve #39: 3 5 7 2 0 6 4 1
solve #40: 3 6 0 7 4 1 5 2
solve #41: 3 6 2 7 1 4 0 5
solve #42: 3 6 4 1 5 0 2 7
solve #43: 3 6 4 2 0 5 7 1
solve #44: 3 7 0 2 5 1 6 4
solve #45: 3 7 0 4 6 1 5 2
solve #46: 3 7 4 2 0 6 1 5
solve #47: 4 0 3 5 7 1 6 2
solve #48: 4 0 7 3 1 6 2 5
solve #49: 4 0 7 5 2 6 1 3
solve #50: 4 1 3 5 7 2 0 6
solve #51: 4 1 3 6 2 7 5 0
solve #52: 4 1 5 0 6 3 7 2
solve #53: 4 1 7 0 3 6 2 5
solve #54: 4 2 0 5 7 1 3 6
solve #55: 4 2 0 6 1 7 5 3
solve #56: 4 2 7 3 6 0 5 1
solve #57: 4 6 0 2 7 5 3 1
solve #58: 4 6 0 3 1 7 5 2
solve #59: 4 6 1 3 7 0 2 5
solve #60: 4 6 1 5 2 0 3 7
solve #61: 4 6 1 5 2 0 7 3
solve #62: 4 6 3 0 2 7 5 1
solve #63: 4 7 3 0 2 5 1 6
solve #64: 4 7 3 0 6 1 5 2
solve #65: 5 0 4 1 7 2 6 3
solve #66: 5 1 6 0 2 4 7 3
solve #67: 5 1 6 0 3 7 4 2
solve #68: 5 2 0 6 4 7 1 3
solve #69: 5 2 0 7 3 1 6 4
solve #70: 5 2 0 7 4 1 3 6
solve #71: 5 2 4 6 0 3 1 7
solve #72: 5 2 4 7 0 3 1 6
solve #73: 5 2 6 1 3 7 0 4
solve #74: 5 2 6 1 7 4 0 3
solve #75: 5 2 6 3 0 7 1 4
solve #76: 5 3 0 4 7 1 6 2
solve #77: 5 3 1 7 4 6 0 2
solve #78: 5 3 6 0 2 4 1 7
solve #79: 5 3 6 0 7 1 4 2
solve #80: 5 7 1 3 0 6 4 2
solve #81: 6 0 2 7 5 3 1 4
solve #82: 6 1 3 0 7 4 2 5
solve #83: 6 1 5 2 0 3 7 4
solve #84: 6 2 0 5 7 4 1 3
solve #85: 6 2 7 1 4 0 5 3
solve #86: 6 3 1 4 7 0 2 5
solve #87: 6 3 1 7 5 0 2 4
solve #88: 6 4 2 0 5 7 1 3
solve #89: 7 1 3 0 6 4 2 5
solve #90: 7 1 4 2 0 6 3 5
solve #91: 7 2 0 5 1 4 6 3
solve #92: 7 3 0 2 5 1 6 4
92

we can also print out the details:

printf( "-- Solve #%03d --\n", tot );
for( int i = 0; i < n; ++i ) {
    printf( "+-+-+-+-+-+-+-+-+\n" );
    for( int j = 0; j < n; ++j ) {
        printf( "|%c", C[i] == j ? 'X' : ' ' );
    }
    printf( "|\n" );
}
printf( "-----------------\n\n" );

which yields to:

-- Solve #092 --
+-+-+-+-+-+-+-+-+
| | | | | | | |X|
+-+-+-+-+-+-+-+-+
| | | |X| | | | |
+-+-+-+-+-+-+-+-+
|X| | | | | | | |
+-+-+-+-+-+-+-+-+
| | |X| | | | | |
+-+-+-+-+-+-+-+-+
| | | | | |X| | |
+-+-+-+-+-+-+-+-+
| |X| | | | | | |
+-+-+-+-+-+-+-+-+
| | | | | | |X| |
+-+-+-+-+-+-+-+-+
| | | | |X| | | |
-----------------

prime ring @

输入正整数 n，把整数 1，2，…，n 组成一个环，使得相邻两个整数的和均为素数。输出时从整数 1 开始逆时针排列。同一个环应恰好输出一次。n <= 16。

input:

    6

output:

    1   4   3   2   5   6
    1   6   5   2   3   4

如果直接暴力。排列总数高达 16! = 2x10¹³ @

直接暴力–生成测试法。

for( int i = 2; i <= n*2; ++i ) { isp[i] = is_prime( i ); }
for( int i = 0; i < n; ++i ) { A[i] = i+1; }
do  {
    int ok = 1;
    for( int i = 0; i < n; ++i ) {
        if( !isp[A[i]+A[(i+1)%n]] ) { ok = 0; break; }
    }
    if( ok ) {
        for( int i = 0; i < n; ++i ) { printf( "%d ", A[i] ); }
        printf( "\n" );
    }
} while( next_permutation(A+1, A+n) );

当 n = 12 就相当慢了。

生成–测试法太慢，现在用回溯法 @

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

int is_prime( int x ) {
    for( int i = 2; i*i <= x; i++ ) {
        if( x % i == 0 ) { return 0; }
    }
    return 1;
}

const int maxn = 50;
int n, A[maxn], isp[maxn], vis[maxn];
void dfs( int cur ) {
    if( cur == n && isp[A[0]+A[n-1]] ) {                // 已经处理了所有，除了第一个和最后一个（闭环）
        for( int i = 0; i < n; i++ ) {
            if( i != 0 ) { printf( " " ); }
            printf( "%d", A[i] );
        }
        printf( "\n" );
    } else {
        for( int i = 2; i <= n; i++ ) {
            if( !vis[i] && isp[i+A[cur-1]] ) {          // 这次我选 i，设置 cur 的位置
                A[cur] = i;
                vis[i] = 1;                             // visited
                dfs( cur+1 );                           // 递归，处理 cur+1 的位置
                vis[i] = 0;                             // change back
            }
        }
    }
}

int main() {
    int kase = 0;
    for( int i = 0; i < maxn; ++i ) { isp[i] = is_prime( i ); }
    while( scanf( "%d", &n ) == 1 && n > 0 ) {
        if( kase > 0 ) { printf( "\n" ); }
        printf( "Case %d:\n", ++kase );
        memset( vis, 0, sizeof(vis) );
        A[0] = 1;
        dfs( 1 );   // put A[1]
    }
    return 0;
}

$ echo 6 | ./a.out
Case 1:
1 4 3 2 5 6
1 6 5 2 3 4

因为是一个环，所以固定了第一个是 1。这样便没有重复输出。里面的 i 也是从 2 开始循环，所以不用担心 vis[1] 没有设定了。

困难的串 Krypton Factor :???: @

包含两个相邻的重复子串，称之为“容易的串”，否则，“困难的串”。例如，“BB”、“ABCDACABCAB”、“ABCDABCD”都是容易的，而“D”、“DC”、“ABDAB”、“CBABCBA”都是困难的串。

输入正整数 n 和 L，输出由钱 L 个字符组成的、字典序第 k 小的困难的串。

input:

    7   3
    30  3

output:

    ABAC ABA
    ABAC ABCA CBAB CABA CABC ACBA CABA

// UVa129 Krypton Factor
#include <stdio.h>
int n, L, cnt;
int S;

int dfs( int cur ) {                                                // 返回 0 表示已经得到解，无须继续搜索
    if( cnt++ == n ) {
        for( int i = 0; i < cur; i++ ) {
            if( i % 64 == 0 && i > 0 ) {
                printf( "\n" );
            } else if( i % 4 == 0 && i > 0 ) {
                printf( " " );
            }
            printf( "%c", 'A'+S[i] );                               // 输出方案
        }
        printf( "\n%d\n", cur );
        return 0;
    }
    for( int i = 0; i < L; i++ ) {
        S[cur] = i;
        int ok = 1;
        for( int j = 1; j*2 <= cur+1; j++ ) {                       // 尝试长度为 j*2 的后缀
            int equal = 1;
            for( int k = 0; k < j; k++ ) {                          // 检查后一半是否等于前一半
                if( S[cur-k] != S[cur-k-j] ) { equal = 0; break; }
            }
            if( equal ) { ok = 0; break; }                          // 后一半等于前一半，方案不合法
        }
        if( ok ) if( !dfs(cur+1) ) { return 0; }                    // 递归搜索。如果已经找到解，则直接退出
    }
    return 1;
}

int main() {
    while( scanf( "%d%d", &n, &L ) == 2 && n > 0 ) {
        cnt = 0;
        dfs( 0 );
    }
    return 0;
}

$ echo 7 3 | ./a.out
ABAC ABA
7

回溯法要注意忽略不必要的判断。

带宽，Bandwith ♥️ @

最优性剪纸

给出一个 n（n<=8）个节点的图 G 和一个节点的排列。定义节点 i 的带宽 b(i) 为 i 和相邻结点在排列中的最远距离，而所有 b(i) 的最大值就是整个图的带宽。给定图 G，求出让带宽最小的节点排列，如图 7-7 所示。

            A ------------- F
           /               /|
          /               / |
         /               /  H
        B ------------- G   |
        |               |   E
        |               |  /
        |               | /
        C-------------- D

            图 G

下面两个排列的带宽分别为 6 和 5。具体说，下面左图的各个结点的带宽分别为 6，6，1，4，1，1，6，6，右图的各个结点的带宽分别为 5，3，1，4，3，5，1，4。

    +-----------------------+         +-------------------+
    |                       |         |                   |
+-----------------------+   |         |   +-----------+   |
|   |                   |   |         |   |           |   |
|   |                   |   |         |   |           |   |
A   B   C   D   E   H   F   G         A   B   C   D   G   F   H   E
            |               |                     |               |
            |               |                     |               |
            +---------------+                     +---------------+

            (a)                                 (b)

// UVa140 Bandwidth
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;

const int maxn = 10;
int id, letter[maxn];

int main() {
    char input;
    while(scanf("%s", input) == 1 && input != '#') {
        // 计算结点个数并给字母编号
        int n = 0;
        for(char ch = 'A'; ch <= 'Z'; ch++)
            if(strchr(input, ch) != NULL) {
                id[ch] = n++;
                letter[id[ch]] = ch;
            }

        // 处理输入
        int len = strlen(input), p = 0, q = 0;
        vector<int> u, v;
        for(;;) {
            while(p < len && input[p] != ':') p++;
            if(p == len) break;
            while(q < len && input[q] != ';') q++;
            for(int i = p+1; i < q; i++) {
                u.push_back(id[input[p-1]]);
                v.push_back(id[input[i]]);
            }
            p++; q++;
        }

        // 枚举全排列
        int P[maxn], bestP[maxn], pos[maxn], ans = n;
        for(int i = 0; i < n; i++) P[i] = i;
        do {
            for(int i = 0; i < n; i++) pos[P[i]] = i; // 每个字母的位置
            int bandwidth = 0;
            for(int i = 0; i < u.size(); i++)
                bandwidth = max(bandwidth, abs(pos[u[i]] - pos[v[i]])); // 计算带宽
            if(bandwidth < ans) {
                ans = bandwidth;
                memcpy(bestP, P, sizeof(P));
            }
        } while(next_permutation(P, P+n));

        // 输出
        for(int i = 0; i < n; i++) printf("%c ", letter[bestP[i]]);
        printf("-> %d\n", ans);
    }
    return 0;
}

天平难题，Mobile Computing @

// UVa1354 Mobile Computing
// Rujia Liu
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;

struct Tree {
    double L, R; // distance from the root to the leftmost/rightmost point
    Tree():L(0),R(0) {}
};

const int maxn = 6;

int n, vis[1<<maxn];
double r, w[maxn], sum[1<<maxn];
vector<Tree> tree[1<<maxn];

void dfs(int subset) {
    if(vis[subset]) return;
    vis[subset] = true;

    bool have_children = false;
    for(int left = (subset-1)&subset; left; left = (left-1)&subset) {
        have_children = true;

        int right = subset^left;
        double d1 = sum[right] / sum[subset];
        double d2 = sum[left] / sum[subset];

        dfs(left); dfs(right);

        for(int i = 0; i < tree[left].size(); i++)
            for(int j = 0; j < tree[right].size(); j++) {
                Tree t;
                t.L = max(tree[left][i].L + d1, tree[right][j].L - d2);
                t.R = max(tree[right][j].R + d2, tree[left][i].R - d1);
                if(t.L + t.R < r) tree[subset].push_back(t);
            }
    }

    if(!have_children) tree[subset].push_back(Tree());
}

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        scanf("%lf%d", &r, &n);
        for(int i = 0; i < n; i++) scanf("%lf", &w[i]);
        for(int i = 0; i < (1<<n); i++) {
            sum[i] = 0;
            tree[i].clear();
            for(int j = 0; j < n; j++)
                if(i & (1<<j)) sum[i] += w[j];
        }

        int root = (1<<n)-1;
        memset(vis, 0, sizeof(vis));
        dfs(root);

        double ans = -1;
        for(int i = 0; i < tree[root].size(); i++)
            ans = max(ans, tree[root][i].L + tree[root][i].R);
        printf("%.10lf\n", ans);
    }
    return 0;
}

路径寻找问题 ♥️ @

八数码问题 ♥️ @

+---+---+---+        +---+---+---+
| 2 | 6 | 4 |        | 8 | 1 | 5 |
+---+---+---+        +---+---+---+
| 1 | 3 | 7 |        | 7 | 3 | 6 |
+---+---+---+        +---+---+---+
|   | 5 | 8 |        | 4 |   | 2 |
+---+---+---+        +---+---+---+

input: (current, goal)

    2   6   4   1   3   7   0   5   8
    8   1   5   7   3   6   4   0   2

output: (#steps)

    31

三种编码方式：

完美哈希：把 0~8 的全排列和 0~362879 对应起来。
hash 表：冲突越多效率越低，适用返回广。
STL 里的 set：set.insert( item )，set.count( item )，set.clear()

可以先用 set 把逻辑调通，然后换效率更高的 hash。

#include <iostream>
#include <algorithm>                                    // next_permutation
#include <stdio.h>
#include <string.h>
#include <math.h>                                       // sqrt

using namespace std;

typedef int State;
const int maxstate = 100000;

State st[maxstate], goal;
// int goal;
int dist[maxstate];

const int dx[] = {  -1,  1,  0,  0  };
const int dy[] = {   0,  0, -1,  1  };

int vis, fact;
void init_lookup_table() {                              // fact[i] = i!
    fact = 1;
    for( int i = 1; i < 9; ++i ) {
        fact[i] = fact[i-1] * i;
    }
}

int try_to_insert( int s ) {
    int code = 0;
    for( int i = 0; i < 9; ++i ) {
        int cnt = 0;
        for( int j = i+1; j < 9; ++j ) {
            if( st[s][j] < st[s][i] ) {
                ++cnt;
            }
        }
        code += fact[8-i] * cnt;
    }
    if( vis[code] ) {
        return 0;
    } else {
        return vis[code] = 1;
    }
}

int bfs() {
    init_lookup_table();
    int front = 1, rear = 2;                                    // 不适用下标 0，0 is 'not exist'
    while( front < rear ) {
        State &s = st[front];
        if( memcmp( goal, s, sizeof(s) ) == 0 ) {
            return front;                                       // gotcha
        }
        int z;
        for( z = 0; z < 9; ++z ) { if( !s[z] ) { break; } }     // get '0'
        int x = z/3, y = z%3;
        for( int d = 0; d < 4; ++d ) {
            int newx = x + dx[d];
            int newy = y + dy[d];
            int newz = newx * 3 + newy;
            if( newx >= 0 && newx < 3 && newy >= 0 && newy < 3 ) {
                State &t = st[rear];
                // seems, both `&t' or `t' will work
                memcpy( t, s, sizeof(s) );                      // type of t, s: int is actually a int *
                t[newz] = s[z];
                t[z] = s[newz];
                dist[rear] = dist[front] + 1;
                if( try_to_insert(rear) ) {
                    ++rear;
                }
            }
        }
        ++front;
    }
    return 0;
}

int main() {
    for( int i = 0; i < 9; ++i ) { scanf( "%d", &st[i] ); }
    for( int i = 0; i < 9; ++i ) { scanf( "%d", &goal[i] ); }
    int ans = bfs();
    if( ans > 0 ) {
        printf( "%d\n", dist[ans] );
    } else {
        printf( "-1\n" );
    }
    return 0;
}

input.txt

2   6   4   1   3   7   0   5   8
8   1   5   7   3   6   4   0   2

run it:

$ g++ source.cpp -o source
$ cat input.txt | ./source
1   2   3   4   5   6   7   8   0
1   2   3   4   5   6   8   7   0

完美哈希。

7-8 倒水问题，fill :???: @

三个杯子容量为 a，b，c（1<=a,b,c<=200）。

状态：第 1、2、3 杯子对应的水有 (v0, v1, v2)。

状态和它的转移：状态图（state graph）。

// UVa10603 Fill
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;

struct Node {
    int v[3], dist;
    bool operator < (const Node& rhs) const {
        return dist > rhs.dist;
    }
};

const int maxn = 200 + 5;
int mark[maxn][maxn], dist[maxn][maxn], cap[3], ans[maxn];

void update_ans(const Node& u) {
    for(int i = 0; i < 3; i++) {
        int d = u.v[i];
        if(ans[d] < 0 || u.dist < ans[d]) ans[d] = u.dist;
    }
}

void solve(int a, int b, int c, int d) {
    cap[0] = a; cap[1] = b; cap[2] = c;
    memset(ans, -1, sizeof(ans));
    memset(mark, 0, sizeof(mark));
    memset(dist, -1, sizeof(dist));
    priority_queue<Node> q;

    Node start;
    start.dist = 0;
    start.v[0] = 0; start.v[1] = 0; start.v[2] = c;
    q.push(start);

    dist = 0;
    while(!q.empty()) {
        Node u = q.top(); q.pop();
        if(mark[u.v][u.v]) continue;
        mark[u.v][u.v] = 1;
        update_ans(u);
        if(ans[d] >= 0) break;
        for(int i = 0; i < 3; i++)
            for(int j = 0; j < 3; j++) if(i != j) {
                if(u.v[i] == 0 || u.v[j] == cap[j]) continue;
                int amount = min(cap[j], u.v[i] + u.v[j]) - u.v[j];
                Node u2;
                memcpy(&u2, &u, sizeof(u));
                u2.dist = u.dist + amount;
                u2.v[i] -= amount;
                u2.v[j] += amount;
                int& D = dist[u2.v][u2.v];
                if(D < 0 || u2.dist < D){
                    D = u2.dist;
                    q.push(u2);
                }
            }
    }
    while(d >= 0) {
        if(ans[d] >= 0) {
            printf("%d %d\n", ans[d], d);
            return;
        }
        d--;
    }
}

int main() {
    int T, a, b, c, d;
    scanf("%d", &T);
    while(T--) {
        scanf("%d%d%d%d", &a, &b, &c, &d);
        solve(a, b, c, d);
    }
    return 0;
}

7-9 UVa1601 万圣节的早上，The Morning after Halloween ♥️ @

w*h（w,h <= 16）网格上有 n（n <= 3）个小写字母（代表鬼），要求把它们移到对应的大写字母里。每步可以同时移动多个鬼。但移动后不能两个鬼占用同一个位置，也不能再一步之内交换位置。

####                        ####        ####        ####        ####
 ab#                         ab#        a b#        acb#        ab #
#c##                        #c##        #c##        # ##        #c##
####                        ####        ####        ####        ####

状态数：(16^2)^3
每次转移：5^3，上下左右以及不动

// UVa1601 The Morning after Halloween
// This code implements the simpliest yet efficient-enough algorithm I'm aware of
// Readers are encouraged to experiment on other algorithms (especially for better efficiency!)
#include <cstdio>
#include <cstring>
#include <cctype>
#include <queue>
using namespace std;

const int maxs = 20;
const int maxn = 150;                                   // 75% cells plus 2 fake nodes
const int dx[] = { 1,-1,0,0,0 };                        // 4 moves, plus "no move"
const int dy[] = { 0,0,1,-1,0 };

inline int ID( int a, int b, int c ) {
    return (a<<16)|(b<<8)|c;
}

int s, t;                                         // starting/ending position of each ghost

int deg[maxn], G[maxn];                              // target cells for each move (including "no move")

inline bool conflict( int a, int b, int a2, int b2 ) {
    return a2 == b2 || (a2 == b && b2 == a);
}

int d[maxn][maxn][maxn];                                // distance from starting state
int bfs() {
    queue<int> q;
    memset( d, -1, sizeof(d) );
    q.push( ID( s, s, s ) );                   // starting node
    d[s][s][s] = 0;
    while( !q.empty(  ) ) {
        int u = q.front(); q.pop();
        int a = (u>>16)&0xff, b = (u>>8)&0xff, c = u&0xff;
        if( a == t && b == t && c == t ) {     // solution found
            return d[a][b][c];
        }
        for( int i = 0; i < deg[a]; i++ ) {
            int a2 = G[a][i];
            for( int j = 0; j < deg[b]; j++ ) {
                int b2 = G[b][j];
                if( conflict( a, b, a2, b2 ) ) { continue; }
                for( int k = 0; k < deg[c]; k++ ) {
                    int c2 = G[c][k];
                    if( conflict( a, c, a2, c2 ) ) { continue; }
                    if( conflict( b, c, b2, c2 ) ) { continue; }
                    if( d[a2][b2][c2] != -1      ) { continue; }
                    d[a2][b2][c2] = d[a][b][c]+1;
                    q.push( ID( a2, b2, c2 ) );
                }
            }
        }
    }
    return -1;
}

int main() {
    int w, h, n;

    while( scanf( "%d%d%d\n", &w, &h, &n ) == 3 && n ) {
        char maze;
        for( int i = 0; i < h; i++ ) {
            fgets(maze[i], 20, stdin);
        }

        // extract empty cells
        int cnt, x[maxn], y[maxn], id[maxs][maxs];      // cnt is the number of empty cells
        cnt = 0;
        for( int i = 0; i < h; i++ ) {
            for( int j = 0; j < w; j++ ) {
                if( maze[i][j] != '#' ) {
                    x[cnt] = i; y[cnt] = j; id[i][j] = cnt;
                    if( islower( maze[i][j] ) ) {
                        s[maze[i][j] - 'a'] = cnt;
                    } else if( isupper( maze[i][j] ) ) {
                        t[maze[i][j] - 'A'] = cnt;
                    }
                    cnt++;
                }
            }
        }

        // build a graph of empty cells
        for(int i = 0; i < cnt; i++) {
            deg[i] = 0;
            for( int dir = 0; dir < 5; dir++ ) {
                int nx = x[i]+dx[dir], ny = y[i]+dy[dir];
                // "Outermost cells of a map are walls" means we don't need to check out-of-bound
                if( maze[nx][ny] != '#' ) {
                    G[i][deg[i]++] = id[nx][ny];
                }
            }
        }

        // add fakes nodes so that in each case we have 3 ghosts. this makes the code shorter
        if( n <= 2 ) { deg[cnt] = 1; G[cnt] = cnt; s = t = cnt++; }
        if( n <= 1 ) { deg[cnt] = 1; G[cnt] = cnt; s = t = cnt++; }

        printf( "%d\n", bfs() );
    }
    return 0;
}

迭代加深搜索 @

埃及分数问题 ♥️ @

2/3 = 1/2 + 1/6，但是不能有 2/3 = 1/3 + 1/3。加数越少越好。其中最小分数越大越好。

解答树太夸张。深度不见底，宽度也没有边界。用 BFS 一层都搜不完。

用迭代加深搜索（iterative deepening）。

第 i 层，sum of before: c/d，第 i 个位 1/e，则还需要至少 (a/b-c/d)/(1/e) 个分数，总和才能达到 a/b。

例如：19/45 = 1/5 + 1/100 + …，至少需要 (19/45-1/5)/(1/101) = 23 项。

估计至少还要多少步才能出解。

// 埃及分数问题
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cassert>
using namespace std;

int a, b, maxd;

typedef long long LL;

LL gcd( LL a, LL b ) {
    return b == 0 ? a : gcd( b, a%b );
}

// 返回满足 1/c <= a/b 的最小 c
inline int get_first( LL a, LL b ) {
    return b/a+1;
}

const int maxn = 100 + 5;
LL v[maxn], ans[maxn];

// 如果当前解 v 比目前最优解 ans 更优，更新 ans
bool better( int d ) {
    for( int i = d; i >= 0; i-- ) {
        if( v[i] != ans[i] ) {
            return ans[i] == -1 || v[i] < ans[i];
        }
    }
    return false;
}

// 当前深度为 d，分母不能小于 from，分数之和恰好为 aa/bb
bool dfs( int d, int from, LL aa, LL bb ) {
    if( d == maxd ) {
        if( bb % aa ) { return false; }                         // aa/bb 必须是埃及分数
        v[d] = bb/aa;
        if( better( d ) ) {
            memcpy( ans, v, sizeof( LL ) * ( d+1 ) );           // 0..d
        }
        return true;
    }
    int ok = 0;
    from = max( from, get_first( aa, bb ) );                    // 枚举的起点
    for( int i = from; ; i++ ) {
        if( bb *(maxd+1-d) <= i*aa ) { break; }                 // 剪枝：如果剩下的 maxd+1-d 个分数全部都是 1/i，加起来仍然不超过 aa/bb，则无解
        v[d] = i;
        LL b2 = bb*i;                                           // 计算 aa/bb - 1/i，设结果为 a2/b2
        LL a2 = aa*i - bb;
        LL g = gcd( a2, b2 );                                   // 以便约分
        if( dfs( d+1, i+1, a2/g, b2/g ) ) { ok = true; }
    }
    return ok;
}

int main() {
    int kase = 0;
    while( cin >> a >> b ) {
        int ok = 0;
        for( maxd = 1; maxd <= 100; maxd++ ) {
            memset( ans, -1, sizeof(ans) );
            if( dfs( 0, get_first( a, b ), a, b ) ) { ok = 1; break; }
        }
        cout << "Case " << ++kase << ": ";
        if( ok ) {
            cout << a << "/" << b << "=";
            for( int i = 0; i < maxd; i++ ) {
                cout << "1/" << ans[i] << "+";
            }
            cout << "1/" << ans[maxd] << "\n";
        } else {
            cout << "No solution.\n";
        }
    }
    return 0;
}

$ echo 495 499 | ./a.out
Case 1: 495/499=1/2+1/5+1/6+1/8+1/3992+1/14970

7-10 UVa11212 编辑书稿，Editing a Book @

// UVa11212 Editing a Book
// Rujia Liu
// This implementation is not very fast, but easy to understand
#include<cstdio>
#include<cstring>
using namespace std;

const int maxn = 9;
int n, a[maxn];

bool is_sorted() {
    for(int i = 0; i < n-1; i++)
        if(a[i] >= a[i+1]) return false;
    return true;
}

// the number of integers with incorrect successor
int h() {
    int cnt = 0;
    for(int i = 0; i < n-1; i++)
        if(a[i]+1 != a[i+1]) cnt++;
    if(a[n-1] != n) cnt++;
    return cnt;
}

bool dfs(int d, int maxd) {
    if(d*3 + h() > maxd*3) return false;
    if(is_sorted()) return true;

    int b[maxn], olda[maxn];
    memcpy(olda, a, sizeof(a));
    for(int i = 0; i < n; i++)
        for(int j = i; j < n; j++) {
            // cut
            int cnt = 0;
            for(int k = 0; k < n; k++)
                if(k < i || k > j) b[cnt++] = a[k];

            // insert before position k
            for(int k = 0; k <= cnt; k++) {
                int cnt2 = 0;
                for(int p = 0; p < k; p++) a[cnt2++] = b[p];
                for(int p = i; p <= j; p++) a[cnt2++] = olda[p];
                for(int p = k; p < cnt; p++) a[cnt2++] = b[p];

                if(dfs(d+1, maxd)) return true;
                memcpy(a, olda, sizeof(a));
            }
        }
    return false;
}

int solve() {
    if(is_sorted()) return 0;
    int max_ans = 5; // after experiments, we found ans <= 5 for n <= 9
    for(int maxd = 1; maxd < max_ans; maxd++)
        if(dfs(0, maxd)) return maxd;
    return max_ans;
}

int main() {
    int kase = 0;
    while(scanf("%d", &n) == 1 && n) {
        for(int i = 0; i < n; i++) scanf("%d", &a[i]);
        printf("Case %d: %d\n", ++kase, solve());
    }
    return 0;
}

小结 @
- 直接枚举：效率不高。
- 枚举子集和排列：n 个元素的子集有 2ⁿ 个，可用递归的方法枚举（增量法和位向量法），也可以用二进制法枚举。递归法效率高，方便剪枝，缺点在于代码比较长。当 n <= 15 时，一般用二进制枚举。
  
  n 个不同元素的全排列有 n! 个。除了用递归的方法枚举，还可以用 STL 的 next_permutation，它可以处理重复元素的情况。
- 回溯法，回溯就是递归枚举，只不过可以提前终止递归，即回溯（backtracking）。
- 状态空间的搜索：本质上，状态空间搜索和图算法相似度比较大。
  
  最好掌握 Dijkstra、A* 以及 双向广度优先搜索。
- 迭代加深搜索，埃及分数和编辑书稿都是经典题。

竞赛题目选讲 @

7-11 UVa12325 Zombie’s Treasure Chest UVa12325.cpp @

// UVa12325 Zombie's Treasure Chest
#include<cstdio>
#include<algorithm>
using namespace std;

typedef long long LL;

int main(){
    int T;
    scanf("%d", &T);
    for(int kase = 1; kase <= T; kase++) {
        int n, s1, v1, s2, v2;
        scanf("%d%d%d%d%d", &n, &s1, &v1, &s2, &v2);
        if(s1 > s2){
            swap(s1, s2);
            swap(v1, v2);
        }
        LL ans = 0;
        if(n / s2 >= 65536){ // both s1 and s2 are small
            for(LL i = 0; i <= s1; i++){
                ans = max(ans, v2*i + (n-s2*i)/s1*v1);
            }
            for(LL i = 0; i <= s2; i++){
                ans = max(ans, v1*i + (n-s1*i)/s2*v2);
            }
        }else{ // s2 is large
            for(LL i = 0; s2*i <= n; i++)
                ans = max(ans, v2*i + (n-s2*i)/s1*v1);
        }
        printf("Case #%d: %lld\n", kase, ans);
    }
    return 0;
}

7-12 UVa1343 The Rotation Game UVa1343.cpp @

// UVa1343 The Rotation Game
// Rujia Liu
// This solutions uses IDA* instead of BFS described in the book, because it's shorter 8-)
// It's shorter because no need for lookup tables and "automatically" lexicographically smallest solution.
#include<cstdio>
#include<algorithm>
using namespace std;

/*
   00    01
   02    03
   04 05 06 07 08 09 10
   11    12
   13 14 15 16 17 18 19
   20    21
   22    23
   */

// lines E~H are computed with the help of rev[]
int line={
    { 0, 2, 6,11,15,20,22}, // A
    { 1, 3, 8,12,17,21,23}, // B
    {10, 9, 8, 7, 6, 5, 4}, // C
    {19,18,17,16,15,14,13}, // D
};

const int rev = {5, 4, 7, 6, 1, 0, 3, 2}; // reverse lines of each line

// center squares
const int center = {6, 7, 8, 11, 12, 15, 16, 17};

int a;
char ans;

bool is_final() {
    for(int i = 0; i < 8; i++)
        if (a[center[i]] != a[center]) return false;
    return true;
}

int diff(int target) {
    int ans = 0;
    for(int i = 0; i < 8; i++)
        if(a[center[i]] != target) ans++;
    return ans;
}

inline int h() {
    return min(min(diff(1), diff(2)), diff(3));
}

inline void move(int i) {
    int tmp = a[line[i]];
    for(int j = 0; j < 6; j++) a[line[i][j]] = a[line[i][j+1]];
    a[line[i]] = tmp;
}

bool dfs(int d, int maxd) {
    if(is_final()) {
        ans[d] = '\0';
        printf("%s\n", ans);
        return true;
    }
    if(d + h() > maxd) return false;
    for(int i = 0; i < 8; i++) {
        ans[d] = 'A' + i;
        move(i);
        if(dfs(d+1, maxd)) return true;
        move(rev[i]);
    }
    return false;
}

int main() {
    for(int i = 4; i < 8; i++)
        for(int j = 0; j < 7; j++) line[i][j] = line[rev[i]][6-j];

    while(scanf("%d", &a) == 1 && a) {
        for(int i = 1; i < 24; i++) scanf("%d", &a[i]);
        for(int i = 0; i < 24; i++) if(!a[i]) return 0;
        if(is_final()) {
            printf("No moves needed\n");
        } else {
            for(int maxd = 1; ; maxd++)
                if(dfs(0, maxd)) break;
        }
        printf("%d\n", a);
    }
    return 0;
}

7-13 UVa1374 Power Calculus UVa1374.cpp @

// UVa1374 Power Calculus
// Rujia Liu
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int maxans = 13; // we got it by experimenting

int n, a[maxans+1];

bool dfs(int d, int maxd) {
    if(a[d] == n) return true;
    if(d == maxd) return false;

    int maxv = a;
    for(int i = 1; i <= d; i++) maxv = max(maxv, a[i]);
    if((maxv << (maxd-d)) < n) return false;

    // Always use the last value.
    // I can't prove it, but we haven't found a counter-example for n <= 1000
    for(int i = d; i >= 0; i--) {
        a[d+1] = a[d] + a[i];
        if(dfs(d+1, maxd)) return true;
        a[d+1] = a[d] - a[i];
        if(dfs(d+1, maxd)) return true;
    }
    return false;
}

int solve(int n) {
    if(n == 1) return 0;
    a = 1;
    for(int maxd = 1; maxd < maxans; maxd++) {
        if(dfs(0, maxd)) return maxd;
    }
    return maxans;
}

int main() {
    while(scanf("%d", &n) == 1 && n) {
        printf("%d\n", solve(n));
    }
    return 0;
}

7-14 UVa1602 网格动物，Lattice Animals @

输入 n、w、h（1<=n<=10，1<=w,h<=n），求能放在 w*h 网格内里的不同的 n 连块的个数。

2x4 里面的 5 连块：

        --      --      --      --      --
    1|  ##      #        #      ##       #
    2|  ##      #       ##       #      ##
    3|   #      #       #       ##       #
    4|          ##      #                #

3x3 里面的 8 连块：

        ---     ---     ---
    1|  ###     ###     ###
    2|  ###     ###     # #
    3|   ##     # #     ###

如果用回溯法，和有很多重复枚举：

            ##
             #

             |
 +-------+---+--+------+
 |       |      |      |

 X                X
 ##     X##      ##    ##X
  #       #       #     #

Polyomino @

A polyomino [,pɒlɪ'ɒmɪnəʊ] is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling with a connected interior.

它们还有自己的名字：

Number of cells	Name
1	monomino
2	domino
3	tromino
4	tetromino
5	pentomino
6	hexomino
7	heptomino
8	octomino
9	nonomino
10	decomino
11	undecomino
12	dodecomino

The 18 one-sided pentominoes, including 6 mirrored pairs

The 35 free hexominoes, colored according to their symmetry.

refs and see also

Polyomino - Wikipedia, the free encyclopedia

// UVa1602 Lattice Animals
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <set>
using namespace std;

struct Cell {
    int x, y;
    Cell( int x=0, int y=0 ) : x(x), y(y) { }
    bool operator <( const Cell& rhs ) const {
        return x < rhs.x || (x == rhs.x && y < rhs.y);
    }
};

typedef set<Cell> Polyomino;

#define FOR_CELL(c, p) for( Polyomino::const_iterator c = (p).begin(); c != (p).end(); ++c )

inline Polyomino normalize( const Polyomino &p ) {
    int minX = p.begin()->x, minY = p.begin()->y;
    FOR_CELL( c, p ) {
        minX = min(minX, c->x);
        minY = min(minY, c->y);
    }
    Polyomino p2;
    FOR_CELL( c, p ) {
        p2.insert( Cell(c->x-minX, c->y-minY) );
    }
    return p2;
}

inline Polyomino rotate( const Polyomino &p ) {
    Polyomino p2;
    FOR_CELL( c, p ) {
        p2.insert( Cell(c->y, -c->x) );
    }
    return normalize(p2);
}

inline Polyomino flip( const Polyomino &p ) {
    Polyomino p2;
    FOR_CELL( c, p ) {
        p2.insert( Cell(c->x,-c->y) );
    }
    return normalize( p2 );
}

const int dx[] = {  -1,  1,  0,  0  };
const int dy[] = {   0,  0, -1,  1  };

const int maxn = 10;
set<Polyomino> poly[maxn+1];
int ans[maxn+1][maxn+1][maxn+1];

// add a cell to p0 and check whether it's new. If so, add to the polyonimo set
void check_polyomino( const Polyomino& p0, const Cell& c ) {
    Polyomino p = p0;
    p.insert(c);
    p = normalize(p);

    int n = p.size();
    for( int i = 0; i < 4; i++ ) {
        if( poly[n].count(p) ) { return; }
        p = rotate(p);
    }
    p = flip(p);
    for( int i = 0; i < 4; i++ ) {
        if( poly[n].count( p ) ) { return; }
        p = rotate(p);
    }
    poly[n].insert(p);
}

void generate() {
    Polyomino s;
    s.insert( Cell(0, 0) );
    poly.insert(s);

    // generate
    for( int n = 2; n <= maxn; n++ ) {
        for( set<Polyomino>::iterator p = poly[n-1].begin(); p != poly[n-1].end(); ++p ) {
            FOR_CELL( c, *p ) {
                for( int dir = 0; dir < 4; dir++ ) {
                    Cell newc(c->x + dx[dir], c->y + dy[dir]);
                    if( p->count(newc) == 0 ) { check_polyomino(*p, newc); }
                }
            }
        }
    }

    // precompute answers
    for( int n = 1; n <= maxn; n++ ) {
        for( int w = 1; w <= maxn; w++ ) {
            for( int h = 1; h <= maxn; h++ ) {
                int cnt = 0;
                for( set<Polyomino>::iterator p = poly[n].begin(); p != poly[n].end(); ++p ) {
                    int maxX = 0, maxY = 0;
                    FOR_CELL(c, *p) {
                        maxX = max( maxX, c->x );
                        maxY = max( maxY, c->y );
                    }
                    if( min( maxX, maxY ) < min( h, w ) && max( maxX, maxY ) < max( h, w ) ) {
                        ++cnt;
                    }
                }
                ans[n][w][h] = cnt;
            }
        }
    }
}

int main() {
    generate();

    int n, w, h;
    while( scanf( "%d%d%d", &n, &w, &h ) == 3 ) {
        printf( "%d\n", ans[n][w][h] );
    }
    return 0;
}

7-15 UVa1603 Square Destroyer UVa1603.cpp @

用迭代加深。或者 DLX 算法。

// UVa1603 Square Destroyer
// Rujia Liu
// This code implements a variant of an algorithm presented in a book. It's simple yet efficient.
// Readers are encouraged to experiment on other algorithms.
// However, it's still slow for n=5 and m=0 (which is NOT in judge input)
// If you really want an efficient solution, learn DLX (Algorithm X with dancing links)
// DLX is well expained (with code) in my other book <<Beginning Algorithm Contests -- Training Guide>>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
using namespace std;

const int maxs = 60; // number of squares: 25+16+9+4+1=55
const int maxm = 60; // number of matches: 2*5*(5+1)=60

int n, exists[maxm]; // matches
int s, size[maxs], fullsize[maxs], contains[maxs][maxm]; // squares
int best;

inline int row_match(int x, int y) {
    return (2*n+1)*x+y;
}

inline int col_match(int x, int y) {
    return (2*n+1)*x+n+y;
}

// number of matches in a full n*n grid
inline int match_count(int n) {
    return 2*n*(n+1);
}

void init() {
    int m, v;
    scanf("%d%d", &n, &m);
    for(int i = 0; i < match_count(n); ++i) exists[i] = 1;
    while(m--) {
        scanf("%d", &v);
        exists[v-1] = 0;
    }

    // collect full squares
    s = 0;
    memset(contains, 0, sizeof(contains));
    for(int i = 1; i <= n; i++) // side length
        for(int x = 0; x <= n-i; x++)
            for(int y = 0; y <= n-i; y++) {
                size[s] = 0;
                fullsize[s] = 4*i; // number of matches in a complete square
                for(int j = 0; j < i; j++) {
                    int a = row_match(x, y+j); // up
                    int b = row_match(x+i, y+j); // down
                    int c = col_match(x+j, y); // left
                    int d = col_match(x+j, y+i); // right
                    contains[s][a] = 1;
                    contains[s][b] = 1;
                    contains[s][c] = 1;
                    contains[s][d] = 1;
                    size[s] += exists[a] + exists[b] + exists[c] + exists[d]; // number of matches now
                }
                ++s;
            }
}

int find_square() {
    for(int i = 0; i < s; i++)
        if(size[i] == fullsize[i]) return i;
    return -1;
}

void dfs(int dep) {
    if(dep >= best) return;

    int k = find_square();
    if(k == -1) {
        best = dep;
        return;
    }

    // remove a match in that square
    for(int i = 0; i < match_count(n); i++)
        if(contains[k][i]) {
            for(int j = 0; j < s; j++)
                if(contains[j][i]) size[j]--;
            dfs(dep + 1);
            for(int j = 0; j < s; j++)
                if(contains[j][i]) size[j]++;
        }
}

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        init();
        best = n*n;
        dfs(0);
        printf("%d\n", best);
    }
    return 0;
}

✂️ 2016/00/00 上午 9:30:00 0. 高效算法设计 @

算法分析初步 @
- 渐进时间复杂度
- 上界分析
- 分治法
- 正确对待算法分析结果
再谈排序与检索 @
- 归并排序
- 快速排序
递归与分治

贪心法 @

背包相关问题
区间相关问题

Huffman 编码 ♥️ @

给定一个英文字符串，使用 0 和 1 对其进行编码，求最优前缀编码，使其所需要的比特数最少。

哈弗曼编码。

// 本题考查哈弗曼编码，但只需要统计哈弗曼编码后的总码长即可，
// 没必要建哈弗曼树得出哈弗曼编码
#include <cstdio>
#include <queue>
#include <string>
#include <iostream>
#include <functional>

using namespace std;

int main() {
    vector<int> count( 128, 0 );    // count[i] 记录 ASCII 码为 i 的字符的出现次数

    int sum;
    priority_queue<int, vector<int>, greater<int> > pq;     // 小根堆，队列头为最小元素

    string line;
    while ( getline(cin, line) ) {
        if( line == "END" ) { break; }
        sum = 0;                        // 清零
        const int len = line.size();
        for( int i = 0; i < len; ++i ) {
            count[line[i]]++;
        }
        for( int i = 0; i < 128; ++i ) {
            if (count[i] > 0) {
                pq.push(count[i]);
                count[i] = 0;
            }
        }
        while( pq.size() > 1 ) {
            const int a = pq.top(); pq.pop();
            const int b = pq.top(); pq.pop();
            sum += a + b;
            pq.push(a + b);
        }
        if ( sum == 0 ) {               // 此时pq中只有一个元素
            sum = len;
        }

        // these is no such thing as `pq.clear()';
        while( !pq.empty() ) { pq.pop(); }

        // 注意精度设置
        printf( "%d, %d, %.1f\n", 8 * len, sum, ((double)8 * len) / sum );
    }
    return 0;
}

算法设计与优化策略 @

8-1 UVa120 Stacks of Flapjacks UVa120.cpp @

// UVa120 Stacks of Flapjacks
// Rujia Liu
#include<cstdio>
#include<iostream>
#include<sstream>
#include<algorithm>
using namespace std;

const int maxn = 30 + 5;
int n, a[maxn];

// 翻转a[0..p]
void flip(int p) {
    for(int i = 0; i < p-i; i++)
        swap(a[i], a[p-i]);
    printf("%d ", n-p);
}

int main() {
    string s;
    while(getline(cin, s)) {
        cout << s << "\n";
        stringstream ss(s);
        n = 0;
        while(ss >> a[n]) n++;
        for(int i = n-1; i > 0; i--) {
            int p = max_element(a, a+i+1) - a; // 元素a[0..i]中的最大元素
            if(p == i) continue;
            if(p > 0) flip(p); // flip(0)没啥意思，是不？
            flip(i);
        }
        printf("0\n");
    }
    return 0;
}

8-2 UVa1605 Building for UN UVa1605.cpp @

// UVa1605 Building for UN
// Rujia Liu
#include<cstdio>
using namespace std;

char country(int i) {
    if(i < 26) return 'A' + i;
    return 'a' + i - 26;
}

int main() {
    int n;
    while(scanf("%d", &n) == 1) {
        printf("2 %d %d\n", n, n);
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < n; j++) printf("%c", country(i));
            printf("\n");
        }
        printf("\n");
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < n; j++) printf("%c", country(j));
            printf("\n");
        }
    }
    return 0;
}

8-3 UVa1152 4 Values Whose Sum is Zero UVa1152.cpp @

// UVa1152 4 Values Whose Sum is Zero
// Rujia Liu
#include<cstdio>
#include<algorithm>
using namespace std;

const int maxn = 4000 + 5;
int n, c, A[maxn], B[maxn], C[maxn], D[maxn], sums[maxn*maxn];

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        scanf("%d", &n);
        for(int i = 0; i < n; i++)
            scanf("%d%d%d%d", &A[i], &B[i], &C[i], &D[i]);
        c = 0;
        for(int i = 0; i < n; i++)
            for(int j = 0; j < n; j++)
                sums[c++] = A[i] + B[j];
        sort(sums, sums+c);
        long long cnt = 0;
        for(int i = 0; i < n; i++)
            for(int j = 0; j < n; j++)
                cnt += upper_bound(sums, sums+c, -C[i]-D[j]) - lower_bound(sums, sums+c, -C[i]-D[j]);
        printf("%lld\n", cnt);
        if(T) printf("\n");
    }
    return 0;
}

8-4 UVa11134 Fabled Rooks UVa11134.cpp @

// UVa11134 Fabled Rooks
// Rujia Liu
#include<cstdio>
#include<cstring>
#include <algorithm>
using namespace std;

// solve 1-D problem: find c so that a[i] <= c[i] <= b[i] (0 <= i < n)
bool solve(int *a, int *b, int *c, int n) {
    fill(c, c+n, -1);
    for(int col = 1; col <= n; col++) {
        // find a rook with smalleset b that is not yet assigned
        int rook = -1, minb = n+1;
        for(int i = 0; i < n; i++)
            if(c[i] < 0 && b[i] < minb && col >= a[i]) { rook = i; minb = b[i]; }
        if(rook < 0 || col > minb) return false;
        c[rook] = col;
    }
    return true;
}

const int maxn = 5000 + 5;
int n, x1[maxn], y1[maxn], x2[maxn], y2[maxn], x[maxn], y[maxn];

int main() {
    while(scanf("%d", &n) == 1 && n) {
        for (int i = 0; i < n; i++)
            scanf("%d%d%d%d", &x1[i], &y1[i], &x2[i], &y2[i]);
        if(solve(x1, x2, x, n) && solve(y1, y2, y, n))
            for (int i = 0; i < n; i++) printf("%d %d\n", x[i], y[i]);
        else
            printf("IMPOSSIBLE\n");
    }
    return 0;
}

8-5 UVa11054 Wine trading in Gergovia UVa11054.cpp @

// UVa11054 Wine trading in Gergovia
// Rujia Liu
#include<iostream>
#include<algorithm>
using namespace std;

int main() {
    int n;
    while(cin >> n && n) {
        long long ans = 0, a, last = 0;
        for(int i = 0; i < n; i++) {
            cin >> a;
            ans += abs(last);
            last += a;
        }
        cout << ans << "\n";
    }
    return 0;
}

8-6 UVa1606 Amphiphilic Carbon Molecules UVa1606.cpp @

// UVa1606 Amphiphilic Carbon Molecules
// Rujia Liu
// To make life a bit easier, we change each color 1 point into color 0.
// Then we only need to find an angle interval with most points. See code for details.
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;

const int maxn = 1000 + 5;

struct Point {
    int x, y;
    double rad; // with respect to current point
    bool operator<(const Point &rhs) const {
        return rad < rhs.rad;
    }
}op[maxn], p[maxn];

int n, color[maxn];

// from O-A to O-B, is it a left turn?
bool Left(Point A, Point B) {
    return A.x * B.y - A.y * B.x >= 0;
}

int solve() {
    if(n <= 2) return 2;
    int ans = 0;

    // pivot point
    for(int i = 0; i < n; i++) {
        int k = 0;

        // the list of other point, sorted in increasing order of rad
        for(int j = 0; j < n; j++)
            if(j != i) {
                p[k].x = op[j].x - op[i].x;
                p[k].y = op[j].y - op[i].y;
                if(color[j]) { p[k].x = -p[k].x; p[k].y = -p[k].y; }
                p[k].rad = atan2(p[k].y, p[k].x);
                k++;
            }
        sort(p, p+k);

        // sweeping. cnt is the number of points whose rad is between p[L] and p[R]
        int L = 0, R = 0, cnt = 2;
        while(L < k) {
            if(R == L) { R = (R+1)%k; cnt++; } // empty interval
            while(R != L && Left(p[L], p[R])) { R = (R+1)%k; cnt++; } // stop when [L,R] spans across > 180 degrees
            cnt--;
            L++;
            ans = max(ans, cnt);
        }
    }
    return ans;
}

int main() {
    while(scanf("%d", &n) == 1 && n) {
        for(int i = 0; i < n; i++)
            scanf("%d%d%d", &op[i].x, &op[i].y, &color[i]);
        printf("%d\n", solve());
    }
    return 0;
}

8-7 UVa11572 Unique snowflakes UVa11572.cpp @

// UVa11572 Unique snowflakes
// Rujia Liu
#include<cstdio>
#include<set>
#include<algorithm>
using namespace std;

const int maxn = 1000000 + 5;
int A[maxn];

int main() {
    int T, n;
    scanf("%d", &T);
    while(T--) {
        scanf("%d", &n);
        for(int i = 0; i < n; i++) scanf("%d", &A[i]);

        set<int> s;
        int L = 0, R = 0, ans = 0;
        while(R < n) {
            while(R < n && !s.count(A[R])) s.insert(A[R++]);
            ans = max(ans, R - L);
            s.erase(A[L++]);
        }
        printf("%d\n", ans);
    }
    return 0;
}

// UVa11572 Unique snowflakes
// Rujia Liu
// 算法二：记录位置i的上个相同元素位置last[i]
#include<cstdio>
#include<map>
using namespace std;

const int maxn = 1000000 + 5;
int A[maxn], last[maxn];
map<int, int> cur;

int main() {
    int T, n;
    scanf("%d", &T);
    while(T--) {
        scanf("%d", &n);
        cur.clear();
        for(int i = 0; i < n; i++) {
            scanf("%d", &A[i]);
            if(!cur.count(A[i])) last[i] = -1;
            else last[i] = cur[A[i]];
            cur[A[i]] = i;
        }

        int L = 0, R = 0, ans = 0;
        while(R < n) {
            while(R < n && last[R] < L) R++;
            ans = max(ans, R - L);
            L++;
        }
        printf("%d\n", ans);
    }
    return 0;
}

// UVa11572 Unique snowflakes
// Rujia Liu
// 算法二：记录位置i的上个相同元素位置last[i]。使用hash_map（gcc扩展）
#include<cstdio>
#include<ext/hash_map>
using namespace std;
using namespace __gnu_cxx; // hash_map

const int maxn = 1000000 + 5;
int A[maxn], last[maxn];
hash_map<int, int> cur;

int main() {
    int T, n;
    scanf("%d", &T);
    while(T--) {
        scanf("%d", &n);
        cur.clear();
        for(int i = 0; i < n; i++) {
            scanf("%d", &A[i]);
            if(!cur.count(A[i])) last[i] = -1;
            else last[i] = cur[A[i]];
            cur[A[i]] = i;
        }

        int L = 0, R = 0, ans = 0;
        while(R < n) {
            while(R < n && last[R] < L) R++;
            ans = max(ans, R - L);
            L++;
        }
        printf("%d\n", ans);
    }
    return 0;
}

8-8 UVa1471 Defense Lines UVa1471.cpp @

// UVa1471 Defense Lines
// Rujia Liu
// Algorithm 1: use STL set to maintain the candidates.
// This is a little bit more intuitive, but less efficient (than algorithm 2)
#include<cstdio>
#include<set>
#include<cassert>
using namespace std;

const int maxn = 200000 + 5;
int n, a[maxn], f[maxn], g[maxn];

struct Candidate {
    int a, g;
    Candidate(int a, int g):a(a),g(g) {}
    bool operator < (const Candidate& rhs) const {
        return a < rhs.a;
    }
};

set<Candidate> s;

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        scanf("%d", &n);
        for(int i = 0; i < n; i++)
            scanf("%d", &a[i]);
        if(n == 1) { printf("1\n"); continue; }

        // g[i] is the length of longest increasing continuous subsequence ending at i
        g = 1;
        for(int i = 1; i < n; i++)
            if(a[i-1] < a[i]) g[i] = g[i-1] + 1;
            else g[i] = 1;

        // f[i] is the length of longest increasing continuous subsequence starting from i
        f[n-1] = 1;
        for(int i = n-2; i >= 0; i--)
            if(a[i] < a[i+1]) f[i] = f[i+1] + 1;
            else f[i] = 1;

        s.clear();
        s.insert(Candidate(a, g));
        int ans = 1;
        for(int i = 1; i < n; i++) {
            Candidate c(a[i], g[i]);
            set<Candidate>::iterator it = s.lower_bound(c); // first one that is >= c
            bool keep = true;
            if(it != s.begin()) {
                Candidate last = *(--it); // (--it) points to the largest one that is < c
                int len = f[i] + last.g;
                ans = max(ans, len);
                if(c.g <= last.g) keep = false;
            }

            if(keep) {
                s.erase(c); // if c.a is already present, the old g must be <= c.g
                s.insert(c);
                it = s.find(c); // this is a bit cumbersome and slow but it's clear
                it++;
                while(it != s.end() && it->a > c.a && it->g <= c.g) s.erase(it++);
            }
        }
        printf("%d\n", ans);
    }
    return 0;
}

8-9 UVa1451 Average UVa1451.cpp @

// UVa1451 Average
// Rujia Liu
#include<cstdio>
using namespace std;

const int maxn = 100000 + 5;

int n, L;
char s[maxn];
int sum[maxn], p[maxn]; // average of i~j is (sum[j]-sum[i-1])/(j-i+1)

// compare average of x1~x2 and x3~x4
int compare_average(int x1, int x2, int x3, int x4) {
    return (sum[x2]-sum[x1-1]) * (x4-x3+1) - (sum[x4]-sum[x3-1]) * (x2-x1+1);
}

int main() {
    int T;
    scanf("%d", &T);

    while(T--) {
        scanf("%d%d%s", &n, &L, s+1);

        sum = 0;
        for(int i = 1; i <= n; i++) sum[i] = sum[i-1] + s[i] - '0';

        int ansL = 1, ansR = L;

        // p[i..j) is the sequence of candidate start points
        int i = 0, j = 0;
        for (int t = L; t <= n; t++) { // end point
            while (j-i > 1 && compare_average(p[j-2], t-L, p[j-1], t-L) >= 0) j--; // remove concave points
            p[j++] = t-L+1; // new candidate

            while (j-i > 1 && compare_average(p[i], t, p[i+1], t) <= 0) i++; // update tangent point

            // compare and update solution
            int c = compare_average(p[i], t, ansL, ansR);
            if (c > 0 || c == 0 && t - p[i] < ansR - ansL) {
                ansL = p[i]; ansR = t;
            }
        }
        printf("%d %d\n", ansL, ansR);
    }
    return 0;
}

8-10 UVa714 Copying Books UVa714.cpp @

// UVa714 Copying Books
// Rujia Liu
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxm = 500 + 5;
int m, k, p[maxm];

// how many scribers needed if each scriber can work on at most maxp pages
int solve(long long maxp) {
    long long done = 0;
    int ans = 1;
    for(int i = 0; i < m; i++) {
        if(done + p[i] <= maxp) done += p[i];
        else { ans++; done = p[i]; }
    }
    return ans;
}

int last[maxm]; // last[i] = 1 iff i is the last book assigned to someone
void print(long long ans) {
    long long done = 0;
    memset(last, 0, sizeof(last));
    int remain = k;
    for(int i = m-1; i >= 0; i--) {
        if(done + p[i] > ans || i+1 < remain) {
            last[i] = 1; remain--; done = p[i];
        }
        else {
            done += p[i];
        }
    }
    for(int i = 0; i < m-1; i++) {
        printf("%d ", p[i]);
        if(last[i]) printf("/ ");
    }
    printf("%d\n", p[m-1]);
}

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        scanf("%d%d", &m, &k);
        long long tot = 0;
        int maxp = -1;
        for(int i = 0; i < m; i++) {
            scanf("%d", &p[i]);
            tot += p[i];
            maxp = max(maxp, p[i]);
        }
        long long L = maxp, R = tot;
        while(L < R) {
            long long M = L + (R-L)/2;
            if(solve(M) <= k) R = M; else L = M+1;
        }
        print(L);
    }
    return 0;
}

8-11 UVa10954 Add All UVa10954.cpp @

// UVa10954 Add All
// Rujia Liu
#include<cstdio>
#include<queue>
using namespace std;

int main() {
    int n, x;
    while(scanf("%d", &n) == 1 && n) {
        priority_queue<int, vector<int>, greater<int> > q;
        for(int i = 0; i < n; i++) { scanf("%d", &x); q.push(x); }
        int ans = 0;
        for(int i = 0; i < n-1; i++) {
            int a = q.top(); q.pop();
            int b = q.top(); q.pop();
            ans += a+b;
            q.push(a+b);
        }
        printf("%d\n", ans);
    }
    return 0;
}

8-12 UVa12627 Erratic Expansion UVa12627.cpp @

// UVa12627 Erratic Expansion
// Rujia Liu
#include<iostream>
using namespace std;

// how many red balloons after k hours
long long c(int i) {
    return i == 0 ? 1 : c(i-1)*3;
}

// how many red balloons in the first i rows, after k hours
long long f(int k, int i) {
    if(i == 0) return 0;
    if(k == 0) return 1;

    int k2 = 1 << (k-1);
    if(i >= k2) return f(k-1, i-k2) + c(k-1)*2;
    else return f(k-1, i) * 2;
}

// how many red balloons in the last i rows, after k hours
long long g(int k, int i) {
    if(i == 0) return 0;
    if(k == 0) return 1;

    int k2 = 1 << (k-1);
    if(i >= k2) return g(k-1, i-k2) + c(k-1);
    else return g(k-1,i);
}

int main() {
    int T, k, a, b;
    cin >> T;
    for(int kase = 1; kase <= T; kase++) {
        cin >> k >> a >> b;
        cout << "Case " << kase << ": " << f(k, b) - f(k, a-1) << "\n";
    }
    return 0;
}

8-13 UVa11093 Just Finish it up UVa11093.cpp @

// UVa11093 Just Finish it up
// Rujia Liu
#include<cstdio>

const int maxn = 100000 + 5;
int n, p[maxn], q[maxn];

// returns s if success
// otherwise, return the station you failed to reach
// if you failed to reach the start, return -1
int go(int s) {
    int fuel = p[s] - q[s];
    for(int i = (s+1)%n; i != s; i = (i+1)%n) {
        if(fuel < 0) return i;
        fuel += p[i] - q[i];
    }
    if(fuel < 0) return -1; // this means sum(p) < sum(q), so this case is impossible
    return s; // success
}

int solve() {
    int start = 0;
    for(;;) {
        int finish = go(start);
        if(finish < start) return -1; // wrapped around, or go(start) returns -1
        if(finish == start) return start;
        start = finish;
    }
}

int main() {
    int T;
    scanf("%d", &T);
    for(int kase = 1; kase <= T; kase++) {
        scanf("%d", &n);
        for(int i = 0; i < n; i++) scanf("%d", &p[i]);
        for(int i = 0; i < n; i++) scanf("%d", &q[i]);
        int ans = solve();
        printf("Case %d: ", kase);
        if(ans < 0) printf("Not possible\n");
        else printf("Possible from station %d\n", ans+1);
    }
    return 0;
}

8-14 UVa1607 Gates UVa1607.cpp @

// UVa1607 Gates
// Rujia Liu
#include<cstdio>
#include<algorithm>
using namespace std;

const int maxm = 200000 + 5;

int n, m;

struct Gates {
    int a, b, o;
} gates[maxm];

// returns the output of input 000..0111...1 (there are k 0's)
int output(int k) {
    for(int i = 1; i <= m; i++) {
        int a = gates[i].a;
        int b = gates[i].b;
        int va = a < 0 ? -a > k : gates[a].o;
        int vb = b < 0 ? -b > k : gates[b].o;
        gates[i].o = !(va && vb);
    }
    return gates[m].o;
}

// returns k such that
// 1. output(k) = output(n)
// 2. output(k-1) = output(0)
int solve(int vn) {
    int L = 1, R = n;
    while(L < R) {
        int M = L + (R-L)/2;
        if(output(M) == vn) R = M; else L = M+1;
    }
    return L;
}

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        scanf("%d%d", &n, &m);
        for (int i = 1; i <= m; i++)
            scanf("%d%d", &gates[i].a, &gates[i].b);
        int v0 = output(0);
        int vn = output(n);
        if(v0 == vn) {
            for(int i = 1; i <= n; i++) printf("0");
        } else {
            int x = solve(vn);
            for(int i = 1; i < x; i++) printf("0");
            printf("x");
            for(int i = x+1; i <= n; i++) printf("1");
        }
        printf("\n");
    }
    return 0;
}

8-15 UVa12174 Shuffle UVa12174.cpp @

// UVa12174 Shuffle
// Rujia Liu
#include<iostream>
#include<vector>
using namespace std;

const int maxn = 100000 + 5;
int s, n, x[maxn*3], cnt[maxn], ok[maxn*2];

int main() {
    int T;
    cin >> T;
    while(T--) {
        cin >> s >> n;

        // add s "-1" to the left/right of orriginal sequence
        // so we don't have to worry about negative subscript or wrapping round
        fill(x, x+n+2*s, -1);
        for(int i = 0; i < n; i++) cin >> x[i+s];

        int tot = 0; // how many different integers in current sliding window
        fill(cnt+1, cnt+s+1, 0); // cnt[i] is the number of occurrence of i in the current sliding window
        fill(ok, ok+n+s+1, 0);   // ok[i] = 1 iff the i-th sliding window didn't have duplicate numbers

        // compute "ok" array
        for(int i = 0; i < n+s+1; i++) {
            if (tot == s) ok[i] = 1;              // complete window
            if (i < s && tot == i) ok[i] = 1;     // incomplete windows on the left side
            if (i > n && tot == n+s-i) ok[i] = 1; // incomplete windows on the right side

            // update cnt and tot for the next sliding window
            if (i == n+s) break; // no more sliding windows, so we stop here
            if (x[i] != -1 && --cnt[x[i]]==0) tot--; // remove the first one
            if (x[i+s] != -1 && cnt[x[i+s]]++==0) tot++; // add the next one
        }

        // check each possible answer
        int ans = 0;
        for(int i = 0; i < s; i++) {
            int valid = 1;
            for (int j = i; j < n+s+1; j += s)
                if(!ok[j]) valid = 0;;
            if(valid) ans++;
        }
        if(ans == n+1) ans = s; // special case
        cout << ans << "\n";
    }
    return 0;
}

8-16 UVa1608 Non-boring sequences UVa1608.cpp @

// UVa1608 Non-boring sequences
// Rujia Liu
#include<cstdio>
#include<map>
using namespace std;

const int maxn = 200000 + 5;
int A[maxn], prev[maxn], next[maxn];
map<int, int> cur;

inline bool unique(int p, int L, int R) {
    return prev[p] < L && next[p] > R;
}

bool check(int L, int R) {
    if(L >= R) return true;
    for(int d = 0; L+d <= R-d; d++) {
        if(unique(L+d, L, R))
            return check(L, L+d-1) && check(L+d+1, R);
        if(L+d == R-d) break;
        if(unique(R-d, L, R))
            return check(R-d+1, R) && check(L, R-d-1);
    }
    return false;
}

int main() {
    int T, n;
    scanf("%d", &T);
    while(T--) {
        scanf("%d", &n);
        cur.clear();
        for(int i = 0; i < n; i++) {
            scanf("%d", &A[i]);
            if(!cur.count(A[i])) prev[i] = -1;
            else prev[i] = cur[A[i]];
            cur[A[i]] = i;
        }
        cur.clear();
        for(int i = n-1; i >= 0; i--) {
            if(!cur.count(A[i])) next[i] = n;
            else next[i] = cur[A[i]];
            cur[A[i]] = i;
        }

        if(check(0, n-1)) printf("non-boring\n");
        else printf("boring\n");
    }
    return 0;
}

8-17 UVa1609 Foul Play UVa1609.cpp @

// UVa1609  Foul Play
// Rujia Liu

#include<cstdio>
#include<vector>
using namespace std;

const int maxn = 1024 + 5;
char table[maxn][maxn];

int main() {
    int n;
    while(scanf("%d", &n) == 1) {
        for(int i = 1; i <= n; i++) scanf("%s", table[i]+1);

        vector<int> win, lose; // teams that team 1 win/lose against.
        for(int i = 2; i <= n; i++)
            if(table[i] == '1') win.push_back(i);
            else lose.push_back(i);

        int nt = n;
        while(nt > 1) {
            vector<int> win2, lose2, final; // phase 3/4

            // Phase 1
            for(int i = 0; i < lose.size(); i++) {
                int tlose = lose[i];
                bool matched = false;
                for(int j = 0; j < win.size(); j++) {
                    int& twin = win[j];
                    if(twin > 0 && table[twin][tlose] == '1') {
                        printf("%d %d\n", twin, tlose);
                        win2.push_back(twin); // go to the next round
                        twin = 0; // not available
                        matched = true;
                        break;
                    }
                }
                if(!matched) final.push_back(tlose); // to phase 3/4
            }

            // Phase 2
            bool first = true;
            for(int i = 0; i < win.size(); i++) {
                int twin = win[i];
                if(twin > 0) {
                    if(first) { printf("1 %d\n", twin); first = false; }
                    else final.push_back(twin);
                }
            }

            // Phase 3/4
            for(int i = 0; i < final.size(); i += 2) {
                printf("%d %d\n", final[i], final[i+1]);
                int keep = final[i];
                if(table[final[i+1]][keep] == '1') keep = final[i+1];
                if(table[keep] == '1') win2.push_back(keep);
                else lose2.push_back(keep);
            }
            win = win2;
            lose = lose2;
            nt >>= 1;
        }
    }
    return 0;
}

8-18 UVa1442 Cave uva1442.cpp @

// UVa1442 Cav
// Rujia Liu
#include<cstdio>
#include<algorithm>
using namespace std;

const int maxn = 1000000 + 5;
int n, p[maxn], s[maxn], h[maxn];
int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        scanf("%d", &n);
        for(int i = 0; i < n; i++) scanf("%d", &p[i]);
        for(int i = 0; i < n; i++) scanf("%d", &s[i]);

        int ans = 0, level = s;
        for(int i = 0; i < n; i++) {
            if(p[i] > level) level = p[i];
            if(s[i] < level) level = s[i];
            h[i] = level;
        }
        level = s[n-1];
        for(int i = n-1; i >= 0; i--) {
            if(p[i] > level) level = p[i];
            if(s[i] < level) level = s[i];
            ans += min(h[i], level) - p[i];
        }
        printf("%d\n", ans);
    }
    return 0;
}

8-19 UVa12265 Selling Land UVa12265.cpp @

// UVa12265 Selling Land
// Rujia Liu
// This code implements the algorithm described in the book
// Another way is: still use a stack to maintain the "staircase" shape
// But don't eliminate non-optimal rectangles in the stairecase.
// instead, let maxp[c] be the maximal half-perimeter whose rightmost column is c, which can be calculated with dp.
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int maxn = 1000 + 10;

char s[maxn][maxn];
int height[maxn], ans[maxn*2];

struct Rect {
    int c, h;
    Rect(int c=0, int h=0):c(c),h(h){}
};

Rect rect[maxn]; // stack

int main() {
    int n, m, T;
    scanf("%d", &T);
    while(T--) {
        scanf("%d%d", &n, &m);
        for(int i = 0; i < n; i ++) scanf("%s", s[i]);

        memset(height, 0, sizeof(height));
        memset(ans, 0, sizeof(ans));
        for(int i = 0; i < n; i ++) {
            int top = -1;
            for(int j = 0; j < m; j ++) {
                if(s[i][j] == '#') {
                    height[j] = 0;
                    top = -1; // clear stack
                } else {
                    height[j]++;
                    Rect r(j, height[j]);
                    if(top < 0) rect[++top] = r;
                    else {
                        while(top >= 0 && r.h <= rect[top].h) r.c = rect[top--].c;
                        if(top < 0 || r.h - r.c > rect[top].h - rect[top].c) rect[++top] = r;
                    }
                    ans[j-rect[top].c+rect[top].h+1]++;
                }
            }
        }
        for(int i = 1; i <= n + m; i++)
            if(ans[i]) printf("%d x %d\n", ans[i], i*2);
    }
    return 0;
}

✂️ 2016/00/00 上午 9:30:00 0. more BFS, DFS @

chap9. BFS @

maze ♥️ @

input:

    0 1 0 0 0
    0 1 0 1 0
    0 0 0 0 0
    0 1 1 1 0
    0 0 0 1 0

output:

    (0, 0)
    (1, 0)
    (2, 0)
    (2, 1)
    (2, 2)
    (2, 3)
    (2, 4)
    (3, 4)
    (4, 4)

POJ 3984 迷宫问题, http://poj.org/problem?id=3984

C version @

#include <stdio.h>
#include <cstring>
#include <queue>
using namespace std;

const char name[] = { 'U', 'R', 'D', 'L' };    //      |
const int dx[] = { -1, 0, 1, 0 };              //      |
const int dy[] = { 0, 1, 0, -1 };              //      V  rowsise: x

typedef struct state_t {
    int data;
    int action;
    int father;
} state_t;

const int MAXN = 5;
int m = MAXN, n = MAXN;                                 // 迷宫的行数，列数
int map[MAXN][MAXN];                                    // 迷宫，0 表示空地，1 表示障碍物

const int STATE_MAX = MAXN * MAXN;                      // 状态总数
state_t nodes[STATE_MAX];
int state_hash(  const state_t &s ) {
    return s.data;
}
int state_index( const state_t &s ) {
    return state_hash(s);
}

void print_action(const int end) {
    if( nodes[end].father == -1 ) { return; }           // no father
    print_action( nodes[end].father );
    putchar( name[nodes[end].action] );
}
void print_path( const int end ) {
    if( nodes[end].father != -1 ) {                     // starting point
        print_path( nodes[end].father );
    }
    printf("(%d, %d)\n", end / n, end % n);
}

const state_t END = { 24, -1, -1 };                     // (4, 4)
bool state_is_target( const state_t &s ) {              // end point
    return s.data == END.data;
}

const int HASH_CAPACITY = STATE_MAX;
bool visited[HASH_CAPACITY];
void hashset_init() {
    memset( visited, 0, sizeof(visited) );
}
bool hashset_find( const state_t &s ) {
    return visited[state_hash(s)] == true;
}
void hashset_insert( const state_t &s ) {
    visited[state_hash(s)] = true;
}

int x, y;                                               // 扩展点，即当前位置
int action_cur;
const int ACTION_BEGIN = 0;
const int ACTION_END   = 4;
void state_extend_init(const state_t &s) {
    action_cur = ACTION_BEGIN;
    x = s.data / n;
    y = s.data % n;
}

bool state_extend( const state_t &s, state_t &next ) {
    while( action_cur < ACTION_END ) {
        const int nx = x + dx[action_cur];
        const int ny = y + dy[action_cur];
        if( 0 <= nx && nx < m && 0 <= ny && ny < n && !map[nx][ny] ) {  // in scope, and empty
            next.data = nx * n + ny;
            if( !hashset_find(next) ) {                                 // 判重
                next.action = action_cur;                               // 记录路径
                next.father = state_hash(s);
                nodes[state_index(next)] = next;
                ++action_cur;                                           // return 前别忘了增 1
                return true;
            }
        }
        ++action_cur;
    }
    return false;
}

int bfs( state_t &start ) {
    queue<state_t> q;
    hashset_init();

    start.action = -1;
    start.father = -1;

    nodes[state_index(start)] = start;
    hashset_insert(start);
    if ( state_is_target(start) ) {
        return state_index(start);
    }

    q.push(start);
    while( !q.empty() ) {
        const state_t s = q.front(); q.pop();
        state_extend_init( s );
        state_t next;
        while( state_extend(s, next) ) {
            if( state_is_target(next) ) {       // the END
                return state_index(next);
            }
            q.push( next );
            hashset_insert( next );
        }
    }
    return -1;
}

int main(void) {
    for( int i = 0; i < m; ++i ) {
        for( int j = 0; j < n; ++j ) {
            scanf( "%d", &map[i][j] );
        }
    }

    state_t start = { 0, -1, -1 };                          // 左上角为起点
    int end = bfs( start );
    print_path( end );
    return 0;
}

C++ version @

#include <cstdio>
#include <queue>
#include <vector>
#include <stack>
#include <unordered_set>
#include <unordered_map>

using namespace std;

struct Point {
    int x, y;
    Point( int x = 0, int y = 0 ) : x(x), y(y) { }
    bool valid( const vector<vector<int>> &map ) const {
        return 0 <= x && x < map.size() && 0 <= y && y < map[0].size() && map.at(x).at(y) == 0;
    }
    bool operator==( const Point &rhs ) const {
        return x == rhs.x && y == rhs.y;
    }
};

namespace std {
    template <> struct hash<Point> {
        size_t operator()( const Point &p ) const {
            return p.x * 10 + p.y;
        }
    };
}

bool bfs( const vector<vector<int>> &map, unordered_map<Point, Point> &father, const Point &start, const Point &end ) {
    queue<Point> q;
    q.push( start );
    unordered_set<Point> s;
    s.insert( start );
    while( !q.empty() ) {
        Point p = q.front(); q.pop();
        static int dx[] = { 1, -1, 0,  0 };
        static int dy[] = { 0,  0, 1, -1 };
        for( int i = 0; i < 4; ++i ) {
            Point pp( p.x+dx[i], p.y+dy[i] );
            if( !pp.valid(map) || s.count(pp) ) { continue; }
            s.insert( pp );
            father[pp] = p;
            if( pp == end ) {
                return true;
            }
            q.push( pp );
        }
    }
    return false;
}

int main() {
    vector<vector<int>> map( 5, vector<int>(5) );
    for( int i = 0; i < 5; ++i ) {
        for( int j = 0; j < 5; ++j ) {
            scanf( "%d", &map[i][j] );
        }
    }
    Point start( 0, 0 );
    Point end  ( 4, 4 );
    unordered_map<Point, Point> father;
    if( bfs(map, father, start, end) ) {
        stack<Point> s;
        while( father.count(end) ) {
            s.push( end );
            end = father[end];
        }
        s.push( start );
        while( !s.empty() ) {
            printf("(%d, %d)\n", s.top().x, s.top().y );
            s.pop();
        }
    }
    return 0;
}

eight digit @

/* POJ 1077 Eight, http://poj.org/problem?id=1077 */
#include <cstdio>
#include <cstring>
#include <queue>

using namespace std;

const int DIGITS = 9; // 棋盘中数字的个数，也是变进制数需要的位数
const int MATRIX_EDGE = 3;       // 棋盘边长

/***** 一些常量 *****/
const int SPACE_NUMBER = 0; // 空格对应着数字 0
// 上下左右四个方向
const int dx[] = {-1, 1, 0, 0};
const int dy[] = {0, 0, -1, 1};
const char name[] = { 'u', 'd', 'l', 'r' };

typedef char int8_t;

/**
 * @strut 状态
 */
typedef struct state_t {
    int8_t data[DIGITS];  /** 状态的数据. */
    int action; /* 由父状态移动到本状态的动作 */
    int father; /* 父状态在 nodes[] 中的下标，也即父状态的哈希值 */
    int count;  /** 所花费的步骤数（也即路径长度 -1） */
} state_t;

// 3x3 的棋盘，状态最多有 9! 种
const int STATE_MAX = 362880;  /* 状态总数 */

state_t nodes[STATE_MAX+1];

int state_hash(const state_t &s) {
    return state_hash( &s );
}

int state_index(const state_t &s) {
    return state_hash(s);
}

/**
 * @brief 打印动作序列.
 * @param[in] end 终点状态的哈希值
 * @return 父状态
 */
void print_action(const int end) {
    if (nodes[end].father == -1) return;

    print_action(nodes[end].father);
    putchar(name[nodes[end].action]);
}

void hashset_init();

bool hashset_find(const state_t *s);

void hashset_insert(const state_t *s);

void state_extend_init(const state_t *s);

bool state_extend(const state_t *s, state_t *next);

bool state_is_target(const state_t *s);


int bfs(state_t *start) {
    queue<state_t> q;
    hashset_init();

    start->action = -1;
    start->father = -1;
    start->count = 0;

    nodes[state_index(*start)] = *start;
    hashset_insert(start);
    if (state_is_target(start))
        return state_index(*start);
    q.push(*start);

    while (!q.empty()) {
        const state_t s = q.front(); q.pop();
        state_t next;

        state_extend_init(&s);
        while (state_extend(&s, &next)) {
            if (state_is_target(&next)) {
                // printf("%d\n", next.count);
                return state_index(next);
            }
            q.push(next);
            hashset_insert(&next);
        }
    }
    return -1;
}

/**
 * @brief 输入.
 * @return 无
 */
void input(state_t *start) {
    int ch;
    for (int i = 0; i < DIGITS; ++i) {
        do {
            ch = getchar();
        } while ((ch != EOF) && ((ch < '1') || (ch > '8')) && (ch != 'x'));
        if (ch == EOF) return;
        if (ch == 'x') start->data[i] = 0; // x 映射成数字 0
        else           start->data[i] = ch - '0';
    }
}

/** for wikioi 1225 */
void input1(state_t *start) {
    int n;
    scanf("%d", &n);

    /* 将整数转化为棋盘 */
    for(int i = DIGITS-1; i >= 0; i--) {
        start->data[i] = n % 10;
        n /= 10;
    }
}

int main(void) {
    state_t start;
    int end; /* 目标状态在nodes[]中的下标 */
    input(&start);

    end = bfs(&start);

    print_action(end);
    printf("\n");
    return 0;
}

/********** functions implement **************/

/********** 方案1，完美哈希，使用康托展开 **************/

// 9 位变进制数（空格）能表示 0 到 (9!-1) 内的所有自然数, 恰好有 9! 个，
// 与状态一一对应，因此可以把状态一一映射到一个 9 位变进制数

// 9 位变进制数，每个位数的单位，0!~8!
const int fac[] = {40320, 5040, 720, 120, 24, 6, 2, 1, 1};
/* 哈希表容量，要大于状态总数，若存在完美哈希方案，则等于状态总数 */
const int HASH_CAPACITY = STATE_MAX;

bool visited[HASH_CAPACITY];

int state_hash(const state_t *s) {
    int key = 0;
    for (int i = 0; i < DIGITS; i++) {
        int cnt = 0;  /* 逆序数 */
        for (int j = i + 1; j < DIGITS; j++) if (s->data[i] > s->data[j]) cnt++;
        key += fac[i] * cnt;
    }
    return key;
}

void hashset_init() {
    memset(visited, 0, sizeof(visited));
}

bool hashset_find(const state_t *s) {
    return visited[state_hash(s)] == true;
}

void hashset_insert(const state_t *s) {
    visited[state_hash(s)] = true;
}

int action_cur;
#define ACTION_BEGIN 0
#define ACTION_END 4

/* 扩展点，即0的位置 */
int z;

void state_extend_init(const state_t *s) {
    action_cur = ACTION_BEGIN;
    for (z = 0; z < DIGITS; z++) {
        if (s->data[z] == SPACE_NUMBER) {
            break;  // 找 0 的位置
        }
    }
}

bool state_extend(const state_t *s, state_t *next) {
    const int x = z / MATRIX_EDGE; // 行
    const int y = z % MATRIX_EDGE; // 列

    while (action_cur < ACTION_END) {
        const int newx = x + dx[action_cur];
        const int newy = y + dy[action_cur];
        const int newz = newx * MATRIX_EDGE + newy;

        if (newx >= 0 && newx < MATRIX_EDGE && newy >= 0 &&
                newy < MATRIX_EDGE) { // 没有越界
            *next = *s;
            next->data[newz] = SPACE_NUMBER;
            next->data[z] = s->data[newz];
            next->count = s->count + 1;
            if (!hashset_find(next)) { /* 判重 */
                next->action = action_cur;
                next->father = state_hash(s);
                /* 记录路径 */
                nodes[state_index(*next)] = *next;
                action_cur++; /* return前别忘了增1 */
                return true;
            }
        }
        action_cur++;
    }
    return false;
}

// 目标状态
const state_t END = {{1, 2, 3, 4, 5, 6, 7, 8, 0}, -1, -1};
// for wikioi 1225
const state_t END1 = {{1, 2, 3, 8, 0, 4, 7, 6, 5}, -1, -1};

bool state_is_target(const state_t *s) {
    return memcmp(s->data, END.data, DIGITS * sizeof(int8_t)) == 0;
}

four go @

在一个 4 x 4 的棋盘上摆放了 14 颗棋子，其中有 7 颗白色棋子，7 颗黑色棋子，有两个空白地带，任何一颗黑白棋子都可以向上下左右四个方向移动到相邻的空格，这叫行棋一步，黑白双方交替走棋，任意一方可以先走，如果某个时刻使得任意一种颜色的棋子形成四个一线（包括斜线），这样的状态为目标棋局。

输入

    一个 4 x 4 的初始棋局，
    黑棋子用 B 表示，白棋子用 W 表示，空格地带用 O 表示。

    BWBO
    WBWB
    BWBW
    WBWO

输出

    移动到目标棋局的最少步数。

   5

分析

求最少步数，很自然的想到广搜。

如何表示一个状态？用一个二维数组 int board[4][4] 表示，还需要记录该状态是由白子还是黑子移动而导致的，走到该状态已经花费的步数。

如何扩展节点？每一步，从队列弹出一个状态，两个空格都可以向四个方向扩展，把得到的状态入队列。

如何判重？棋盘用二维矩阵存储，用 0 表示空格，1 表示黑色，2 表示白色，所以最后可以看成一个 16 位的三进制数。用这个数作为棋盘的编码，就可以用来判重了。注意，本题要黑白交替走，所以我们要区分状态是由白子还是黑子移动而导致的。

判重: visited[0] 记录白子的历史， visited[1] 记录黑子的历史

// std::map
map<int, bool> visited[2];

// 也可以开一个大数组当做哈希表，
#define HASH_MOD 43036875                       // hash表大小
bool visited[2][HASH_MOD];

C version @

/** wikioi 1004 四子连棋  , http://www.wikioi.com/problem/1004 */
#include <cstdio>
#include <cstring>
#include <queue>

using namespace std;

// 扩展的时候，先定空格，再定方向
// 记录当前方向，例如action_cur[0]记录了第一个空格，当前在扩展哪个方向
int action_cur[2];
#define ACTION_BEGIN 0
#define ACTION_END 4

typedef struct point_t {
    int x, y;
} point_t;
int space_cur;                          // 记录当前在扩展哪一个空格，值为0或1
point_t extend_pos[2];                  // 两个空格的位置

// 哈希表容量，要大于状态总数，若存在完美哈希方案，则等于状态总数
#define HASH_CAPACITY 43036875

bool visited[2][HASH_CAPACITY];
#define LEN 4                               // 边长
const int dx[] = { 1, -1, 0, 0 };           // 右，左，上，下（左下角为坐标原点）
const int dy[] = { 0, 0, 1, -1 };

typedef struct state_t {
    int board[LEN][LEN];                    // 棋局，1表示黑子，2表示白子，0表示空白
    int color;                              // 本状态是由白子还是黑子移动而导致的
    int count;                              // 所花费的步骤数（也即路径长度-1），求路径长度时需要
} state_t;

int state_hash(const state_t &s) {
    const static int RADIX = 3;         // 三进制
    int ret = 0;
    for (int i = 0; i < LEN; i++) {
        for (int j = 0; j < LEN; j++) {
            ret = ret * RADIX + s.board[i][j];
        }
    }
    return ret;
}

void hashset_init() {
    fill(visited[0], visited[0] + HASH_CAPACITY, false);
    fill(visited[1], visited[1] + HASH_CAPACITY, false);
}
bool hashset_find(const state_t &s) {
    return visited[s.color - 1][state_hash(s)] == true;
}
void hashset_insert(const state_t &s) {
    visited[s.color - 1][state_hash(s)] = true;
}
void state_extend_init(const state_t &s) {
    action_cur[0] = ACTION_BEGIN;
    action_cur[1] = ACTION_BEGIN;
    space_cur = 0;

    int k = 0;
    // 寻找两个空白的格子的位置
    for (int i = 0; i < LEN; i++) {
        for (int j = 0; j < LEN; j++) {
            if (s.board[i][j] == 0) {
                extend_pos[k].x = i;
                extend_pos[k].y = j;
                k++;
            }
        }
    }
}
bool state_extend(const state_t &s, state_t &next) {
    for (int i = 0; i < 2; i++) { /* 先第一个空格，再第二个空格 */
        while (action_cur[i] < ACTION_END) {
            const int x = extend_pos[i].x;
            const int y = extend_pos[i].y;
            int nextx = x + dx[action_cur[i]];
            int nexty = y + dy[action_cur[i]];
            next = s;
            next.count = s.count + 1;
            next.color = 3 - s.color;

            if (nextx >= 0 && nextx < LEN && nexty >= 0 &&
                nexty < LEN && next.color == s.board[nextx][nexty])     // 必须黑白交替走
            {
                // swap
                int temp = next.board[x][y];
                next.board[x][y] = next.board[nextx][nexty];
                next.board[nextx][nexty] = temp;

                if (!hashset_find(next)) { /* 判重 */
                    action_cur[i]++; /* return前别忘了增1 */
                    return true;
                }
            }
            action_cur[i]++;
        }
    }
    return false;
}

bool state_is_target(const state_t &s) {
    for (int i = 0; i < LEN; i++) {  /* 逐行检查 */
        int flag = 1;  /* 某一行全是同一颜色 */
        for (int j = 1; j < LEN; j++)
            if (s.board[i][j - 1] != s.board[i][j])
                flag = 0;
        if (flag)
            return 1;
    }
    for (int j = 0; j < LEN; j++) { //逐列检查
        int flag = 1;  /* 某一行全是同一颜色 */
        for (int i = 1; i < LEN; i++)
            if (s.board[i][j] != s.board[i - 1][j]) flag = 0;
        if (flag) return 1;
    }
    /* 斜线 */
    if (s.board[0][0] == s.board[1][1] && s.board[1][1] == s.board[2][2]
            && s.board[2][2] == s.board[3][3])
        return 1;
    if (s.board[0][3] == s.board[1][2] && s.board[1][2] == s.board[2][1]
            && s.board[2][1] == s.board[3][0])
        return 1;
    return 0;
}

void bfs(state_t &start) {
    queue<state_t> q;
    hashset_init();

    start.count = 0;
    start.color = 1;

    hashset_insert(start);
    q.push(start);

    start.color = 2;

    hashset_insert(start); // 千万别忘记了标记此处的访问记录
    if (state_is_target(start)) /* 如果起点就是终点，返回 */
        return;
    q.push(start);

    while (!q.empty()) {
        const state_t s = q.front(); q.pop();
        state_t next;

        state_extend_init(s);
        while (state_extend(s, next)) {
            if (state_is_target(next)) {
                printf("%d\n", next.count);
                return;
            }
            q.push(next);
            hashset_insert(next);
        }
    }
}

int main() {
    char s[LEN + 1];
    state_t start;

    for (int i = 0; i < LEN; i++) {
        scanf("%s", s);
        for (int j = 0; j < LEN; j++) {
            if (s[j] == 'B') start.board[i][j] = 1;
            else if (s[j] == 'W') start.board[i][j] = 2;
            else start.board[i][j] = 0;
        }
    }

    bfs(start);
    return 0;
}

C++ version @

// wikioi 1004 四子连棋  , http://www.wikioi.com/problem/1004
#include <cstdio>
#include <cstring>
#include <queue>
#include <unordered_set>

using namespace std;

struct state_t {
    int board[4][4], color, count;
    bool operator==( const state_t &rhs ) const {
        if( color != rhs.color ) { return false; }
        for( int i = 0; i < 4; ++i ) {
            for( int j = 0; j < 4; ++j ) {
                if( board[i][j] != rhs.board[i][j] ) {
                    return false;
                }
            }
        }
        return true;
    }
};

namespace std {
template<> struct hash<state_t> {
    size_t operator()( const state_t &x ) const {
        const static int RADIX = 3;
        int ret = 0;
        for( int i = 0; i < 4; ++i ) {
            for( int j = 0; j < 4; ++j ) {
                ret = ret * RADIX + x.board[i][j];
            }
        }
        return ret;
    }
};
}

class FourGo {
public:
    FourGo() { }
    unordered_set<state_t> visited[2];
    const static int ACTION_BEGIN = 0;
    const static int ACTION_END = 4;
    bool isVisited( const state_t &s ) { return visited[s.color - 1].count(s); }
    void insertState( const state_t &s ) { visited[s.color - 1].insert(s); }

    int action_cur[2];
    void state_extend_init(const state_t &s) {
        action_cur[0] = ACTION_BEGIN;
        action_cur[1] = ACTION_BEGIN;
        space_cur = 0;

        int k = 0;
        // 寻找两个空白的格子的位置
        for (int i = 0; i < 4; i++) {
            for (int j = 0; j < 4; j++) {
                if (s.board[i][j] == 0) {
                    extend_pos[k].x = i;
                    extend_pos[k].y = j;
                    k++;
                }
            }
        }
    }

    // 扩展的时候，先定空格，再定方向
    // 记录当前方向，例如action_cur[0]记录了第一个空格，当前在扩展哪个方向
    bool state_extend(const state_t &s, state_t &next) {
        const static int dx[4] = { 1, -1, 0, 0 };
        const static int dy[4] = { 0, 0, 1, -1 };
        for( int i = 0; i < 2; ++i ) {
            while (action_cur[i] < ACTION_END) {
                int x = extend_pos[i].x;
                int y = extend_pos[i].y;
                int nextx = x + dx[action_cur[i]];
                int nexty = y + dy[action_cur[i]];
                next = s;
                next.count = s.count + 1;
                next.color = 3 - s.color;

                ++action_cur[i];
                if ( 0 <= nextx && nextx < 4 && 0 <= nexty && nexty < 4
                  && next.color == s.board[nextx][nexty])     // 必须黑白交替走
                {
                    swap(next.board[x][y], next.board[nextx][nexty]);
                    if (!isVisited(next)) { return true; }
                }
            }
        }
        return false;
    }

    struct Point { int x, y; } extend_pos[2];
    int space_cur;
    bool isTarget( const state_t &s ) {
        bool okay;
        for (int i = 0; i < 4; i++) {
            okay = true;
            for (int j = 1; j < 4; j++) {
                if (s.board[i][j - 1] != s.board[i][j]) { okay = false; }
            }
            if (okay) { return true; }
        }
        for (int j = 0; j < 4; j++) {
            okay = true;
            for (int i = 1; i < 4; i++) {
                if (s.board[i][j] != s.board[i - 1][j]) { okay = false; }
            }
            if (okay) { return true; }
        }
        if ( (s.board[0][0] == s.board[1][1] && s.board[1][1] == s.board[2][2] && s.board[2][2] == s.board[3][3]) ||
             (s.board[0][3] == s.board[1][2] && s.board[1][2] == s.board[2][1] && s.board[2][1] == s.board[3][0]) ) { return true; }

        return false;
    }

    void bfs(state_t &start) {
        if(isTarget(start)) { return; }

        // init vis hash
        visited[0].clear();
        visited[1].clear();

        queue<state_t> q;

        start.count = 0;

        start.color = 1;
        insertState(start);
        q.push(start);

        start.color = 2;
        insertState(start);
        q.push(start);

        while (!q.empty()) {
            state_t s = q.front(); q.pop();
            state_t next;

            state_extend_init(s);
            while (state_extend(s, next)) {
                if (isTarget(next)) {
                    printf("%d\n", next.count);
                    return;
                }
                q.push(next);
                insertState(next);
            }
        }
    }
};

int main() {
    state_t start;
    FourGo fg;
    for (int i = 0; i < 4; i++) {
        char s[10];
        scanf("%s", s);
        for (int j = 0; j < 4; j++) {
            if (s[j] == 'B') start.board[i][j] = 1;
            else if (s[j] == 'W') start.board[i][j] = 2;
            else start.board[i][j] = 0;
        }
    }

    fg.bfs(start);
    return 0;
}

two-queue BFS (nothing here) @

See again. See Milo Yip’s blog post.
A* Algorithm (nothing here) :TODO: @

TODO
Conclusion @
- 适用场景 @
  
  输入数据：没什么特征，不像深搜，需要有“递归”的性质。如果是树或者图，概率更大。
  
  状态转换图：树或者图。
  
  求解目标：求最短。
- 思考的步骤 @
  
  是求路径长度，还是路径本身（或动作序列）？
  
  如果是求路径长度，则状态里面要存路径长度
  
  如果是求路径本身或动作序列
  
  要用一棵树存储宽搜过程中的路径
  
  是否可以预估状态个数的上限？能够预估状态总数，则开一个大数组，用树的双亲表示法；如果不能预估状态总数，则要使用一棵通用的树。这一步也是第4步的必要不充分条件。
  
  如何表示状态？ @
  
  即一个状态需要存储哪些些必要的数据，才能够完整提供如何扩展到下一步状态的所有信息。一般记录当前位置或整体局面。
  
  如何扩展状态？ @
  
  这一步跟第 2 步相关。状态里记录的数据不同，扩展方法就不同。对于固定不变的数据结构（一般题目直接给出，作为输入数据），如二叉树，图等，扩展方法很简单，直接往下一层走，对于隐式图，要先在第 1 步里想清楚状态所带的数据，想清楚了这点，那如何扩展就很简单了。
  
  关于判重，状态是否存在完美哈希方案？
  
  即将状态一一映射到整数，互相之间不会冲突。
  
  如果不存在，则需要使用通用的哈希表（自己实现或用标准库，例如 unordered_set）来判重；自己实现哈希表的话，如果能够预估状态个数的上限，则可以开两个数组，head 和 next，表示哈希表，参考第 subsec:eightDigits 节方案 2。
  
  如果存在，则可以开一个大布尔数组，作为哈希表来判重，且此时可以精确计算出状态总数，而不仅仅是预估上限。
  
  目标状态是否已知？ @
  
  如果题目已经给出了目标状态，可以带来很大便利，这时候可以从起始状态出发，正向广搜；也可以从目标状态出发，逆向广搜；也可以同时出发，双向广搜。
- 代码模板 @
  
  广搜需要一个队列，用于一层一层扩展，一个 hashset，用于判重，一棵树（只求长度时不需要），用于存储整棵树。
  
  对于队列，如果用纯 C，需要造一个队列轮子；如果用 C++，可以用 queue，也可以把 vector 当做队列使用。当求长度时，有两种做法：
  
  只用一个队列，但在状态结构体 state_t 里增加一个整数字段 step，表示走到当前状态用了多少步，当碰到目标状态，直接输出 step 即可。这个方案，可以很方便的变成 A* 算法，把队列换成优先队列即可。
  
  用两个队列，current, next，分别表示当前层次和下一层，另设一个全局整数 level，表示层数（也即路径长度），当碰到目标状态，输出 level 即可。这个方案，状态可以少一个字段，节省内存。
  
  对于 hashset，如果有完美哈希方案，用布尔数组 (bool visited[STATE_MAX] 或 vector<bool> visited(STATE_MAX, false)) 来表示；如果没有，可以用 STL 里的 set 或 unordered_set。
  
  对于树，如果用 STL，可以用 unordered_map<state_t, state_t> father 表示一颗树，代码非常简洁。如果能够预估状态总数的上限（设为 STATE_MAX），可以用数组(state_t nodes[STATE_MAX])，即树的双亲表示法来表示树，效率更高，当然，需要写更多代码。
  
  C++ template @
  
  template<typename state_t> vector<state_t> gen_path( const unordered_map<state_t, state_t> &father, const state_t &target) { vector<state_t> path; path.push_back(target); state_t cur = target; while (father.find(cur) != father.end()) { cur = father.at(cur); path.push_back(cur); } reverse(path.begin(), path.end()); return path; } /** * @brief 广搜. * @param[in] state_t 状态，如整数，字符串，一维数组等 * @param[in] start 起点 * @param[in] state_is_target 判断状态是否是目标的函数 * @param[in] state_extend 状态扩展函数 * @return 从起点到目标状态的一条最短路径 */ template<typename state_t> vector<state_t> bfs(state_t &start, bool (*state_is_target)(const state_t&), vector<state_t>(*state_extend)(const state_t&, unordered_set<string> &visited)) { queue<state_t> next, current; // 当前层，下一层 unordered_set<state_t> visited; // 判重 unordered_map<state_t, state_t> father; int level = 0; // 层次 bool found = false; state_t target; current.push(start); visited.insert(start); while (!current.empty() && !found) { ++level; while (!current.empty() && !found) { const state_t state = current.front(); current.pop(); vector<state_t> new_states = state_extend(state, visited); for (auto iter = new_states.begin(); iter != new_states.end() && ! found; ++iter) { const state_t new_state(*iter); if (state_is_target(new_state)) { found = true; //找到了 target = new_state; father[new_state] = state; break; } next.push(new_state); // visited.insert(new_state); 必须放到 state_extend()里 father[new_state] = state; } } swap(next, current); //!!! 交换两个队列 } if (found) { return gen_path(father, target); //return level + 1; } else { return vector<state_t>(); //return 0; } }
- C++ snippets ♥️ @
  
  struct State { bool operator==( const State &rhs ) const { return true; } bool operator<( const State &rhs ) const { return true; } }; namespace std { template<> struct hash<State> { size_t operator()( const State &s ) const { return 0; } }; } unordered_set<State> visited; priority_queue<State> pq;

chap10. DFS @
- four coloring @
  
  给定 N (N <= 8) 个点的地图，以及地图上各点的相邻关系，请输出用 4 种颜色将地图涂色的所有方案数（要求相邻两点不能涂成相同的颜色）。
  
  数据中 0 代表不相邻，1 代表相邻。
  
  输入第一行一个整数 N，代表地图上有 N 个点。接下来 N 行，每行 N 个整数，每个整数是 0 或者 1。第 i 行第 j列的值代表了第 i 个点和第 j 个点之间是相邻的还是不相邻，相邻就是 1，不相邻就是 0。我们保证 a[i][j] = a[j][i]。 8 0 0 0 1 0 0 1 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 输出染色的方案数 15552
  
  这是一道经典的题目。深搜。
  
  #include <cstdio> #include <vector> using namespace std; // 深搜，给第 cur 个节点涂色. void dfs( vector<vector<int> > &table, vector<int> &history, int cur, int N, int &count ) { if ( cur == N ) { ++count; return; } for ( int c = 1; c < 5; ++c ) { // try all possibilities // if okay, then go inside int j; for ( j = 0; j < cur; ++j ) { if ( table[cur][j] && c == history[j] ) { // 相邻且同色 break; } } if ( j == cur ) { // you can also use `ok' history[cur] = c; dfs( table, history, cur+1, N, count ); } } } int main() { int N; scanf( "%d", &N ); vector<vector<int> > table(N, vector<int>(N)); for ( int i = 0; i < N; ++i ) { for ( int j = 0; j < N; ++j ) { scanf( "%d", &table[i][j] ); } } int count = 0; vector<int> history(N); // 记录每个点的颜色，四种颜色用1234表示，0表示未染色 dfs( table, history, 0, N, count ); printf( "%d\n", count ); return 0; }
- all arrangements (dup)
- eight queen (dup)
- restore IP addr @
  
  本题是 LeetCode Online Judge上的“Restore IP Addresses”。
  
  给定一个只包含数字的字符串，还原出所有合法的IP地址。
  
  例如：给定 “25525511135”，返回 ["255.255.11.135", "255.255.111.35"]。 (顺序无关紧要)
  
  这题很明显分为四步，有层次，因此可以尝试用回溯法解决。
  
  // LeetCode, Restore IP Addresses class Solution { public: vector<string> restoreIpAddresses(string s) { vector<string> result; string ip; // 存放中间结果 dfs( s, 0, 0, ip, result ); return result; } void dfs( string s, int start, int step, string ip, vector<string> &result ) { if ( s.size() - start > (4 - step) * 3 || s.size() - start < (4 - step) ) { return; } // 非法结果，剪枝 if (start == s.size() && step == 4) { // 找到一个合法解 ip.resize(ip.size() - 1); result.push_back(ip); return; } int num = 0; for ( int i = start; i < start + 3; ++i ) { num = num * 10 + (s[i] - '0'); if( num <= 255 ) { // 当前结点合法，则继续往下递归 ip += s[i]; dfs( s, i+1, step+1, ip+'.', result ); } if ( num == 0 ) break; // 不允许前缀 0，但允许单个0 } } };
- combination sum @
  
  本题是 LeetCode Online Judge 上的 “Combination Sum”。
  
  给定一个数的集合 (C) 和一个目标数 (T)，找到 C 中所有不重复的组合，让这些被选出来的数加起来等于 T。
  
  每一个数可以被选无数次。
  
  注意：
  
  所有的数（包括目标）都是正整数
  
  一个组合（a₁, a₂, …, a_k）中的元素必须以非递减顺序排列
  
  一个组合不能与另一个组合重复
  
  例如，给定一组数 2,3,6,7, 和目标 7，则答案是
  
  [7] [2, 2, 3]
  
  这题没有固定的步骤数，但是步骤也是有限的，因此可以尝试用回溯法。
  
  class Solution { public: vector<vector<int> > combinationSum(vector<int> &nums, int target) { sort(nums.begin(), nums.end()); vector<vector<int> > result; // 最终结果 vector<int> cur; // 中间结果 dfs(nums, target, 0, cur, result); return result; } private: void dfs( vector<int> &nums, int gap, int level, vector<int> &cur, vector<vector<int>> &result ) { if( gap == 0 ) { // 找到一个合法解 result.push_back( cur ); return; } int n = nums.size(); for( int i = level; i < n; ++i ) { // 扩展状态 if( gap < nums[i] ) { return; } // 剪枝 cur.push_back( nums[i] ); // 执行扩展动作 dfs(nums, gap - nums[i], i, cur, result); cur.pop_back(); // 撤销动作 } } };
- combination sum ii @
  
  本题与上一题唯一不同的是，每个数只能使用一次。
  
  // LeetCode, Combination Sum II class Solution { public: vector<vector<int> > combinationSum2( vector<int> &nums, int target ) { sort( nums.begin(), nums.end() ); vector<vector<int> > result; vector<int> cur; dfs( nums, target, 0, cur, result ); return result; } private: // 使用 nums[index, nums.size()) 之间的元素，能找到的所有可行解 static void dfs( vector<int> &nums, int gap, int index, vector<int> &cur, vector<vector<int> > &result ) { if( gap == 0 ) { // 找到一个合法解 result.push_back(cur); return; } int previous = nums[0]-1; // so will not dup int n = nums.size(); for( int i = index; i < n; ++i ) { // 如果上一轮循环选 nums[i]，则本次循环就不能再选 nums[i]， // 确保nums[i] 最多只用一次 if( previous == nums[i] ) { continue; } if( gap < nums[i] ) { return; } // 剪枝 previous = nums[i]; cur.push_back( nums[i] ); dfs( nums, gap - nums[i], i + 1, cur, result); cur.pop_back(); } } };
- conclusion ♥️ @
  
  输入数据
  
  如果是递归数据结构，如单链表，二叉树，集合，则百分之百可以用深搜；如果是非递归数据结构，如一维数组，二维数组，字符串，图，则概率小一些。
  
  状态转换图
  
  树或者图。
  
  求解目标
  
  必须要走到最深（例如对于树，必须要走到叶子节点）才能得到一个解，这种情况适合用深搜。
  
  思考的步骤
  
  是求路径条数，还是路径本身（或动作序列）？深搜最常见的三个问题，求可行解的总数，求一个可行解，求所有可行解。
  
  如果是求路径本身，则要用一个数组 path[] 存储路径。跟宽搜不同，宽搜虽然最终求的也是一条路径，但是需要存储扩展过程中的所有路径，在没找到答案之前所有路径都不能放弃；而深搜，在搜索过程中始终只有一条路径，因此用一个数组就足够了。
  
  如果是路径条数，则不需要存储路径。
  
  只要求一个解，还是要求所有解？如果只要求一个解，那找到一个就可以返回；如果要求所有解，找到了一个后，还要继续扩展，直到遍历完。广搜一般只要求一个解，因而不需要考虑这个问题（广搜当然也可以求所有解，这时需要扩展到所有叶子节点，相当于在内存中存储整个状态转换图，非常占内存，因此广搜不适合解这类问题）。
  
  如何表示状态？即一个状态需要存储哪些些必要的数据，才能够完整提供如何扩展到下一步状态的所有信息。跟广搜不同，深搜的惯用写法，不是把数据记录在状态 struct 里，而是添加函数参数（有时为了节省递归堆栈，用全局变量），struct 里的字段与函数参数一一对应。
  
  如何扩展状态？这一步跟上一步相关。状态里记录的数据不同，扩展方法就不同。对于固定不变的数据结构（一般题目直接给出，作为输入数据），如二叉树，图等，扩展方法很简单，直接往下一层走，对于隐式图，要先在第1步里想清楚状态所带的数据，想清楚了这点，那如何扩展就很简单了。
  
  关于判重
  
  如果状态转换图是一棵树，则不需要判重，因为在遍历过程中不可能重复。
  
  如果状态转换图是一个图，则需要判重，方法跟广搜相同，见第 bfs-template 节。这里跟第 8 步中的加缓存是相同的，如果有重叠子问题，则需要判重，此时加缓存自然也是有效果的。
  
  终止条件是什么？
  
  终止条件是指到了不能扩展的末端节点。对于树，是叶子节点，对于图或隐式图，是出度为 0 的节点。
  
  收敛条件是什么？
  
  收敛条件是指找到了一个合法解的时刻。如果是正向深搜（父状态处理完了才进行递归，即父状态不依赖子状态，递归语句一定是在最后，尾递归），则是指是否达到目标状态；如果是逆向深搜（处理父状态时需要先知道子状态的结果，此时递归语句不在最后），则是指是否到达初始状态。
  
  由于很多时候终止条件和收敛条件是是合二为一的，因此很多人不区分这两种条件。仔细区分这两种条件，还是很有必要的。
  
  为了判断是否到了收敛条件，要在函数接口里用一个参数记录当前的位置（或距离目标还有多远）。如果是求一个解，直接返回这个解；如果是求所有解，要在这里收集解，即把第一步中表示路径的数组 path[] 复制到解集合里。}
  
  如何加速？
  
  剪枝。深搜一定要好好考虑怎么剪枝，成本小收益大，加几行代码，就能大大加速。这里没有通用方法，只能具体问题具体分析，要充分观察，充分利用各种信息来剪枝，在中间节点提前返回。
  
  缓存。如果子问题的解会被重复利用，可以考虑使用缓存。
  
  前提条件：子问题的解会被重复利用，即子问题之间的依赖关系是有向无环图 (DAG)。如果依赖关系是树状的（例如树，单链表），没必要加缓存，因为子问题只会一层层往下，用一次就再也不会用到，加了缓存也没什么加速效果。
  
  具体实现：可以用数组或 HashMap。维度简单的，用数组；维度复杂的，用 HashMap，C++ 有 map，C++ 11 以后有 unordered_map，比 map 快。
  
  拿到一个题目，当感觉它适合用深搜解决时，在心里面把上面 8 个问题默默回答一遍，代码基本上就能写出来了。对于树，不需要回答第 5 和第 8 个问题。如果读者对上面的经验总结看不懂或感觉“不实用”，很正常，因为这些经验总结是笔者做了很多深搜题后总结出来的，从思维的发展过程看，“经验总结”要晚于感性认识，所以这时候建议读者先做做后面的题目，积累一定的感性认识后，在回过头来看这一节的总结，相信会和笔者有共鸣。
  
  代码模板 @
  
  // @param[in] input 输入数据指针 // @param[inout] cur or gap 标记当前位置或距离目标的距离 // @param[out] path 当前路径，也是中间结果 // @param[out] result 存放最终结果 // @return 路径长度，如果是求路径本身，则不需要返回长度 // void dfs(type *input, type *path, int cur or gap, type *result) { if (数据非法) return 0; // 终止条件 if (cur == input.size( or gap == 0)) { // 收敛条件将path放入result } if (可以剪枝) return; for(...) { // 执行所有可能的扩展动作执行动作，修改path dfs(input, step + 1 or gap--, result); 恢复path } }
  
  深搜与回溯法的区别
  
  回溯法 = 深搜 + 剪枝。一般大家用深搜时，或多或少会剪枝，因此深搜与回溯法没有什么不同，可以在它们之间画上一个等号。本书同时使用深搜和回溯法两个术语，但读者可以认为二者等价。
  
  深搜一般用递归 (recursion) 来实现，这样比较简洁。
  
  深搜能够在候选答案生成到一半时，就进行判断，抛弃不满足要求的答案，所以深搜比暴力搜索法要快。
  
  深搜与递归的区别
  
  深搜经常用递归 (recursion) 来实现，二者常常同时出现，导致很多人误以为他俩是一个东西。
  
  深搜，是逻辑意义上的算法，递归，是一种物理意义上的实现，它和迭代 (iteration) 是对应的。深搜，可以用递归来实现，也可以用栈来实现；而递归，一般总是用来实现深搜。可以说，递归一定是深搜，深搜不一定用递归。
  
  递归有两种加速策略，一种是剪枝 (prunning)，对中间结果进行判断，提前返回；一种是加缓存（就变成了 memoization，备忘录法），缓存中间结果，防止重复计算，用空间换时间。
  
  其实，递归 + 缓存，就是一种 memorization 。所谓memorization（备忘录法），就是 “top-down with cache”（自顶向下 + 缓存），它是 Donald Michie 在 1968 年创造的术语，表示一种优化技术，在 top-down 形式的程序中，使用缓存来避免重复计算，从而达到加速的目的。
  
  memorization 不一定用递归，就像深搜不一定用递归一样，可以在迭代 (iterative) 中使用 memorization 。递归也不一定用 memorization，可以用 memorization 来加速，但不是必须的。只有当递归使用了缓存，它才是 memorization 。
  
  既然递归一定是深搜，为什么很多书籍都同时使用这两个术语呢？在递归味道更浓的地方，一般用递归这个术语，在深搜更浓的场景下，用深搜这个术语，读者心里要弄清楚他俩大部分时候是一回事。在单链表、二叉树等递归数据结构上，递归的味道更浓，这时用递归这个术语；在图、隐士图等数据结构上，递归的比重不大，深搜的意图更浓，这时用深搜这个术语。

✂️ 2016/08/13 上午 9:30:00 4. 动态规划 Dynamic Programming I @

什么是动态规划？动态规划的意义是什么？ @
动态规划（Dynamic programming）中递推式的求解方法不是动态规划的本质。

动态规划的本质，是对问题【状态】的定义和【状态转移方程】的定义。

引自维基百科

dynamic programming is a method for solving a complex problem by breaking it down into a collection of simpler subproblems.

动态规划是通过拆分问题，定义问题状态和状态之间的关系，使得问题能够以递推（或者说分治）的方式去解决。本题下的其他答案，大多都是在说递推的求解方法，但如何拆分问题，才是动态规划的核心。而拆分问题，靠的就是状态的定义和状态转移方程的定义。
动态规划迷思
“缓存（memoization）”，“重叠子问题（subproblems）”，“记忆化”： @

这三个名词，都是在阐述递推式求解的技巧。以 Fibonacci 数列为例，计算第 100 项的时候，需要计算第 99 项和 98 项；在计算第 101 项的时候，需要第 100 项和第 99 项，这时候你还需要重新计算第 99 项吗？不需要，你只需要在第一次计算的时候把它记下来就可以了。

上述的需要再次计算的“第 99 项”，就叫“重叠子问题”。如果没有计算过，就按照递推式计算，如果计算过，直接使用，就像“缓存”一样，这种方法，叫做“记忆化”，这是递推式求解的技巧。这种技巧，通俗的说叫“花费空间来节省时间”。都不是动态规划的本质，不是动态规划的核心。

“递归” @

递归是递推式求解的方法，连技巧都算不上。

“无后效性”，“最优子结构” @

上述的状态转移方程中，等式右边不会用到下标大于左边 i 或者 k 的值，这是“无后效性”的通俗上的数学定义，符合这种定义的状态定义，我们可以说它具有“最优子结构”的性质，在动态规划中我们要做的，就是找到这种“最优子结构”。
文艺的说，动态规划是寻找一种对问题的观察角度，让问题能够以递推（或者说分治）的方式去解决。寻找看问题的角度，才是动态规划中最耀眼的宝石！

另一个回答：
- 一个阶段的最优可以由前一个阶段的最优得到。
- 如果一个阶段的最优无法用前一个阶段的最优得到呢？
刚刚的情况实在太普遍，解决方法实在太暴力，有没有哪些情况可以避免如此的暴力呢？

契机就在于后效性。

有一类问题，看似需要之前所有的状态，其实不用。不妨也是拿最长上升子序列的例子来说明为什么他不必需要暴力搜索，进而引出动态规划的思路。（这其实是说你要仔细区分状态，那些是无所谓的状态，哪些是本质的必须要留意的状态。这也和上面的正确选择【状态】的定义一个意思。）

这就可以纵容我们不需要记录之前所有的状态啊！既然我们的选择已经不受之前状态的组合的影响了，那时间复杂度自然也不是指数的了啊！虽然我们不在乎某序列之前都是什么元素，但我们还是需要这个序列的长度的。所以我们只需要记录以某个元素结尾的 LIS 长度就好！因此第 i 个阶段的最优解只是由前 i-1 个阶段的最优解得到的，然后就得到了 DP 方程：

LIS(i) = max{ LIS(j)+1 } for j<i & a[j] < a[i]

所以一个问题是该用递推、贪心、搜索还是动态规划，完全是由这个问题本身阶段间状态的转移方式决定的！
- 每个阶段只有一个状态 -> 递推；
- 每个阶段的最优状态都是由上一个阶段的最优状态得到的 -> 贪心；
- 每个阶段的最优状态是由之前所有阶段的状态的组合得到的 -> 搜索；
- 每个阶段的最优状态可以从之前某个阶段的某个或某些状态直接得到而不管之前这个状态是如何得到的 -> 动态规划。
每个阶段的最优状态可以从之前某个阶段的某个或某些状态直接得到

这个性质叫做最优子结构（optimal substructure）；

而不管之前这个状态是如何得到的

这个性质叫做无后效性。（历史不对未来产生深远影响。）

动态规划最重要的就是理解【最优原理】：如果一个决策的前面若干步骤已经确定从而进入某种状态之后，后面的步骤从按照当前状态开始的最优解必然是整体（包括该状态的情况下）的最优解，则该问题满足最优原理。换句话说，在求解（整体问题）的最优解的时候，后面的步骤选择只与当前状态有关，而【与如何到达这个状态的步骤无关】。

问题满足最优原理之后，我们可以把某个状态到目标的最优解记录下来，这样当通过不同的步骤走到相同的状态的时候，就不需要重复搜索了，有一些问题还可以推出递推公式进行求解。

设计动态规划算法的时候，最核心的就是如何【设计状态】，使得状态的可能性尽量少，却又同时满足最优原理。例如，如果状态被设置为所有到达该状态步骤组成，显然符合最有原理，但这就和原来的问题一样了，并没有让问题更简单。

最后，动态规划算法和广度优先搜索解决的是同样的问题，解决问题的方法的描述方式不同而已。
对动态规划（Dynamic Programming）的理解：从穷举开始 @

TODO

《算法竞赛入门经典 (豆瓣)》中 LiuRuJia 是按“穷举－分治－dp” 来安排书本章节的，这并非偶然，要深入理解并灵活运用 dp 必须要先对穷举和分治有很好的基础。否则就会陷入 LRJ 指出的一种现象：

“每次碰到新题自己都想不出来，但一看题解就懂”的尴尬情况。

动态规划 - 华科小涛 @

TODO

最近在看算法导论：上面讲的不错：当问题具有最优子结构和重叠子问题时，可以考虑用动态规划算法。动态规划方法安排求解顺序，对每个子问题只求解一次，并将结果保存下来。如果随后再次需要此子问题的解，只需查找保存的结果，而不必重新计算。因此动态规划算法是付出额外的内存空间来节省计算时间，是典型的时空权衡的例子。

如何理解动态规划？ @
贪心：【每一步只选最优】 +----H----+ +----P----+ / \ / \ A -+ +----O----+ +-- Z \ / \ / +----I----+ +----Q----+ min(H,I) min(P,Q) 穷举：【把这些路都尝试一遍，才知道哪个最优】 A --+-- H ----- P -------- Z | \ / | +---- Q -------/ | / +-- I ----- R -----/ \ / +----- S --+ 动态规划：【暴力，但 A-H-Q 和 A-I-Q 保存一条就可以了】 -- P -- / \ -- H -+ \ / \ \ A -+ -- Q -----+-- Z \ / / -- I -+ / \ / -- R --

最后用经典的 0-1 背包问题做个例子，巩固一下吧，这个任务是，我们从 N 个物品选若干塞到可以承受最大重量 W 的包包里面，要价值最大，因此就可以将任务分成 N 个步骤，每个步骤面对第 i 号物品，决策有两条：选，还是放弃，这里的状态，就是影响之后步骤决策的因素，在这里，就是“背包的剩余空间”

比如，物品的重量是 1,2,3,4,5,6，W=12，从头决策，0 表示放弃，1 表示选， BFS 三次后有八种状态：

  000 剩12
  001 剩9
  ……（略）
  110 剩9
  ……（略）

前三次步骤后，001 和 110 到达了同样的状态，都是剩余可装重量 9 的东西，这样在剩下的决策中，这俩分支走的路都是一样的，跟你之前是选了 001 还是 110 没有任何关系（无后效性），因此只要看 001 价值大，还是 110 价值大就可以了，8 个状态减少为 7 个，继续 BFS 下去，每一轮都合并同样状态，完成后，从最后一轮的所有状态中，找到价值最大的就 ok 了

由于状态最多有 W+1 个，进行 N 轮，因此复杂度 O(NW)，书上说的状态迁移方程的办法其实跟这个过程很类似，不过对于有些题目，比起 BFS+ 状态合并，状态方程的分析可以做更好的优化，如引入单调队列什么的，但 BFS+ 状态合并可以让你得到一个没有追求极限但是也比较快的解决方案了，结合具体问题有时候更适合，比如根据问题的实际需求，搜索可以限界剪枝减少工作量，我在工作中就用过，替换了同事从 wiki 抄的 DP 算法，效率能提升一些

最后留个小题，是以前做考官时候经常用的一道面试题，印象中有算法基础的同学六七成都能立即说“用 DP”，然而一问状态转移就晕了 ^_^：在约定的规则下，以数字数组的形式输入一手斗地主的牌，设计算法计算这手牌最少几把可以出完注意这里只是用斗地主做个例子，不代表牌数限制为 20 张，可以看做是一个 N 个数字根据规则分组的问题，说斗地主是因为之前是做游戏行业的，而且面试时候这样说比较容易降低同学们的紧张度，同时也是一个暗示：大家都知道斗地主靠贪心法是得不到最优出牌顺序的吧，哈。。。
refs and see also
Dynamic programming @
Sometimes, applying memoization to the naive recursive algorithm (namely the one obtained by a direct translation of the problem into recursive form) already results in a dynamic programming algorithm with asymptotically optimal time complexity, but for optimization problems in general the optimal algorithm might require more sophisticated algorithms. Some of these may be recursive (and hence can be memoized) but parametrized differently from the naive algorithm. For other problems the optimal algorithm may not even be a memoized recursive algorithm in any reasonably natural sense. An example of such a problem is the Egg Dropping puzzle described below.

Figure 1. Finding the shortest path in a graph using optimal substructure; a straight line indicates a single edge; a wavy line indicates a shortest path between the two vertices it connects (other nodes on these paths are not shown); the bold line is the overall shortest path from start to goal.

Fibonacci 序列的子问题示意图：使用有向无环图（DAG, directed acyclic graph）而非树表示重复子问题的分解。为什么是 DAG 而不是树呢？答案就是，如果是树的话，会有很多重复计算，下面有相关的解释。

为避免重复计算，可将已经得到的子问题的解保存起来，当我们要解决相同的子问题时，重用即可。该方法即所谓的缓存（memoization，而不是存储 memorization，虽然这个词亦适合，姑且这么叫吧，这个单词太难翻译了，简直就是可意会不可言传，其意义是没计算过则计算，计算过则保存）。当我们确信将不会再需要某一解时，可以将其抛弃，以节省空间。在某些情况下，我们甚至可以提前计算出那些将来会用到的子问题的解。
```
var m := map(0 → 0, 1 → 1)
function fib(n)
    if key n is not in map m
        m[n] := fib(n − 1) + fib(n − 2)
    return m[n]
```
This technique of saving values that have already been calculated is called 【memoization】;

refs and see also
动态规划算法的适用条件 @
必须满足如下三点：
- 最优化原理：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构（optimal substructure），即满足最优化原理。
- 无后效性：即某阶段状态一旦确定，就不受这个状态以后决策的影响。也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关。
- 有重叠子问题（overlapping subproblem）：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。（该性质并不是动态规划适用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势）
refs and see also
- 动态规划的适用条件 - 和申的日志 - 网易博客
动态规划算法的四个解题要素 ♥️ @
作为 Sia 粉（Sia Furler），我把它记作 sfia。
- 状态 State
  
  灵感，创造力，存储小规模问题的结果
- 方程 Function
  
  状态之间的联系，怎么通过小的状态，来算大的状态
- 初始化 Initialization
  
  最极限的小状态是什么, 起点
- 答案 Answer
  
  最大的那个状态是什么，终点
动规的两种实现方式：记忆化搜索 (top-down) vs 循环递推 (bottom-up)
面试中动态规划的常见类型 @
满足下面三个条件之一：
- 求最大值、最小值
- 判断是否可行
- 统计方案个数
则极有可能是使用动态规划求解
什么情况下不使用动态规划？
满足下面三个条件之一：

求出所有具体的方案而非方案个数 http://www.lintcode.com/problem/palindrome-partitioning/

输入数据是一个集合而不序列 http://www.lintcode.com/problem/longest-consecutive-sequence/

暴力的算法已经是多项式级别，2ⁿ → n² 是 DP 擅长的事

则极不可能使用动态规划求解

leetcode 中几道动态规划题 @

Triangle @

Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.

For example, given the following triangle

[
     [2]
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).

Note:

Bonus point if you are able to do this using only O(n) extra space, where n is the total number of rows in the triangle.

    类似于图像处理里的【直方图 vs. 累计直方图】，概率论里的【PDF，CDF】：

      [2]                                      [2=2]
     [3,4],                            [ 5 =(2+3), 6 =(2+4) ]
    [6,5,7],                      [ 11 =(5+6),  10 =(5+5 )   13 =(6+7) ]
   [4,1,8,3]                  [   15         11        18          16       ]
                                              ^
                                              |
                                              +----got you

从下往上看呢？

      | j = 0   1   2   3
------+------------------------------------------------------------------------------
i = 0 |     2               |                   |                   |   11
    1 |     3   4           |                   |   9   10          |   9   10
    2 |     6   5   7       |   7   6   10      |   7   6   10      |   7   6   10
    3 |     4   1   8   3   |   4   1   8   3   |   4   1   8   3   |   4   1   8   3

首先，定义状态转移方程：

f(i,j) = min{
                    f(i+i,j),
                    f(i+1,j+1)
            }                       +       f(i,j),
                                                            for j = 0..i, i = n-2..0

int minimumTotal( vector<vector<int>> &triangle ) {
    for( int i = triangle.size() -2; i >= 0; --i ) {
        for( int j = 0; j < i+1; ++j ) {
            vector<vector<int>> &t = triangle;                  // save some typing
            t[i][j] += min(t[i+1][j], t[i+1][j+1]);
        }
    }
    return triangle[0][0];
}

refs and see also

Triangle | LeetCode OJ

Maximum Subarray @
Find the contiguous subarray within an array (containing at least one number) which has the largest sum.

For example, given the array [−2,1,−3,4,−1,2,1,−5,4], the contiguous subarray [4,−1,2,1] has the largest sum = 6.

贯序地看，对于新加入数组的一个元素，我们有【两种选择】：
- 加入原来的 sub array，
- 新生成一个 sub array（原来的 sub array 为负）
S[n] 为序列，S[j] 为第 j 个元素（1 based）。设状态 f[j] 表示以 S[j] 结尾的最大连续子序列和，则状态转移方程如下：
- f[j] = max( f[j-1]+S[j], S[j] ), j = 2..n, f = S
- target = max{ f[j] }, j = 1..n
代码：
```
// Time: O(n), Space: O(1)
int maxSubArray( vector<int> &nums ) {
    int result = INT_MIN, f = 0;
    for( int i = 0; i < nums.size(); ++i ) {
        f = max( f+nums[i], nums[i] );
        result = max( f, result );
    }
    return result;
}
```
感兴趣的读者请参考这篇博客 http://www.cnblogs.com/gj-Acit/archive/2013/02/12/2910332.html

refs and see also
- Maximum Subarray | LeetCode OJ

Minimum Path Sum @

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

状态转移方程： f[i][j] = min(f[i-1][j], f[i][j-1]) + grid(i,j)

备忘录法 (top-down) @

class Solution {
public:
    int minPathSum( vector<vector<int>> &grid ) {
        const int m = grid.size();
        const int n = grid[0].size();
        f = vector<vector<int>>( m, vector<int>(n, -1) );
        return dfs( grid, m-1, n-1 );
    }
private:
    vector<vector<int>> f;                          // 缓存

    int dfs( const vector<vector<int>> &grid, int x, int y ) {
        if( x < 0 || y < 0 )    { return INT_MAX; }
        if( x == 0 && y == 0 )  { return grid[0][0]; }
        return min( getOrUpdate(grid, x-1, y), getOrUpdate(grid, x, y-1) ) + grid[x][y];
    }
    int getOrUpdate( const vector<vector<int>> &grid, int x, int y ) {
        if( x < 0 || y < 0 )    { return INT_MAX; }
        if( f[x][y] >= 0 ) {
            return f[x][y];
        } else {
            return f[x][y] = dfs(grid,x,y);
        }
    }
};

动态规划 (bottom-up) @

??? works???

int minPathSum( vector<vector<int>> &grid ) {
    const int m = grid.size();
    const int n = grid[0].size();
    int f[m][n];
    f[0][0] = grid[0][0];
    for( int i = 1; i < m; ++i ) {
        f[i][0] = f[i-1][0] + grid[i][0];
    }
    for( int j = 1; j < n; ++j ) {
        f[0][j] = f[0][j-1] + grid[0][j];
    }
    for( int i = 1; i < m; ++i ) {
        for( int j = 1; j <n; ++j ) {
            f[i][j] = min( f[i-1][j], f[i][j-1] ) + grid[i][j];
        }
    }
    return f[m-1][n-1];
}

动态规划 + 滚动数组 @

Works???

int minPathSum( vector<vector<int>> &grid ) {
    const int m = grid.size();
    const int n = grid[0].size();

    int f[n];
    fill( f, f+n, INT_MAX );                    // !!! important
    f[0] = 0;                                   // not grid[0][0]

    for( int i = 0; i < m; ++i ) {
        f[0] += grid[i][0];
        for( int j = 1; j < n; ++j ) {
            f[j] = min( f[j-1], f[j] ) + grid[i][j];
        }
    }
    return f[n-1];
}

refs and see also

Minimum Path Sum | LeetCode OJ

面试中常见的动态规划类型 @
- 坐标型动态规划 15%
  - state:
    
    f[x] 表示我从起点走到坐标 x……
    
    f[x][y] 表示我从起点走到坐标 x,y……
  - function: 研究走到 x,y 这个点之前的一步
  - initialize: 起点
  - answer: 终点
- 序列型动态规划 30%
  - state: f[i] 表示前 i 个位置 / 数字 / 字符, 第 i 个…
  - function: f[i] = f[j] … j 是 i 之前的一个位置
  - initialize: f..
  - answer: f[n]..
    
    一般 answer 是 f(n) 而不是 f(n-1)
    
    因为对于 n 个字符, 包含前 0 个字符 (空串), 前 1 个字符…… 前 n 个字符。
- 双序列动态规划 30%
- 划分型动态规划 10%
- 背包型动态规划 10%
- 区间型动态规划 5%
如果不是跟坐标相关的动态规划, 一般有 N 个数 / 字符, 就开 N+1 个位置的数组, 第 0 个位置单独留出来作初始化
dp and memoization

Longest Consecutive Sequence @

左右扩张。

TODO

class Solution {
public:
    int longestConsecutive(vector<int> &num) {
        int r = 0;
        unordered_set<int> s;
        for (auto i: num)
            s.insert(i);
        for (auto i: num) {
            int j = i, k = i+1;
            while (s.count(j-1)) s.erase(--j);  // j--?
            while (s.count(k)) s.erase(k++);
            r = max(r, k-j);
        }
        return r;
    }
};

refs and see also

Longest Consecutive Sequence | LeetCode OJ

longest common subseq
longest consequtive common subseq
long M subseq
backpack

Word Break ♥️ @

Given a string s and a dictionary of words dict, determine if s can be segmented into a space-separated sequence of one or more dictionary words. For example, given s = “leetcode”, dict = [“leet”, “code”]. Return true because “leetcode” can be segmented as “leet code”.

java code:

public class Solution {
    private int getMaxLength(Set<String> dict) {
        int maxLength = 0;
        for (String word : dict) {
            maxLength = Math.max(maxLength, word.length());
        }
        return maxLength;
    }

    public boolean wordBreak(String s, Set<String> dict) {
        if (s == null || s.length() == 0) {
            return true;
        }

        int maxLength = getMaxLength(dict);
        boolean[] canSegment = new boolean[s.length() + 1];

        canSegment = true;
        for (int i = 1; i <= s.length(); i++) {
            canSegment[i] = false;
            for (int lastWordLength = 1;
                     lastWordLength <= maxLength && lastWordLength <= i;
                     lastWordLength++) {
                if (!canSegment[i - lastWordLength]) {
                    continue;
                }
                String word = s.substring(i - lastWordLength, i);
                if (dict.contains(word)) {
                    canSegment[i] = true;
                    break;
                }
            }
        }

        return canSegment[s.length()];
    }
}

state: f[i] 表示“前 i”个字符能否被完美切分
function: f[i] = OR{f[j] && j+1~i is a word}, 其中 j < i
initialize: f = true
answer: f[n]

注意: 切分位置的枚举 ->单词长度枚举 O(NL²), N: 字符串长度, L: 最长的单词的长度

refs and see also

Word Break 参考程序 Java/C++/Python

Palindrome Partitioning @

Given a string s, partition s such that every substring of the partition is a palindrome.

Return all possible palindrome partitioning of s.

For example, given s = “aab”, Return

[
  ["aa","b"],
  ["a","a","b"]
]

深搜 1 @

// 时间复杂度 O(2^n)，空间复杂度 O(n)
class Solution {
public:
    vector<vector<string>> partition(string s) {
        vector<vector<string>> result;
        vector<string> path;  // 一个partition方案
        dfs(s, path, result, 0, 1);
        return result;
    }

    // prev 表示前一个隔板, start 表示当前隔板
    void dfs(string &s, vector<string>& path,
            vector<vector<string>> &result, size_t prev, size_t start) {
        if (start == s.size()) { // 最后一个隔板
            if (isPalindrome(s, prev, start - 1)) { // 必须使用
                path.push_back(s.substr(prev, start - prev));
                result.push_back(path);
                path.pop_back();
            }
            return;
        }
        // 不断开
        dfs(s, path, result, prev, start + 1);
        // 如果[prev, start-1] 是回文，则可以断开，也可以不断开（上一行已经做了）
        if (isPalindrome(s, prev, start - 1)) {
            // 断开
            path.push_back(s.substr(prev, start - prev));
            dfs(s, path, result, start, start + 1);
            path.pop_back();
        }
    }

    bool isPalindrome(const string &s, int start, int end) {
        while (start < end && s[start] == s[end]) {
            ++start;
            --end;
        }
        return start >= end;
    }
};

深搜 2 @

// 时间复杂度 O(2^n)，空间复杂度 O(n)
class Solution {
public:
    vector<vector<string>> partition(string s) {
        vector<vector<string>> result;
        vector<string> path;  // 一个partition方案
        dfs(s, path, result, 0, 1);
        return result;
    }

    // prev 表示前一个隔板, start 表示当前隔板
    void dfs(string &s, vector<string>& path,
            vector<vector<string>> &result, size_t prev, size_t start) {
        if (start == s.size()) { // 最后一个隔板
            if (isPalindrome(s, prev, start - 1)) { // 必须使用
                path.push_back(s.substr(prev, start - prev));
                result.push_back(path);
                path.pop_back();
            }
            return;
        }
        // 不断开
        dfs(s, path, result, prev, start + 1);
        // 如果[prev, start-1] 是回文，则可以断开，也可以不断开（上一行已经做了）
        if (isPalindrome(s, prev, start - 1)) {
            // 断开
            path.push_back(s.substr(prev, start - prev));
            dfs(s, path, result, start, start + 1);
            path.pop_back();
        }
    }

    bool isPalindrome(const string &s, int start, int end) {
        while (start < end && s[start] == s[end]) {
            ++start;
            --end;
        }
        return start >= end;
    }
};

动归 @

// 动规，时间复杂度 O(n^2)，空间复杂度 O(1)
class Solution {
public:
    vector<vector<string> > partition(string s) {
        const int n = s.size();
        bool p[n][n]; // whether s[i,j] is palindrome
        fill_n(&p[0][0], n * n, false);
        for (int i = n - 1; i >= 0; --i)
            for (int j = i; j < n; ++j)
                p[i][j] = s[i] == s[j] && ((j - i < 2) || p[i + 1][j - 1]);

        vector<vector<string> > sub_palins[n]; // sub palindromes of s[0,i]
        for (int i = n - 1; i >= 0; --i) {
            for (int j = i; j < n; ++j)
                if (p[i][j]) {
                    const string palindrome = s.substr(i, j - i + 1);
                    if (j + 1 < n) {
                        for (auto v : sub_palins[j + 1]) {
                            v.insert(v.begin(), palindrome);
                            sub_palins[i].push_back(v);
                        }
                    } else {
                        sub_palins[i].push_back(vector<string> { palindrome });
                    }
                }
        }
        return sub_palins[0];
    }
};

动归 @

// Palindrome Partitioning
#define ROF(i, a, b) for (int i = (b); --i >= (a); )
#define FOR(i, a, b) for (int i = (a); i < (b); i++)
#define REP(i, n) for (int i = 0; i < (n); i++)

class Solution {
private:
    vector<vector<bool>> f;
    vector<string> rr;
    vector<vector<string>> r;
    void g(string &s, int i) {
        if (i == s.size())
            r.push_back(rr);
        else
            REP(j, s.size())
                if (f[i][j]) {
                    rr.push_back(s.substr(i, j-i+1));
                    g(s, j+1);
                    rr.pop_back();
                }
    }
public:
    vector<vector<string>> partition(string s) {
        int n = s.size();
        f.assign(n, vector<bool>(n));
        ROF(i, 0, n) {
            f[i][i] = true;
            if (i+1 < n && s[i] == s[i+1])
                f[i][i+1] = true;
            FOR(j, i+2, n)
                f[i][j] = f[i+1][j-1] && s[i] == s[j];
        }
        r.clear();
        g(s, 0);
        return r;
    }
};

refs and see also

TODO @
- 单序列动态规划（下） Sequnece DP
- 双序列动态规划 Two Sequences DP @
  
  state: f[i][j] 代表了第一个 sequence 的前 i 个数字 / 字符, 配上第二个 sequence 的前 j 个…
  
  function: f[i][j] = 研究第 i 个和第 j 个的匹配关系
  
  initialize: f[i] 和 f[i]
  
  answer: f[n][m]
  
  n = s1.length()
  
  m = s2.length()
- problems @
  
  求 Max, Longest Common Subsequence 参考程序 Java/C++/Python @
  
  http://www.lintcode.com/problem/longest-common-substring/
  
  state: f[i][j] 表示前 i 个字符配上前 j 个字符的 LCS 的长度
  
  function:
  
  f[i][j]` = MAX(f[i-1][j], f[i][j-1], f[i-1][j-1] + 1) // A[i - 1] == B[j - 1] = MAX(f[i-1][j], f[i][j-1]) // A[i - 1] != B[j - 1]
  
  intialize: f[i] = 0 f[j] = 0
  
  answer: f[n][m]
  
  求 Min, Edit Distance 参考程序 Java/C++/Python
  
  求方案总数, Distinct Subsequences 参考程序 Java/C++/Python @
  
  state: f[i][j] 表示 S 的前 i 个字符中选取 T 的前 j 个字符, 有多少种方案
  
  function: f[i][j] = f[i - 1][j] + f[i - 1][j - 1] // S[i-1] == T[j-1] = f[i - 1][j] // S[i-1] != T[j-1]
  
  initialize: f[i] = 1, f[j] = 0 (j > 0)
  
  answer: f[n][m] (n = sizeof(S), m = sizeof(T))
  
  求是否可行, Interleaving String 参考程序 Java/C++/Python
  
  什么情况下可能使用/不用动态规划?
  
  最大值最小值 / 是否可行 / 方案总数
  
  求所有方案 / 集合而不是序列 / 指数级到多项式
  
  解决动态规划问题的四点要素
  
  状态, 方程, 初始化, 答案
  
  三种面试常见的动态规划类别及状态特点
  
  坐标, 单序列, 双序列
  
  两招独孤九剑
  
  二维 DP 需要初始化第 0 行和第 0 列
  
  n 个字符的字符串要开 n+1 个位置的数组
  
  其他类型的动态规划(算法强化班) @
  
  背包类:
  
  http://www.lintcode.com/problem/backpack/
  
  http://www.lintcode.com/problem/backpack-ii/
  
  http://www.lintcode.com/problem/minimum-adjustment-cost/
  
  http://www.lintcode.com/problem/k-sum/
  
  区间类:
  
  http://www.lintcode.com/problem/coins-in-a-line-iii/
  
  http://www.lintcode.com/problem/scramble-string/
  
  划分类:
  
  http://www.lintcode.com/problem/best-time-to-buy-and-sell-stock-iv/
  
  http://www.lintcode.com/problem/maximum-subarray-iii/

✂️ 2016/08/14 上午 9:30:00 5. 动态规划 Dynamic Programming II @

Theories @

如果一个问题具有以下两个要素：

最优子结构 (optimal substructure)
(无后效性)
重叠子问题 (overlapping subproblem), 该性质并不是动态规划适用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势

则可以用动态规划求最优解。

动态规划分为 4 个步骤：

描述最优解的结构。即抽象出一个状态来表示最优解。
递归的定义最优解的值。找出状态转移方程，然后递归的定义
计算最优解的值。典型的做法是自底向上 (bottom-up, iteration)，当然也可以自顶向下 (top-down, memoization)。
根据计算过程中得到的信息，构造出最优解。如果我们只需要最优解的值，不需要最优解本身，则可以忽略第 4 步。当执行第 4 步时，我们需要在第 3 步的过程中维护一些额外的信息，以便我们能方便的构造出最优解。

在第 1 步中，我们需要抽象出一个“状态”，在第 2 步中，我们要找出“状态转移方程”，然后才能递归的定义最优解的值。第 3 步和第 4 步就是写代码实现了。

写代码实现时有两种方式，“递归 (recursive)+ 自顶向下 (top-down)+ 表格”和“自底向上 (bottom-up) + 表格”。前者属于一种 memoization （翻译为备忘录法），后者才是正宗的动规。

动规用表格将各个子问题的最优解存起来，避免重复计算，是一种空间换时间。

动规与贪心

相同点：最优子结构。
不同点：
- 1、动规的子问题是重叠的，而贪心的子问题是不重叠的 (disjoint subproblems)；
- 2、动规不具有贪心选择性质；
- 3、贪心的前进路线是一条线，而动规是一个 DAG。

分治和贪心的相同点：disjoint subproblems。

动规和备忘录法的区别

动规 (dynamic programming) 一定是自底向上的，备忘录法 (memoization) 一定是自顶向下的。
动规不是 lazy 的， memoization 是 lazy 的，是按需 (on-demand) 计算的。所以，如果所有的子问题至少会碰到一次，则动规有优势；如果有些子问题在搜索过程中不会被碰到（即有剪枝），则 memorization 有优势。更详细的解释请参考 StackOverflow 上的这个帖子 http://t.cn/z80ZS6B。
备忘录法可以实现跟动规类似的功能，但它不是动规。两者的方向是反的，一个是自顶向下，一个自底向上，我们应该区分开这两个概念。本书后面提到的动规，都是指自底向上的动规。

longest common subsequence @

一个序列的子序列 (subsequence) 是指在该序列中删去若干（可以为 0 个）元素后得到的序列。准确的说，若给定序列 X = (x₁, x₂, …, x_m)，则另一个序列 Z = (z₁, z₂, …, z_k)，是 X 的子序列是指存在一个严格递增下标序列 (i₁, i₂, …, i_k) 使得对于所有 j=1, 2, …, k 有 z_j=x_{i_j}。例如，序列 Z = (B, C, D, B) 是序列 X = (A, B, C, B, D, A, B) 的子序列，相应的递增下标序列为 (1, 2, 4, 6)。

给定两个序列 X 和 Y，求 X 和 Y 的最长公共子序列 (longest common subsequence)。

输入

    输入包括多组测试数据，每组数据占一行，包含两个字符串（字符
    串长度不超过 200），代表两个序列。两个字符串之间由若干个空
    格隔开。

    abcfbc abfcab
    programming contest
    abcd mnp
    nicenice nice

输出

    对每组测试数据，输出最大公共子序列的长度，每组一行。

    4   "abcb"
    2   "on"
    0   ""
    4   "nice"

最长公共子序列问题具有最优子结构性质。

if X[m] & Y[n] ---> Z[k], and

a)      x[m] == y[n], then
                                z[k] = x[m] = y[n], X[m-1] & Y[n-1] ---> Z[k-1]
b)      x[m] != y[n], and
    b1. z[k] != x[m], then
                                X[m-1] & Y[n] ---> Z[k]
    b2. z[k] != y[m], then
                                X[m] & Y[n-1] ---> Z[k]

设状态为 d[i][j]，表示序列 X_i 和 Y_j 的最长公共子序列的长度。由最优子结构可得状态转移方程如下：

                0                               i=0, or j=0
d[i][j]=        d[i-1][j-1] + 1                 i,j>0, x_i == y_i
                max{ d[i][j-1], d[i-1][j] }     i,j>0, x_i != y_i

如果要打印出最长公共子序列，需要另设一个数组 p，p[i][j] 记录 d[i][j] 是由哪个子问题得到的。

#include <cstdio>
#include <cstring>

#define MAX 201                         // 字符串最大长度为200

char x[MAX], y[MAX];
int d[MAX][MAX];                        // d[i][j] 表示序列 Xi 和 Yj 的最长公共子序列的长度

void lcs( const char *x, const int m, const char *y, const int n ) {
    for( int i = 0; i <= m; ++i ) { d[i][0] = 0; }                          // 边界初始化
    for( int j = 0; j <= n; ++j ) { d[0][j] = 0; }
    for( int i = 1; i <= m; ++i ) {
        for( int j = 1; j <= n; ++j ) {
            if( x[i-1] == y[j-1] ) {
                d[i][j] = d[i-1][j-1] + 1;
            } else {
                d[i][j] = d[i-1][j] > d[i][j-1] ? d[i-1][j] : d[i][j-1];    // choose the bigger one
            }
        }
    }
}

void lcs_extend(const char *x, const int m, const char *y, const int n);
void lcs_print(const char *x, const int m, const char *y, const int n);

int main() {
    while ( 2 == scanf ("%s%s", x, y) ) {
        const int lx = strlen(x);
        const int ly = strlen(y);
        lcs(x, lx, y, ly);
        printf ("%d\t", d[lx][ly] );
        {
            lcs_extend(x, lx, y, ly);
            printf("\"");
            lcs_print(x, lx, y, ly);
            printf("\"\n");
        }
    }
    return 0;
}

int p[MAX][MAX];  // p[i][j] 记录 d[i][j] 是由哪个子问题得到的

void lcs_extend( const char *x, const int m, const char *y, const int n ) {
    memset( p, 0, sizeof(p) );                      // sizeof(p) == MAX*MAX*sizeof(int)
    for( int i = 0; i <= m; ++i ) { d[i][0] = 0; }  // 边界初始化
    for( int j = 0; j <= n; ++j ) { d[0][j] = 0; }
    for( int i = 1; i <= m; ++i ) {
        for( int j = 1; j <= n; ++j ) {
            if (x[i-1] == y[j-1]) {
                d[i][j] = d[i-1][j-1] + 1;
                p[i][j] = 1;
            } else {
                if (d[i-1][j] >= d[i][j-1]) {
                    d[i][j] = d[i-1][j];
                    p[i][j] = 2;
                } else {
                    d[i][j] = d[i][j-1];
                    p[i][j] = 3;
                }
            }
        }
    }
}

void lcs_print( const char *x, const int m, const char *y, const int n ) {
    if ( !m || !n ) { return; }
    if (p[m][n] == 1) {
        lcs_print(x, m - 1, y, n - 1);
        printf("%c", x[m - 1]);
    } else if (p[m][n] == 2) {
        lcs_print(x, m - 1, y, n);
    } else {
        lcs_print(x, m, y, n - 1);
    }
}

maximum continuous subsequence sum @

Maximum Subarray (dup)

take a peak

f[j] = max( f[j-1]+S[j], S[j] ), j = 2..n, f = S
target = max{ f[j] }, j = 1..n

代码：

// Time: O(n), Space: O(1)
int maxSubArray( vector<int> &nums ) {
    int result = INT_MIN, f = 0;
    for( int i = 0; i < nums.size(); ++i ) {
        f = max( f+nums[i], nums[i] );
        result = max( f, result );
    }
    return result;
}

最大 M 子段和, maximum m segments sum @

给定一个整数序列 S₁, S₂, …, S_n (1 <= n <= 1,000,000, -32768 <= S_i <= 32768)，定义函数 sum(i,j)= S_i + … + S_j (1 <= i <= j <= n)。

现给定一个正整数 m，找出 m 对 i 和 j，使得 sum(i₁,j₁) + sum(i₂,j₂) + … + sum(i_m,j_m) 最大。这就是 最大 M 子段和 (maximum m segments sum)。

input:

    每个测试用例由两个正整数m和n开头，接着是n个整数。

    1   3       1   2   3
    2   6      -1   4  -2   3  -2   3

output:

    每行输出一个最大和。

    6
    8

分析

设状态为 d[i,j]，表示前 j 项分为 i 段的最大和，且第 i 段必须包含 S[j]，则状态转移方程如下：

d[i,j] = max {
                    d[i,j-1] + S[j],                # S[j] 包含在第 i 段之中，d[i,j-1]+S[j]。
                    max{    d[i-1,t] + S[j] }       # S[j] 独立划分成为一段
             },                                     i <= j <= n, i-1 <= t < j
target = max {      d[m,j]                  },      m <= j <= n

观察上述两种情况可知 d[i,j] 的值只和 d[i,j-1] 和 d[i-1,t] 这两个值相关，因此不需要二维数组，可以用滚动数组，只需要两个一维数组，用 d[j] 表示现阶段的最大值，即 d[i,j-1] + S[j]，用 prev[j] 表示上一阶段的最大值，即 max{ d[i-1,t] + S[j] }。

TODO.

#include <stdio.h>
#include <stdlib.h>
#include <limits.h>

// @brief 最大m段子序列和
// @param[in] S 数组
// @param[in] n 数组长度
// @param[in] m m段
// @return 最大m段子序列和
int mmss(int S[], int n, int m) {
    int max_sum, i, j;

    /* d[i]表示现阶段最大值，prev[i]表示上阶段最大值 */
    /* d[0], prev[0] 未使用 */
    int *d = (int*) calloc(n + 1, sizeof(int));
    int *prev = (int*) calloc(n + 1, sizeof(int));
    S--;  // 因为 j是从1开始，而S从0开始，这里要减一

    for (i = 1; i <= m; ++i) {
        max_sum = INT_MIN;
        for (j = i; j <= n; ++j) {
            // 状态转移方程
            if (d[j - 1] < prev[j - 1])
                d[j] = prev[j - 1] + S[j];
            else
                d[j] = d[j - 1] + S[j];

            prev[j - 1] = max_sum;  // 存放上阶段最大值
            if (max_sum < d[j])
                max_sum = d[j];  // 更新 max_sum
        }
        prev[j - 1] = max_sum;
    }

    free(d);
    free(prev);
    return max_sum;
}

int main() {
    int n, m, i, *S;
    while (scanf("%d%d", &m, &n) == 2) {
        S = (int*) malloc(sizeof(int) * n);
        for (i = 0; i < n; ++i)
            scanf("%d", &S[i]);
        printf("%d\n", mmss(S, n, m));
        free(S);
    }
    return 0;
}

背包问题 @

背包问题 (Knapsack problem)

有很多种版本，常见的是以下三种：

0-1 背包问题 (0-1 knapsack problem)：每种物品只有一个
完全背包问题 (UKP, unbounded knapsack problem)：每种物品都有无限个可用
多重背包问题 (BKP, bounded knapsack problem)：第 i 种物品有 c[i] 个可用

背包问题是一种“多阶段决策问题”。

这部分来自崔添翼：tianyicui/pack: 背包问题九讲。

0-1背包问题 @

有 N 件物品和一个容量为 V 的背包。放入第 i 件物品耗费的费用是 C_i，得到的价值是 W_i。求解将哪些物品装入背包可使价值总和最大。

input:

    第 1 行包含一个整数 T，表示有 T 组测试用例。
    每组测试用例有 3 行，第 1 行包含两个整数 N, W (N <= 1000 , W <= 1000)
    分别表示物品的种数和背包的容量，第 2 行包含 N 个整
    数表示每种物品的价值，第 3 行包含 N 个整数表示每种
    物品的重量。

    1
    5 10
    1 2 3 4 5
    5 4 3 2 1

output:

    每行一个整数，表示价值总和的最大值。

    14

这是最基础的背包问题，特点是：每种物品仅有一件，可以选择放或不放。

用子问题定义状态：即 F[i,v] 表示前 i 件物品放入一个容量为 v 的背包可以获得的最大价值。则其状态转移方程便是：

                            不放                            放
F[i,v] = max{           F[i−1, v],                  F[i−1, v−C_i] + W_i         }

动规过程的伪代码如下：

f[0..N][0..W] = 0
for i=1..N
    for j=0..W
        f[i][j] = max{      f[i-1][j],      f[i-1][j-w[i]]+v[i]     };

内循环从右向左也可以：

f[0..N][0..W] = 0
for i=1..N
    for j=W..0
        f[i][j] = max{      f[i-1][j],      f[i-1][j-w[i]]+v[i]     };

内循环从右向左时，可以把二维数组优化成一维数组。伪代码如下：

for i=1..N
    for j=W..0
        d[j]    = max{           d[j],           d[j-w[i]]+v[i]     };
     // f[i][j] = max{      f[i-1][j],      f[i-1][j-w[i]]+v[i]     };
     //                                             ^
     //                                             |
     //                                             +-- still valid, so we can
     //                                                 iterate from right to left

为什么呢？

当内循环是逆序时，且动规是用自底向上方式实现时，就可以保证同一行可以从右向左更新。

设一维数组为 d（又称为滚动数组，在更新 d[j] 之前，d[j] 里保存的 f[i-1][j]，更新之后，d[j] 里保存的是 f[i][j] )。

事实上，使用一维数组解 0-1 背包问题的程序在后面会被多次用到，所以这里抽象出一个处理单个物品的函数，以后的代码中直接调用不加说明。

def ZeroOneKnapsack(d[], i)
    for j = W..w[i]
        d[j] = max( d[j], d[j-w[i]] + v[i] )

有了这个函数以后，0-1 背包问题的伪代码就可以这样写：

d[0..W] = 0
for i = 1..N
    ZeroOneKnapsack(d[], i)

版本1，自底向上 @

#include <stdio.h>
#include <string.h>

#define MAXN 1000
#define MAXW 1000

int N, W;
int w[MAXN+1], v[MAXN+1];               // 0 没有用
int f[MAXN + 1][MAXW + 1];

void dp() {
    int i, j;
    memset(f, 0, sizeof(f));            // 背包不一定要装满
    for( int i = 1; i <= N; ++i ) {
        // for( int j = W; j >= 0; --j ) {
        for( int j = 0; j <= W; ++j ) {
            f[i][j] = f[i-1][j];
            if(j >= w[i]) {
                int sum = f[i-1][j-w[i]] + v[i];    // when i = 1, init f[0][i] to v[i]
                if(sum > f[i][j]) f[i][j] = sum;
            }
        }
    }
}

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        scanf("%d %d", &N, &W);
        for( int i = 1; i <= N; ++i ) scanf("%d", &v[i]);
        for( int i = 1; i <= N; ++i ) scanf("%d", &w[i]);
        dp();
        printf("%d\n", f[N][W]);
    }
    return 0;
}

版本2，自底向上，滚动数组 @

#include <stdio.h>
#include <string.h>

#define MAXN 1000
#define MAXW 1000

int N, W;
int w[MAXN], v[MAXN];

int d[MAXW + 1];

// put ith object
void zero_one_knapsack(int d[], const int i) {
    for( int j = W; j >= w[i]; --j ) {
        int sum = d[j - w[i]] + v[i];
        if(sum > d[j]) { d[j] = sum; }
    }
}

void dp() {
    memset(d, 0, sizeof(d));
    for( int i = 0; i < N; ++i ) {
        zero_one_knapsack(d, i);
    }
}

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        scanf("%d %d", &N, &W);
        for( int i = 1; i <= N; ++i ) scanf("%d", &v[i]);
        for( int i = 1; i <= N; ++i ) scanf("%d", &w[i]);

        dp();
        printf("%d\n", d[W]);
    }
    return 0;
}

WORKS??

9???

完全背包问题 @

给你一个储钱罐 (piggy bank)，往里面存硬币。存入的过程是不可逆的，要想把钱拿出来只能摔碎储钱罐。因此，你想知道里面是否有足够多的钱，把它摔碎是值得的。

你可以通过储钱罐的重量来推测里面至少有多少钱。已知储钱罐空的时候的重量和装了硬币后的重量，还有每种硬币的重量和面值，每种硬币的数量不限。求在最坏情况下，储钱罐里最少有多少钱。

输入

    第 1 行包含一个整数 T，表示有 T 组测试用例。每组测
    试用例，第一行是两个整数 E 和 F，分别表示空储钱罐的
    重量和装了硬币后的重量，以克 (gram) 为单位，储钱罐
    的重量不会超过 10kg，即 1 <= E <= F <= 10000。第二
    行是一个整数N (1 <= N <= 500)，表示硬币的种类数目。
    接下来是 N 行，每行包含两个整数 v 和 w
    (1 <= v <= 50000, 1 <= w <= 10000)，分别表示硬币的面值和重量。

    3
    10 110
    2
    1 1
    30 50
    10 110
    2
    1 1
    50 30
    1 6
    2
    10 3
    20 4

输出

    每个案例打印一行。内容是 "The minimum amount of money in the piggy-bank is X."，
    其中 X 表示储钱罐里最少有多少钱。如果不能精确地达到给定的重量，则打印
    "This is impossible."。

    The minimum amount of money in the piggy-bank is 60.
    The minimum amount of money in the piggy-bank is 100.
    This is impossible.

每种物品有无限个可用，这是完全背包问题。

本题没有给出储钱罐的容量，但每个案例给出了，初始为空时的重量 E 和装了硬币后的重量 F，因此可以把储钱罐看作一个容量为 F-E 的背包，背包必须要装满。

这个问题非常类似于 0-1 背包问题，所不同的是每种物品有无限个。也就是从每种物品的角度考虑，与它相关的策略已并非取或不取两种，而是取 0 个、取 1 个、取 2 个……直至取 W/w[i] 个。

一种好想好写的基本方法是转化为 0-1 背包问题：把第 i 种物品换成 W/w[i] 个 0-1 背包问题中的物品，则得到了物品数为 sum(W/W[i]) 的 0-1 背包问题。时间复杂度是 O(W*sum(W/W[i]))

按照该思路，状态转移方程为：

f[i][j] = max {
                        f[i-1][j-k*w[i]] + k*v[i]
},                                                                  0 <= k*w[i] <= j
                                                                    0 <= k      <= j/w[i]

伪代码如下：

for i = 1..N
    for j = W..w[i]
        for k = 1..j/w[i]
            d[j] = max{ d[j], d[j-k*w[i]] + k*v[i] };

也可以写成：

for i = 1..N
    for k = 1..W/w[i]
        ZeroOneKnapsack(d[], w, v)

“拆分物品”还有更高效的拆分方法： @

把第 i 种物品拆分成重量为 2^k × w[i]、价值为 2^k × v[i] 的若干物品，其中 k 取所有满足 2^k × w[i] <= W 的非负整数。这是二进制的思想，因为闭区间 [1, W/w[i]] 中的任何整数都可以表示为 1, 2, 4, …, 2^k 中若干个的和。

这样处理单个物品的复杂度由 O(W/w[i]) 降到了 O(lg(W/w[i]))，伪代码如下：

def UnboundedKnapsack(d[], i)
    k=1
    while k*w[i] <= W
        ZeroOneKnapsack(d[], k*w[i], k*v[i])
        k=2*k

还存在更优化的算法，复杂度为 O(NW)，伪代码如下：

for i = 1..N
    for j = 0..W
        d[j] = max{ d[j], d[j-w[i]] + v[i]  };

与 0-1 背包问题相比，仅有一行代码不同，这里内循环是顺序的，而 0-1 背包是逆序的（在使用滚动数组的情况下）。

为什么这个算法可行呢？首先想想为什么 0-1 背包中内循环要逆序，逆序是为了保证每个物品只选一次，保证在“选择第 i 件物品”时，依赖的是一个没有选择第 i 件物品的子结果 f[i-1][j-w[i]]。而现在完全背包的特点却是每种物品可选无限个，没有了每个物品只选一次的限制，所以就可以并且必须采用 j 递增的顺序循环。

根据上面的伪代码，状态转移方程也可以写成这种形式：

f[i][j] = max {
                        f[i-1][j],
                        f[i][j-w[i]] + v[i]
}

抽象出处理单个物品的函数：

def UnboundedKnapsack(d[], i)
    for j = w[i]..W
        d[j] = max(d[j], d[j-w[i]] + v[i])

code

#include <stdio.h>

#define MAXN 500
#define MAXW 10000

const int INF = 0x0FFFFFFF;                     // 无效值，不要用 0x7FFFFFFF，执行加运算后会变成负数

int N, W;
int w[MAXN], v[MAXN];
int d[MAXW + 1];

// @brief 完全背包问题中，处理单个物品.
// @param[in] d 滚动数组
// @param[in] i 该物品的下标
// @return 无
void unbounded_knapsack(int d[], const int i) {
    for( int j = w[i]; j <= W; ++j ) {
        int sum = d[j - w[i]] + v[i];
        if( sum < d[j] ) { d[j] = sum; }        // min!
                                                // "求在最坏情况下，储钱罐里最少有多少钱。"
    }
}
// c，物品的系数
void zero_one_knapsack(int d[], const int i, const int c) {
    const int neww = c * w[i];
    const int newv = c * v[i];
    for( int j = W; j >= neww; --j) {
        const int tmp = d[j - neww] + newv;
        if(tmp < d[j]) d[j] = tmp;
    }
}

void unbounded_knapsack1(int d[], const int i) {
    int k = 1;
    while(k * w[i] <= W) {
        zero_one_knapsack(d, i, k);
        k *= 2;
    }
}

void dp() {
    for( int i = 0; i <= W; ++i ) { d[i] = INF; }   // 背包要装满
    d[0] = 0;
    for( int i = 0; i <  N; ++i ) { unbounded_knapsack(d, i); }
}

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        int E, F;
        scanf("%d %d", &E, &F);
        W = F - E;
        scanf("%d", &N);
        for( int i = 0; i < N; ++i ) {
            scanf("%d %d", &v[i], &w[i]);
        }
        dp();
        if(d[W] == INF) {
            printf("This is impossible.\n");
        } else {
            printf("The minimum amount of money in the piggy-bank is %d.\n",
                    d[W]);
        }
    }
    return 0;
}

// 将第 i 种物品取 0 个，1 个，...，W/w[i] 个，该版本不能 AC，会 TLE
void unbounded_knapsack2(int d[], const int w, const int v) {
    int j, k;
    for(j = W; j >= w; --j) {
        const int K = j / w;
        for(k = 1; k <= K; ++k) {
            const int tmp = d[j - k * w] + k * v;
            if(tmp < d[j]) d[j] = tmp; /* 求最小用 <，求最大用 > */
        }
    }
}

// 将第 i 种物品取 0 个，1 个，...，W/w[i] 个，该版本不能 AC，会 TLE
void unbounded_knapsack3(int d[], const int w, const int v) {
    int k;
    const int K = W / w;
    for(k = 0; k < K; ++k){
        zero_one_knapsack(d, w, v);
    }
}

多重背包问题 @

某地发生地震，为了挽救灾区同胞的生命，心系灾区同胞的你准备自己采购一些粮食支援灾区，现在假设你一共有资金 W 元，而市场有 N 种大米，每种大米都是袋装产品，其价格不等，并且只能整袋购买。

请问：你用有限的资金最多能采购多少公斤粮食呢？

输入

    第 1 行包含一个整数 T，表示有 T 组测试用例。
    每组测试用例的第一行是两个整数 W 和 N(1 <= W <= 100, 1 <= N <= 100),
    分别表示经费的金额和大米的种类，然后是 N 行数据，
    每行包含 3 个整数 w，v 和 c (1 <= w <= 20,1 <= v <= 200,1 <= c <= 20)，
    分别表示每袋的价格、每袋的重量以及对应种类大米的袋数。

    1
    8 2
    2 100 4
    4 100 2

输出

    对于每组测试用例，输出能够购买大米的最大重量，你可
    以假设经费买不光所有的大米，并且经费你可以不用完。
    每个实例的输出占一行。

    400

第 i 种物品有 c[i] 个可用，这是多重背包问题。

与完全背包问题类似，也可以用“拆分物品”的思想把本问题转化为 0-1 背包问题：把第 i 种物品换成 c[i] 个 0-1 背包问题中的物品，则得到了物品数为 sum( c[i] ) 的 0-1 背包问题。时间复杂度是 O(W/sum{c[i]})。状态转移方程为：

f[i][j] = max {
                f[i-1][j-k*w[i]] + k*v[i]
},                                                  0 <= k <= c[i], 0 <= k*w[i] <= j
                                                    0 <= k <= min(c[i], j/w[i])

伪代码如下：

for i = 1..N
    for j = W..w[i]
        K = min{j/w[i], c[i]}
        for k = 1..K                                // k = 0, already considered in max( d[j], 'value when choose k' )
            d[j] = max{d[j], d[j-k*w[i]] + k*v[i]};

也可以写成：

for i = 1..N
    for k = 1..c[i]
        ZeroOneKnapsack(d[], i)

拆分物品也可以使用二进制的技巧，把第 i 种物品拆分成若干物品，其中每件物品都有一个系数，这个新物品的重量和价值均是原来的重量和价值乘以这个系数。系数分别为 1, 2, 2², …, 2^k-1, c[i]-(2^k-1)，其中 k 是满足 2^k - 1 < c[i] 的最大整数。例如，某种物品有 13 个，即 c[i]=13，则相应的 k=3，这种物品应该被拆分成系数分别 1, 2, 4 (2²), 6 (13-(2³-1)) 的四个物品。

这样处理单个物品的复杂度由 O(c[i]) 降到了 O(log(c[i]))，伪代码如下：

// c, 物品系数
def ZeroOneKnapsack(d[], i, c)
    for j = W..w[i]
        d[j] = max(d[j], d[j-c*w[i]] + c*v[i])
def BoundedKnapsack(d[], i)
    if c[i]*w[i] >= W
        unbounded_knapsack(d[], i);
        return;

    k = 1;
    while k < c[i]
        zero_one_knapsack(d[], i, k);
        c[i] -= k;
        k *= 2;

    zero_one_knapsack(d[], i, c);

#include <stdio.h>
#include <string.h>

#define MAXN 100
#define MAXW 100

int N, W;
int w[MAXN], v[MAXN], c[MAXN];

int d[MAXW + 1];

// c，物品的系数
void zero_one_knapsack(int d[], const int i, const int c) {
    const int neww = c * w[i];
    const int newv = c * v[i];
    for( int j = W; j >= neww; --j ) {
        const int tmp = d[j - neww] + newv;
        if(tmp > d[j]) d[j] = tmp;
    }
}

void unbounded_knapsack(int d[], const int i) {
    for( int j = w[i]; j <= W; ++j ) {
        const int tmp = d[j - w[i]] + v[i];
        if(tmp > d[j]) d[j] = tmp;
    }
}

// @brief 多重背包问题中，处理单个物品.
// @param[in] d 滚动数组
// @param[in] i 该物品的下标
// @param[in] c 该物品的数量
// @return 无
void bounded_knapsack(int d[], const int i) {
    for( int k = 0; k < c[i]; ++k ) {
        zero_one_knapsack(d, i, 1);
    }
}

// 另一个版本，拆分物品更加优化
void bounded_knapsack1(int d[], const int i) {
    if(c[i] * w[i] >= W) {
        unbounded_knapsack(d, i);
        return;
    }

    int k = 1;
    while(k < c[i]) {
        zero_one_knapsack(d, i, k);
        c[i] -= k;
        k *= 2;
    }
    zero_one_knapsack(d, i, c[i]);
}

void dp() {
    memset(d, 0, sizeof(d));
    for( int i = 0; i < N; ++i ) { bounded_knapsack1(d, i); }
}

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        scanf("%d %d", &W, &N);
        for( int i = 0; i < N; ++i ) { scanf("%d %d %d", &w[i], &v[i], &c[i]); }
        dp();
        printf("%d\n", d[W]);
    }
    return 0;
}

序列型动态规划 @

对于所有动规题目，如果把状态转移图画出来，一定是一个有向无环图 (DAG)。再进一步细分类别，有序列型动态规划，棋盘型动态规划，树型动态规划等等。

最长上升子序列 ♥️ @

当一个序列严格递增时，我们称这个序列是上升的。

对于一个给定的序列 a₁, a₂, …, a_N，我们可以得到一些上升的子序列 a_i1, a_i2, …, a_iK，这里 1 <= i₁ < i₂ < … < i_K <= N。例如，对于序列 (1, 7, 3, 5, 9, 4, 8)，有它的一些上升子序列，如 (1, 7), (3, 4, 8) 等等，这些子序列中最长的长度是 4，比如子序列 (1, 3, 5, 8)。

对于给定的序列，求最长上升子序列 (longest increasing subsequence) 的长度。

输入

    第一行是序列的长度 N (1 <= N <= 1000)。
    第二行给出序列中的 N 个整数，这些整数的取值范围都在0 到 10000。

    7
    1 7 3 5 9 4 8

输出

    最长上升子序列的长度。

    4

设状态为 d[j]，表示以 a_j 为终点的最长上升子序列的长度。状态转移方程如下；

d[j]= max {
                    1,                          j=1
                    max{ d[i] } + 1,            1 < i < j, a_i < a_j
}

#include<stdio.h>

#define MAXN 1001                           // a[0]未用
int N, a[MAXN], d[MAXN];

void dp() {
    d[1] = 1;
    for( int j = 2; j <= N; ++j ) {         // 每次求以 aj 为终点的最长上升子序列的长度
        int max = 0;                        // 记录 aj 左边的上升子序列的最大长度
        for ( int i = 1; i < j; ++i )  {
            if (a[i] <a[j] && max < d[i]) {
                max = d[i];
            }
        }
        d[j] = max + 1;
    }
}

int main() {
    scanf( "%d",&N );
    for( int i = 1; i <= N; ++i ) {
        scanf( "%d",&a[i] );
    }

    dp();

    int max = 0;
    for( int i = 1; i <= N; ++i ) {
        if( d[i] > max ) {
            max = d[i];
        }
    }
    printf( "%d\n", max );
    return 0;
}

嵌套矩形 @

有 n 个矩形，每个矩形可以用 a,b 来描述，表示长和宽。矩形 X(a,b) 可以嵌套在矩形 Y(c,d) 中当且仅当 a<c,b<d 或者 b<c,a<d（相当于旋转 X90 度）。例如 (1,5) 可以嵌套在 (6,2) 内，但不能嵌套在 (3,4) 中。你的任务是选出尽可能多的矩形排成一行，使得除最后一个外，每一个矩形都可以嵌套在下一个矩形内。

输入

    第一行是一个正整数 N(0<N<10)，表示测试数据组数，
    每组测试数据的第一行是一个正正数 n，表示该组测试数
    据中含有矩形的个数 (n<=1000), 随后的 n 行，每行有两
    个数 a, b (0<a,b<100)，表示矩形的长和宽

    1
    10
    1 2
    2 4
    5 8
    6 10
    7 9
    3 1
    5 8
    12 10
    9 7
    2 2

输出

    每组测试数据都输出一个数，表示最多符合条件的矩形数目，每组输出占一行

    5

本题实质上是求 DAG 中不固定起点的最长路径。

设 d[i] 表示从结点 i 出发的最长长度，状态转移方程如下：

d[i] = max {
                        d[j]+1,                     (i,j) ~ E
}

其中，E 为边的集合。最终答案是 d[i] 中的最大值。

#include <stdio.h>
#include <string.h>

#define MAXN 1000                           // 矩形最大个数

int n;                                      // 矩形个数
int G[MAXN][MAXN];                          // 矩形包含关系
int d[MAXN];                                // 表格

// @brief 备忘录法.
// @param[in] i 起点
// @return 以 i 为起点，能达到的最长路径
int dp(const int i) {
    int *ans= &d[i];
    if( *ans > 0 ) { return *ans; }

    *ans = 1;
    for( int j = 0; j < n; ++j ) {
        if(G[i][j]) {
            int next = dp(j) + 1;
            if( *ans < next ) {
                *ans = next;
            }
        }
    }
    return *ans;
}

// @brief 按字典序打印路径.
// 如果多个 d[i] 相等，选择最小的 i。
// @param[in] i 起点
void print_path(const int i) {
    printf("%d ", i);
    for( int j = 0; j < n; ++j ) {
        if(G[i][j] && d[i] == d[j] + 1) {
            print_path(j);
            break;
        }
    }
}

int main() {
    int N, i, j;
    int max, maxi;
    int a[MAXN],b[MAXN];

    scanf("%d", &N);
    while(N--) {
        memset(G, 0, sizeof(G));
        memset(d, 0, sizeof(d));

        scanf("%d", &n);
        for(i = 0; i < n; i++) scanf("%d%d", &a[i], &b[i]);

        for(i = 0; i < n; i++)
            for(j = 0; j < n; j++)
                if((a[i] > a[j] && b[i] > b[j]) ||
                    (a[i] > b[j] && b[i] > a[j])) G[i][j] = 1;

        max = 0;
        maxi = -1;
        for(i = 0; i < n; i++) if(dp(i) > max) {
            max = dp(i);
            maxi = i;
        }
        printf("%d\n", max);
        // print_path(maxi);
    }
    return 0;
}

线段覆盖 2 @

数轴上有 n (n <= 1000) 条线段，线段的两端都是整数坐标，坐标范围在 0 ~ 1000000，每条线段有一个价值，请从 n 条线段中挑出若干条线段，使得这些线段两两不覆盖（端点可以重合）且线段价值之和最大。

输入

    第一行一个整数 n，表示有多少条线段。

    接下来 n 行每行三个整数, a_i,b_i,c_i，分别代表第 i
    条线段的左端点 a_i，右端点 b_i（保证左端点 < 右端点）
    和价值 c_i。

    3
    1 2 1
    2 3 2
    1 3 4

输出

    输出能够获得的最大价值

    4

先将线段排序。按照右端点从小到大排序。原因是循环结构中是 i 从 1 到 n, i 比较小的时候尽可能选右端点比较小的，这样才可以为后面的线段留下更大的空间。

设状态为 f[i]，表示前 i 条线段时，选上第 i 条线段，能获得的最大价值。状态转移方程如下：

f[i] = max {
                    max{ f[j] } + c[i],         2 <= i <= n, 1 <= j <= i-1, and b[j] <= a[i]
}

b[j] <= a[i] 表示 j 的右端点在 i 的左端点左边，即不重合。

输出 f[i] 数组中的最大值。

// http://www.wikioi.com/problem/3027
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>

#define MAXN 1000

typedef struct line_t {
    int a, b, c;
} line_t;

int line_cmp( const void *a, const void *b ) {
    line_t *la = (line_t*)a;
    line_t *lb = (line_t*)b;
    return la->b - lb->b;
}

int n;
line_t line[MAXN];
int f[MAXN];

void dp() {
    int i, j;
    qsort(line, n, sizeof(line_t), line_cmp);
    f[0] = line[0].c;

    for (i = 1; i < n; i++) {
        int max = 0;
        for (j = 0; j < i; j++) {
            if (line[j].b <= line[i].a) max = max > f[j] ? max : f[j];
        }
        f[i] = max + line[i].c;
    }
}

static int max_element(const int a[], int begin, int end) {
    int i;
    int max_value = INT_MIN;
    int max_pos = -1;
    for (i = begin; i < end; i++) {
        if (max_value < a[i]) {
            max_value = a[i];
            max_pos = i;
        }
    }
    return max_pos;
}


int main() {
    int i;
    scanf("%d", &n);
    for (i = 0; i < n; i++) scanf("%d%d%d", &line[i].a, &line[i].b, &line[i].c);
    dp();
    printf("%d\n", f[max_element(f, 0, n)]);
    return 0;
}

硬币问题 @

有 n 种硬币，面值为别为 v₁, v₂, v₃, …, v_n，每种都有无限多。给定非负整数 S，可以选取多少个硬币，使得面值和恰好为 S？输出硬币数目的最小值和最大值。 1 <= n <= 100, 1 <= S <= 10000, 1 <= v_i <= S。

输入

    第 1 行 n，第 2 行 S，第 3 到 n+2 行为 n 种不同的面值。

    3
    6
    1
    2
    3

输出

    第 1 行为最小值，
    第 2 行为最大值。

    2
    6

本题实质上是求 DAG 中固定终点的最长路径和最短路径。

把每种面值看作一个点，表示“还需要凑足的面值”，则初始状态为 S，目标状态为 0。若当前状态为 i，每使用一个硬币 j，状态便转移到 i-v_j。

设状态为 d[i]，表示从节点 i 出发的最长路径长度，则原问题的解是 d[S]。状态转移方程如下：

d[i] = max {
                            d[j] + 1,                   (i,j) ~ E
}

本题还可以看作是完全背包问题: 背包容量为 S，背包必须要装满，物品即硬币，每个硬币的费用为面值 v_i，价值均为 1。求背包中物品的最小价值和最大价值。

版本 1，备忘录法。 @

#include<stdio.h>
#include <string.h>

#define MAXN 100
#define MAXV 10000

/** 硬币面值的种类. */
int n;
/** 要找零的数目. */
int S;
/** 硬币的各种面值. */
int v[MAXN];
/** min[i] 表示面值之和为i的最短路径的长度，max则是最长. */
int min[MAXV + 1], max[MAXV + 1];

/**
 * @brief 最短路径.
 * @param[in] s 面值
 * @return 最短路径长度
 */
int dp1(const int s) { // 最小值
    int i;
    int *ans = &min[s];
    if(*ans != -1) return *ans;
    *ans = 1<<30;
    for(i = 0; i < n; ++i) if(v[i] <= s) {
        const int tmp = dp1(s-v[i])+1;
        *ans = *ans < tmp ? *ans : tmp;
    }
    return *ans;
}

int visited[MAXV + 1];
/**
 * @brief 最长路径.
 * @param[in] s 面值
 * @return 最长路径长度
 */
int dp2(const int s) { //最大值
    int i;
    int *ans = &max[s];

    if(visited[s]) return max[s];
    visited[s] = 1;

    *ans = -1<<30;
    for(i = 0; i < n; ++i) if(v[i] <= s) {
        const int tmp = dp2(s-v[i])+1;
        *ans = *ans > tmp ? *ans : tmp;
    }
    return *ans;
}

void print_path(const int* d, const int s);

int main() {
    int i;
    scanf("%d%d", &n, &S);
    for(i = 0; i < n; ++i) scanf("%d", &v[i]);

    memset(min, -1, sizeof(min));
    min[0] = 0;
    printf("%d\n", dp1(S));
    // print_path(min, S);

    memset(max, -1, sizeof(max));
    memset(visited, 0, sizeof(visited));
    max[0] = 0; visited[0] = 1;
    printf("%d\n", dp2(S));
    // print_path(max, S);

    return 0;
}

/**
 * @brief 打印路径.
 * @param[in] d 上面的 min 或 min
 * @param[in] s 面值之和
 * @return 无
 */
void print_path(const int* d, const int s) {//打印的是边
    int i;
    for(i = 0; i < n; ++i) if(v[i] <= s && d[s-v[i]] + 1 == d[s]) {
        printf("%d ",i);
        print_path(d, s-v[i]);
        break;
    }
    printf("\n");
}

版本2，自底向上。 @

#include<stdio.h>

#define MAXN 100
#define MAXV 10000

int n, S, v[MAXN], min[MAXV + 1], max[MAXV + 1];
int min_path[MAXV], max_path[MAXV];

void dp() {
    int i, j;

    min[0] = max[0] = 0;
    for(i = 1; i <= S; ++i) {
        min[i] = MAXV;
        max[i] = -MAXV;
    }

    for(i = 1; i <= S; ++i) {
        for(j = 0; j < n; ++j) if(v[j] <= i) {
            if(min[i-v[j]] + 1 < min[i]) {
                min[i] = min[i-v[j]] + 1;
                min_path[i] = j;
            }
            if(max[i-v[j]] + 1 > max[i]) {
                max[i] = max[i-v[j]] + 1;
                max_path[i] = j;
            }
        }
    }
}

void print_path(const int *d, int s);

int main() {
    int i;
    scanf("%d%d", &n, &S);
    for(i = 0; i < n; ++i) scanf("%d", &v[i]);

    dp();
    printf("%d\n", min[S]);
    // print_path(min_path, S);
    printf("%d\n", max[S]);
    // print_path(max_path, S);
    return 0;
}

/**
 * @brief 打印路径.
 * @param[in] d 上面的 min_path 或 min_path
 * @param[in] s 面值之和
 * @return 无
 */
void print_path(const int *d, int s) {
    while(s) {
        printf("%d ", d[S]);
        S -= v[d[s]];
    }
    printf("\n");
}

版本 3，当作完全背包问题。 @

#include<stdio.h>

#define MAXN 100
#define MAXV 10000

int n, S, v[MAXN], min[MAXV + 1], max[MAXV + 1];
int min_path[MAXV], max_path[MAXV];

void dp() {
    int i, j;

    min[0] = max[0] = 0;
    for(i = 1; i <= S; ++i) {
        min[i] = MAXV;
        max[i] = -MAXV;
    }

    for(i = 1; i <= S; ++i) {
        for(j = 0; j < n; ++j) if(v[j] <= i) {
            if(min[i-v[j]] + 1 < min[i]) {
                min[i] = min[i-v[j]] + 1;
                min_path[i] = j;
            }
            if(max[i-v[j]] + 1 > max[i]) {
                max[i] = max[i-v[j]] + 1;
                max_path[i] = j;
            }
        }
    }
}

void print_path(const int *d, int s);

int main() {
    int i;
    scanf("%d%d", &n, &S);
    for(i = 0; i < n; ++i) scanf("%d", &v[i]);

    dp();
    printf("%d\n", min[S]);
    // print_path(min_path, S);
    printf("%d\n", max[S]);
    // print_path(max_path, S);
    return 0;
}

/**
 * @brief 打印路径.
 * @param[in] d 上面的 min_path 或 min_path
 * @param[in] s 面值之和
 * @return 无
 */
void print_path(const int *d, int s) {
    while(s) {
        printf("%d ", d[S]);
        S -= v[d[s]];
    }
    printf("\n");
}

区间型动态规划 @

最优矩阵链乘 @

一个 m * n 的矩阵乘以一个 n * p 的矩阵等于一个 m * p 的矩阵，运算量为 m * n * p。

矩阵乘法不满足分配律，但满足结合律，即 A * B * C = (A * B) * C = A * (B * C)。

假设 A、B、C 分别是 2 x 3、3 x 4、4 x 5 的矩阵，则 (A * B) * C 的运算量为 2 x 3 x 4 + 2 x 4 x 5 = 64， A * (B * C) 的运算量为 3 x 4 x 5 + 2 x 3 x 5 = 90，显然第一种运算顺序节省运算量。

给出 N 个矩阵组成的序列，设计一种方法把它们依次乘起来，使得总的运算量尽量小。

输入

    对于每个矩阵序列，只给出它们的维度。每个序列由两个
    部分组成，第一行包含一个整数 N，表示矩阵的个数；接
    下来的 N 行，每行一对整数，分别表示矩阵的行数和列数。
    给出的顺序与矩阵链乘的顺序一致。最后一行 N 为 0，
    表示输入结束。N 不大于 10。

    3
    1 5
    5 20
    20 1
    3
    5 10
    10 20
    20 35
    6
    30 35
    35 15
    15 5
    5 10
    10 20
    20 25
    0

输出

    假设矩阵命名为 A_1,A_2,...,A_N。对每个测试用例输出一
    行，包含一个使用了小括号的表达式，清晰地指出乘法的
    先后顺序。每行输出以"Case x: "为前缀，x 表示测试用例
    编号。如果有多个正确结果，只需要输出其中一个。

    Case 1: (A1 x (A2 x A3))
    Case 2: ((A1 x A2) x A3)
    Case 3: ((A1 x (A2 x A3)) x ((A4 x A5) x A6))

假设第 i 个矩阵 A_i 的维度是 p_i-1 * p_i, i=1..N。

设状态为 d[i][j]，表示子问题 A_i, A_i+1, …, A_j 的最优解，状态转移方程如下：

d[i][j] = min {
                    d[i][k] + d[k+1][j] + p_{i-1} * p_k * p_j
}

#include <stdio.h>
#include <memory.h>
#include <limits.h>

#define INF INT_MAX
#define MAXN 10

int N;  /** 矩阵的个数. */
int p[MAXN + 1];  /** 矩阵Ai的维度是p[i-1]xp[i]. */
int d[MAXN][MAXN];  /** 状态，d[i][j]表示子问题Ai~Aj 的最优解. */
int s[MAXN][MAXN]; /** 子问题Ai~Aj 应该在s[i][j]处断开 */

/**
 * @brief 打印子问题Ai~Aj的解
 * @param[in] i Ai
 * @param[in] j Aj
 * @return 无
 */
void print(const int i, const int j) {
    if (i == j) {
        printf("A%d",i);
    } else {  /* i < j */
        printf("(");
        print(i, s[i][j]);
        printf(" x ");
        print(s[i][j]+1, j);
        printf(")");
    }
}

void dp() {
    int i, j, k, l; /* l表示区间长度 */
    for (i = 1;i <= N; ++i) d[i][i]=0;

    for (l = 2; l <= N; ++l) {
        for (i = 1; i <= N - l + 1; ++i) {
            j = i + l -1;
            d[i][j] = INF;
            for (k = i; k < j; ++k) {
                if (d[i][j] > d[i][k] + d[k+1][j] + p[i-1] * p[k] * p[j]) {
                    d[i][j] = d[i][k] + d[k+1][j] + p[i-1] * p[k] * p[j];
                    s[i][j] = k;
                }
            }
        }
    }
}

int main() {
    int i;
    int cas = 1;
    while (scanf("%d", &N) && N > 0) {
        memset(s, 0, sizeof(s));
        for (i = 0; i < N; ++i)  scanf("%d %d",&p[i],&p[i+1]);

        dp();

        printf("Case %d: ", cas++);
        print(1, N);
        printf("\n");
    }
    return 0;
}

Matrix67 - 十个利用矩阵乘法解决的经典题目，http://www.matrix67.com/blog/archives/276

石子合并 @
在一条直线上摆着 N 堆石子。现要将石子有次序地合并成一堆。规定每次只能选相邻的 2 堆石子合并成新的一堆，并将新的一堆石子数记为该次合并的得分。

试设计一个算法，计算出将 N 堆石子合并成一堆的最小得分。
```
输入

    第一行是一个数 N, 1 <= N <= 40000，表示堆数。

    接下来的 N 行每行一个数，表示该堆的石子数目。

    4
    1
    1
    1
    1

输出

    一个整数，即 N 堆石子合并成一堆的最小得分。

    8
```
这题与前面的矩阵链乘非常相似，只是计算代价的方式不同。设状态为 d(i,j)，表示子问题第 i 堆到第 j 堆石子的最优解，状态转移方程如下：
```
d(i,j) = min {
                    d(i,k) + d(k+1,j) + sum(i,j)
}
```
sum(i,j) 表示从第 i 堆到第 j 堆的石子总数。代码见 https://gist.github.com/soulmachine/6195139

上面的动规算法可以用四边形不等式进行优化，将时间复杂度从 O(N³) 下降到 O(N²)。

无论如何，时间复杂度都是 O(N²)，本题中 N 范围特别大，开不了这么大的二维数组。所以动规算法只能处理小规模的情况。下面介绍第三种解法，Garsia-Wachs 算法

假设我们只对 3 堆石子 a,b,c 进行合并, 先合并哪两堆, 能使得得分最小？有两种方案：
```
score1 = (a+b) + ((a+b)+c)
score2 = (b+c) + ((b+c)+a)
```
假设 score1 <= score2, 可以推导出 a <= c，反过来，只要 a 和 c 的关系确定，合并的顺序也确定。这就是2- 递减性质。

Garsia-Wachs 算法，就是基于这个性质，找出序列中满足 A[i-1] <= A[i+1] 最小的 i，合并 temp = A[i]+A[i-1]，接着往前面找是否有满足 A[j] > temp，把 temp 值插入 A[j] 的后面 (数组的右边)。循环这个过程一直到只剩下一堆石子结束。

例如, 13 9 5 7 8 6 14, 首先，找第一个满足 A[i-1] <= A[i+1] 的三个连续点，本例中就是 5 7 8，5 和 7 合并得到 12，12 不是丢在原来的位置，而是将它插入到第一个比它大的元素的后面，得到 13 12 9 8 6 14

接着来，从左到右搜索三个连续点，找到 8 6 14，合并 8 和 6 的到 14，将 14 插入到适当位置，得到 14 13 12 9 14

找到 12 9 14，合并 12 和 9 得到 21，将 21 插入到适当位置，得到 21 14 13 14

找到 14 13 14，合并 14 和 13 得到 27，将 27 插入到适当位置，得到 27 21 14

因为 27<14，先合并 21 和 14，得到 35，最后合并 27 和 35，得到 62，就是最终答案。

为什么要将 temp 插入 A[j] 的后面, 可以理解为是为了保持 2- 递减性质。从 A[j+1] 到 A[i-2] 看成一个整体 A[mid]，现在 A[j], A[mid], temp(A[i-1]+A[i])，因为 temp < A[j]，因此不管怎样都是 A[mid] 和 temp 先合并, 所以将 temp 值插入 A[j] 的后面不会影响结果。
```
#include <stdio.h>
#define MAXN 55555

int N, A[MAXN];                                         // 堆数，每堆的石头个数
int num, result;                                        // 数组实际长度，结果

void combine(int k) {                                   // 前提 A[k-1] < A[k+1]
    int temp=A[k] + A[k-1];                             // 合并 k-1和k
    result += temp;

    for( int i = k; i < num - 1; ++i ) {                // 紧缩
        A[i] = A[i+1];
    }
    num--;

    int j;
    for( j = k-1; j > 0 && A[j-1] < temp; --j ) {       // 插入temp到合适位置
        A[j] = A[j-1];
    }
    A[j] = temp;
    while( j >= 2 && A[j] >= A[j-2] ) {                 // why?
        int d = num - j;
        combine(j - 1);
        j = num - d;
    }
}

int main() {
    scanf("%d",&N);
    if( !N ) { return 0; }
    for( int i = 0; i < N; ++i ) {
        scanf("%d", &A[i]);
    }

    num=2;
    result=0;
    for( int i = 2; i < N; i++) {
        A[num++] = A[i];
        while(num >= 3 && A[num-3] <= A[num-1]) combine(num-2);
    }
    while(num > 1) combine(num-1);
    printf("%d\n",result);
    return 0;
}
```

矩阵取数游戏 @

帅帅经常跟同学玩一个矩阵取数游戏：对于一个给定的 n*m 的矩阵，矩阵中的每个元素 a_ij 均为非负整数。游戏规则如下：

每次取数时须从每行各取走一个元素，共 n 个，m 次后取完矩阵所有元素；
每次取数时须从每行各取走一个元素，共 n 个，m 次后取完矩阵所有元素；每次取走的各个元素只能是该元素所在行的行首或行尾；
每次取数时须从每行各取走一个元素，共 n 个，m 次后取完矩阵所有元素；每次取数都有一个得分值，为每行取数的得分之和，每行取数的得分 = 被取走的元素值*2i，其中 i 表示第 i 次取数（从 1 开始编号）；
每次取数时须从每行各取走一个元素，共 n 个，m 次后取完矩阵所有元素；游戏结束总得分为 m 次取数得分之和。

帅帅想请你帮忙写一个程序，对于任意矩阵，可以求出取数后的最大得分。

输入

    第 1 行为两个用空格隔开的整数 n 和 m, 1 <= n,m <= 90。
    第 2 ~ n+1 行为 n*m 矩阵，其中每行有 m 个用单个空格
    隔开的非负整数 a_{ij}, 0 <= a_{ij} <= 1000。

    2 3
    1 2 3
    3 4 2

输出

    输出仅包含 1 行，为一个整数，即输入矩阵取数后的最大得分。

    82

第 1 次：第 1 行取行首元素，第 2 行取行尾元素，本次得分为 1*21+2*21=6
第 2 次：两行均取行首元素，本次得分为 2*22+3*22=20
第 3 次：得分为 3*23+4*23=56。总得分为 6+20+56=82

首先，每行之间是互相独立的，因此可以分别求出每行的最大得分，最后相加起来。

设状态为 f(i,j)，表示单行的区间 [i,j] 的最大值，转移方程为

f(i,j) = max    {
                        f(i+1,j) + a(i)*2^x,
                        f(i,j-1) + a(j)*2^x
                },                                  1 <= x <= m

等价于

f(i,j) = 2 * max{
                        f(i+1,j) + a(i),
                        f(i,j-1) + a(j)
                }

同时，注意到，最大得分可能会非常大，因此需要用到大整数运算。预估一下最大得分，大概是 1000x2⁸⁰，用计算器算一下，有 28 位。

#include <stdio.h>
#include <memory.h>
#include <limits.h>

/* 一个数组元素表示4个十进制位，即数组是万进制的 */
#define BIGINT_RADIX 10000
#define RADIX_LEN 4
/* 1000*2^80 有 28 位 */
#define MAX_LEN (28/RADIX_LEN+1)  /* 整数的最大位数 */

/**
 * @brief 打印大整数.
 * @param[in] x 大整数，用数组表示，低位在低地址
 * @param[in] n 数组x的长度
 * @return 无
 */
void bigint_print(const int x[], const int n) {
    int i;
    int start_output = 0;  /* 用于跳过前导0 */
    for (i = n - 1; i >= 0; --i) {
        if (start_output) {  /* 如果多余的0已经都跳过，则输出 */
            printf("%04d", x[i]);
        } else if (x[i] > 0) {
            printf("%d", x[i]);
            start_output = 1; /* 碰到第一个非0的值，就说明多余的0已经都跳过 */
        }
    }

    if(!start_output) printf("0");  /* 当x全为0时 */
}

/**
 * @brief 一个32位整数转化为大整数bigint.
 * @param[in] n 32位整数
 * @param[out] x 大整数
 * @return 大整数
 */
int* int_to_bigint(int n, int x[]) {
    int i = 0;
    memset(x, 0, MAX_LEN * sizeof(int));
    while (n > 0) {
        x[i++] = n % BIGINT_RADIX;
        n /= BIGINT_RADIX;
    }
    return x;
}


/**
 * @brief 大整数比较.
 * @param[in] x x
 * @param[in] y y
 * @return x<y，返回-1，相等于返回0，大于返回1.
 */
int bigint_cmp(const int x[], const int y[]) {
    int i, lenx = 0, leny = 0;
    for (i = 0; i < MAX_LEN; i++) {
        if (x[i] != 0) lenx++;
        else break;
    }
    for (i = 0; i < MAX_LEN; i++) {
        if (y[i] != 0) leny++;
        else break;
    }
    if (lenx < leny) return -1;
    else if (lenx > leny) return 1;
    else {
        for (i = lenx - 1; i >= 0; i--) {
            if (x[i] == y[i]) continue;
            else if (x[i] > y[i]) return 1;
            else return -1;
        }
        return 0;
    }
}

/**
 * @brief 大整数加上普通整数.
 * @param[inout] x 大整数
 * @param[in] y 32位整数
 * @return 大整数
 */
int* bigint_add(int x[], const int y) {
    int i;

    x[0] += y;
    for (i = 0; i < MAX_LEN; i++) {
        if (x[i] >= BIGINT_RADIX) {
            x[i+1] += x[i] / BIGINT_RADIX;
            x[i] %= BIGINT_RADIX;
        }
    }
    return x;
}


/**
 * @brief 两个大整数相加, in place.
 * @param[inout] x x=x+y
 * @param[in] y y
 * @return 无
 */
void bigint_add1(int x[], const int y[]) {
    int i;
    int c = 0;

    for (i = 0; i < MAX_LEN; i++) {  /* 逐位相加 */
        const int tmp = x[i] + y[i] + c;
        x[i] = tmp % BIGINT_RADIX;
        c = tmp / BIGINT_RADIX;
    }
}

/**
 * @brief 大整数乘法, x = x*y.
 * @param[inout] x x
 * @param[in] y y
 * @return 无
 */
void bigint_mul(int x[], const int y) {
    int i;
    int c = 0; /* 保存进位 */

    for (i = 0; i < MAX_LEN; i++) { /*用y，去乘以x的各位*/
        const int tmp = x[i] * y + c;
        x[i] = tmp % BIGINT_RADIX;
        c = tmp / BIGINT_RADIX;
    }
}


#define MAX 80   /* n,m的最大值 */

int n, m;
int matrix[MAX][MAX];  /* 输入矩阵 */
/* f[i][j] 表示某一行区间[i,j]的最大值，转移方程
 * f[i][j] = f[i+1][j]+a[i]*2^x, f[i][j-1]+a[j]*2^x, 1<=x<=m
 * 等价于 f[i][j] = 2*max(f[i+1][j]+a[i], f[i][j-1]+a[j])
 */
int f[MAX][MAX][MAX_LEN];
int tmp[MAX_LEN];

/**
 * @brief 计算单行.
 * @param[in] a 某一行
 * @return 此行能获得的最大得分
 */
int* dp(int a[MAX], int l, int r) {
    if (l == r) {
        int_to_bigint(a[l] * 2, f[l][r]);
        return f[l][r];
    }
    if (f[l][r][0] >= 0) return f[l][r];

    if (l < r) {
        memcpy(f[l][r], dp(a, l+1, r), sizeof(f[l][r]));
        bigint_mul(bigint_add(f[l][r], a[l]), 2);
        memcpy(tmp, dp(a, l, r-1), sizeof(tmp));
        bigint_mul(bigint_add(tmp, a[r]), 2);

        if (bigint_cmp(f[l][r], tmp) < 0) memcpy(f[l][r], tmp, sizeof(tmp));
    }
    return f[l][r];
}

int main() {
    int i, j, result[MAX_LEN];
    scanf("%d%d", &n, &m);

    for (i = 0; i < n; i++) {
        for (j = 0; j < m; j++) {
            scanf("%d", &matrix[i][j]);
        }
    }

    memset(result, 0, sizeof(result));
    for (i = 0; i < n; i++) {
        memset(f, 0, sizeof(f));
        for (j = 0; j < m; j++) {
            int k;
            for (k = 0; k < m; k++) {
                f[j][k][0] = -1;
            }
        }
        bigint_add1(result, dp(matrix[i], 0, m-1));
    }
    bigint_print(result, MAX_LEN);
    return 0;
}

棋盘型动态规划 @

数字三角形（（略）见上面的 triangle）

过河卒 @

A 点有一个过河卒，需要走到目标 B 点。卒行走规则：可以向下、或者向右。同时在棋盘上的任一点有一个对方的马（如上图的 C 点），该马所在的点和所有跳跃一步可达的点称为对方马的控制点。例如上图 C 点上的马可以控制 9 个点（图中的 P1，P2 …P8 和 C）。卒不能通过对方马的控制点。

    0   1   2   3   4   5   6   7   8
    A-----------*-------*------------
1   |       *               *
2   |               C
3   |       *               *
4   |           *       *           B

棋盘用坐标表示，A 点（0，0）、B 点（n,m）(n,m 为不超过 20 的整数，并由键盘输入)，同样马的位置坐标是需要给出的（约定: C 不等于 A，同时 C 不等于 B）。现在要求你计算出卒从 A 点能够到达 B 点的路径的条数。

输入

    B 点的坐标（n,m）以及对方马的坐标（X,Y）

    6 6 3 2

输出

    一个整数（路径的条数）

    17

这是一个棋盘形动态规划。

设状态为 f[i][j]，表示从 (0,0) 到 (i,j) 的路径的条数，状态转移方程为

f[i][j] = f[i-1][j] + f[i][j-1]         if no horse at (i,j), else 0

#include <stdio.h>
#include <memory.h>

#define MAX 21

int n, m;
int x, y;                                                   // 马儿的坐标

int g[MAX][MAX];                                            // 棋盘，马儿以及马儿的控制点为1，其余为0
int f[MAX][MAX];                                            // f[i][j] = f[i-1][j] + f[i][j-1]

void dp() {
    memset(g, 0, sizeof(g));
    g[x][y] = 1;
    for( int i = 0; i < 8; ++i ) {
        static int dx[] = {-2, -1, 1, 2, 2, 1, -1, -2};     // 八个控制点，顺时针方向
        static int dy[] = {1, 2, 2, 1, -1, -2, -2, -1};
        if( 0 <= x+dx[i] && x+dx[i] <= n && 0 <= y+dy[i] && y+dy[i] <= n ) {
            g[x+dx[i]][y+dy[i]] = 1;
        }
    }

    memset(f, 0, sizeof(f));
    f[0][0] = 1;
    for( int i = 1; i <= n; ++i ) { if( !g[i][0] ) { f[i][0] = f[i-1][0]; } }   // 初始化边界
    for( int j = 1; j <= m; ++j ) { if( !g[0][j] ) { f[0][j] = f[0][j-1]; } }
    for( int i = 1; i <= n; ++i ) {
        for( int j = 1; j <= m; ++j ) {
            if( !g[i][j] ) {
                f[i][j] = f[i-1][j] + f[i][j-1];
            }
        }
    }
}

int main() {
    while( 4 == scanf("%d%d%d%d", &n, &m, &x, &y)) {
        dp();
        printf("%d\n", f[n][m]);
    }
    return 0;
}

传纸条 @

小渊和小轩是好朋友也是同班同学，他们在一起总有谈不完的话题。一次素质拓展活动中，班上同学安排做成一个 m 行 n 列的矩阵，而小渊和小轩被安排在矩阵对角线的两端，因此，他们就无法直接交谈了。幸运的是，他们可以通过传纸条来进行交流。纸条要经由许多同学传到对方手里，小渊坐在矩阵的左上角，坐标 (1,1)，小轩坐在矩阵的右下角，坐标 (m,n)。从小渊传到小轩的纸条只可以向下或者向右传递，从小轩传给小渊的纸条只可以向上或者向左传递。

在活动进行中，小渊希望给小轩传递一张纸条，同时希望小轩给他回复。班里每个同学都可以帮他们传递，但只会帮他们一次，也就是说如果此人在小渊递给小轩纸条的时候帮忙，那么在小轩递给小渊的时候就不会再帮忙。反之亦然。

还有一件事情需要注意，全班每个同学愿意帮忙的好感度有高有低（注意：小渊和小轩的好心程度没有定义，输入时用 0 表示），可以用一个 0 ~ 100 的自然数来表示，数越大表示越好心。小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条，即找到来回两条传递路径，使得这两条路径上同学的好心程度只和最大。现在，请你帮助小渊和小轩找到这样的两条路径。

输入

    输入的第一行有 2 个用空格隔开的整数 m 和 n，表示班
    里有 m 行 n 列 (1 <= m,n <= 50)。接下来的 m 行是一
    个 m*n 的矩阵，矩阵中第 i 行 j 列的整数表示坐在
    第 i 行 j 列的学生的好心程度。
    每行的 n 个整数之间用空格隔开

    3 3
    0 3 9
    2 8 5
    5 7 0

输出

    输出共一行，包含一个整数，表示来回两条路上参与传递
    纸条的学生的好心程度之和的最大值。

    34

这是一个棋盘形动态规划。用矩阵 int g[MAX][MAX] 存储输入数据，即每个学生的好心值。

题目等价为为从 (1,1) 传两张纸条到 (m,n)。每个纸条都是由上面或左边传递过来的，所以有四种情况。设状态为 f[i][j][k][l]，表示纸条一在 (i,j), 纸条二在 (k,l) 的好心程度之和，状态转移方程为

f[i][j][k][l]   =   max {
                            f[i-1][j][k-1][l],
                            f[i-1][j][k][l-1],
                            f[i][j-1][k][l-1],
                            f[i][j-1][k-1][l]
                        }                       +   g[i][j] +   g[k][l];

(i,j-1) ---+   +--- (k-1,l)
            \ /
             x
            / \
(i-1,j) ---+   +--- (k,l-1)

#include <cstdio>
#include <vector>

using namespace std;

void dp( const vector<vector<int> > &goodness, vector<vector<vector<vector<int> > > > &table ) {
    int m = goodness.size();
    int n = goodness[0].size();
    const vector<vector<int> >              &g = goodness;
    vector<vector<vector<vector<int> > > >  &f = table;
    for( int i = 0; i < m; ++i ) {
        for( int j = 0; j < n; ++j ) {
            for( int k = 0; k < m; ++k ) {
                for( int l = 0; l < n; ++l ) {
                    // (i-1,j), (k-1, l)
                    if( i > 0 && k > 0 && (i != k || j != l) ) {
                        f[i][j][k][l] = max(    f[i][j][k][l],
                                                f[i-1][j][k-1][l] + g[i][j]+g[k][l] );
                    }
                    // (i-1,j), (k, l-1)
                    if( i > 0 && l < n && (i-1 != k || j != l-1) ) {
                        f[i][j][k][l] = max(    f[i][j][k][l],
                                                f[i-1][j][k][l-1] + g[i][j]+g[k][l] );
                    }
                    // (i,j-1), (k, l-1)
                    if( j > 0 && l > 0 && (i != k || j != l) ) {
                        f[i][j][k][l] = max(    f[i][j][k][l],
                                                f[i][j-1][k][l-1] + g[i][j]+g[k][l] );
                    }
                    // (i,j-1), (k-1, l)
                    if( j > 0 && k > 0 && (i != k-1 || j-1 != l) ) {
                        f[i][j][k][l] = max(    f[i][j][k][l],
                                                f[i][j-1][k-1][l] + g[i][j]+g[k][l] );
                    }
                }
            }
        }
    }
}

int main() {
    int m, n;
    while( 2 == scanf("%d%d", &m, &n) ) {
        vector<vector<int> > goodness( m, vector<int>(n) );
        for( int i = 0; i < m; ++i ) {
            for( int j = 0; j < n; ++j ) {
                scanf( "%d", &goodness[i][j] );
            }
        }
        vector<vector<vector<vector<int> > > >
            table(  m,
                    vector<vector<vector<int> > >( n,
                                                   vector<vector<int> >( m, vector<int>(n, 0) ) ) );
        dp( goodness, table );
        printf( "%d\n", table[m-1][n-1][m-1][n-1] );
    }
    return 0;
}

TODO: 本题可以优化为三维

for( int i = 0; i < m; ++i ) {
    for( int j = 0; j < n; ++j ) {
        for( int k = 0; k < m; ++k ) {
            for( int l = 0; l < n; ++l ) {
                printf( "%p ", &table[i][j][k][l] );
            }
        }
        printf("\n");
    }
}

0x19464e0 0x19464e4 0x19464e8 0x1946500 0x1946504 0x1946508 0x1946520 0x1946524 0x1946528
0x1946590 0x1946594 0x1946598 0x19465b0 0x19465b4 0x19465b8 0x19465d0 0x19465d4 0x19465d8
0x1946640 0x1946644 0x1946648 0x1946660 0x1946664 0x1946668 0x1946680 0x1946684 0x1946688
0x1946740 0x1946744 0x1946748 0x1946760 0x1946764 0x1946768 0x1946780 0x1946784 0x1946788
0x19467f0 0x19467f4 0x19467f8 0x1946810 0x1946814 0x1946818 0x1946830 0x1946834 0x1946838
0x19468a0 0x19468a4 0x19468a8 0x19468c0 0x19468c4 0x19468c8 0x19468e0 0x19468e4 0x19468e8
0x19469a0 0x19469a4 0x19469a8 0x19469c0 0x19469c4 0x19469c8 0x19469e0 0x19469e4 0x19469e8
0x1946a50 0x1946a54 0x1946a58 0x1946a70 0x1946a74 0x1946a78 0x1946a90 0x1946a94 0x1946a98
0x1946b00 0x1946b04 0x1946b08 0x1946b20 0x1946b24 0x1946b28 0x1946b40 0x1946b44 0x1946b48

骑士游历 @

设有一个 n × m 的棋盘 (2 <= n <= 50, 2 <= m <= 50)，在棋盘上有一个中国象棋马。规定：

马只能走日字
马只能向右跳

问给定起点 (x1, y1) 和终点 (x2, y2)，求出马从 (x1, y1) 出发到 (x2, y2) 的合法路径条数。

输入

    第一行 2 个整数 n 和 m，第二行 4 个整数 x1,y1,x2,y2

    30 30
    1 15 3 15

输出

    合法路径条数

    2

这是一道棋盘型动态规划。

设状态为 f[i][j]，表示从起点 (x1,y1) 到 (i,j) 的合法路径条数，状态转移方程为

f[i][j] = f[i-1][j-2] + f[i-1][j+2] + f[i-2][j-1] + f[i-2][j+1]

注意，合法路径条数有可能非常大，32 位整数存不下，需要用 64 位整数。

#include <stdio.h>
#include <memory.h>
#include <stdint.h>

#define MAX  51                 // n, m 最大值

int n, m;
int x1, y1, x2, y2;
int64_t f[MAX+1][MAX+1];        // f[i][j] 表示从 (x1,y1) 到 (i,j) 的合法路径的条数

void dp() {
    memset(f, 0, sizeof(f));
    f[x1][y1] = 1;
    for( int i = x1+1; i <= x2; ++i ) {
        for ( int j = 1; j <= m; ++j ) {
            f[i][j] = f[i-1][j-2] + f[i-1][j+2] + f[i-2][j-1] + f[i-2][j+1];
        }
    }
}

int main() {
    scanf("%d%d", &n, &m);
    scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
    dp();
    // printf("%lld\n", f[x2][y2]);
    printf("%ld\n", f[x2][y2]);     // lld: long long int, ld: long int
    return 0;
}

划分型动态规划 @

乘积最大 @

设有一个长度为 N 的数字串，要求选手使用 K 个乘号将它分成 K+1 个部分，找出一种分法，使得这 K+1 个部分的乘积能够为最大。

举个例子：有一个数字串：312，当 N=3，K=1 时会有以下两种分法：

3x12 = 36
31x2 = 62

这时，符合题目要求的结果是：31x2 = 62。

输入

    输入共有两行：
    第一行共有 2 个自然数 N,K (6 <= N <= 40, 1 <= K <= 6)
    第二行是一个长度为 N 的数字串。

    4 2
    1231

输出

    输出最大乘积

    62

首先，本题可以用区间型动态规划的思路解决。设状态为 f[i][j][k]，表示 i 到 j 这一段用 k 个乘号的最大乘积，状态转移方程如下：

f[i][j][k] = max {
                        f[i][s][t] * f[s+1][j][k-t-1]
},                                                          i <= s < j, 0 <= t < k

复杂度是 O(N³K²)，代码如下：

#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>

#define MAXN 40
#define MAXK 6

int N, K;
char str[MAXN];

// f[i][j][k] 表示 i 到 j 这一段用 k 个乘号的最大乘积.
int64_t f[MAXN][MAXN][MAXK+1];

#define max(a,b) ((a)>(b)?(a):(b))

// 计算 str[l,r] 字符串的值，int64 可以过，不用高精度.
int64_t num(int l, int r) {
    int64_t ret = 0;
    for( int i = l; i <= r; ++r ) {
        ret = ret * 10 + str[i] - '0';
    }
    return ret;
}

// 区间型动态规划，复杂度是 O(n^3*k^2).
// f[i][j][k] = max(f[i][s][t] * f[s+1][j][k-t-1]), i <= s < j , 0 <= t < k
void dp() {
    memset(f, 0, sizeof(f));
    for( int i = 0; i < N; ++i ) {
        for( int j = i; j < N; ++j ) {
            f[i][j][0] = num(i, j);
        }
    }

    for( int i = 0; i < N; ++i ) {
        for( int j = i; j < N; ++j ) {
            for( int k = 1; k <= K; ++k ) {
                for( int s = i; s < j; ++s ) {
                    for( int t = 0; t < k; ++t ) {
                        f[i][j][k] = max(   f[i][j][k],
                                            f[i][s][t] * f[s + 1][j][k - t - 1] );
                    }
                }
            }
        }
    }
}

int main() {
    scanf( "%d%d", &N, &K );
    scanf( "%s", str );
    dp();
    printf( "%lld\n", f[0][N-1][K] );
    return 0;
}

复杂度是O(N²K)。代码如下。 @

尽管上面的代码可以 AC 了，但还有更高效的思路。设状态为 f[k][j]，表示在区间 [0,j] 放入 k 个乘号的最大乘积，状态转移方程如下：

f[k][j]=    max     {
                            f[k][j],
                            f[k-1][i]*num(i+1,j)
                    },                                  0 <= i < j

// wikioi 1017 乘积最大, http://www.wikioi.com/problem/1017
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>

#define MAXN 40
#define MAXK 6

int N, K;
char str[MAXN];

/** f[k][j]在区间[0,j]放入k个乘号的最大乘积. */
int64_t f[MAXK+1][MAXN];

#define max(a,b) ((a)>(b)?(a):(b))

/** 计算str[l,r]字符串的值，int64可以过，不用高精度. */
int64_t num(int l, int r) {
    int64_t ret = 0;
    int i;
    for (i = l; i <= r; i++) {
        ret = ret * 10 + str[i] - '0';
    }
    return ret;
}

/** 划分型型动态规划，复杂度是O(n^3*k^2). */
void dp() {
    int i, j, k;
    memset(f, 0, sizeof(f));
    for (j = 0; j < N; j++) {
        f[0][j] = num(0, j);
    }

    for (k = 1; k <= K; k++) {
        for (j = 0; j < N; j++) {
            for (i = 0; i < j; i++) {
                f[k][j] = max(f[k][j], f[k-1][i]*num(i+1, j));
            }
        }
    }
}

int main() {
    scanf("%d%d", &N, &K);
    scanf("%s", str);
    dp();
    printf("%lld\n", f[K][N-1]);
    return 0;
}

数的划分 @

将整数 n 分成 k 份，且每份不能为空，任意两种划分方案不能相同 (不考虑顺序)。

例如：n=7，k=3，下面三种划分方案被认为是相同的。

1 1 5
1 5 1
5 1 1

问有多少种不同的分法。

输入

    n, k (6<n <= 200,2 <= k <= 6)

    7 3

输出

    一个整数，即不同的分法。

    4

设状态为 f[k][i]，表示将整数 i 分成 k 份的方案数。有两种情况，一种划分中有至少一个 1，另外一种划分中所有的数都大于 1。对于第一种划分，去掉一个 1，就变成了一个于子问题 f[n-1][k-1]，对于第二种划分，把划分中的每个数都减去 1，就变成了一个子问题f[k][n-k]。因此，状态转移方程如下：

f[k][i] = f[k-1][i-1] + f[k][i-k]

// wikioi 1039 数的划分, http://www.wikioi.com/problem/1039
#include <stdio.h>
#include <memory.h>

#define MAXN 300
#define MAXK 10

int N, K;
int f[MAXK+1][MAXN+1];                      // f[k][i] 表示将整数 i 分成 k 份的方案数.

void dp() {                                 // 划分型动态规划，复杂度是 O(K*N)
    memset(f, 0, sizeof(f));
    for( int i = 1; i <= N; ++i ) {
        f[1][i] = 1;
        if( i <= K ) { f[i][i] = 1; }
    }

    for( int k = 2; k <= K; ++k ) {
        for( int i = k+1; i <= N; ++i ) {
            f[k][i] = f[k-1][i-1] + f[k][i-k];
        }
    }
}

int main() {
    scanf( "%d%d", &N, &K );
    dp();
    printf( "%d\n", f[K][N] );
    return 0;
}

树型动态规划 @

访问艺术馆 @

皮尔是一个出了名的盗画者，他经过数月的精心准备，打算到艺术馆盗画。艺术馆的结构，每条走廊要么分叉为二条走廊，要么通向一个展览室。皮尔知道每个展室里藏画的数量，并且他精确地测量了通过每条走廊的时间，由于经验老道，他拿下一副画需要 5 秒的时间。你的任务是设计一个程序，计算在警察赶来之前 (警察到达时皮尔回到了入口也算)，他最多能偷到多少幅画。

输入

    第 1 行是警察赶到得时间 s(s <= 600)，以秒为单位。第
    2 行描述了艺术馆得结构，是一串非负整数，成对地出现：
    每一对得第一个数是走过一条走廊得时间，第 2 个数是
    它末端得藏画数量；如果第 2 个数是 0，那么说明这条走
    廊分叉为两条另外得走廊。走廊的数目 <= 100。数据按照
    深度优先得次序给出，请看样例

    60
    7 0
        8 0
            3 1
            14 2
        10 0
            12 4
            6 2

输出

    输出偷到得画得数量

    2

设状态为 f[root][time]，表示在 root 节点，剩下 time 时间内能偷到的画数，则状态转移方程如下：

f[root][time]= max{
                            f[left][t] + f[right][ct-t]
},                                                              ct = time-T[root], 0 <= t <= ct

// wikioi 1163 访问艺术馆, http://www.wikioi.com/problem/1163/
#include <stdio.h>
#include <memory.h>

#define max(a,b) ((a)>(b)?(a):(b))
#define MAXN  1010                              // 走廊的最大数目

int LIMIT, T[MAXN], P[MAXN];                    // 警察到达时间，走廊时间，藏画数量
int n, L[MAXN], R[MAXN];                        // 二叉树: 节点个数，左孩子，右孩子, 0 位置未用

int f[MAXN][MAXN];                              // f[root][time] 表示在 root 节点，
                                                // 剩下 time 时间内能偷到的画数

// 输入的数据是前序遍历序列，依次读入，递归建树
int build_tree() {
    ++n;
    scanf("%d%d", &T[n], &P[n]);
    T[n] *= 2;                                  // 走廊花费时间要 x2, 因为还要出来
    int now = n;                                // 当前节点
    if( P[now] == 0 ) {
        L[now] = build_tree();                  // 建立节点 now 的左子树
        R[now] = build_tree();                  // 建立节点 now 的右子树
    }
    return now;
}

// 备忘录法.  root 开始节点, 剩余时间, return 偷到得画的数量
int dp( int root, int time ) {
    if( f[root][time] != -1 ) {
        return f[root][time];
    }
    if( !time ) {                       // no time left
        return f[root][time] = 0;
    }

    const int ct = time - T[root];      // 留给左右子节点的时间

    // 到达叶子节点，即展览室
    if( !L[root] && !R[root] ) {
        if ( P[root] * 5 <= ct ) {                  // 不能 tt / 5,因为时间够，但是可能画不够
            return f[root][time] = P[root];         // take all the paintings
        } else {
            return f[root][time] = ct / 5;          // take as much as you can
        }
    }

    f[root][time] = 0;
    for( int t = 0; t <= ct; ++t ) {
        int lp = dp( L[root], t );
        int rp = dp( R[root], ct - t );
        f[root][time] = max( f[root][time], lp + rp );  // update
    }
    return f[root][time];
}

int main() {
    scanf( "%d", &LIMIT );
    n = 0;
    build_tree();
    memset( f, -1, sizeof(f) );
    printf( "%d\n", dp( 1, LIMIT) );
    return 0;
}

没有上司的舞会 ♥️ @

Ural 大学有 N 个职员，编号为 1 ~ N。他们有从属关系，也就是说他们的关系就像一棵以校长为根的树，父结点就是子结点的直接上司。每个职员有一个快乐指数。现在有个周年庆宴会，要求与会职员的快乐指数最大。但是，没有职员愿和直接上司一起与会。

输入

    第一行一个整数 N (1 <= N <= 6000)。
    接下来 N 行，第 i+1 行表示 i 号职员的快乐指数 R_i (-128 <= R_i <= 127)。
    接下来 N-1 行，每行输入一对整数 L,K。表示 K 是 L 的直接上司。

    7
    1       1       1       1       1       1       1
    1 3     2 3     6 4     7 4     4 5     3 5

输出

    输出最大的快乐指数

    5

设状态为 f[k][0] 和 f[k][1]，f[k][0] 表示第 k 个人不参加时的最大值， f[k][1] 表示第 k 个人参加的最大值，则状态转移方程如下：

f[k][0] = sum_l max{ f[l][0], f[l][1] },            其中 k 是 l 的直接上司
f[k][1] = sum_l f[l][0] + r[k]                      r[k] is the happy value

// wikioi 1380 没有上司的舞会, http://www.wikioi.com/problem/1380
#include <stdio.h>
#include <string.h>

#define max(a,b) ((a)>(b)?(a):(b))
#define MAXN 6001                                           // 0 位置未用

int n;
int r[MAXN];                                                // 快乐指数

struct edge_t {                                             // 静态链表节点
    int v;
    int prev;                                               // 上一条边，倒着串起来
};

edge_t edge[MAXN-1];                                        // 多个静态链表在一
                                                            // 个数组里，实质上是树的孩子表示法

int head[MAXN];                                             // head[root]指向表头，即最后一条边

bool has_boss[MAXN];                                        // has_boss[i] 表示第 i 个人是否有上司

int f[MAXN][2];

int cnt;                                                    // 边个数 - 1
void add_edge( int u, int v ) {
    edge[cnt].v = v;                                        // v->u, v->head[u]
    edge[cnt].prev = head[u];
    head[u] = cnt;                                          // u->v: edge[head[u]].v
    ++cnt;
}

void printGraph( int x, int y ) {
    fprintf( stderr, "\nGraph after %d->%d:\n", x, y );
    for( int k = 0; k < 6001; ++k ) {
        int p = head[k];
        if( p == -1 ) { continue; }
        fprintf( stderr, "head[%d]:", k );
        for( ; p != -1; p = edge[p].prev ) {
            int v = edge[p].v;
            fprintf( stderr, " %d", v );
        }
        fprintf( stderr, "\n" );
    }
}

void dp( int k ) {
    f[k][1] = r[k];
    f[k][0] = 0;
    for( int p = head[k]; p != -1; p = edge[p].prev ) {
        int l = edge[p].v;
        dp(l);
        f[k][1] += f[l][0];
        f[k][0] = f[k][0] + max(f[l][1],f[l][0]);
    }
}

int solve() {
    memset(f, 0, sizeof(f));
    int k;
    for( k = 1; k <= n; ++k ) {
        if( !has_boss[k] ) {
            break;
        }
    }
    dp(k);
    return max(f[k][0], f[k][1]);                           // cool!
}

int main() {
    scanf( "%d", &n );
    for( int i = 1; i <= n; ++i ) {
        scanf("%d", &r[i] );
    }

    cnt = 0;
    memset( has_boss, 0, sizeof(has_boss) );
    memset( head,    -1, sizeof(head) );
    for( int i = 0; i < n-1; ++i ) {
        int x, y;
        scanf( "%d%d", &x, &y );
        has_boss[x] = 1;
        add_edge( y, x );               //    x   ->  y
        printGraph( x, y );
    }
    printf("%d\n", solve());
    return 0;
}

log in stderr, if you don’t understand it. @

Graph after 1->3:
head[3]: 1

Graph after 2->3:
head[3]: 2 1

Graph after 6->4:
head[3]: 2 1
head[4]: 6

Graph after 7->4:
head[3]: 2 1
head[4]: 7 6

Graph after 4->5:
head[3]: 2 1
head[4]: 7 6
head[5]: 4

Graph after 3->5:
head[3]: 2 1
head[4]: 7 6
head[5]: 3 4

最大子矩形 @

在一个给定的矩形网格中有一些障碍点，要找出网格内部不包含任何障碍点，且边界与坐标轴平行的最大子矩形。

遇到求矩形面积，一般把左上角设置为坐标原点，这与数学中的坐标系不同。

解决方法参考 “浅谈用极大化思想解决最大子矩形问题”

方法一是一种暴力枚举法，方法二是一种动规法。

奶牛浴场 @

由于 John 建造了牛场围栏，激起了奶牛的愤怒，奶牛的产奶量急剧减少。为了讨好奶牛，John 决定在牛场中建造一个大型浴场。但是 John 的奶牛有一个奇怪的习惯，每头奶牛都必须在牛场中的一个固定的位置产奶，而奶牛显然不能在浴场中产奶，于是，John 希望所建造的浴场不覆盖这些产奶点。这回，他又要求助于 Clevow 了。你还能帮助 Clevow 吗？

John 的牛场和规划的浴场都是矩形。浴场要完全位于牛场之内，并且浴场的轮廓要与牛场的轮廓平行或者重合。浴场不能覆盖任何产奶点，但是产奶点可以位于浴场的轮廓上。

Clevow 当然希望浴场的面积尽可能大了，所以你的任务就是帮她计算浴场的最大面积。

输入

    输入文件的第一行包含两个整数 L 和 W (1 <= L,W <= 30000)，
    分别表示牛场的长和宽。文件的第二行包含一个整数 n(0 <= n <= 5000)，
    表示产奶点的数量。以下 n 行每行包含两个整数 x 和 y，
    表示一个产奶点的坐标。所有产奶点都位于牛场内，
    即：0 <= x <= l, 0 <= y <= w。

    10 10
    4
    1 1
    9 1
    1 9
    9 9

输出

    输出文件仅一行，包含一个整数 S，表示浴场的最大面积。

    80

方法一是暴力枚举法，方法二是动规法。这里使用方法二，需要先做一定的预处理。由于第二种算法复杂度与牛场的面积有关，而题目中牛场的面积很大（30000×30000），因此需要对数据进行离散化处理。离散化后矩形的大小降为 S×S，所以时间复杂度为 O(S2)，空间复杂度为 O(S)。需要注意的是，为了保证算法能正确执行，把 (0,0) 和 (m,n) 设置为产奶点，相当于加上了一个“虚拟边界”。

// OJ: https://vijos.org/p/1055
#include <string.h>
#include <stdio.h>
#include <stdlib.h>
#include <vector>

using namespace std;

#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))

int L, W;                   //            W
                            //        +------> y
                            //        |
                            //     L  |
                            //        |
                            //        V x

#define MAXN 5001
int n;                      // n个产奶点
int x[MAXN], y[MAXN];       // 产奶点坐标

int int_cmp( const void *a, const void *b ) {
    const int *ia = (const int*) a;
    const int *ib = (const int*) b;
    return *ia - *ib;
}

int binary_search( int A[], int n, int target ) {
    int low = 0, high = n-1, mid;
    while( low <= high ) {
        mid = (low+high)/2;
        if( A[mid] < target ) {
            low = mid+1;
        } else if( A[mid] > target ) {
            high = mid-1;
        } else {
            return mid;
        }
    }
    return -1;
}

int max_submatrix(const int L, const int W,
        const int x[], const int y[], int n) {
    vector<int> aa( n+1 );
    // int *a = (int*) malloc((n + 1) * sizeof(int));
    int *a = &aa[0];
    int *b = (int*) malloc((n + 1) * sizeof(int));
    int la = n, lb = n;
    int i, j;
    int lm, rm; // 左边界，右边界
    int result = 0, temp;
    int **v;  // 新的01矩阵，1表示障碍点
    int *h;  // 高度
    int *l;  // 左边界
    int *r;  // 右边界

    memcpy(a, x, n * sizeof(int));
    memcpy(b, y, n * sizeof(int));
    a[la++] = 0;
    b[lb++] = 0;
    a[la++] = L;
    b[lb++] = W;

    // 去重
    qsort(a, la, sizeof(int), int_cmp);
    qsort(b, lb, sizeof(int), int_cmp);
    for (j = 1, i = 1; i < la; i++) { // 去重
        if (a[i] != a[i - 1])
            a[j++] = a[i];
    }
    la = j;
    for (j = 1, i = 1; i < lb; i++) { // 去重
        if (b[i] != b[i - 1])
            b[j++] = b[i];
    }
    lb = j;
    h = (int*) malloc(lb * sizeof(int));
    l = (int*) malloc(lb * sizeof(int));
    r = (int*) malloc(lb * sizeof(int));

    // 计算 v矩阵
    v = (int**) malloc(la * sizeof(int*));
    for (i = 0; i < la; i++) {
        v[i] = (int*) calloc(lb, sizeof(int));
    }
    for (i = 0; i < n; i++) {
        int ia, ib;
        ia = binary_search(a, la, x[i]);
        ib = binary_search(b, lb, y[i]);
        v[ia][ib] = 1; //标记障碍点
    }

    // 初始化
    for (i = 0; i < lb; i++) {
        l[i] = 0;
        r[i] = W;
        h[i] = 0;
    }

    for (i = 1; i < la; i++) { // 从上到下
        lm = 0;
        for (j = 0; j < lb; j++) { // 从左到右计算l[j]
            if (!v[i - 1][j]) {  //如果上一个不是障碍点
                h[j] = h[j] + a[i] - a[i - 1]; //高度累加
                // l[i][j]=max(l[i-1][j] , 左边第一个障碍点(i-1,j)的位置)
                l[j] = max(l[j], lm);
            } else {  //如果上一个点是障碍点
                h[j] = a[i] - a[i - 1]; //高度重新计算
                l[j] = 0;
                r[j] = W;
                lm = b[j]; //更新(i-1,j)左边第一个障碍点的位置
            }
        }
        rm = W;
        for (j = lb - 1; j >= 0; j--) {  //  从右到左计算r[j]
            //r[i][j]=min(r[i-1][j] , (i-1,j)右边第一个障碍点的位置)
            r[j] = min(r[j], rm);
            temp = h[j] * (r[j] - l[j]);
            result = max(result, temp);  //计算最优解
            if (v[i - 1][j]) //如果该点是障碍点，更新(i-1,j)右边第一个障碍点的位置
                rm = b[j];
        }
    }
    // 计算横条的面积
    for (i = 1; i < la; i++) {
        temp = W * (a[i] - a[i - 1]);
        result = max(result, temp);
    }

    // free(a);
    free(b);
    for (i = 0; i < la; i++) {
        free(v[i]);
    }
    free(v);
    free(h);
    free(l);
    free(r);
    return result;
}

int main() {
    int i;
    while (scanf("%d%d", &L, &W) == 2) {
        scanf("%d", &n);
        for (i = 0; i < n; i++) {
            scanf("%d%d", &x[i], &y[i]);
        }

        printf("%d\n", max_submatrix(L, W, x, y, n));
    }
    return 0;
}

最大全 1 子矩阵 @

给定一个 m * n 的 01 矩阵，求最大的全 1 子矩阵。

输入

    输入包含多组测试用例。每组测试用例第一行包含两个整
    数 m 和 n (1 <= m,n <= 2000)，接下来是 m 行数据，每
    行 n 个元素。

    2 2
    0 0
    0 0
    4 4
    0 0 0 0
    0 1 1 0
    0 1 1 0
    0 0 0 0
    8 8
    0   1   0   0   0   0   1   1
    1   1   1   0   0   0   1   1
    1   1   1   0   0   0   0   0
    1   1   1   0   1   1   1   1
    0   0   0   0   1   1   1   1
    0   0   0   0   1   1   1   1
    0   0   0   0   1   1   1   1
    0   0   0   0   1   1   1   1

输出

    对每个测试用例，输出最大全 1 子矩阵的 1 的个数。如
    果输入的矩阵是全 0，则输出 0.

    0
    4
    20

注意，上一题算的是面积，这一题算的是个数，在某些细节上处理不同。

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <vector>

using namespace std;

int lagest_rectangle( vector<vector<int> > &matrix, int m, int n ) {
    vector<int> H( n, 0 );                              // 高度
    vector<int> L( n, 0 );                              // 左边界
    vector<int> R( n, n );                              // 右边界

    int ret = 0;
    for( int i = 0; i < m; ++i ) {
        int left = 0, right = n;
        // calculate L(i, j) from left to right
        for( int j = 0; j < n; ++j ) {
            if( matrix[i][j] == 1 ) {
                ++H[j];
                L[j] = max( L[j], left );               // rightify L
            } else {
                left = j + 1;
                H[j] = 0;
                L[j] = 0;
                R[j] = n;
            }
        }
        // calculate R(i, j) from right to left
        for( int j = n - 1; j >= 0; --j ) {
            if( matrix[i][j] == 1 ) {
                R[j] = min( R[j], right );              // leftify R
                ret = max( ret, H[j]*(R[j]-L[j]) );     // larger area
            } else {
                right = j;
            }
        }
    }

    return ret;
}

int main() {
    int m, n;
    while( 2 == scanf("%d%d", &m, &n) ) {
        vector<vector<int> > matrix( m, vector<int>(n) );
        for( int i = 0; i < m; ++i ) {
            for( int j = 0; j < n; ++j ) {
                scanf( "%d", &matrix[i][j] );
            }
        }
        printf( "%d\n", lagest_rectangle(matrix, m, n) );
    }
    return 0;
}

// ret = max( ret, H[j]*(R[j]-L[j]) );     // larger area

int area = H[j]*(R[j]-L[j]);
if( area > ret ) {
    printf( "Area: %d, j= %d, L[j]: %d, R[j]: %d, H[j]: %d\n",
            area, j, L[j], R[j], H[j] );
    ret = area;
}

8   8
0   1   0   0   0   0   1   1
1   1   1   0   0   0   1   1
1   1   1   0   0   0   0   0
1   1   1   0   1   1   1   1
0   0   0   0   1   1   1   1
0   0   0   0   1   1   1   1
0   0   0   0   1   1   1   1
0   0   0   0   1   1   1   1

Area: 2,    j= 7, L[j]: 6, R[j]: 8, H[j]: 1
Area: 4,    j= 7, L[j]: 6, R[j]: 8, H[j]: 2
Area: 6,    j= 2, L[j]: 0, R[j]: 3, H[j]: 2
Area: 9,    j= 2, L[j]: 0, R[j]: 3, H[j]: 3
Area: 12,   j= 7, L[j]: 4, R[j]: 8, H[j]: 3
Area: 16,   j= 7, L[j]: 4, R[j]: 8, H[j]: 4
Area: 20,   j= 7, L[j]: 4, R[j]: 8, H[j]: 5

DAG 上的动态规划 @

啥是 DAG @
In mathematics and computer science, a directed acyclic graph (DAG, /dæɡ/), is a finite directed graph with no directed cycles.

refs and see also
- Directed acyclic graph - Wikipedia, the free encyclopedia

小结与应用举例 @

9-1 UVa1025 A Spy in the Metro uva1025.cpp @

// UVa1025 A Spy in the Metro
// Rujia Liu
#include<iostream>
#include<cstring>
using namespace std;

const int maxn = 50 + 5;
const int maxt = 200 + 5;
const int INF = 1000000000;

// has_train[t][i]表示时刻t，在车站i是否有往右开的火车
int t[maxn], has_train[maxt][maxn];
int dp[maxt][maxn];

int main() {
    int kase = 0, n, T;
    while(cin >> n >> T && n) {
        int M1, M2, d;
        for(int i = 1; i <= n-1; i++) cin >> t[i];

        // 预处理，计算has_train数组
        memset(has_train, 0, sizeof(has_train));
        cin >> M1;
        while(M1--) {
            cin >> d;
            for(int j = 1; j <= n-1; j++) {
                if(d <= T) has_train[d][j] = 1;
                d += t[j];
            }
        }
        cin >> M2;
        while(M2--) {
            cin >> d;
            for(int j = n-1; j >= 1; j--) {
                if(d <= T) has_train[d][j+1] = 1;
                d += t[j];
            }
        }

        // DP主过程
        for(int i = 1; i <= n-1; i++) dp[T][i] = INF;
        dp[T][n] = 0;

        for(int i = T-1; i >= 0; i--)
            for(int j = 1; j <= n; j++) {
                dp[i][j] = dp[i+1][j] + 1; // 等待一个单位
                if(j < n && has_train[i][j] && i+t[j] <= T)
                    dp[i][j] = min(dp[i][j], dp[i+t[j]][j+1]); // 右
                if(j > 1 && has_train[i][j] && i+t[j-1] <= T)
                    dp[i][j] = min(dp[i][j], dp[i+t[j-1]][j-1]); // 左
            }

        // 输出
        cout << "Case Number " << ++kase << ": ";
        if(dp >= INF) cout << "impossible\n";
        else cout << dp << "\n";
    }
    return 0;
}

9-2 UVa437 The Tower of Babylon UVa437.cpp @

// UVa437 The Tower of Babylon
// Rujia Liu
// 算法：DAG上的最长路，状态为(idx, k)，即当前顶面为立方体idx，其中第k条边（排序后）为高
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

#define REP(i,n) for(int i = 0; i < (n); i++)

const int maxn = 30 + 5;
int n, blocks[maxn], d[maxn];

void get_dimensions(int* v, int b, int dim) {
    int idx = 0;
    REP(i,3) if(i != dim) v[idx++] = blocks[b][i];
}

int dp(int i, int j) {
    int& ans = d[i][j];
    if(ans > 0) return ans;
    ans = 0;
    int v, v2;
    get_dimensions(v, i, j);
    REP(a,n) REP(b,3) {
        get_dimensions(v2, a, b);
        if(v2 < v && v2 < v) ans = max(ans, dp(a,b));
    }
    ans += blocks[i][j];
    return ans;
}

int main() {
    int kase = 0;
    while(scanf("%d", &n) == 1 && n) {
        REP(i,n) {
            REP(j,3) scanf("%d", &blocks[i][j]);
            sort(blocks[i], blocks[i]+3);
        }
        memset(d, 0, sizeof(d));
        int ans = 0;
        REP(i,n) REP(j,3) ans = max(ans, dp(i,j));
        printf("Case %d: maximum height = %d\n", ++kase, ans);
    }
    return 0;
}

9-3 UVa1347 Tour uva1347.cpp @

// UVa1347 Tour
// Rujia Liu
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;

const int maxn = 50 + 5;
double x[maxn], y[maxn], dist[maxn][maxn], d[maxn][maxn];

int main() {
    int n;
    while(scanf("%d", &n) == 1) {
        for(int i = 1; i <= n; i++)
            scanf("%lf%lf", &x[i], &y[i]);
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= n; j++)
                dist[i][j] = sqrt((x[i]-x[j])*(x[i]-x[j]) + (y[i]-y[j])*(y[i]-y[j]));

        for(int i = n-1; i >= 2; i--)
            for(int j = 1; j < i; j++) {
                if(i == n-1) d[i][j] = dist[i][n] + dist[j][n]; // 边界
                else d[i][j] = min(dist[i][i+1] + d[i+1][j], dist[j][i+1] + d[i+1][i]);
            }
        printf("%.2lf\n", dist + d);
    }
    return 0;
}

多阶段决策问题 @

多段图的最短路 @

9-4 UVa116 Unidirectional TSP UVa116.cpp @

// UVa116 Unidirectional TSP
// Rujia Liu
// 算法：多段图的动态规划。因为要字典序最小，所以倒着来，设d[i][j]为从(i,j)到最后一列的最小开销，则d[i][j]=a[i][j]+max(d[i+1][j+1],d[i-1][j+1])
#include<cstdio>
#include<algorithm>
using namespace std;

const int maxn = 100 + 5;
const int INF = 1000000000;
int m, n, a[maxn][maxn], d[maxn][maxn], next[maxn][maxn];

int main() {
    while(scanf("%d%d", &m, &n) == 2 && m) {
        for(int i = 0; i < m; i++)
            for(int j = 0; j < n; j++)
                scanf("%d", &a[i][j]);

        int ans = INF, first = 0;
        for(int j = n-1; j >= 0; j--) {
            for(int i = 0; i < m; i++) {
                if(j == n-1) d[i][j] = a[i][j];
                else {
                    int rows = {i, i-1, i+1};
                    if(i == 0) rows = m-1;
                    if(i == m-1) rows = 0;
                    sort(rows, rows+3);
                    d[i][j] = INF;
                    for(int k = 0; k < 3; k++) {
                        int v = d[rows[k]][j+1] + a[i][j];
                        if(v < d[i][j]) { d[i][j] = v; next[i][j] = rows[k]; }
                    }
                }
                if(j == 0 && d[i][j] < ans) { ans = d[i][j]; first = i; }
            }
        }
        printf("%d", first+1);
        for(int i = next[first], j = 1; j < n; i = next[i][j], j++) printf(" %d", i+1);
        printf("\n%d\n", ans);
    }
    return 0;
}

0-1 背包问题 @

9-5 UVa12563 Jin Ge Jin Qu [h]ao UVa12563.cpp @

// UVa12563 Jin Ge Jin Qu [h]ao
// Rujia Liu
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int maxn = 50 + 5;
const int INF = 1000000000;

// d[i][j]: maximal number of songs from first i songs, whose total length is exactly j
int n, t, len[maxn], d[maxn*180+678];

int main() {
    int T;
    scanf("%d", &T);
    for(int kase = 1; kase <= T; kase++) {
        scanf("%d%d", &n, &t);
        for(int i = 1; i <= n; i++) scanf("%d", &len[i]);

        for(int i = 0; i < t; i++) d[i] = -1;
        d = 0;

        int p = 1, ans = 0;
        for(int i = 1; i <= n; i++) {
            for(int j = 0; j < t; j++) {
                d[p][j] = d[p^1][j];
                if(j >= len[i] && d[p^1][j - len[i]] >= 0)
                    d[p][j] = max(d[p][j], d[p^1][j - len[i]] + 1);
                ans = max(ans, d[p][j]);
            }
            p ^= 1;
        }
        for(int i = t-1; i >= 0; i--)
            if(d[p^1][i] == ans) {
                printf("Case %d: %d %d\n", kase, ans + 1, i + 678);
                break;
            }
    }
    return 0;
}

更多经典模型 @

线性结构上的动态规划 @

9-6 UVa11400 Lighting System Design uva11400.cpp @

// UVa11400 Lighting System Design
// Rujia Liu
#include<iostream>
#include<algorithm>
using namespace std;

const int maxn = 1000 + 5;

struct Lamp {
    int v, k, c, l;
    bool operator < (const Lamp& rhs) const {
        return v < rhs.v;
    }
} lamp[maxn];

int n, s[maxn], d[maxn];

int main() {
    while(cin >> n && n) {
        for(int i = 1; i <= n; i++)
            cin >> lamp[i].v >> lamp[i].k >> lamp[i].c >> lamp[i].l;
        sort(lamp+1, lamp+n+1);
        s = 0;
        for(int i = 1; i <= n; i++) s[i] = s[i-1] + lamp[i].l;
        d = 0;
        for(int i = 1; i <= n; i++) {
            d[i] = s[i] * lamp[i].c + lamp[i].k; // 前i个灯泡全买类型i
            for(int j = 1; j <= i; j++)
                d[i] = min(d[i], d[j] + (s[i] - s[j]) * lamp[i].c + lamp[i].k);
        }
        cout << d[n] << "\n";
    }
    return 0;
}

9-7 UVa11584 Partitioning by Palindromes UVa11584.cpp @

// UVa11584 Partitioning by Palindromes
// Rujia Liu
// This code is slightly different from the book.
// It uses memoization to judge whether s[i..j] is a palindrome.
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int maxn = 1000 + 5;
int n, kase, vis[maxn][maxn], p[maxn][maxn], d[maxn];
char s[maxn];

int is_palindrome(int i, int j) {
    if(i >= j) return 1;
    if(s[i] != s[j]) return 0;

    if(vis[i][j] == kase) return p[i][j];
    vis[i][j] = kase;
    p[i][j] = is_palindrome(i+1, j-1);
    return p[i][j];
}

int main() {
    int T;
    scanf("%d", &T);
    memset(vis, 0, sizeof(vis));
    for(kase = 1; kase <= T; kase++) {
        scanf("%s", s+1);
        n = strlen(s+1);
        d = 0;
        for(int i = 1; i <= n; i++) {
            d[i] = i+1;
            for(int j = 0; j < i; j++)
                if(is_palindrome(j+1, i)) d[i] = min(d[i], d[j] + 1);
        }
        printf("%d\n", d[n]);
    }
    return 0;
}

9-8 UVa1625 Color Length UVa1625.cpp @

// UVa1625 Color Length
// Rujia Liu

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int maxn = 5000 + 5;
const int INF = 1000000000;

char p[maxn], q[maxn]; // starts from position 1
int sp, sq, ep, eq; // sp[i] start positions of character i in p
int d[maxn], c[maxn]; // c[i][j]: how many "incomplete" colors in the mixed sequence

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        scanf("%s%s", p+1, q+1);

        int n = strlen(p+1);
        int m = strlen(q+1);
        for(int i = 1; i <= n; i++) p[i] -= 'A';
        for(int i = 1; i <= m; i++) q[i] -= 'A';

        // calculate s and e
        for(int i = 0; i < 26; i++) { sp[i] = sq[i] = INF; ep[i] = eq[i] = 0; }
        for(int i = 1; i <= n; i++) {
            sp[p[i]] = min(sp[p[i]], i);
            ep[p[i]] = i;
        }
        for(int i = 1; i <= m; i++) {
            sq[q[i]] = min(sq[q[i]], i);
            eq[q[i]] = i;
        }

        // dp
        int t = 0;
        memset(c, 0, sizeof(c));
        memset(d, 0, sizeof(d));
        for(int i = 0; i <= n; i++){
            for(int j = 0; j <= m; j++){
                if(!i && !j) continue;

                // calculate d
                int v1 = INF, v2 = INF;
                if(i) v1 = d[t^1][j] + c[t^1][j]; // remove from p
                if(j) v2 = d[t][j - 1] + c[t][j - 1]; // remove from q
                d[t][j] = min(v1, v2);

                // calculate c
                if(i) {
                    c[t][j] = c[t^1][j];
                    if(sp[p[i]] == i && sq[p[i]] > j) c[t][j]++;
                    if(ep[p[i]] == i && eq[p[i]] <= j) c[t][j]--;
                } else if(j) {
                    c[t][j] = c[t][j - 1];
                    if(sq[q[j]] == j && sp[q[j]] > i) c[t][j]++;
                    if(eq[q[j]] == j && ep[q[j]] <= i) c[t][j]--;
                }
            }
            t ^= 1;
        }
        printf("%d\n", d[t^1][m]);
    }
    return 0;
}

9-9 UVa10003 Cutting Sticks UVa10003.cpp @

// UVa10003 Cutting Sticks
// Rujia Liu
// 算法：设d[i][j]为切割小木棍i~j的最优费用，则d[i][j]=min{d[i][k]+d[k][j]}+a[j]-a[i]。最后的a[j]-a[i]是第一刀的费用。然后分成i~k和k~j两部分。
#include<cstdio>
#include<cstring>
using namespace std;

const int maxn = 50 + 5;
int n, L, a[maxn], vis[maxn][maxn], d[maxn][maxn];

int dp(int i, int j) {
    if(i >= j - 1) return 0;
    if(vis[i][j]) return d[i][j];
    vis[i][j] = 1;
    int& ans = d[i][j];
    ans = -1;
    for(int k = i+1; k <= j-1; k++) {
        int v = dp(i,k) + dp(k,j) + a[j] - a[i];
        if(ans < 0 || v < ans) ans = v;
    }
    return ans;
}

int main() {
    while(scanf("%d%d", &L, &n) == 2 && L) {
        for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
        a = 0; a[n+1] = L;
        memset(vis, 0, sizeof(vis));
        printf("The minimum cutting is %d.\n", dp(0, n+1));
    }
    return 0;
}

9-10 UVa1626 Brackets Sequence UVa1626.cpp -< @

// LA2451 Brackets Sequence
// Rujia Liu
// 算法：形如(S)或者[S]，转移到d(S)，然后分成AB，转移到d(A)+d(B)。注意(S, [S, )S之类全部属于第二种转移。
// 注意输入有空行。
// 本程序是递推解法
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int maxn = 100 + 5;
char S[maxn];
int n, d[maxn][maxn];

bool match(char a, char b) {
    return (a == '(' && b == ')') || (a == '[' && b == ']');
}

void dp() {
    for(int i = 0; i < n; i++) {
        d[i+1][i] = 0;
        d[i][i] = 1;
    }
    for(int i = n-2; i >= 0; i--)
        for(int j = i+1; j < n; j++) {
            d[i][j] = n;
            if(match(S[i], S[j])) d[i][j] = min(d[i][j], d[i+1][j-1]);
            for(int k = i; k < j; k++)
                d[i][j] = min(d[i][j], d[i][k] + d[k+1][j]);
        }
}

void print(int i, int j) {
    if(i > j) return ;
    if(i == j) {
        if(S[i] == '(' || S[i] == ')') printf("()");
        else printf("[]");
        return;
    }
    int ans = d[i][j];
    if(match(S[i], S[j]) && ans == d[i+1][j-1]) {
        printf("%c", S[i]); print(i+1, j-1); printf("%c", S[j]);
        return;
    }
    for(int k = i; k < j; k++)
        if(ans == d[i][k] + d[k+1][j]) {
            print(i, k); print(k+1, j);
            return;
        }
}

void readline(char* S) {
    fgets(S, maxn, stdin);
}

int main() {
    int T;

    readline(S);
    sscanf(S, "%d", &T);
    readline(S);

    while(T--) {
        readline(S);
        n = strlen(S) - 1;
        memset(d, -1, sizeof(d));
        dp();
        print(0, n-1);
        printf("\n");
        if(T) printf("\n");
        readline(S);
    }
    return 0;
}

9-11 UVa1331 Minimax Triangulation UVa1331.cpp @

// UVa1331 Minimax Triangulation
// Rujia Liu
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<cstring>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;

const double eps = 1e-10;
int dcmp(double x) {
    if(fabs(x) < eps) return 0; else return x < 0 ? -1 : 1;
}

struct Point {
    double x, y;
    Point(double x=0, double y=0):x(x),y(y) { }
};

typedef Point Vector;

Vector operator + (const Vector& A, const Vector& B) { return Vector(A.x+B.x, A.y+B.y); }
Vector operator - (const Point& A, const Point& B) { return Vector(A.x-B.x, A.y-B.y); }
Vector operator * (const Vector& A, double p) { return Vector(A.x*p, A.y*p); }

bool operator < (const Point& a, const Point& b) {
    return a.x < b.x || (a.x == b.x && a.y < b.y);
}

bool operator == (const Point& a, const Point &b) {
    return dcmp(a.x-b.x) == 0 && dcmp(a.y-b.y) == 0;
}

double Dot(const Vector& A, const Vector& B) { return A.x*B.x + A.y*B.y; }
double Cross(const Vector& A, const Vector& B) { return A.x*B.y - A.y*B.x; }
double Length(Vector A) { return sqrt(Dot(A, A)); }

bool SegmentProperIntersection(const Point& a1, const Point& a2, const Point& b1, const Point& b2) {
    double c1 = Cross(a2-a1,b1-a1), c2 = Cross(a2-a1,b2-a1),
           c3 = Cross(b2-b1,a1-b1), c4=Cross(b2-b1,a2-b1);
    return dcmp(c1)*dcmp(c2)<0 && dcmp(c3)*dcmp(c4)<0;
}

bool OnSegment(const Point& p, const Point& a1, const Point& a2) {
    return dcmp(Cross(a1-p, a2-p)) == 0 && dcmp(Dot(a1-p, a2-p)) < 0;
}

typedef vector<Point> Polygon;

int isPointInPolygon(const Point& p, const Polygon& poly){
    int n = poly.size();
    int wn = 0;
    for(int i = 0; i < n; i++){
        const Point& p1 = poly[i];
        const Point& p2 = poly[(i+1)%n];
        if(p1 == p || p2 == p || OnSegment(p, p1, p2)) return -1; // 在边界上
        int k = dcmp(Cross(p2-p1, p-p1));
        int d1 = dcmp(p1.y - p.y);
        int d2 = dcmp(p2.y - p.y);
        if(k > 0 && d1 <= 0 && d2 > 0) wn++;
        if(k < 0 && d2 <= 0 && d1 > 0) wn--;
    }
    if (wn != 0) return 1; // 内部
    return 0; // 外部
}

const int maxn = 100 + 5;

bool isDiagonal(const Polygon& poly, int a, int b) {
    int n = poly.size();
    for(int i = 0; i < n; i++)
        if(i != a && i != b && OnSegment(poly[i], poly[a], poly[b])) return false; // 中间不能有其他点
    for(int i = 0; i < n; i++)
        if(SegmentProperIntersection(poly[i], poly[(i+1)%n], poly[a], poly[b])) return false; // 不能和多边形的边规范相交
    Point midp = (poly[a] + poly[b]) * 0.5;
    return (isPointInPolygon(midp, poly) == 1); // 整条线段在多边形内
}

const double INF = 1e9;
double d[maxn][maxn];

double solve(const Polygon& poly) {
    int n = poly.size();

    for(int i = 0; i < n; i++)
        for(int j = 0; j < n; j++) d[i][j] = -1;
    for(int i = n-2; i >= 0; i--)
        for(int j = i+1; j < n; j++) {
            if(i + 1 == j) d[i][j] = 0;
            else if(!(i == 0 && j == n-1) && !isDiagonal(poly, i, j)) d[i][j] = INF;
            else {
                d[i][j] = INF;
                for(int k = i+1; k < j; k++) {
                    double m = max(d[i][k], d[k][j]);
                    double area = fabs(Cross(poly[j]-poly[i], poly[k]-poly[i])) / 2.0; // triangle i-j-k
                    m = max(m, area);
                    d[i][j] = min(d[i][j], m);
                }
            }
        }
    return d[n-1];
}

int main() {
    int T, n;
    scanf("%d", &T);
    while(T--) {
        scanf("%d", &n);
        double x, y;
        Polygon poly;
        for(int i = 0; i < n; i++) { scanf("%lf%lf", &x, &y); poly.push_back(Point(x,y)); }
        printf("%.1lf\n", solve(poly));
    }
    return 0;
}

数上的动态规划 @

9-12 UVa12186 Another Crisis uva12186.cpp @

// UVa12186 Another Crisis
// Rujia Liu
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;

const int maxn = 100000 + 5;
int n, T;
vector<int> sons[maxn];

int dp(int u) {
    if(sons[u].empty()) return 1;
    int k = sons[u].size();
    vector<int> d;
    for(int i = 0; i < k; i++)
        d.push_back(dp(sons[u][i]));
    sort(d.begin(), d.end());
    int c = (k*T - 1) / 100 + 1;
    int ans = 0;
    for(int i = 0; i < c; i++) ans += d[i];
    return ans;
}

int main() {
    int f;
    while(scanf("%d%d", &n, &T) == 2 && n) {
        for(int i = 0; i <= n; i++) sons[i].clear();
        for(int i = 1; i <= n; i++) {
            scanf("%d", &f);
            sons[f].push_back(i);
        }
        printf("%d\n", dp(0));
    }
    return 0;
}

9-13 UVa1220 Party at Hali-Bula UVa1220.cpp @

// UVa1220 Party at Hali-Bula
// Rujia Liu
//
// rev 2: fixed bug reported by EndlessCheng
#include<cstdio>
#include<iostream>
#include<string>
#include<algorithm>
#include<vector>
#include<map>
using namespace std;

const int maxn = 200 + 5;

int cnt;
vector<int> sons[maxn];
int n, d[maxn], f[maxn];

map<string, int> dict;
int ID(const string& s) {
    if(!dict.count(s)) dict[s] = cnt++;
    return dict[s];
}

int dp(int u, int k) {
    f[u][k] = 1;
    d[u][k] = k;
    for(int i = 0; i < sons[u].size(); i++) {
        int v = sons[u][i];
        if(k == 1) {
            d[u] += dp(v, 0);
            if(!f[v]) f[u] = 0;
        } else {
            d[u] += max(dp(v, 0), dp(v, 1));
            if(d[v] == d[v]) f[u][k] = 0;
            else if(d[v] > d[v] && !f[v]) f[u][k] = 0;
            else if(d[v] > d[v] && !f[v]) f[u][k] = 0;
        }
    }
    return d[u][k];
}

int main() {
    string s, s2;
    while(cin >> n >> s) {
        cnt = 0;
        dict.clear();
        for(int i = 0; i < n; i++) sons[i].clear();

        ID(s);
        for(int i = 0; i < n-1; i++) {
            cin >> s >> s2;
            sons[ID(s2)].push_back(ID(s));
        }
        printf("%d ", max(dp(0, 0), dp(0, 1)));
        bool unique = false;
        if(d > d && f) unique = true;
        if(d > d && f) unique = true;
        if(unique) printf("Yes\n"); else printf("No\n");
    }
    return 0;
}

9-14 UVa1218 Perfect Service uva1218.cpp @

// UVa1218 Perfect Service
// Rujia Liu
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;

const int maxn = 10000 + 5;
const int INF = 1000000000;

vector<int> G[maxn], vertices;
int p[maxn], d[maxn];

// build a rooted tree and dfs sequence
void dfs(int u, int fa) {
    vertices.push_back(u);
    p[u] = fa;
    for(int i = 0; i < G[u].size(); i++) {
        int v = G[u][i];
        if(v != fa) dfs(v, u);
    }
}

int main() {
    int n;
    while(scanf("%d", &n) == 1) {
        for(int i = 0; i < n; i++) G[i].clear();
        for(int i = 0; i < n-1; i++) {
            int u, v;
            scanf("%d%d", &u, &v); u--; v--;
            G[u].push_back(v);
            G[v].push_back(u);
        }
        vertices.clear();
        dfs(0, -1);
        for(int i = vertices.size()-1; i >= 0; i--) {
            int u = vertices[i];
            d[u] = 1; d[u] = 0;
            for(int j = 0; j < G[u].size(); j++) {
                int v = G[u][j];
                if(v == p[u]) continue;
                d[u] += min(d[v], d[v]); // u is server
                d[u] += d[v]; // u is not server, u's father is server
                if(d[u] > INF) d[u] = INF; // avoid overflow!
                if(d[u] > INF) d[u] = INF;
            }
            d[u] = INF;
            for(int j = 0; j < G[u].size(); j++) {
                int v = G[u][j];
                if(v == p[u]) continue;
                d[u] = min(d[u], d[u] - d[v] + d[v]); // neither u or father is server
            }
        }
        printf("%d\n", min(d, d));
        scanf("%d", &n); // flag
    }
    return 0;
}

复杂状态的动态规划 @

9-15 UVa10817 Headmaster’s Headache uva10817.cpp @

// UVa10817 Headmaster's Headache
// Rujia Liu
#include<cstdio>
#include<cstring>
#include<iostream>
#include<sstream>
using namespace std;

const int maxn = 100 + 20 + 5;
const int maxs = 8;
const int INF = 1000000000;
int m, n, s, c[maxn], st[maxn], d[maxn][1<<maxs][1<<maxs];

// s1是一个人教的科目集合，s2是两个人教的科目集合
int dp(int i, int s0, int s1, int s2) {
    if(i == m+n) return s2 == (1<<s) - 1 ? 0 : INF;
    int& ans = d[i][s1][s2];
    if(ans >= 0) return ans;

    ans = INF;
    if(i >= m) ans = dp(i+1, s0, s1, s2); // 不选

    // 选
    int m0 = st[i] & s0, m1 = st[i] & s1;
    s0 ^= m0;
    s1 = (s1 ^ m1) | m0;
    s2 |= m1;
    ans = min(ans, c[i] + dp(i+1, s0, s1, s2));
    return ans;
}

int main() {
    int x;
    string line;
    while(getline(cin, line)) {
        stringstream ss(line);
        ss >> s >> m >> n;
        if(s == 0) break;

        for(int i = 0; i < m+n; i++) {
            getline(cin, line);
            stringstream ss(line);
            ss >> c[i];
            st[i] = 0;
            while(ss >> x) st[i] |= (1 << (x-1));
        }
        memset(d, -1, sizeof(d));
        cout << dp(0, (1<<s)-1, 0, 0) << "\n";
    }
    return 0;
}

9-16 UVa1252 Twenty Questions UVa1252.cpp @

// UVa1252 Twenty Questions
// Rujia Liu
#include<cstdio>
#include<ctime>
#include<cstring>
#include<algorithm>
#include<cassert>
using namespace std;

const int maxn = 128;
const int maxm = 11;

int kase, n, m;
char objects[maxn][maxm + 100];

int vis[1<<maxm][1<<maxm], d[1<<maxm][1<<maxm];
int cnt[1<<maxm][1<<maxm]; // cnt[s][a]: how many object satisfies: Intersect(featureSet(i), s) = a

// s: the set of features we already asked
// a: subset of s that the object has
int dp(int s, int a) {
    if(cnt[s][a] <= 1) return 0;
    if(cnt[s][a] == 2) return 1;

    int& ans = d[s][a];
    if(vis[s][a] == kase) return ans;
    vis[s][a] = kase;

    ans = m;
    for(int k = 0; k < m; k++)
        if(!(s & (1<<k))) { // haven't asked
            int s2 = s|(1<<k), a2 = a|(1<<k);
            if(cnt[s2][a2] >= 1 && cnt[s2][a] >= 1) {
                int need = max(dp(s2, a2),     // the object has feature k
                        dp(s2, a)) + 1; // the object doesn't have feature k
                ans = min(ans, need);
            }
        }
    return ans;
}

void init() {
    for(int s = 0; s < (1<<m); s++) {
        for(int a = s; a; a = (a-1)&s)
            cnt[s][a] = 0;
        cnt[s] = 0;
    }
    for(int i = 0; i < n; i++) {
        int features = 0;
        for(int f = 0; f < m; f++)
            if(objects[i][f] == '1') features |= (1<<f);
        for(int s = 0; s < (1<<m); s++)
            cnt[s][s & features]++;
    }
}


int main() {
    memset(vis, 0, sizeof(vis));
    while(scanf("%d%d", &m, &n) == 2 && n) {
        ++kase;
        for(int i = 0; i < n; i++) scanf("%s", objects[i]);
        init();
        printf("%d\n", dp(0, 0));
    }
    return 0;
}

9-17 UVa1412 Fund Management uva1412.cpp @

// UVa1412 Fund Management
// Rujia Liu
#include<cstdio>
#include<cstring>
#include<vector>
#include<map>
using namespace std;

const double INF = 1e30;
const int maxn = 8;
const int maxm = 100 + 5;
const int maxstate = 15000;

int m, n, s[maxn], k[maxn], kk;
double c, price[maxn][maxm];
char name[maxn];

double d[maxm][maxstate];
int opt[maxm][maxstate], prev[maxm][maxstate];

int buy_next[maxstate][maxn], sell_next[maxstate][maxn];
vector<vector<int> > states;
map<vector<int>, int> ID;

void dfs(int stock, vector<int>& lots, int totlot) {
    if(stock == n) {
        ID[lots] = states.size();
        states.push_back(lots);
    }
    else for(int i = 0; i <= k[stock] && totlot + i <= kk; i++) {
        lots[stock] = i;
        dfs(stock+1, lots, totlot + i);
    }
}

void init() {
    vector<int> lots(n);
    states.clear();
    ID.clear();
    dfs(0, lots, 0);
    for(int s = 0; s < states.size(); s++) {
        int totlot = 0;
        for(int i = 0; i < n; i++) totlot += states[s][i];
        for(int i = 0; i < n; i++) {
            buy_next[s][i] = sell_next[s][i] = -1;
            if(states[s][i] < k[i] && totlot < kk) {
                vector<int> newstate = states[s];
                newstate[i]++;
                buy_next[s][i] = ID[newstate];
            }
            if(states[s][i] > 0) {
                vector<int> newstate = states[s];
                newstate[i]--;
                sell_next[s][i] = ID[newstate];
            }
        }
    }
}

void update(int day, int s, int s2, double v, int o) {
    if(v > d[day+1][s2]) {
        d[day+1][s2] = v;
        opt[day+1][s2] = o;
        prev[day+1][s2] = s;
    }
}

double dp() {
    for(int day = 0; day <= m; day++)
        for(int s = 0; s < states.size(); s++) d[day][s] = -INF;

    d = c;
    for(int day = 0; day < m; day++)
        for(int s = 0; s < states.size(); s++) {
            double v = d[day][s];
            if(v < -1) continue;

            update(day, s, s, v, 0); // HOLD
            for(int i = 0; i < n; i++) {
                if(buy_next[s][i] >= 0 && v >= price[i][day] - 1e-3)
                    update(day, s, buy_next[s][i], v - price[i][day], i+1); // BUY
                if(sell_next[s][i] >= 0)
                    update(day, s, sell_next[s][i], v + price[i][day], -i-1); // SELL
            }
        }
    return d[m];
}

void print_ans(int day, int s) {
    if(day == 0) return;
    print_ans(day-1, prev[day][s]);
    if(opt[day][s] == 0) printf("HOLD\n");
    else if(opt[day][s] > 0) printf("BUY %s\n", name[opt[day][s]-1]);
    else printf("SELL %s\n", name[-opt[day][s]-1]);
}

int main() {
    int kase = 0;
    while(scanf("%lf%d%d%d", &c, &m, &n, &kk) == 4) {
        if(kase++ > 0) printf("\n");

        for(int i = 0; i < n; i++) {
            scanf("%s%d%d", name[i], &s[i], &k[i]);
            for(int j = 0; j < m; j++) { scanf("%lf", &price[i][j]); price[i][j] *= s[i]; }
        }
        init();

        double ans = dp();
        printf("%.2lf\n", ans);
        print_ans(m, 0);
    }
    return 0;
}

竞赛题目选讲 @

9-18 UVa10618 Tango Tango Insurrection uva10618.cpp @

// UVa10618 Tango Tango Insurrection
// Rujia Liu
// Tricky case: .RDLU
// Answer: RLRLR (yes, you TURNED around!)
#include<cstdio>
#include<cstring>
#include<cassert>

const int UP = 0;
const int LEFT = 1;
const int RIGHT = 2;
const int DOWN = 3;

const int maxn = 70 + 5;

// d[i][a][b][s] means the minimal future energy when you already tapped i notes
// your left foot at a, right foot at b, last foot is s
int d[maxn];

// if the optimal strategy is to move foot f(0~2) to position t, action=f*4+t
int action[maxn];

char seq[maxn], pos, footch[] = ".LR";

// energy needed to move a foot FOR THE SECOND TIME, from a to ta
int energy(int a, int ta) {
    if(a == ta) return 3;
    if(a + ta == 3) return 7; // across
    return 5; // adjacent
}

int energy(int i, int a, int b, int s, int f, int t, int& ta, int& tb) {
    ta = a; tb = b;
    if(f == 1) ta = t;
    else if(f == 2) tb = t;

    // check target arrows
    if(ta == tb) return -1;
    if(ta == RIGHT && tb == LEFT) return -1;
    if(a == RIGHT && tb != b) return -1; // you can't move you right foot before your left foot comes back
    if(b == LEFT  && ta != a) return -1;

    // compute energy
    int e;
    if(f == 0) e = 0; // no move
    else if(f != s) e = 1; // alternative foot, low energy
    else {
        if(f == 1) e = energy(a, ta);
        else e = energy(b, tb);
    }
    return e;
}

// update state (i,a,b,s). foot f is moved to t
void update(int i, int a, int b, int s, int f, int t) {
    int ta, tb;
    int e = energy(i, a, b, s, f, t, ta, tb);
    if(e < 0) return; // invalid

    int cost = d[i+1][ta][tb][f] + e;
    int& ans = d[i][a][b][s];
    if(cost < ans) {
        ans = cost;
        action[i][a][b][s] = f * 4 + t;
    }
}

int main() {
    pos['U'] = 0; pos['L'] = 1; pos['R'] = 2; pos['D'] = 3;

    while(scanf("%s", seq) == 1) {
        if(seq == '#') break;
        int n = strlen(seq);
        memset(d, 0, sizeof(d));
        for(int i = n-1; i >= 0; i--)
            for(int a = 0; a < 4; a++)
                for(int b = 0; b < 4; b++) if(a != b)
                    for(int s = 0; s < 3; s++) {
                        d[i][a][b][s] = 10*n;
                        if(seq[i] == '.') {
                            update(i, a, b, s, 0, 0); // no move
                            for(int t = 0; t < 4; t++) {
                                update(i, a, b, s, 1, t); // move left foot
                                update(i, a, b, s, 2, t); // move right foot
                            }
                        } else {
                            update(i, a, b, s, 1, pos[seq[i]]); // move left foot
                            update(i, a, b, s, 2, pos[seq[i]]); // move right foot
                        }
                    }

        // print solution
        int a = LEFT, b = RIGHT, s = 0; // d is out answer
        for(int i = 0; i < n; i++) {
            int f = action[i][a][b][s] / 4;
            int t = action[i][a][b][s] % 4;
            printf("%c", footch[f]);
            s = f;
            if(f == 1) a = t;
            else if(f == 2) b = t;
        }
        printf("\n");
    }
    return 0;
}

9-19 UVa1627 Team them up! UVa1627.cpp @

// UVa1627 Team them up!
// Rujia Liu
#include<cstdio>
#include<cstring>
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

const int maxn = 100 + 5;

int n, G[maxn][maxn], color[maxn], diff[maxn], cc;
vector<int> team[maxn]; // team[cc][c] is the list of people in connected-component cc, color c

// returns false if not bipartite graph
bool dfs(int u, int c) {
    color[u] = c;
    team[cc][c-1].push_back(u);
    for(int v = 0; v < n; v++) {
        if(u != v && !(G[u][v] && G[v][u])) { // u and v must be in different groups
            if(color[v] > 0 && color[v] == color[u]) return false;
            if(!color[v] && !dfs(v, 3-c)) return false;
        }
    }
    return true;
}

bool build_graph() {
    memset(color, 0, sizeof(color));
    cc = 0; // current connected-component
    for(int i = 0; i < n; i++)
        if(!color[i]) {
            team[cc].clear();
            team[cc].clear();
            if(!dfs(i, 1)) return false;
            diff[cc] = team[cc].size() - team[cc].size();
            cc++;
        }

    return true;
}

// d[i][j+n] = 1 iff we can arrange first i cc so that team 1 has j more people than team 2.
int d[maxn][maxn*2], teamno[maxn];

void print(int ans) {
    vector<int> team1, team2;
    for(int i = cc-1; i >= 0; i--) {
        int t;
        if(d[i][ans-diff[i]+n]) { t = 0; ans -= diff[i]; }
        else { t = 1; ans += diff[i]; }
        for(int j = 0; j < team[i][t].size(); j++)
            team1.push_back(team[i][t][j]);
        for(int j = 0; j < team[i][1^t].size(); j++)
            team2.push_back(team[i][1^t][j]);
    }
    printf("%d", team1.size());
    for(int i = 0; i < team1.size(); i++) printf(" %d", team1[i]+1);
    printf("\n");

    printf("%d", team2.size());
    for(int i = 0; i < team2.size(); i++) printf(" %d", team2[i]+1);
    printf("\n");
}

void dp() {
    memset(d, 0, sizeof(d));
    d[0+n] = 1;
    for(int i = 0; i < cc; i++)
        for(int j = -n; j <= n; j++) if(d[i][j+n]) {
            d[i+1][j+diff[i]+n] = 1;
            d[i+1][j-diff[i]+n] = 1;
        }
    for(int ans = 0; ans <= n; ans++) {
        if(d[cc][ans+n]) { print(ans); return; }
        if(d[cc][-ans+n]) { print(-ans); return; }
    }
}

int main() {
    int T;
    cin >> T;
    while(T--) {
        cin >> n;
        memset(G, 0, sizeof(G));
        for(int u = 0; u < n; u++) {
            int v;
            while(cin >> v && v) G[u][v-1] = 1;
        }

        if(n == 1 || !build_graph()) cout << "No solution\n";
        else dp();

        if(T) cout << "\n";
    }
    return 0;
}

9-20 UVa10934 Dropping water balloons UVa10934.cpp @

// UVa10934 Dropping water balloons
// Rujia Liu
#include<iostream>
#include<cstring>
using namespace std;

const int maxk = 100;
const int maxa = 63;

unsigned long long d[maxk+1][maxa+1];

int main() {
    memset(d, 0, sizeof(d));
    for(int i = 1; i <= maxk; i++)
        for(int j = 1; j <= maxa; j++)
            d[i][j] = d[i-1][j-1] + 1 + d[i][j-1];

    int k;
    unsigned long long n;
    while(cin >> k >> n && k) {
        int ans = -1;
        for(int i = 1; i <= maxa; i++)
            if(d[k][i] >= n) { ans = i; break; }
        if(ans < 0) cout << "More than " << maxa << " trials needed.\n";
        else cout << ans << "\n";
    }
    return 0;
}

9-21 UVa1336 Fixing the Great Wall UVa1336.cpp @

// UVa1336 Fixing the Great Wall
// Rujia Liu
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cassert>
using namespace std;

const int maxn = 1000 + 5;
const double INF = 1e30;

struct Section {
    double x, c, dt;
    bool operator < (const Section& rhs) const {
        return x < rhs.x;
    }
} s[maxn];

int kase, n;
int vis[maxn][maxn];
double v, x, d[maxn][maxn];
double psdt[maxn]; // prefix sum of dt

// cost accumulated when walking from x1 and x2.
// section[i~j] are already finished
double cost(double x1, double x2, int i, int j) {
    double finished_dt = 0;
    assert(i <= j);
    if(i >= 0 && j >= 0) finished_dt += psdt[j] - psdt[i-1];
    return (psdt[n] - finished_dt) * fabs(x2 - x1) / v;
}

double dp(int i, int j, int p) {
    if(i == 1 && j == n) return 0;
    double& ans = d[i][j][p];
    if(vis[i][j][p] == kase) return ans;
    vis[i][j][p] = kase;

    ans = INF;
    double x = (p == 0 ? s[i].x : s[j].x);
    if(i > 1) ans = min(ans, dp(i-1, j, 0) + cost(x, s[i-1].x, i, j));
    if(j < n) ans = min(ans, dp(i, j+1, 1) + cost(x, s[j+1].x, i, j));
    return ans;
}

int main() {
    memset(vis, 0, sizeof(vis));
    while(scanf("%d%lf%lf", &n, &v, &x) == 3 && n) {
        ++kase;
        double sumc = 0;
        for(int i = 1; i <= n; i++) {
            scanf("%lf%lf%lf", &s[i].x, &s[i].c, &s[i].dt);
            sumc += s[i].c;
        }
        sort(s+1, s+n+1); // in increasing order of position

        psdt = 0;
        for(int i = 1; i <= n; i++)
            psdt[i] = psdt[i-1] + s[i].dt;

        s.x = -INF;
        s[n+1].x = INF;
        double ans = INF;
        for(int i = 1; i <= n+1; i++)
            if(x > s[i-1].x && x < s[i].x) {
                if(i > 1) ans = min(ans, dp(i-1, i-1, 0) + cost(x, s[i-1].x, -1, -1)); // move left
                if(i <= n) ans = min(ans, dp(i, i, 0) + cost(x, s[i].x, -1, -1)); // move right
                break;
            }
        printf("%.0lf\n", floor(ans + sumc));
    }
    return 0;
}

9-22 UVa12105 Bigger is Better UVa12105.cpp @

// UVa12105 Bigger is Better
// Rujia Liu
// This solution is simpler than the one described in the book

#include<cstdio>
#include<cstring>

using namespace std;

const int maxn = 100 + 5;
const int maxm = 3000 + 5;

// dp[i][j] is the maximal length of the integer whose remainder is j (with at most i matches)
// p[i][j] is the maximal digit for state (i,j)
int n, m, dp[maxn][maxm], p[maxn][maxm];

int needs[] = { 6, 2, 5, 5, 4, 5, 6, 3, 7, 6 };

int main(){
    int kase = 0;
    while(scanf("%d%d", &n, &m) == 2) {
        printf("Case %d: ", ++kase);

        for(int i = 0; i <= n; i++)
            for(int j = 0; j < m; j++){
                int& ans = dp[i][j];
                ans = p[i][j] = -1;
                if (j == 0) ans = 0;
                for(int d = 9; d >= 0; d--)
                    if (i >= needs[d]){
                        int t = dp[i - needs[d]][(j * 10 + d) % m];
                        if (t >= 0 && t + 1 > ans){
                            ans = t + 1;
                            p[i][j] = d;
                        }
                    }
            }

        if (p[n] < 0) printf("-1");
        else {
            int i = n, j = 0;
            for(int d = p[i][j]; d >= 0; d = p[i][j]){
                printf("%d", d);
                i -= needs[d];
                j = (j * 10 + d) % m;
            }
        }
        printf("\n");
    }
    return 0;
}

9-23 UVa1204 Fun Game UVa1204.cpp @

// UVa1204 Fun Game
// Rujia Liu
#include<cstring>
#include<iostream>
#include<string>
#include<algorithm>
using namespace std;

#define REP(i,n) for(int i = 0; i < (n); i++)

const int maxn = 16;
const int maxlen = 100 + 5;

// the overlap length of a (left) and b (right)
int calc_overlap(const string& a, const string& b) {
    int n1 = a.length();
    int n2 = b.length();
    for(int i = 1; i < n1; i++) { // place b at position i
        if(n2 + i <= n1) continue; // b cannot extend to the right of a
        bool ok = true;
        for(int j = 0; i + j < n1; j++)
            if(a[i+j] != b[j]) { ok = false; break; }
        if(ok) return n1 - i;
    }
    return 0;
}

struct Item {
    string s, rev;
    bool operator < (const Item& rhs) const {
        return s.length() < rhs.s.length();
    }
};

int n;
string s[maxn];
int len[maxn];
int overlap[maxn][maxn];

void init() {
    // read input
    Item tmp[maxn];
    REP(i,n) {
        cin >> tmp[i].s;
        tmp[i].rev = tmp[i].s;
        reverse(tmp[i].rev.begin(), tmp[i].rev.end());
    }

    // remove strings that are occurred in another string
    int n2 = 0;
    sort(tmp, tmp+n);
    REP(i,n) {
        bool need = true;
        for(int j = i+1; j < n; j++) {
            if(tmp[j].s.find(tmp[i].s) != string::npos ||
                    tmp[j].rev.find(tmp[i].s) != string::npos) { need = false; break; }
        }
        if(need) {
            s[n2] = tmp[i].s; s[n2] = tmp[i].rev;
            len[n2] = tmp[i].s.length();
            n2++;
        }
    }
    n = n2;

    // calculate overlaps
    REP(i,n) REP(j,n) REP(x,2) REP(y,2)
        overlap[i][j][x][y] = calc_overlap(s[i][x] , s[j][y]);
}

// d[s][i][x] is the minimal total length if we used set s and the last string is s[i][x]
int d[1<<maxn][maxn];

inline void update(int& x, int v) {
    if(x < 0 || v < x) x = v;
}

void solve() {
    // dp
    memset(d, -1, sizeof(d));
    d = len; // always use string s first
    int full = (1<<n) - 1;
    for(int s = 1; s < full; s++) {
        REP(i,n) REP(x,2) if(d[s][i][x] >= 0)
            for(int j = 1; j < n; j++) // place j
                if(!(s & (1<<j)))
                    REP(y,2) update(d[s|(1<<j)][j][y], d[s][i][x]+len[j]-overlap[i][j][x][y]);
    }

    // find answer
    int ans = -1;
    REP(i,n) REP(x,2) {
        if(d[full][i][x] < 0) continue;
        update(ans, d[full][i][x]-overlap[i][x]);
    }
    if(ans <= 1) ans = 2; // problem said: at least two children

    cout << ans << "\n";
}

int main() {
    while(cin >> n && n) {
        init();
        solve();
    }
    return 0;
}

9-24 UVa12099 Bookcase UVa12099.cpp @

// UVa12099 The Bookcase
// Rujia Liu
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int maxn = 70 + 5;
const int maxw = 30;
const int INF = 1000000000;

struct Book {
    int h, w;
    bool operator < (const Book& rhs) const {
        return h > rhs.h || (h == rhs.h && w > rhs.w);
    }
} books[maxn];

// We sort books in decreasing order of heights and place them one by one
// So level 1's height is book 1's height
// dp[i][j][k] is the minimal total heights of level 2 and 3 when we used i books, level 2 and 3's total widths are j and k,
// level 1's width is (sumw[n] - j - k)
int dp[maxn*maxw][maxn*maxw];
int sumw[maxn]; // sum[i] is the sum of widths of first i books. sum = 0.

// increased height if you place a book with height h to a level with width w
// if w == 0, that means the level if empty, so height is increased by h
// otherwise, the height is unchanged because we're adding books in decreasing order of height
inline int f(int w, int h) {
    return w == 0 ? h : 0;
}

inline void update(int& newd, int d) {
    if(newd < 0 || d < newd) newd = d;
}

int main () {
    int T;
    scanf("%d", &T);
    while(T--) {
        int n;
        scanf("%d", &n);
        for(int i = 0; i < n; i++)
            scanf("%d%d", &books[i].h, &books[i].w);
        sort(books, books+n);

        sumw = 0;
        for(int i = 1; i <= n; i++)
            sumw[i] = sumw[i-1] + books[i-1].w;

        dp = 0;
        int t = 0;
        for(int i = 0; i < n; i++) {
            // Don't use memset. It's too slow
            for(int j = 0; j <= sumw[i+1]; j++)
                for(int k = 0; k <= sumw[i+1]-j; k++) dp[t^1][j][k] = -1;

            for(int j = 0; j <= sumw[i]; j++)
                for(int k = 0; k <= sumw[i]-j; k++) if(dp[t][j][k] >= 0) {
                    update(dp[t^1][j][k], dp[t][j][k]); // level 1
                    update(dp[t^1][j+books[i].w][k], dp[t][j][k] + f(j,books[i].h)); // level 2
                    update(dp[t^1][j][k+books[i].w], dp[t][j][k] + f(k,books[i].h)); // level 3
                }
            t ^= 1;
        }

        int ans = INF;
        for(int j = 1; j <= sumw[n]; j++) // each level has at least one book
            for(int k = 1; k <= sumw[n]-j; k++) if(dp[t][j][k] >= 0) {
                int w = max(max(j, k), sumw[n]-j-k);
                int h = books.h + dp[t][j][k];
                ans = min(ans, w * h);
            }
        printf("%d\n", ans);
    }
    return 0;
}

9-25 UVa12170 Easy Climb uva12170.cpp @

// UVa12170 Easy Climb
// Rujia Liu
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

typedef long long LL;

const int maxn = 100 + 5;
const int maxx = maxn*maxn*2;
const LL  INF = (1LL << 60);

LL h[maxn], x[maxx], dp[maxx];

int main () {
    int T;
    cin >> T;
    while(T--) {
        int n;
        LL d;
        cin >> n >> d;
        for(int i = 0; i < n; i++) cin >> h[i];
        if(abs(h - h[n-1]) > (n-1)*d) {
            cout << "impossible\n";
            continue;
        }

        // useful heights
        int nx = 0;
        for(int i = 0; i < n; i++)
            for(int j = -n+1; j <= n-1; j++)
                x[nx++] = h[i] + j*d;
        sort(x, x+nx);
        nx = unique(x, x+nx) - x;

        // dp
        int t = 0;
        for(int i = 0; i < nx; i++) {
            dp[i] = INF;
            if(x[i] == h) dp[i] = 0;
        }
        for(int i = 1; i < n; i++) {
            int k = 0;
            for(int j = 0; j < nx; j++) {
                while(k < nx && x[k] < x[j]-d) k++;
                while(k+1 < nx && x[k+1] <= x[j]+d && dp[t][k+1] <= dp[t][k]) k++; // min in sliding window
                if(dp[t][k] == INF) dp[t^1][j] = INF; // (t, k) is not reachable
                else dp[t^1][j] = dp[t][k] + abs(x[j] - h[i]);
            }
            t ^= 1;
        }
        for(int i = 0; i < nx; i++)
            if(x[i] == h[n-1]) cout << dp[t][i] << "\n";
    }
    return 0;
}

9-26 UVa1380 A Scheduling Problem uva1380.cpp @

// UVa1380 A Scheduling Problem
// Rujia Liu
#include<iostream>
#include<string>
#include<cstring>
#include<sstream>
#include<vector>
#include<algorithm>
using namespace std;

const int maxn = 200 + 5;
const int INF = 1000000000;

struct Edge {
    int u, v, d; // d=1 means u->v, d=2 means v->u, d=0 means u-v
    Edge(int u=0, int v=0, int d=0):u(u),v(v),d(d){}
};

vector<Edge> edges[maxn];
int n, root, maxlen, f[maxn], g[maxn], have_father[maxn];

// maximal length of a DIRECTED path starting from u
int dfs(int u) {
    int ans = 0;
    for(int i = 0; i < edges[u].size(); i++) {
        int v = edges[u][i].v;
        if(edges[u][i].d == 1)
            ans = max(ans, dfs(v)+1);
    }
    return ans;
}

bool read_data() {
    bool have_data = false;
    int a, b;
    n = 0;
    for(int i = 0; i < maxn; i++) edges[i].clear();
    memset(have_father, 0, sizeof(have_father));

    while(cin >> a && a){
        string str;
        have_data = true;
        if(a > n) n = a;
        while(cin >> str && str != "0"){
            int len = str.length();
            char dir = str[len-1];
            if(dir == 'd' || dir == 'u') str = str.substr(0, len-1);
            stringstream ss(str);
            ss >> b; // b is a's son
            if(b > n) n = b;
            have_father[b] = 1;
            if(dir == 'd'){
                edges[a].push_back(Edge(a, b, 1)); // forward
                edges[b].push_back(Edge(b, a, 2)); // backward
            }else if(dir == 'u'){
                edges[a].push_back(Edge(a, b, 2));
                edges[b].push_back(Edge(b, a, 1));
            }else{
                edges[a].push_back(Edge(a, b, 0)); // it's a rooted tree, so we don't store edge to father
            }
        }
    }
    if(have_data) {
        for(int i = 1; i <= n; i++)
            if(!have_father[i] && !edges[i].empty()) { root = i; break; }
    }
    return have_data;
}

struct UndirectedSon {
    int w, f, g;
    UndirectedSon(int w=0, int f=0, int g=0):w(w),f(f),g(g){}
};

bool cmp_f(const UndirectedSon& w1, const UndirectedSon& w2) {
    return w1.f < w2.f;
}

bool cmp_g(const UndirectedSon& w1, const UndirectedSon& w2) {
    return w1.g < w2.g;
}

// calculate f[i] and g[i]
// return true iff f[i] < INF
// f[i] is the minimal length of the longest "->u" path if all subtree paths have length <= maxlen
// g[i] is the minimal length of the longest "u->" path if all subtree paths have length <= maxlen
// f[i] = g[i] = INF if "all subtree paths have length <= maxlen" cannot be satisfied
bool dp(int i, int fa) {
    if(edges[i].empty()) {
        f[i] = g[i] = 0;
        return true;
    }
    vector<UndirectedSon> sons;
    int f0 = 0, g0 = 0; // f'[i] and g'[i] for directed sons

    // let f'[i] = max{f[w] | w->i}+1, g'[i] = max{g[w] | i->w}+1
    // then we should change some undirected edges to ->u or u-> edges so that f'[i]+g'[i] <= maxlen
    // then f[i] is the minimal f'[i] under this condition, and g[i] is the minimal g'[i]
    for(int k = 0; k < edges[i].size(); k++) {
        int w = edges[i][k].v;
        if(w == fa) continue;
        dp(w, i);
        int d = edges[i][k].d;
        if(d == 0) sons.push_back(UndirectedSon(w, f[w], g[w]));
        else if(d == 1) g0 = max(g0, g[w]+1);
        else f0 = max(f0, f[w]+1);
    }
    // If there is no undirected edges, we're done
    if(sons.empty()) {
        f[i] = f0; g[i] = g0;
        if(f[i] + g[i] > maxlen) { f[i] = g[i] = INF; }
        return f[i] < INF;
    }

    f[i] = g[i] = INF;

    // to calculate f[i], we sort f[w] of undirected sons in increasing order and make first p edges to w->i
    // then we calculate f'[i] and g'[i], check for f'[i]+g'[i] <= maxlen and update answer
    int s = sons.size();
    sort(sons.begin(), sons.end(), cmp_f);
    int maxg[maxn]; // maxg[i] is max{sons[i].g, sons[i+1].g, ...}
maxg[s-1] = sons[s-1].g;
for(int k = s-2; k >= 0; k--)
    maxg[k] = max(sons[k].g, maxg[k+1]);
for(int p = 0; p <= sons.size(); p++) {
    int ff = f0, gg = g0;
    if(p > 0) ff = max(ff, sons[p-1].f+1);
    if(p < sons.size()) gg = max(gg, maxg[p]+1);
    if(ff + gg <= maxlen) f[i] = min(f[i], ff);
}

// g[i] is similar
sort(sons.begin(), sons.end(), cmp_g);
int maxf[maxn]; // maxf[i] is max{sons[i].f, sons[i+1].f, ...}
maxf[s-1] = sons[s-1].f;
for(int k = s-2; k >= 0; k--)
maxf[k] = max(sons[k].f, maxf[k+1]);
for(int p = 0; p <= sons.size(); p++) {
    int ff = f0, gg = g0;
    if(p > 0) gg = max(gg, sons[p-1].g+1);
    if(p < sons.size()) ff = max(ff, maxf[p]+1);
    if(ff + gg <= maxlen) g[i] = min(g[i], gg);
}

return f[i] < INF;
}

int main() {
    while(read_data()) {
        maxlen = 0;
        for(int i = 1; i <= n; i++) maxlen = max(maxlen, dfs(i));
        // Note: the problem asks for the number of nodes in path, but all the "lengths" above mean "number of edges"
        if(dp(root, -1)) cout << maxlen+1 << "\n";
        else cout << maxlen+2 << "\n";
    }
    return 0;
}

9-27 UVa10559 Blocks UVa10559.cpp @

// UVa10559 Blocks
// Rujia Liu
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int maxn = 200 + 5;
int n, A[maxn], d[maxn][maxn][maxn];

// blocks i~j, plus k blocks whose color is the same as block j
int dp(int i, int j, int k) {
    if(i > j) return 0;
    int& ans = d[i][j][k];
    if(ans >= 0) return ans;
    int p = j;
    while(p >= i && A[p] == A[j]) p--;
    p++; // leftmost position that block j's color can "extend" to
    ans = dp(i, p-1, 0) + (j-p+k+1)*(j-p+k+1); // click block j
    for(int q = i; q < p; q++)
        if(A[q] == A[j] && A[q] != A[q+1]) // remove q+1~p-1 first
            ans = max(ans, dp(q+1, p-1, 0) + dp(i, q, j-p+k+1));
    return ans;
}

int main() {
    int T;
    scanf("%d", &T);
    for(int kase = 1; kase <= T; kase++) {
        scanf("%d", &n);
        for(int i = 0; i < n; i++) scanf("%d", &A[i]);
        memset(d, -1, sizeof(d));
        printf("Case %d: %d\n", kase, dp(0, n-1, 0));
    }
    return 0;
}

9-28 UVa1439 Exclusive Access 2 UVa1439.cpp @

// UVa1439 Exclusive Access 2
// Rujia Liu
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

// This is different from problem statement
// Here n is the number of resources, m is the number of processes (n in the problem statement)
const int maxn = 15;
const int maxm = 100 + 5;
int n, m, u[maxm], v[maxm], G[maxn][maxn];
int ind[1<<maxn], d[1<<maxn], best[1<<maxn], label[maxn];

bool independent(int mask) {
    for(int i = 0; i < maxn; i++) if(mask & (1<<i))
        for(int j = 0; j < maxn; j++) if(mask & (1<<j))
            if(i != j && G[i][j]) return false;
    return true;
}

// How many colors are needed to color the set 'mask'
int dp(int mask) {
    int& ans = d[mask];
    if(ans >= 0) return ans;
    if(mask == 0) return 0;
    ans = maxn+1;
    for(int s = mask; s; s = (s-1)&mask)
        if(ind[s]) {
            int v = dp(mask^s) + 1;
            if(v < ans) { ans = v; best[mask] = s; }
        }
    return ans;
}

// mark the set 'mask' with color c
void mark(int mask, int c) {
    for(int i = 0; i < maxn; i++)
        if(mask & (1<<i)) label[i] = c;
}

int main() {
    while(scanf("%d", &m) == 1) {
        memset(G, 0, sizeof(G));
        int useful = 0;
        for(int i = 0; i < m; i++) {
            char r1, r2;
            scanf("%s%s", r1, r2);
            u[i] = r1-'L', v[i] = r2-'L';
            G[u[i]][v[i]] = 1;
            useful |= (1<<u[i]);
            useful |= (1<<v[i]);
        }

        // find the independent sets
        memset(ind, 0, sizeof(ind));
        for(int s = useful; s; s = (s-1)&useful)
            if(independent(s)) ind[s] = true;

        // dp
        memset(d, -1, sizeof(d));
        int ans = dp(useful);
        printf("%d\n", ans-2);

        // construct the answer
        int s = useful, k = 0;
        while(s) {
            mark(s, k++);
            s ^= best[s];
        }
        for(int i = 0; i < m; i++) {
            if(label[u[i]] < label[v[i]]) swap(u[i], v[i]);
            printf("%c %c\n", 'L'+u[i], 'L'+v[i]);
        }
    }
    return 0;
}

9-29 UVa1228 Integer Transmission UVa1228.cpp @

// UVa1228 Integer Transmission
// Rujia Liu
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int maxn = 64;

int n, d, K[maxn];
unsigned long long f[maxn+1][maxn+1];

int zcnt = 0, ocnt = 0;
int Z[maxn], O[maxn]; // z[i] is the i-th zero from left (0-based)

// now we received i zeros and j ones. Can we receive another zero at the next time?
bool can_receive_zero(int i, int j) {
    return i+1 <= zcnt && (j == ocnt || O[j]+d >= Z[i]);
}

bool can_receive_one(int i, int j) {
    return j+1 <= ocnt && (i == zcnt || Z[i]+d >= O[j]);
}

unsigned long long minv, maxv;

void greedy() {
    minv = maxv = 0;
    int i = 0, j = 0;
    while(i < zcnt || j < ocnt) {
        if(can_receive_zero(i, j)) { i++; minv = minv * 2; }
        else { j++; minv = minv * 2 + 1; }
    }
    i = j = 0;
    while(i < zcnt || j < ocnt) {
        if(can_receive_one(i, j)) { j++; maxv = maxv * 2 + 1; }
        else { i++; maxv = maxv * 2; }
    }
}

void solve() {
    // compute Z and O
    ocnt = zcnt = 0;
    for(int i = 0; i < n; i++)
        if(K[i] == 1) O[ocnt++] = i;
        else Z[zcnt++] = i;

    // greedy to get minv, maxv
    greedy();

    // dp
    memset(f, 0, sizeof(f));
    f = 1;
    for(int i = 0; i <= zcnt; i++)
        for(int j = 0; j <= ocnt; j++) {
            if(can_receive_zero(i, j)) f[i+1][j] += f[i][j];
            if(can_receive_one(i, j)) f[i][j+1] += f[i][j];
        }
    cout << f[zcnt][ocnt] << " " << minv << " " << maxv << "\n";
}

int main() {
    int kase = 0;
    unsigned long long k;
    while(cin >> n >> d >> k) {
        for(int i = 0; i < n; i++) {
            K[n-i-1] = k % 2; k /= 2;
        }
        cout << "Case " << ++kase << ": ";
        solve();
    }
    return 0;
}

9-30 UVa1375 The Best Name for Your Baby uva1375.cpp @

// UVa1375 The Best Name for Your Baby
// Rujia Liu
#include<iostream>
#include<string>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
#include<map>
using namespace std;

const int maxn = 50 + 5;
const int maxlen = 20 + 5;
const int maxs = 50*20 + 52 + 5; // for a rule with right length x, we have x-1 symbols with length>1

int n, L, ns;
string rule[maxn];
string sym[maxs]; // symbols
int car[maxs], cdr[maxs]; // lisp names for "head" and "tail" 8-)
string dp[maxs][maxlen];

bool is_all_terminal(const string& s) {
    for(int i = 0; i < s.length(); i++)
        if(!(s[i] >= 'a' && s[i] <= 'z')) return false;
    return true;
}

string min(const string& a, const string& b) {
    if(a == "-") return b;
    return a < b ? a : b;
}

struct Node {
    int x;
    string s;
    Node(int x, string s):x(x),s(s){}
    // smaller string has higher priority, thus will be extracted earlier
    bool operator < (const Node& rhs) const {
        return s > rhs.s;
    }
};

struct Transform {
    int target, empty;
    Transform(int t, int e):target(t),empty(e){}
};

vector<Transform> tr[maxs];

bool vis[maxs];
// fill in other dp[?][len] reachable from existing dp[?][len] nodes via "epsilon edges"
void search(int len) {
    memset(vis, 0, sizeof(vis));
    priority_queue<Node> q;
    for(int i = 0; i < ns; i++)
        if(dp[i][len] != "-") {
            q.push(Node(i, dp[i][len]));
        }

    while(!q.empty()) {
        Node u = q.top(); q.pop();
        int x = u.x;
        string s = u.s;
        if(vis[x]) continue;
        vis[x] = true;
        for(int i = 0; i < tr[x].size(); i++) {
            int target = tr[x][i].target;
            int empty = tr[x][i].empty;
            if(dp[empty] == "" && (dp[target][len] == "-" || s < dp[target][len])) {
                dp[target][len] = s;
                q.push(Node(target, s));
            }
        }
    }
}

map<string,int> sym2id;

int ID(const string& s) {
    if(!sym2id.count(s)) {
        sym[ns] = s;
        sym2id[s] = ns++;
    }
    return sym2id[s];
}

// S=HT, if H can be empty, S and T can be transformed to each other
// we say h can reach s via epsilon edge t, and t can reach s via epsilon edge h
void add_intermediate_symbol(const string& S) {
    int s = ID(S);
    if(S.length() < 2) return;
    int h = ID(S.substr(0,1));
    int t = ID(S.substr(1,S.length()-1));
    tr[h].push_back(Transform(s, t));
    tr[t].push_back(Transform(s, h));
    car[s] = h;
    cdr[s] = t;
}

int main() {
    while(cin >> n >> L && n) {
        sym2id.clear();
        ns = 0;

        ID(""); // make sure sym = ""
        for(int i = 0; i < maxs; i++) tr[i].clear();

        for(int i = 0; i < n; i++) {
            cin >> rule[i]; // for example, rule[i]="S=AbC"
            int left = ID(rule[i].substr(0,1));
            int right = ID(rule[i].substr(2));
            tr[right].push_back(Transform(left, ID("")));  // AbC can be transformed to S
            int len = rule[i].length();
            for(int j = 2; j < len; j++) // AbC, bC, C
                add_intermediate_symbol(rule[i].substr(j));
        }

        for(int i = 0; i < ns; i++)
            for(int j = 0; j <= L; j++)
                dp[i][j] = "-"; // impossible
        dp = ""; // dp[i][j] means the first string with len j that symbol i can be transformed into

        for(int j = 0; j <= L; j++) {
            for(int i = 0; i < ns; i++) {
                if(sym[i].length() == j && is_all_terminal(sym[i])) dp[i][j] = sym[i];
                if(sym[i].length() < 2) continue;
                int s1 = car[i], s2 = cdr[i];
                for(int k = 1; k < j; k++) {
                    if(dp[s1][k] != "-" && dp[s2][j-k] != "-")
                        dp[i][j] = min(dp[i][j], dp[s1][k] + dp[s2][j-k]);
                }
            }
            search(j);
        }
        cout << dp[ID("S")][L] << "\n";
    }
    return 0;
}

9-31 UVa1628 Pizza Delivery UVa1628.cpp @

// UVa1628 Pizza Delivery
// Rujia Liu
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int maxn = 100 + 5;

int kase, n;
int p[maxn], v[maxn];
int d[maxn][maxn][maxn];
int vis[maxn][maxn][maxn];

// already considered s~e, still need to delivery to cnt people.
// pos = 0 means at s, pos = 1 means at e
int dp(int s, int e, int cnt, int pos) {
    if(cnt == 0) return 0;

    int &ans = d[s][e][cnt][pos];
    if(vis[s][e][cnt][pos] == kase) return ans;
    vis[s][e][cnt][pos] = kase;

    ans = 0;
    if(!pos) {
        for(int i = 0; i < s; i++)
            ans = max(ans, v[i] - cnt * abs(p[i] - p[s]) + dp(i, e, cnt - 1, 0));
        for(int i = e + 1; i < n; i++)
            ans = max(ans, v[i] - cnt * abs(p[i] - p[s]) + dp(s, i, cnt - 1, 1));
    }
    else {
        for(int i = 0; i < s; i++)
            ans = max(ans, v[i] - cnt * abs(p[i] - p[e]) + dp(i, e, cnt - 1, 0));
        for(int i = e + 1; i < n; i++)
            ans = max(ans, v[i] - cnt * abs(p[i] - p[e]) + dp(s, i, cnt - 1, 1));
    }
    return ans;
}

int main() {
    int T;
    scanf("%d",&T);
    memset(vis, 0, sizeof(vis));
    for(kase = 1; kase <= T; kase++) {
        scanf("%d", &n);
        for(int i = 0; i < n; i++) scanf("%d", &p[i]);
        for(int i = 0; i < n; i++) scanf("%d", &v[i]);

        int ans = 0;
        for(int k = 1; k <= n; k++)
            for(int i = 0; i < n; i++)
                ans = max(ans, v[i] - k * abs(p[i]) + dp(i, i, k - 1, 0));
        printf("%d\n",ans);
    }
    return 0;
}

✂️ 2016/08/20 上午 9:30:00 6. 链表 Linked List @

介绍 Dummy Node 在链表问题中的运用 Introduce Dummy Node in Linked List @
Dummy node -> sentinel node. ['sɛntɪnl]，哨兵。
Linked list @
Advantages

Linked lists are a dynamic data structure, which can grow and be pruned, allocating and deallocating memory while the program is running.

Insertion and deletion node operations are easily implemented in a linked list.

Linear data structures such as stacks and queues are easily executed with a linked list.

They can reduce access time and may expand in real time without memory overhead.

Disadvantages

They use more memory than arrays because of the storage used by their pointers.

Nodes in a linked list must be read in order from the beginning as linked lists are inherently sequential access.

Nodes are stored incontiguously（不连续地）, greatly increasing the time required to access individual elements within the list, especially with a CPU cache.

Difficulties arise in linked lists when it comes to reverse traversing. For instance, singly linked lists are cumbersome to navigate backwards and while doubly linked lists are somewhat easier to read, memory is wasted in allocating space for a back-pointer.

A singly linked list whose nodes contain two fields: an integer value and a link to the next node

A doubly linked list whose nodes contain three fields: an integer value, the link forward to the next node, and the link backward to the previous node

A circular linked list
Sentinel nodes @
In computer programming, a sentinel node is a specifically designated （指定）node used with linked lists and trees as a traversal path terminator. This type of node does not hold or reference any data managed by the data structure.

traversal, [trəˈvərs(ə)l]

Sentinels are used as an alternative over using null as the path terminator in order to get one or more of the following benefits:

Increased speed of operations

Reduced algorithmic complexity and code size

Increased data structure robustness (arguably)

a singly linked list:

struct sll_node { // one node of the singly linked list int key; struct sll_node *next; // end-of-list indicator or -> next node } sll, *first;

First version using NULL as an end-of-list indicator

// global initialization first = NULL; // before the first insertion (not shown) struct sll_node *Search(struct Node *first, int search_key) { for ( struct sll_node *node = first; node != NULL; node = node->next ) { if (node->key == search_key) { return node; } // found } return NULL; // not found }

Second version using a sentinel node:

// global variable sll_node Sentinel, *sentinel = &Sentinel; // global initialization sentinel->next = sentinel; first = sentinel; // before the first insertion (not shown) struct sll_node *SearchWithSentinelnode(struct Node *first, int search_key) { struct sll_node *node; sentinel->key = search_key; for (node = first; node->key != search_key; node = node->next) { } if (node != sentinel) return node; // found // not found return NULL; }
sequential -> array
linked -> single linked, double linked, xunhuan danlianbao, xuanhuan double linked list
sequential+linked -> static list
你必须知道的几点 Linked List 的常用技巧 Basic skills in Linked List you should know :TODO: @

TODO

两根指针算法 Two pointers @

Splitting Linked List

Given a list, split it into two sublists — one for the front half, and one for the back half. If the number of elements is odd, the extra element should go in the front list. So FrontBackSplit() on the list {2, 3, 5, 7, 11} should yield the two lists {2, 3, 5} and {7, 11}.

void FrontBackSplit( Node *head, Node **front, Node **back ) {
    if (!head) return;  // Handle empty list
    Node *front_last_node, *slow, *fast;
    slow = fast = head;
    while( fast ) {
        front_last_node = slow;
        slow = slow->next;
        fast = (fast->next) ? fast->next->next : NULL;
    }
    front_last_node->next = NULL;               // ends the front sublist
    *front = head;
    *back  = slow;
}

-----------------------------------------------
    2   3   5   7   11  #               s: slow
    ^                                   f: fast
   s,f
-----------------------------------------------
    2   3   5   7   11  #
        ^   ^
        s   f
-----------------------------------------------
    2   3   5   7   11  #
            ^       ^
            s       f
-----------------------------------------------
    2   3   5   7   11  #
                ^       ^
                s       f=0
-----------------------------------------------
    2-> 3-> 5-> #

                7-> 11  #
-----------------------------------------------
1   2   3   4
f       f       f
s   s   s

1   2   3   4   5
f       f       f   f
s   s   s   s

Linked List Cycle @

if there is a cycle in the list, then we can use two pointers travers the list. one pointer traverse one step each time, another one traverse two steps each time. so, those two pointers meet together, that means there must be a cycle inside the list.

bool hasLoop(Node *head) {
    Node *slow = head, *fast = head;
    while (slow && fast && fast->next) {
        slow = slow->next;
        fast = fast->next->next;
        if (slow == fast)
            return true;
    }
    return false;
}

This elegant algorithm is known as Floyd’s cycle finding algorithm, also called the Tortoise and hare algorithm.

refs and see also

Linked List Cycle II @

So, the idea is:

1. Using the cycle-chcking algorithm.
1. Once p1 and p1 meet, then reset p1 to head, and move p1 & p2 synchronously until p1 and p2 meet again, that place is the cycle’s start-point

class Solution {

private:
    ListNode *p1, *p2;
public:
    bool hasCycle(ListNode *head) {
        if ( !head ) { return false; }
        p1 = p2 = head;
        while ( p1 && p2 ){
            p1 = p1->next;
            if ( !p2->next ) return false;
            p2=p2->next->next;
            if (p1==p2) return true;
        }
        return false;
    }
    ListNode *detectCycle(ListNode *head) {
        if ( !hasCycle(head) ){ return NULL; }

        p1 = head;
        while (p1!=p2) {
            p1 = p1->next;
            p2 = p2->next;
        }
        return p1;
    }
};

refs and see also

Linked List Cycle II | LeetCode OJ

常见问题讲解 Frequent Questions :TODO: @

TODO

refs and see also

✂️ 2016/08/21 上午 9:30:00 7. 数组与数 Array & Numbers @

旋转排序数组相关问题与三步翻转法的运用 Rotated Sorted Array & 3-step Reversion

just this picture:

两个排序数组的中位数 Median of Two Sorted Array @

There are two sorted arrays nums1 and nums2 of size m and n respectively.

Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).

Example 1:

nums1 = [1, 3]
nums2 =

The median is 2.0

Example 2:

nums1 = [1, 2]
nums2 = [3, 4]

The median is (2 + 3)/2 = 2.5

class Solution {
public:
    double findMedianSortedArrays(const vector<int>& A, const vector<int>& B) {
        const int m = A.size();
        const int n = B.size();
        int total = m + n;
        if (total & 0x1)
            return find_kth(A.begin(), m, B.begin(), n, total / 2 + 1);
        else
            return (find_kth(A.begin(), m, B.begin(), n, total / 2)
                    + find_kth(A.begin(), m, B.begin(), n, total / 2 + 1)) / 2.0;
    }

private:
    static int find_kth(std::vector<int>::const_iterator A, int m,
            std::vector<int>::const_iterator B, int n, int k) {
        //always assume that m is equal or smaller than n
        if (m > n) return find_kth(B, n, A, m, k);  // 0 <= m <= n
        if (m == 0) return *(B + k - 1);
        if (k == 1) return min(*A, *B);

        //divide k into two parts
        int ia = min(k / 2, m), ib = k - ia;
        if (*(A + ia - 1) < *(B + ib - 1))
            return find_kth(A + ia, m - ia, B, n, k - ia);
        else if (*(A + ia - 1) > *(B + ib - 1))
            return find_kth(A, m, B + ib, n - ib, k - ib);
        else
            return A[ia - 1];
    }
};

class Solution {
public:
    double findMedianSortedArrays(vector<int> &a, vector<int> &b) {
        int m = a.size(), n = b.size(), i = 0, j = 0, k = m+n-1 >> 1;
        while (k > 0) {
            int p = k-1 >> 1;
            if (j+p >= n || i+p < m && a[i+p] < b[j+p])
                i += p+1;
            else
                j += p+1;
            k -= p+1;
        }
        int s = j >= n || i < m && a[i] < b[j] ? a[i++] : b[j++];
        return m+n & 1 ? s : (j >= n || i < m && a[i] < b[j] ? s+a[i] : s+b[j]) * 0.5;
    }
};

TODO, leetcode tijie.

refs and see also

Median of Two Sorted Arrays | LeetCode OJ

重复元素 @

Remove Duplicates from Sorted Array | LeetCode OJ @

不允许重复。

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int j = 0;
        for (auto x: nums)
        if (!j || nums[j-1] != x)           // !j --> j == 0
            nums[j++] = x;
        return j;
    }
};

STL:

class Solution {
public:
    int removeDuplicates( vector<int>& nums ) {
        return distance( nums.begin(), unique(nums.begin(), nums.end()) );
    }
};

Remove Duplicates from Sorted Array II | LeetCode OJ @

允许最多两次重复。

class Solution {
public:
    int removeDuplicates(vector<int> &a) {
        int j = 0;
        for (auto x: a)
            if (j < 2 || a[j-1] != x || a[j-2] != x)
                a[j++] = x;
        return j;
    }
};

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        if (nums.size() <= 2) { return nums.size(); }
        int index = 2;
        for (int i = 2; i < nums.size(); i++){
            if (nums[i] != nums[index - 2])
                nums[index++] = nums[i];
        }

        return index;
    }
};

子数组相关问题 SubArray @
Maximum subarray @
DP.

f[j] = max( f[j-1]+S[j], S[j] ), j = 2..n, f = S

target = max{ f[j] }, j = 1..n

代码：

// Time: O(n), Space: O(1) int maxSubArray( vector<int> &nums ) { int result = INT_MIN, f = 0; for( int i = 0; i < nums.size(); ++i ) { f = max( f+nums[i], nums[i] ); result = max( f, result ); } return result; }

If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.

refs and see also

Maximum subarray problem - Wikipedia, the free encyclopedia

Maximum Subarray | LeetCode OJ
Subset sum problem @
refs and see also

Subset sum problem - Wikipedia, the free encyclopedia
两根指针与 x-sum 问题 Two Pointers & x-sum :TODO: @

TODO
分割数组相关问题 Partition Array

✂️ 2016/08/27 上午 9:30:00 8. 数据结构 Data Structure @

线性数据结构 @

队列的原理、实现和运用, Queue @

yangzi triangle @

#include <queue>
#include <stdio.h>
using namespace std;
void yanghui_triangle(const int n);
int main() { yanghui_triangle( 5 ); }

void yanghui_triangle(const int n) {
    int i = 1;
    queue<int> q;
    q.push(i);                                  // 预先放入第一行的 1

    for(i = 0; i <= n; i++) {                   // 逐行处理
        int j;
        int s = 0;
        q.push(s);                              // 在各行间插入一个0

        for(j = 0; j < i+2; j++) {              // 处理第 i 行的 i+2 个系数（包括一个 0）
            int t = q.front(); q.pop();
            q.push( t+s );
            s = t;                              // 打印一个系数，第 i+2 个是 0
            if(j != i+1) {
                printf("%d ",t);
            }
        }
        printf("\n");
    }
}

TODO

                                        |   queue
----------------------------------------+---------------------------
i = 0, j = [0, i+2), push 2 times       |   1
push 0                                  |   1   0
withdraw t=1                            |
push( t=1 + s=0 )                       |   0   1
s=t=1                                   |
withdraw t=0                            |
push( t=0 + s=1 )                       |
                                        |   1   1
----------------------------------------+---------------------------
i = 1, j = [0, i+2), push 3 times       |   1   1
push 0                                  |   1   1   0
withdraw t=1, push(t=1+s=0)             |   1   0   1
s=t=1                                   |
withdraw t=1, push(t=1+s=1)             |   0   1   2
s=t=1                                   |
withdraw t=0, push(t=0+s=1)             |   1   2   1
----------------------------------------+---------------------------
i = 2, j = [0, i+2), push 4 times       |   1   2   1
push 0                                  |   1   2   1   0
t=1, push(t=1+s=0), s=1                 |   2   1   0   1
t=2, push(t=2+s=1), s=2                 |   1   0   1   3
t=1, push(t=1+s=2), s=1                 |   0   1   3   3
t=0, push(t=0+s=1), s=0                 |   1   3   3   1
----------------------------------------+---------------------------
i = 3, j = [0, i+2), push 5 times       |   1   3   3   1
push 0                                  |   1   3   3   1   0
t=1, push(t=1+s=0), s=1                 |   3   3   1   0   1
t=3, push(t=3+s=1), s=3                 |   3   1   0   1   4
t=3, push(t=3+s=3), s=3                 |   1   0   1   4   6
t=1, push(t=1+s=3), s=1                 |   0   1   4   6   4
t=0, push(t=0+s=1), s=0                 |   1   4   6   4   1
----------------------------------------+---------------------------
i = 4, j = [0, i+2), push 6 times       |   1   4   6   4   1
push 0                                  |   1   4   6   4   1   0
t=1, push(t=1+s=0), s=1                 |   4   6   4   1   0   1
t=4, push(t=4+s=1), s=4                 |   6   4   1   0   1   5
t=6, push(t=6+s=4), s=6                 |   4   1   0   1   5   10
t=4, push(t=4+s=6), s=4                 |   1   0   1   5   10  10
t=1, push(t=1+s=4), s=1                 |   0   1   5   10  10  5
t=0, push(t=0+s=1), s=0                 |   1   5   10  10  5   1
...

1                   i=0                 (a+b)^0 = 1
1 1                 i=1                 (a+b)^1 = a + b
1 2 1               i=2                 (a+b)^2 = a^2 + 2ab + b^2
1 3 3 1             i=3                 (a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3
1 4 6 4 1           i=4                 ...
1 5 10 10 5 1       i=6                 ...

栈的原理、实现和运用, Stack :TODO: @

TODO

哈希表的原理、实现和运用, HashMap @

hash table @

Open addressing - Wikipedia, the free encyclopedia @
Open addressing, or closed hashing, is a method of collision resolution in hash tables. With this method a hash collision is resolved by probing, or searching through alternate locations in the array (the probe sequence) until either the target record is found, or an unused array slot is found, which indicates that there is no such key in the table. Well known probe sequences include:
```
record pair { key, value }
var pair array slot[0..num_slots-1]

function find_slot(key)
    i := hash(key) modulo num_slots
    // search until we either find the key, or find an empty slot.
    while (slot[i] is occupied) and ( slot[i].key ≠ key )
        i = (i + 1) modulo num_slots
    return i
```
- Linear probing
  
  in which the interval between probes is fixed — often at 1.
- Quadratic probing
  
  in which the interval between probes increases linearly (hence, the indices are described by a quadratic function).
- Double hashing
  
  in which the interval between probes is fixed for each record but is computed by another hash function.
Open Addressing 思想非常简单。如果第一次 Hash 寻找到得位置失败，那就不断进行位移，直到找到满足条件的位置。
Linear probing
优点：思路简单，而且只要 Hash 表不满，总能找到满足条件的位置。

缺点：容易产生主聚合效应（primary clustering）。简单来说，就是插入的点容易聚集到一块地方，从而使得第一次 Hash 到这块范围的数都必须顺序搜索这块范围。根据复杂的计算，我们可以得到，当 load factor（此概念在上一章介绍）为 0.5 时，平均每次插入（等同于非成功寻找）需要位移 2.5 次，平均每次成功寻找需要位移 1.5 次。将 load factor 保证在 0.5 以下，那么时间是比较理想的。
Linear probing
顾名思义，就是 Function(i) = i^2。简单地计算可以得到：h(i+1)(x) = hi(x) + 2i -1. 另外，只有当 load factor 小于 0.5 且 Hash 表大小为质数时，才能保证每次插入都成功（可以证明，这里略）。

优点：不会产生主聚合效应。

缺点：虽然 Quadratic 方法不会产生主聚合效应。但会产生次聚合效应（secondary clustering）。即，第一次 Hash 到同一个位置的点，他们之后的搜索过程都完全一样，需要重复。
延迟删除（lazy deletion）

如果我们需要删除一个值，不能简单的把那个位置的值去掉。简单思索便可明白，因为这个点后面的值可能是通过位移过去的，如果这点被挖空，那么我们想寻找后面的值就变得不可能了。

因此，我们使用一个延迟删除的技术。思想很简单，我们给每个点赋予一个状态，分别是被占用（legitimate, [ləˈdʒɪtəmɪt], 合法的；正当的），空（empty），被删除（deleted）。初始时所有点都为空，当被插入一个值时将状态设为被占用，但被删除时状态设为被删除。这样的话，如果我们要寻找一个点，只要搜索路径上的点非空，且其值与我们想要搜索的值不同，那么就不断搜索下去，直到找到空点或者相同值得点。（如果觉得拗口，请看下面的代码）。
假設整個 hash table 的數據不在 cache。因為是開放尋址，每次 collision 要再跳到另一個 slot（即 probing），hash table 越滿就會有越多次跳轉，產生較多 cache miss。

若整個 hash table 都能儲存在 cache，怎樣做都不會出現 cache miss。

但考慮 hash table 遠大於 cache 大小時，可以理解為每次不同的 hashing 都會 cache miss，collision 和 cache miss 的概率成正比。

refs and see also
- 《数据结构》学习– Hash(3) –Open Addressing - 江饭 - 博客频道 - CSDN.NET
- 使用 open addressing 的 Hash 表载荷过高为什么会降低 CPU 的缓存命中率？ - 知乎

hash table @

哈希表处理冲突有两种方式，开地址法 (Open Addressing) 和闭地址法 (Closed Addressing)。

闭地址法也即拉链法 (Chaining)，每个哈希地址里不再是一个元素，而是链表的首地址。

开地址法有很多方案，有线性探测法 (Linear Probing)、二次探测法 (Quadratic Probing) 和双散列法 (Double Hashing) 等。

下面是拉链法的 C 语言实现。

template<typename elem_t>
int elem_hash(const elem_t &e);

template<typename elem_t>
bool operator==(const elem_t &e1, const elem_t &e2);

template<typename elem_t>
class hash_set {
public:
    hash_set(int prime, int capacity);
    ~hash_set();
    bool find(const elem_t &elem);                  // 查找某个元素是否存在.
    bool insert(const elem_t &elem);                // 添加一个元素，如果已存在则添加失败.
private:
    int prime;                                      // 哈希表取模的质数，也即哈希桶的个数，小于 capacity
    int capacity;                                   // 哈希表容量，一定要大于元素最大个数

    int *head;                                      // head[PRIME], 首节点下标

    struct node_t {
        elem_t elem;
        int next;
        node_t():next(-1) {}
    } *node;                                        // node[HASH_SET_CAPACITY], 静态链表

    int size;
};

template<typename elem_t>
hash_set<elem_t>::hash_set( int prime, int capacity ) {
    this->prime = prime;
    this->capacity = capacity;
    head = new int[prime];
    node = new node_t[capacity];
    fill( head, head + prime, -1 );
    fill( node, node + capacity, node_t() );
    size = 0;
}

template<typename elem_t>
hash_set<elem_t>::~hash_set() {
    this->prime = 0;
    this->capacity = 0;
    delete[] head;
    delete[] node;
    head = NULL;
    node = NULL;
    size = 0;
}

template<typename elem_t>
bool hash_set<elem_t>::find(const elem_t &elem) {
    for( int i = head[elem_hash(elem)]; i != -1; i = node[i].next ) {
        if( elem == node[i].elem ) { return true; }
    }
    return false;
}

template<typename elem_t>
bool hash_set<elem_t>::insert(const elem_t &elem) {
    const int hash_code = elem_hash(elem);
    if( find(elem) ) { return false; }
    node[size].next = head[hash_code]; // 不存在，则插入在首节点之前
    node[size].elem = elem;
    head[hash_code] = size++;
    return true;
}

babelfish (easy, use dict.find) @

input:

dog ogday
cat atcay
pig igpay
froot ootfray
loops oopslay

atcay
ittenkay
oopslay

output:

cat
eh
loops

/* POJ 2503 Babelfish , http://poj.org/problem?id=2503 */
#include <cstdio>
#include <map>
#include <string>
#include <cstring>

using namespace std;

/** 字符串最大长度 */
const int MAX_WORD_LEN = 10;

int main() {
    char line[MAX_WORD_LEN * 2 + 1];
    char s1[MAX_WORD_LEN + 1], s2[MAX_WORD_LEN + 1];
    map<string, string> dict;

    while ( fgets(line, MAX_WORD_LEN*2, stdin ) && (line != 0 && line != '\n') ) {
        sscanf(line, "%s %s", s1, s2);
        dict[s2] = s1;
    }

    while ( fgets(line, MAX_WORD_LEN*2, stdin ) ) {
        sscanf( line, "%s", s1 );
        // you should not use dict[s1].length() == 0
        if ( dict.find(s1) != dict.end() ) {
            puts("eh");
        } else {
            printf("%s\n", dict[s1].c_str());
        }
    }
    return 0;
}

cat fish.txt | ./a.out

c++ version, buggy…

#include <iostream>
#include <map>
#include <string>
#include <sstream>
#include <stdio.h>

using namespace std;

int main() {
    string line;
    map<string, string> dict;

    while ( getline( cin, line ) && !line.empty() ) {
        stringstream ss( line );
        string s1, s2;
        ss >> s1 >> s2;
        dict[s2] = s1;
        // printf( "s1: %s, s2: %s\n", s1.c_str(), s2.c_str() );
    }

    while ( cin >> line && !line.empty() ) {
        if ( dict.find(line) != dict.end() ) {
            cout << "eh" << endl;
        } else {
            cout << dict[line] << endl;
        }
    }
    return 0;
}

树形数据结构 @

堆的原理、实现和运用, Heap @

Heap (data structure) - Wikipedia, the free encyclopedia @

In computer science, a heap is a specialized tree-based data structure that satisfies the heap property: If A is a parent node of B then the key (the value) of node A is ordered with respect to the key of node B with the same ordering applying across the heap. A heap can be classified further as either a “max heap” or a “min heap”. In a max heap, the keys of parent nodes are always greater than or equal to those of the children and the highest key is in the root node. In a min heap, the keys of parent nodes are less than or equal to those of the children and the lowest key is in the root node. Heaps are crucial in several efficient graph algorithms such as Dijkstra’s algorithm, and in the sorting algorithm heapsort. A common implementation of a heap is the binary heap, in which the tree is a complete binary tree.

Example of a complete binary max-heap with node keys being integers from 1 to 100

When a heap is a complete binary tree, it has a smallest possible height—a heap with N nodes always has (logN) height. A heap is a useful data structure when you need to remove the object with the highest (or lowest) priority.

Heapsort - Wikipedia, the free encyclopedia @
```
iParent(i)     = floor((i-1) / 2)
iLeftChild(i)  = 2*i + 1
iRightChild(i) = 2*i + 2

procedure heapsort(a, count) is
    input: an unordered array a of length count

    (Build the heap in array a so that largest
    value is at the root) heapify(a, count)

    (The following loop maintains the invariants
    that a[0:end] is a heap and every element
    beyond end is greater than everything before it
    (so a[end:count] is in sorted order))

    end ← count - 1
    while end > 0 do
        // a is the root and largest value. The
        // swap moves it in front of the sorted
        // elements.)
        swap(a[end], a)
        // the heap size is reduced by one
        end ← end - 1
        // the swap ruined the heap property, so restore it
        siftDown(a, 0, end)
```

heap.c @

#include <stdlib.h>                             // malloc
#include <string.h>                             // memcpy
typedef struct heap_t {
    int size;
    int capacity;
    int *elems;
    int (*cmp)(const int *, const int *);       // compare function
} heap_t;

int cmp_int( const int *x, const int *y ) {
    int sub = *x - *y;
    return sub > 0 ? 1 : sub < 0 ? -1 : 0;
}

heap_t * heap_create( const int capacity,
                      int (*cmp)(const int *, const int *) )
{
    heap_t *h = (heap_t*)malloc(sizeof(heap_t));
    h->size = 0;
    h->capacity = capacity;
    h->elems = (int *)malloc(capacity * sizeof(int));
    h->cmp = cmp;
    return h;
}

void heap_destroy( heap_t *h ) {
    free( h->elems );
    free( h );
}

int heap_empty( const heap_t *h ) {
    return h->size == 0;
}

int heap_size( const heap_t *h ) {
    return h->size;
}

sift down
---------

3   9   6   8   5   1   4   2   7           9   8   6   7   5   1   4   2   3
                                                       9
            /   \                                       /   \
           /      \                                    /      \
         9         6                                 8         6
        /  \       /  \                             /  \       /  \
      8     5     1    4                          7     5     1    4
     / \                                         / \
    2    7                                      2
                        tmp = h[j]

    (i)         can go down?
    /\
   /  \             j or j+1 ?
  /    \            h[i]    =   h[j]
(j)   (j+1)         h[i]    =   tmp

void heap_sift_down( const heap_t *h, const int start ) {       // 小根堆的自上向下筛选算法.
    int i = start;
    const int tmp = h->elems[start];

    // 2*i+1: left child, 2*i+2: right child
    for( int j = 2*i+1; j < h->size; j = 2*j+1 ) {
        if( j+1 < h->size && h->cmp(&(h->elems[j]), &(h->elems[j + 1])) > 0 ) {
            j++;                                    // sift towards j, j 指向两子女中小者
        }
        if( h->cmp(&tmp, &(h->elems[j])) <= 0 ) {   // they are all big guys down there.
            break;
        } else {
            h->elems[i] = h->elems[j];
            i = j;
        }
    }
    h->elems[i] = tmp;
}

                        tmp = h[j]

           (i)          can go up?
           /\
          /  \              h[j]    =   h[i]
         /    \             j       =   i
       (j)     *            i       =   (j-1)/2

// 小根堆的自下向上筛选算法.
void heap_sift_up( const heap_t *h, const int start ) {
    const int tmp = h->elems[start];
    int j = start;
    int i= (j - 1) / 2;                             // parent
    while( j > 0 ) {
        if( h->cmp(&(h->elems[i]), &tmp) <= 0 ) {   // parent is small enough
            break;
        } else {
            h->elems[j] = h->elems[i];
            j = i;
            i = (j-1)/2;
        }
    }
    h->elems[j] = tmp;
}

void heap_push( heap_t *h, const int x ) {
    if( h->size == h->capacity ) {
        h->capacity *= 2;
        int *tmp = (int *)realloc( h->elems, h->capacity*sizeof(int) );
        h->elems = tmp;
    }
    h->elems[h->size++] = x;                        // append
    heap_sift_up( h, h->size - 1 );                 // sift up last node
}

void heap_pop( heap_t *h ) {
    h->elems = h->elems[h->size - 1];
    --h->size;
    heap_sift_down( h, 0 );
}

int heap_top( const heap_t *h ) {
    return h->elems;
}

Minimum N, (heap, priority_queue) ♥️ @

#include <cstdio>
#include <queue>
#include <algorithm>
#include <functional>
using namespace std;

int N;
const int MAXN = 100000;
int a[MAXN], b[MAXN];

typedef struct node_t {
    int sum;
    int b;                                          // b is the index, init with 0, sum=a[i]+b[b=0]
    bool operator>( const node_t &other ) const {   // std::greater<node_t>
        return sum > other.sum;
    }
} node_t;

void k_merge() {
    sort( a, a+N );
    sort( b, b+N );
    priority_queue< node_t, vector<node_t>, greater<node_t> > q;    // a min heap

    for( int i = 0; i < N; ++i ) {
        node_t tmp;
        tmp.b = 0;
        tmp.sum = a[i]+b[tmp.b];
        q.push( tmp );
    }

    for( int i = 0; i < N; ++i ) {
        node_t tmp = q.top(); q.pop();
        printf("%d ", tmp.sum);
        tmp.sum = tmp.sum - b[tmp.b] + b[tmp.b + 1];
        ++tmp.b;
        q.push(tmp);
    }
}

int main() {
    scanf( "%d", &N );
    for( int i = 0; i < N; ++i ) {
        scanf( "%d", &a[i] );
    }
    for( int i = 0; i < N; ++i ) {
        scanf( "%d", &b[i] );
    }
    k_merge();
    return 0;
}

$ cat input.txt
5
1   3   2   4   5
6   3   4   1   7

$ cat input.txt | ./a.out
2 3 4 4 5

数学概念与方法 @
- 数论初步 @
  
  欧几里德算法和唯一分解定理 @
  
  捻转相除法
  
  int gcd( int a, int b ) { return b == 0 ? a : gcd( b, a%b ); }
- 计数与概率基础
- 其他数学专题
- 竞赛题目选讲
- 训练参考

✂️ 2016/08/28 上午 9:30:00 9. 图与搜索 Graph & Search @

稠密图适合用邻接矩阵来表示 @

// 顶点数最大值
const int MAX_NV = 100;

// 边的权值类型，可以为 int, float, double.
typedef int graph_weight_t;
const graph_weight_t GRAPH_INF = INT_MAX;

// 图，用邻接矩阵 (Adjacency Matrix).
struct graph_t {
    int nv;                                         // 顶点数
    int ne;                                         // 边数
    graph_weight_t matrix[MAX_NV][MAX_NV];          // 邻接矩阵，存放边的信息，如权重等
};

稀疏图适合用邻接表来表示 @

// 边的权值类型，可以为 int, float, double
typedef int graph_weight_t;

// 顶点的编号，可以为 char, int, string 等
typedef char graph_vertex_id_t;

// 图，用邻接表 (Adjacency List).
struct graph_t {
    int nv;                                         // 顶点数
    int ne;                                         // 边数
    map<
        graph_vertex_id_t,
        map<graph_vertex_id_t, graph_weight_t>
    > matrix;                                       // 邻接表，存放边的信息，如权重等
};

图的深搜 DFS @

图的 DFS, 搜索边 @

//  图的深度优先搜索代码框架，搜索边.
//  g 图
//  u 出发顶点
//  visited 边的访问历史记录
void dfs( const graph_t &g, int u, bool visited[][MAX_NV] ) {
    for( int v = 0;  v < g.nv; ++v ) {
        if( g.matrix[u][v] && !visited[u][v] ) {
            visited[u][v] = visited[v][u] = true;   // 无向图用这句
            // visited[u][v] = true;                // 有向图用这句
            dfs( g, v, visited );
            // 这里写逻辑代码, e.g. printf("%d %d\n", u, v);
        }
    }
}

图的 DFS, 搜索顶点 @

//  图的深度优先搜索代码框架，搜索顶点.
//  g 图
//  u 出发顶点
//  visited 顶点的访问历史记录
void dfs( const graph_t &g, int u, bool visited[MAX_NV] ) {
    visited[u] = true;
    for( int v = 0;  v < g.nv; ++v ) {
        if( g.matrix[u][v] && !visited[v] ) {
            dfs(g, v, visited);
            // 这里写逻辑代码, e.g. printf("%d %d\n", u, v);
        }
    }
}

Satellite Photographs @

Farmer John purchased satellite photos of W * H pixels of his farm (1 <= W <= 80, 1 <= H <= 1000) and wishes to determine the largest ‘contiguous’ (connected) pasture. Pastures are contiguous when any pair of pixels in a pasture can be connected by traversing adjacent vertical or horizontal pixels that are part of the pasture. (It is easy to create pastures with very strange shapes, even circles that surround other circles.)

Each photo has been digitally enhanced to show pasture area as an asterisk (*) and non-pasture area as a period (.). Here is a 10x5 sample satellite photo:

..*.....**
.**..*****
.*...*....
..****.***
..****.***

This photo shows three contiguous pastures of 4, 16, and 6 pixels. Help FJ find the largest contiguous pasture in each of his satellite photos.

输入

    Line  1:        Two space-separated integers: W and H
    Lines 2..H+1:   Each line contains W "*" or "."
                    characters representing one raster line of
                    a satellite photograph.

    10 5
    ..*.....**
    .**..*****
    .*...*....
    ..****.***
    ..****.***

输出

    Line 1:         The size of the largest contiguous field in the satellite photo.

    16

这是一个平面的二维地图，把地图上的每个点当成隐式图上的一个顶点，每个顶点有上下左右四个邻接点。在这个隐式图上进行深搜。

too easy…

// POJ 3051 Satellite Photographs, http://poj.org/problem?id=3051
#include <stdio.h>
#include <string.h>
#include <vector>

using namespace std;

void dfs( vector<vector<char> > &map, int x, int y, int &count ) {
    if( map[x][y] == '.' ) { return; }  // 加了一圈 '.' 可以防止越界，因此不需要判断越界

    map[x][y] = '.';                    // 标记 (x,y) 已访问过，起到去重作用
    ++count;
    dfs( map, x+1, y,   count );
    dfs( map, x-1, y,   count );
    dfs( map, x,   y+1, count );
    dfs( map, x,   y-1, count );
}

int main() {
    int W, H;
    while( 2 == scanf( "%d%d", &W, &H ) ) {
        vector<vector<char> > map( H+2, vector<char>(W+2, '.') );
        for( int i = 1; i <= H; ++i ) {
            char line[100];
            scanf( "%s", line );
            strncpy( &map[i][1], line, W ); // will not append '\0'
        }

        int ret = 0;
        for( int i = 1; i <= H; ++i ) {
            for( int j = 1; j <= W; ++j ) {
                int count = 0;
                if( map[i][j] == '*' ) {
                    dfs( map, i, j, count );
                }
                ret = max( ret, count );
            }
        }
        printf( "%d\n", ret );
    }
    return 0;
}

John’s trip @

Little Johnny has got a new car. He decided to drive around the town to visit his friends. Johnny wanted to visit all his friends, but there was many of them. In each street he had one friend. He started thinking how to make his trip as short as possible. Very soon he realized that the best way to do it was to travel through each street of town only once. Naturally, he wanted to finish his trip at the same place he started, at his parents’ house.

The streets in Johnny’s town were named by integer numbers from 1 to n, n < 1995. The junctions were independently named by integer numbers from 1 to m, m <= 44. No junction connects more than 44 streets. All junctions in the town had different numbers. Each street was connecting exactly two junctions. No two streets in the town had the same number. He immediately started to plan his round trip. If there was more than one such round trip, he would have chosen the one which, when written down as a sequence of street numbers is lexicographically the smallest. But Johnny was not able to find even one such round trip.

Help Johnny and write a program which finds the desired shortest round trip. If the round trip does not exist the program should write a message. Assume that Johnny lives at the junction ending the street appears first in the input with smaller number. All streets in the town are two way. There exists a way from each street to another street in the town. The streets in the town are very narrow and there is no possibility to turn back the car once he is in the street.

Input

    Input file consists of several blocks. Each block describes one town. Each
    line in the block contains three integers x, y, z, where x > 0 and y > 0
    are the numbers of junctions which are connected by the street number z.
    The end of the block is marked by the line containing x = y = 0. At the end
    of the input file there is an empty block, x = y = 0.

    1 2 1
    2 3 2
    3 1 6
    1 2 5
    2 3 3
    3 1 4
    0 0
    1 2 1
    2 3 2
    1 3 3
    2 4 4
    0 0
    0 0

Output

    Output one line of each block contains the sequence of street numbers
    (single members of the sequence are separated by space) describing Johnny's
    round trip. If the round trip cannot be found the corresponding output
    block contains the message "Round trip does not exist."

    1 2 3 5 4 6
    Round trip does not exist.

分析

欧拉回路。

如果能从图的某一顶点出发，每条边恰好经过一次，这样的路线称为欧拉道路 (Eulerian Path)。如果还能够回到起点，这样的路线称为欧拉回路 (Eulerian Circuit)。

对于无向图 G，当且仅当 G 是连通的，且最多有两个奇点，则存在欧拉道路。如果有两个奇点，则必须从其中一个奇点出发，到另一个奇点终止。

如果没有奇点，则一定存在一条欧拉回路。

对于有向图 G，当且仅当 G 是连通的，且每个点的入度等于出度，则存在欧拉回路。

如果有两个顶点的入度与出度不相等，且一个顶点的入度比出度小 1，另一个顶点的入度比出度大 1，此时，存在一条欧拉道路，以前一个顶点为起点，以后一个顶点为终点。

// POJ 1041 John's trip, http://poj.org/problem?id=1041
#include <iostream>
#include <cstring>
#include <algorithm>
#include <stack>

using namespace std;

const int MAX_NV = 45;
const int MAX_NE = 1996;

struct graph_t {
    int nv;
    int ne;
    int matrix[MAX_NV][MAX_NE];     // G[点][边] = 点，这样是为了能方便让边 lexicographically 输出
} G;

bool visited[MAX_NE];               // 边是否已访问
int  degree[MAX_NV];                // 点的度

stack<int> s;                       // 栈，用于输出

void stack_print( stack<int> &s ) {
    while( !s.empty() ) {
        cout << s.top() << " ";
        s.pop();
    }
    cout << "\n";
}

void euler( int u ) {
    for( int e = 1; e <= G.ne; ++e ) {
        if( !visited[e] && G.matrix[u][e] ) {
            visited[e] = true;
            euler( G.matrix[u][e] );
            s.push( e );
        }
    }
}

int main() {
    int x, y, z, start;
    while( (cin >> x >> y) && x && y ) {
        memset( visited,    false,  sizeof(visited) );
        memset( degree,     0,      sizeof(degree)  );
        memset( &G,         0,      sizeof(G)       );

        start = x < y ? x : y;
        cin >> z;
        G.ne = max( G.ne, z );
        G.nv = max( G.nv, max(x, y) );
                                        // input: x (node), y (node), z (edge)
        G.matrix[x][z] = y;             // x ---z---> y
        G.matrix[y][z] = x;             // y ---z---> x
        ++degree[x];
        ++degree[y];

        while( (cin >> x >> y) && x && y ) {
            cin >> z;
            G.ne = max( G.ne, z );
            G.nv = max( G.nv, max(x, y) );
            G.matrix[x][z] = y;
            G.matrix[y][z] = x;
            ++degree[x];
            ++degree[y];
        }

        // 欧拉回路形成的条件之一，判断结点的度是否为偶数
        bool valid = true;
        for( int i = 1; i <= G.nv; ++i ) {
            if( degree[i] & 1 ) {
                valid = false;
                break;
            }
        }

        if( !valid ) {
            cout << "Round trip does not exist.\n";
        } else {
            euler( start );
            stack_print(s);
        }
    }
    return 0;
}

Abbott 的复仇 ♥️ @

// d[r][c][dir] 存储从初始状态到 (r,c,dir) 的最短长度，其父节点保存在
// p[r][c][dir]
// has_edge[r][c][dir][turn], now at (r,c,dir), can `turn`?
//  inside(r, c), inside the map

const char *dirs  = "NESW"; // north, east, south, west
const char *turns = "FLR";  // forward, left, right
int dir_id(  char c ) { return strchr(dirs, c) - dirs; }
int turn_id( char c ) { return strchr(turns, c) - turns; }

//   clockwise :    N   E   S   W           //          +-----------> y (col-wise)
const int dr[] = { -1,  0,  1,  0 };        //          |
const int dc[] = {  0,  1,  0, -1 };        //          |
                                            //          | x (row-wise)
                                            //          V

Node walk( const Node &u, int turn ) {
    int dir = u.dir;                        // turn = 0, forward
    if( turn == 1 ) { dir = (dir+3)%4; }    // turn = 1, left, counter clockwise
    if( turn == 2 ) { dir = (dir+1)%4; }    // turn = 2, right, clockwise
    return Node( u.r + dr[dir], u.c + dc[dir], dir );
}

void solve() {
    queue<Node> q;
    memset( d, -1, sizeof(d) );             // reset to -1
    Node u( r1, c1, dir );                  // start pos
    d[u.r][u.c][u.dir] = 0;                 // init distance
    q.push( u );
    while( !q.empty() ) {
        Node u = q.front(); q.pop();
        if( u.r == r2 && r.c == c2 ) { print_ans(u); return; }
        for( int i = 0; i < 3; ++i ) {      // enum turns
            Node v = walk( u, i );
            if( has_edge[u.r][u.c][u.dir][i] &&
                inside(v.r, v.c) &&
                d[v.r][v.c][v.dir] < 0 ) {  // 以前没有处于这个姿态
                // advance
                d[v.r][v.c][v.dir] = d[u.r][u.c][u.dir] + 1;
                p[v.r][v.c][v.dir] = u;
                q.push( v );                // 当前位置总是再 stack 顶端存着
            }
        }
    }
    printf( "No Solution Possible.\n" );
}

void print_ans( Node u ) {
    vector<Node> nodes;
    for( ;; ) {
        nodes.push_back( u );                   // 一路存起来
        if( d[u.r][u.c][u.dir] == 0 ) break;    // origin
        u = p[u.r][u.c][u.dir];                 // backtrace
    }
    nodes.push_back( Node(r1, c1, dir) );       // origin: r0, c0

    int cnt = 0;
    for( int i = nodes.size()-1; i >= 0; --i ) {
        if( cnt % 10 == 0 ) { printf( " " ); }
        printf( " (%d, %d)", nodes[i].r, nodes[i].c );
        if( ++cnt % 10 == 0 ) {
            printf( "\n" );
        }
    }
    if( nodes.size() % 10 != 0 ) { printf( "\n" ); }
}

The Necklace buggy? @

My little sister had a beautiful necklace made of colorful beads. Two successive beads in the necklace shared a common color at their meeting point. The figure below shows a segment of the necklace:

   +-----------+   +-----------+   +-------------+   +------------+
---| green|red |---| red|white |---| white|green |---| green|blue |---
   +-----------+   +-----------+   +-------------+   +------------+

But, alas! One day, the necklace was torn and the beads were all scattered over the floor. My sister did her best to recollect all the beads from the floor, but she is not sure whether she was able to collect all of them. Now, she has come to me for help. She wants to know whether it is possible to make a necklace using all the beads she has in the same way her original necklace was made and if so in which order the bids must be put.

Please help me write a program to solve the problem.

Input

    The input contains T test cases. The first line of the
    input contains the integer T.

    The first line of each test case contains an integer N
    (5 <= N <= 1000) giving the number of beads my sister
    was able to collect. Each of the next N lines contains
    two integers describing the colors of a bead. Colors
    are represented by integers ranging from 1 to 50.

    2
    5
    1 2
    2 3
    3 4
    4 5
    5 6
    5
    2 1
    2 2
    3 4
    3 1
    2 4

Output

    For each test case in the input first output the test
    case number as shown in the sample output. Then if you
    apprehend that some beads may be lost just print the
    sentence ``some beads may be lost" on a line by itself.
    Otherwise, print N lines with a single bead description
    on each line. Each bead description consists of two
    integers giving the colors of its two ends.
    For 1 <= i <= N_1, the second integer on line i must be
    the same as the first integer on line i + 1.
    Additionally, the second integer on line N must be
    equal to the first integer on line 1. Since there are
    many solutions, any one of them is acceptable.

    Print a blank line between two successive test cases.

    Case #1
    some beads may be lost

    Case #2
    2 1
    1 3
    3 4
    4 2
    2 2

欧拉回路。

注意顶点可以有自环。

#include <stdio.h>
#include <string.h>

#define MAXN 51                         // 顶点最大个数

int G[MAXN][MAXN];
int visited[MAXN];
int count[MAXN];                        // 顶点的度

void dfs( int u ) {
    visited[u] = 1;
    for( int v = 0;  v < MAXN; ++v ) {
        if( G[u][v] && !visited[v] ) {
            dfs(v);
        }
    }
}

// 欧拉回路，允许自环和重复边
void euler( int u ) {
    for( int v = 0; v < MAXN; ++v ) {
        if( G[u][v] ) {
            --G[u][v]; --G[v][u];       // 这个技巧，即有 visited 的功能，又允许重复边
            printf( "%d %d\n", u, v );  // 逆向打印，或者存到栈里再打印
            euler(v);
        }
    }
}

int main() {
    int cases = 0, T;
    scanf( "%d", &T );
    while( T-- ) {
        bool validGraph = true;         // 结点的度是否为偶数
        bool connected  = true;         // 图是否是连通的
        memset( G,      0, sizeof(G)    );
        memset( count,  0, sizeof(count));

        int N;
        scanf( "%d",&N );
        for( int i = 0; i < N; ++i ) {
            int a, b;
            scanf( "%d %d", &a, &b );
            ++G[a][b];
            ++G[b][a];
            ++count[a];
            ++count[b];
        }

        printf( "Case #%d\n", ++cases );

        // 欧拉回路形成的条件之一，判断结点的度是否为偶数
        for( int i = 0; i < MAXN; ++i ) {
            if( count[i] & 1 ) {
                validGraph = false;
                break;
            }
        }
        // 检查图是否连通
        if( validGraph ) {
            memset( visited, 0, sizeof(visited) );
            for( int i = 0; i < MAXN; ++i ) {
                if( count[i] ) {
                    dfs(i);
                    break;
                }
            }
            for( int i = 0; i < MAXN; ++i ) {
                if( count[i] && !visited[i] ) {
                    connected = false;
                    break;
                }
            }
        }
        if( validGraph && connected ) {
            for( int i = 0; i < MAXN; ++i ) {
                if( count[i] ) {
                    euler(i);
                    break;
                }
            }
        } else {
            printf( "some beads may be lost\n" );
        }

        if( T > 0 ) { printf("\n"); }
    }
    return 0;
}

$ cat input.txt
2
5
1 2
2 3
3 4
4 5
5 6
5
2 1
2 2
3 4
3 1
2 4

$ cat input.txt | ./a.out
Case #1
some beads may be lost

Case #2
1 2
2 2
2 4
4 3
3 1

图上的宽度优先搜索 Graph BFS

最小生成树 @

构造最小生成树 (Minimum Spanning Tree, MST) 有多种算法。其中多数算法利用了最小生成树的一个性质（简称为 MST 性质）：假设 N = (V, E) 是一个连通网，U 是顶点集 V 的一个非空子集。若 (u, v) 是一条具有最小权值的边，其中 u ∈ {U}, v ∈ {V-U}，则必存在一颗包含边 (u, v) 的最小生成树。

Prim 算法和 Kruskal 算法是两个利用 MST 性质构造最小生成树的算法。它们都属于贪心法。

Prim 算法 @

假设 N = (V, E) 是一个连通网，TE 是 N 上最小生成树中边的集合。算法从 U = u₀ (u₀ ∈ V), TE = {} 开始，重复执行下述操作：在所有 u ∈ U, v ∈ V-U 的边 (u, v) ∈ E 中找一条代价最小的边 (u₀, v₀) 并入集合 TE，同时 v₀ 并入 U，直至 U = V 为止。此时 TE 中必有 n-1 条边，则 T = (V, TE) 为 N 的最小生成树。为实现这个算法需附设一个数组 closedge，以记录从 U 到 V-U 具有最小代价的边。对每个顶点 v_i ∈V-U，在辅助数组中存在一个相应分量 closedge[i-1]，它包括两个域，其中 lowcost 存储该边上的权。显然，closedge[i].lowcost = min{ cost(u, v_i), u ∈ U }。 adjvex 域存储该边依附的在 U 中的顶点。

TODO, add picture url.

+-----------------------+-----------------------+-------------------------------+-----------------------------------+
|       \               |                       |                               |                                   |
|          \       i    |                       |                               |                                   |
|             \         |   v1  v2  v3  v4  v5  |   U                           |   V-U                             |
|                \      |                       |                               |                                   |
|       closedge    \   |                       |                               |                                   |
+-----------------------+-----------------------+-------------------------------+-----------------------------------+
|       adjvex          |   v0  v0  v0          |   v0                          |   {v1, v2, v3, v4, v5}            |
|       lowcost         |   6   1   5           |                               |                                   |
|                       |       ^               |                               |                                   |
+-----------------------+-----------------------+-------------------------------+-----------------------------------+
|       adjvex          |   v2      v1  v2  v3  |   v0, v2                      |   {v1, v3, v4, v5}                |
|       lowcost         |   5   0   5   6   4   |                               |                                   |
|                       |                   ^   |                               |                                   |
+-----------------------+-----------------------+-------------------------------+-----------------------------------+
|       adjvex          |   v2      v5  v2      |   v0, v2, v5                  |   {v1,v3, v4}                     |
|       lowcost         |   5   0   2   6   0   |                               |                                   |
|                       |           ^           |                               |                                   |
+-----------------------+-----------------------+-------------------------------+-----------------------------------+
|       adjvex          |   v2          v2      |   v0, v2, v5, v3              |   {v1, v4}                        |
|       lowcost         |   5   0   0   6   0   |                               |                                   |
|                       |   ^                   |                               |                                   |
+-----------------------+-----------------------+-------------------------------+-----------------------------------+
|       adjvex          |               v1      |   v0, v2, v5, v3, v1          |   {v4}                            |
|       lowcost         |   0   0   0   3   0   |                               |                                   |
|                       |               ^       |                               |                                   |
+-----------------------+-----------------------+-------------------------------+-----------------------------------+
|       adjvex          |                       |   v0, v2, v5, v3, v1, v4      |   {}                              |
|       lowcost         |   0   0   0   0   0   |                               |                                   |
+-----------------------+-----------------------+-------------------------------+-----------------------------------+

#include <cstdio>
#include <climits>                          // INT_MAX

using namespace std;

const int MAX_NV = 100;

typedef int graph_weight_t;
const graph_weight_t GRAPH_INF = INT_MAX;

// 图，用邻接矩阵(Adjacency Matrix).
struct graph_t {
    int nv;
    int ne;
    graph_weight_t matrix[MAX_NV][MAX_NV];
};

graph_t g;

struct closedge_t {
    int adjvex;                             // 弧头，属于 U
    graph_weight_t lowcost;                 // distance: adjvex -> [cur], -GRAPH_INF 表示已经加入 U
};

// 在 V-E 集合中寻找最小的边
// closedge:    MST 中的边，起点为 adjvex，终点为本下标
// n:           closedge 数组的长度

// return:      找到了则返回弧尾的下标，V-U 为空集则返回 -1，表示终止
int min_element( const closedge_t closedge[], int n ) {
    int min_value = GRAPH_INF;
    int min_pos = -1;
    for( int i = 0; i < n; ++i )
        if( closedge[i].lowcost > -GRAPH_INF ) {            // not in U
            if( min_value > closedge[i].lowcost ) {
                min_value = closedge[i].lowcost;
                min_pos = i;
            }
        }
    return min_pos;
}

// Prim 算法，求图的最小生成树.
// return:      MST 的边的权值之和
graph_weight_t prim( const graph_t &g ) {
    graph_weight_t sum = 0;                 // 权值之和
    const int n = g.nv;
    int u = 0;                              // 从 0 号顶点出发

    // closedge[n]，记录从顶点集 U 到 V-U 的边
    closedge_t *closedge = new closedge_t[n];

    // 辅助数组初始化
    for( int i = 0; i < n; ++i ) {
        if( i == u ) { continue; }
        closedge[i].adjvex = u;
        closedge[i].lowcost = g.matrix[u][i];
    }
    closedge[u].lowcost = -GRAPH_INF;       // 初始, U = {u}

    for( int i = 0; i < n; ++i ) {
        if( i == u ) { continue; }
        // 其余的 n-1 个顶点
        // 求出 TE 的下一个顶点 k
        int k = min_element( closedge, n );
        // 输出此边 closedge[k].adjvex --> k
        printf( "%c - %c: %d\n", 'A'+closedge[k].adjvex, 'A'+k, g.matrix[closedge[k].adjvex][k] );

        sum += g.matrix[closedge[k].adjvex][k];         // sum += closedge[k].lowcost;

        closedge[k].lowcost = -GRAPH_INF;               // 顶点 k 并入 U，表示此边加入 TE
        for( int j = 0; j < n; ++j ) {                  // 更新 k 的邻接点的值
            const graph_weight_t &w = g.matrix[k][j];
            if( w < closedge[j].lowcost ) {
                closedge[j].adjvex  = k;
                closedge[j].lowcost = w;
            }
        }
    }
    delete[] closedge;
    return sum;
}

// 读取输入，构建图.
void read_graph() {
    int m, n;
    scanf( "%d %d", &m, &n );               // #vertex, #edge
    g.nv = m;
    g.ne = n;

    // 初始化图，所有节点间距离为无穷大
    for( int i = 0; i < m; ++i ) {
        for( int j = 0; j < m; ++j ) {
            g.matrix[i][j] = GRAPH_INF;
        }
    }

    // 读取边信息
    for( int k = 0; k < n; ++k ) {
        char chx[5], chy[5];
        int w;
        scanf( "%s %s %d", chx, chy, &w );
        int i = chx[0] - 'A';
        int j = chy[0] - 'A';
        g.matrix[i][j] = w;
        g.matrix[j][i] = w;
    }
}

int main() {
    read_graph();
    printf( "Total: %d\n", prim(g) );
    return 0;
}

$ cat input.txt
7 11
A B 7
A D 5
B C 8
B D 9
B E 7
C E 5
D E 15
D F 6
E F 8
E G 9
F G 11

$ cat input.txt | ./tmp
A - D: 5
D - F: 6
A - B: 7
B - E: 7
E - C: 5
E - G: 9
Total: 39

算法分析

假设网中有 n 个顶点，则第一个进行初始化的循环语句的频度为 n，第二个循环语句的频度为 n-1。其中有两个内循环：其一是在 closedge[v].lowcost 中求最小值，其频度为 n-1；其二是重新选择具有最小代价的边，其频度为 n。因此 Prim 算法的时间复杂度为 O(n²)，与网中边数无关，因此适用于求边稠密的图的最小生成树。

Prim 算法的另一种实现是使用小根堆，其流程是：小根堆中存储一个端点在生成树中，另一个端点不在生成树的边，每次从小根堆的堆顶可选出权值最小的边 (u, v)，将其从堆中推出，加入生成树中。然后将新出现的所有一个端点在生成树中，一个端点不在生成树的边都插入小根堆中。下一轮迭代中，下一条满足要求的边又上升到堆顶。如此重复 n-1 次，最后建立起该图的最小生成树。该算法的C 代码实现如下。

```cpp #include #include // INT_MAX #include #include #include

using namespace std;

const int MAX_NV = 100;

typedef int graph_weight_t; const graph_weight_t GRAPH_INF = INT_MAX;

// 图，用邻接矩阵 (Adjacency Matrix). struct graph_t { int nv; int ne; graph_weight_t matrix[MAX_NV][MAX_NV]; };

graph_t g;

// 边 struct edge_t { int u; // from int v; // to graph_weight_t w; // 权值 bool operator>( const edge_t &other ) const { return w > other.w; } };

// Prim 算法，求图的最小生成树. // return: MST 的边的权值之和 int prim( const graph_t &g ){ graph_weight_t sum = 0; // 权值之和 priority_queue<edge_t, vector, greater > pq; const int n = g.nv; vector used( n, 0 ); // 判断顶点是否已经加入最小生成树

char strncpy(char dest, const char *src, size_t n) { size_t i;

   for (i = 0; i < n && src[i] != '\0'; i++)
       dest[i] = src[i];
   for ( ; i < n; i++)
       dest[i] = '\0';

   return dest;

} int u = 0; // 从 0 号顶点出发 used[u] = 1; int count = 1; // MLE 当前的边数

                // 开始顶点加入 U (所以 count 初始为 1)
                while( count < n ) {
                    for( int v = 0; v < n; ++v ) {
                        if( !used[v] ) {
                            edge_t e = {u, v, g.matrix[u][v]};  // 若 v 不在生成树，(u,v) 加入堆
                            pq.push(e);
                        }
                    }
                    while( !pq.empty() && count < n ) {
                        edge_t e = pq.top(); pq.pop();          // 从堆中退出最小权值边，存入 e
                        if( used[e.v] ) { continue; }

                        printf( "%c - %c: %d\n", 'A'+e.u, 'A'+e.v, g.matrix[e.u][e.v] );
                        sum += g.matrix[e.u][e.v];
                        u = e.v;
                        used[u] = 1;                            // u 并入到生成树的顶点集合 U
                        ++count;
                        break;

                    }
                }

                return sum;
            }

            // 读取输入，构建图.
            void read_graph() {
                int m, n;
                scanf( "%d %d", &m, &n );                       // #vertex, #edge
                g.nv = m;
                g.ne = n;

                // 初始化图，所有节点间距离为无穷大
                for( int i = 0; i < m; ++i ) {
                    for( int j = 0; j < m; ++j ) {
                        g.matrix[i][j] = GRAPH_INF;
                    }
                }

                // 读取边信息
                for( int k = 0; k < n; ++k ) {
                    char chx[5], chy[5];
                    int w;
                    scanf( "%s %s %d", chx, chy, &w );
                    int i = chx[0] - 'A';
                    int j = chy[0] - 'A';
                    g.matrix[i][j] = w;
                    g.matrix[j][i] = w;
                }
            }

            int main() {
                read_graph();
                printf( "Total: %d\n", prim(g) );
                return 0;
            }
            ```

            该算法迭代次数为 O(n)，每次迭代将平均 e/n 条边插入最小
            堆中，e 条边从堆中删除，堆的插入和删除操作时间复杂度均
            为 O(log~2~e)，则总的时间复杂度为 O(e*log~2~e)。

    -   Kruskal 算法 `@`{.fold}

        :   假设连通网 N = {V, E}，则令最小生成树的初始状态为只有 n
            个顶点而无边的非连通图 T = (V, {})，图中每个顶点自成一
            个连通分量。在 E 中选择代价最小的边，若该边依附的顶点落
            在 T 中不同的连通分量上，则将此边加入到 T 中，否则舍去此
            边而选择下一条代价最小的边。依次类推，直至 T 中所有顶点
            都在同一连通分量上为止。

            ```cpp
            #include <iostream>
            #include <queue>
            #include <algorithm>
            #include <stdlib.h>

            using namespace std;

            struct edge_t{
                int u, v, w;
                bool operator>( const edge_t &other ) const {
                    return w > other.w;
                }
            };

            const int MAX_NV = 11;
            const int MAX_NE = 100;
            edge_t edges[MAX_NE];

            // union-find set
            struct UFS {
                explicit UFS( int n ) { arr = vector<int>(n, -1); }
                int Find( int idx ) {
                    int oldidx = idx;
                    while( arr[idx] >= 0 ) { idx = arr[idx]; }
                    while( oldidx != idx ) {
                        int next = arr[oldidx];
                        arr[oldidx] = idx;
                        oldidx = next;
                    }
                    return idx;
                }
                void Union( int a, int b ) {
                    int ra = Find(a), rb = Find(b);
                    if( ra == rb ) { return; }
                    arr[ra] += arr[rb];
                    arr[rb] = ra;
                }
                int Size( int a ) { return -arr[Find(a)]; }
                vector<int> arr;
            };

            // Kruskal 算法，堆 + 并查集.
            // edges:       边的数组
            // n:           边数，一定要大于或等于 (顶点数 -1)
            // m:           顶点数
            // return:      MST的边的权值之和
            int kruskal( const edge_t edges[], int n, int m ) {
                if( n < m - 1 ) { return -1; }
                int sum = 0;
                priority_queue<edge_t, vector<edge_t>, greater<edge_t> > pq;
                // 把所有边插入堆中
                for( int i = 0; i < n; ++i ) {
                    pq.push( edges[i] );
                }
                UFS ufs( MAX_NV );
                for( int i = 0; i < n; ++i ) {
                    edge_t e = pq.top(); pq.pop();      // 从堆中退出最小权值边
                    // 取两顶点所在集合的根
                    int u = ufs.Find( e.u );
                    int v = ufs.Find( e.v );
                    if( u != v ) {                      // 不是同一集合，说明不连通
                        ufs.Union( u, v );              // 合并，连通成一个分量
                        // 输出生成树 TE 的边，即此边加入 TE
                        printf( "%c - %c: %d\n", 'A'+e.u, 'A'+e.v, e.w );
                        sum += e.w;
                    }
                }
                return sum;
            }

            int main() {
                int m, n;
                scanf( "%d %d", &m, &n );                       // #vertex, #edge
                for (int i = 0; i < n; i++) {                   // 读取边信息
                    char chx[5], chy[5];
                    int w;
                    scanf( "%s %s %d", chx, chy, &w );
                    int u = chx[0] - 'A';
                    int v = chy[0] - 'A';
                    edges[i].u = u;
                    edges[i].v = v;
                    edges[i].w = w;
                }
                // 求解最小生成树
                printf( "Total: %d\n", kruskal(edges, n, m) );
                return 0;
            }
            ```

            sort + union-find set

            :   ```cpp
                // for std::sort
                bool operator<( const edge_t &e1, const edge_t &e2 ) {
                    return e1.w < e2.w;
                }

                // Kruskal 算法，快排 + 并查集
                int kruskal2( edge_t edges[], int n, int m ) {
                    if( n < m - 1) { return -1; }
                    int sum = 0;
                    std::sort( edges, edges + n );
                    UFS ufs( MAX_NV );
                    for( int i = 0; i < n; ++i ) {
                        edge_t &e = edges[i];
                        int u = ufs.Find( e.u );
                        int v = ufs.Find( e.v );
                        if( u != v ) {
                            ufs.Union( u, v );
                            printf( "%c - %c: %d\n", 'A'+e.u, 'A'+e.v, e.w );
                            sum += e.w;
                        }
                    }
                    return sum;
                }
                ```

                如果采用邻接矩阵作为图的存储结构，则在建立小根堆时
                需要检测图的邻接矩阵，这需要 O(n^2^) 的时间。此外，
                需要将 e 条边组成初始的小根堆。如果直接从空堆开始，
                依次插入各边，需要 O(e*log~2~e) 的时间。在构造最小
                生成树的过程中，需要进行 O(e) 次出堆操作
                `heap_remove()`、2e 次并查集的 `ufs.Find()` 操作以
                及 n-1 次`ufs.Union()` 操作，计算时间分别为
                O(e*log~2~e)、O(log~2~n) 和 O(n)，所以总时间为
                O(n^2^+e*log~2~e)。

                如果采用邻接表作为图的存储结构，则在建立小根堆时需
                要检测图的邻接表，这需要 O(n+e) 的时间。为建成初始
                的小根堆，需要 O(e*log~2~e) 的时间。在构造最小生成
                树的过程中，需要进行 O(e) 次出堆操作`heap_remove()`
                、2e 次并查集的 `ufs.Find()` 操作以及 n-1 次
                `ufs.Union()` 操作，计算时间分别为 O(e*log~2~e)、
                O(e*log~2~n) 和 O(n)，所以总时间为 O(n+e*log~2~e)。

    -   Highways `@`{.fold}

        :   一个名叫 Flatopia 的岛国地势非常平坦。不幸的是 Flatopia
            的公共高速公路系统很差劲。Flatopia 的政府也意识到了这个
            问题，已经建造了许多高速公路用来连接比较重要的城镇。不
            过，仍然有一些城镇没有接入高速公路。因此，很有必要建造
            更多的高速公路，让任意两个城镇之间可以通过高速公路连接。

            Flatopia 的城镇从 1 到 N 编号，城镇 i 的位置由笛卡尔坐
            标 (x~i~, y~i~) 表示。每条高速公路仅连接两个城镇。所有
            的高速公路都是直线，因此它们的长度就等于两个城镇之间的
            欧氏距离。所有的高速公路是双向的，高速公路之间可以相交，
            但是司机只能在公路的端点（也即城镇）换道。

            Flatopia 政府希望能最小化建造高速公路的代价。由于
            Flatopia 地势平坦，一条高速公路的代价正比于它的长度。因
            此，应该让高速公路的总长度最小。

            ```
            输入

                输入由两部分组成。
                第一部分描述所有的城镇，
                第二部分描述所有已经建造好的高速公路。

                第一行包含一个整数 N (1 <= N <= 750)，表示城镇的数目。
                接下来的 N 行每行包含一对整数，x_i 和 y_i，由空格隔开，
                表示第 i 个城镇的坐标。坐标的绝对值不会超过 10000。
                每个城镇的坐标都不重叠。

                接下来一行包含一个整数 M (0 <= M <= 1000)，表示已经存在的高速公路的数目。
                接下来的 M 行每行包含一对整数，给出了一对城镇编号，表示这两个城镇被一条高速公路连接起来。
                每两个城镇之间最多被一条高速公路连接。

                9
                1 5
                0 0
                3 2
                4 5
                5 1
                0 4
                5 2
                1 2
                5 3
                3
                1 3
                9 7
                1 2

            输出

                输出所有需要新建的高速公路。每行一个高速公路，用一对城镇编号表示。
                如果不需要新建高速公路，输出为空。

                1 6
                3 7
                4 9
                5 7
                8 3
            ```

            很明显，最小生成树。

            **题中的网络是一个完全图，任意两个城镇之间都有边，权值是
            两点间的距离。因此 Prim 算法比 Kruskal 算法效率更高。**

            对于已经存在的高速公路，令它们权值为 0，可以保证它们一定会被选中。

            因为题目只需要输出新建的高速公路的两个端点，不需要输出
            最小生成树的长度，所以计算距离的时候不用 sqrt，也就不用 double 了。

            ```cpp
            #include <cstdio>
            #include <queue>
            #include <vector>

            using namespace std;

            const int MAX_NV = 750;
            int n, m, x[MAX_NV], y[MAX_NV];

            struct graph_t {
                int nv, ne;
                int matrix[MAX_NV][MAX_NV];
            };
            graph_t g;

            struct edge_t {
                int u, v, w;
                bool operator>( const edge_t &other ) const { return w > other.w; }
            };

            int u;                                              // 从 u 号顶点出发

            void prim( const graph_t &g ){
                priority_queue<edge_t, vector<edge_t>, greater<edge_t> > pq;
                const int n = g.nv;
                vector<int> used( n, 0 );                       // 判断顶点是否已经加入最小生成树

                used[u] = 1;
                int count = 1;                                  // MLE 当前的边数

                // 开始顶点加入 U (所以 count 初始为 1)
                while( count < n ) {
                    for( int v = 0; v < n; ++v ) {
                        if( !used[v] ) {
                            edge_t e = {u, v, g.matrix[u][v]};  // 若 v 不在生成树，(u,v) 加入堆
                            pq.push(e);
                        }
                    }
                    while( !pq.empty() && count < n ) {
                        edge_t e = pq.top(); pq.pop();          // 从堆中退出最小权值边，存入 e
                        if( used[e.v] ) { continue; }
                        if( g.matrix[e.u][e.v] > 0 ) {
                            printf( "%d %d\n", e.u+1, e.v+1 );
                        }
                        used[u=e.v] = 1;                        // u 并入到生成树的顶点集合 U
                        ++count;
                        break;
                    }
                }
            }

            int main() {
                // 读取输入，构建图.
                scanf( "%d", &n );
                g.nv = n;
                g.ne = n*(n-1)/2;
                for( int i = 0; i < n; ++i ) { scanf( "%d %d", &x[i], &y[i] ); }
                for( int i = 0; i < n; ++i ) {
                    for( int j = 0; j < n; ++j  ) {
                        g.matrix[i][j] = g.matrix[j][i] = (x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]);
                    }
                }
                scanf( "%d", &m );
                for( int i = 0; i < m; ++i ) {
                    int a, b;
                    scanf( "%d %d", &a, &b );
                    g.matrix[a-1][b-1] = g.matrix[b-1][a-1] = 0;
                    u = a;
                }

                prim( g );
                return 0;
            }
            ```

            我的输出为:

            ```
            1 6
            3 7
            7 5
            3 8
            9 4
            ```

            顺序不一样, 但是城市是一样的.

    -   最优布线问题 `@`{.fold}

        :   学校需要将 n 台计算机连接起来，不同的 2 台计算机之间的
            连接费用可能是不同的。为了节省费用，我们考虑采用间接数
            据传输结束，就是一台计算机可以间接地通过其他计算机实现
            和另外一台计算机连接。

            为了使得任意两台计算机之间都是连通的（不管是直接还是间
            接的），需要在若干台计算机之间用网线直接连接，现在想使
            得总的连接费用最省，让你编程计算这个最小的费用。

            ```
            输入

                输入第一行为两个整数 n,m (2 <= n <= 100000, 2 <= m <= 100000)，
                表示计算机总数，和可以互相建立连接的连接个数。接下
                来 m 行，每行三个整数 a,b,c 表示在机器 a 和机器 b
                之间建立连接的话费是 c。(题目保证一定存在可行的连通
                方案, 数据中可能存在权值不一样的重边，但是保证没有
                自环)

                3 3
                1 2 1
                1 3 2
                2 3 1

            输出

                输出只有一行一个整数，表示最省的总连接费用。

                2
            ```

            本题是非常直白的 kruskal 算法，可以直接使用 kruskal 节的样例代码。

            ```cpp
            #include <cstdio>
            #include <queue>

            using namespace std;

            struct edge_t {
                int u, v, w;
                bool operator>( const edge_t &other ) const { return w > other.w; }
            };
            const int MAX_NV = 100001;
            const int MAX_NE = 100000;
            edge_t edges[MAX_NE];

            struct UFS {
                explicit UFS( int n ) { arr = vector<int>(n, -1); }
                int Find( int idx ) {
                    int oldidx = idx;
                    while( arr[idx] >= 0 ) { idx = arr[idx]; }
                    while( oldidx != idx ) {
                        int next = arr[oldidx];
                        arr[oldidx] = idx;
                        oldidx = next;
                    }
                    return idx;
                }
                void Union( int a, int b ) {
                    int ra = Find(a), rb = Find(b);
                    if( ra == rb ) { return; }
                    arr[ra] += arr[rb];
                    arr[rb] = ra;
                }
                int Size( int a ) { return -arr[Find(a)]; }
                vector<int> arr;
            };

            long long kruskal( const edge_t edges[], int n, int m ) {
                if( n < m - 1 ) { return -1; }
                long long sum = 0LL;
                priority_queue<edge_t, vector<edge_t>, greater<edge_t> > pq;
                for( int i = 0; i < n; ++i ) { pq.push( edges[i] ); }
                UFS ufs( MAX_NV );
                for( int i = 0; i < n; ++i ) {
                    edge_t e = pq.top(); pq.pop();
                    int u = ufs.Find( e.u );
                    int v = ufs.Find( e.v );
                    if( u != v ) {
                        ufs.Union( u, v );
                        sum += e.w;
                    }
                }
                return sum;
            }

            int main() {
                int n, m;
                scanf( "%d %d", &n, &m );
                for( int i = 0; i < m; ++i ) {
                    scanf( "%d %d %d", &edges[i].u, &edges[i].v, &edges[i].w );
                }
                printf( "%lld\n", kruskal(edges, n, m) );
                return 0;
            }
            ```

最短路径 ♥️ @

单源最短路径 — Dijkstra 算法 @

假设 S 为已求得最短路径的点的集合，则可证明：下一条最短路径（设其终点为 x）或者是弧 (v, x)，或者是中间只经过 S 中的顶点而最后到达顶点 x 的路径。

Dijkstra 算法流程如下：

S 为已找到从 v 出发的最短路径的终点的集合，它的初始状态为空集。dist[i] 存放的是 v 到 v_i 的最短路径长度，根据前面所述性质，

dist[i] = min{ dist[i], weight(v, v_i) }。

path[i] 存放的是最短路径上指向 v_i 的弧尾顶点。那么从 v 出发到图上其余 v_i 的最短路径长度的初值为：

dist[i] = weight(v, v_i), v_i ∈ V
选择 v_j，使得

dist[j] = min{ dist[j], weight(v, v_j) | v_j ∈ V-S };

将 v_j 加入到 S，

S = S ∪ v_j
修改从 v 出发到集合 V-S 上任一顶点 v_k 可达的最短路径长度，并记录下这条边。
```
if( dist[j] + weight(j,k) < dist[k] ) {
    dist[k] = dist[j] + weight(j,k);
    path[k] = j;
}
```
重复 2，3 共 n-1 次。

TODO, add pic url.

End Point           i=1         i=2         i=3         i=4         i=5
-----------------------------------------------------------------------
    v1              inf         inf         inf         inf         inf
-----------------------------------------------------------------------
    v2              10
                 (v0,v2)
-----------------------------------------------------------------------
    v3              inf         60          50
                            (v0,v2,v3)  (v0,v4,v5)
-----------------------------------------------------------------------
    v4              30          30
                 (v0,v4)     (v0,v4)
-----------------------------------------------------------------------
    v5             100         100          90          60
                 (v0,v5)     (v0,v5)    (v0,v4,v5)  (v0,v4,v3,v5)
-----------------------------------------------------------------------
    vj              v2          v4          v3          v5
    S            (v0,v2)    (v0,v2,v4)  (v0,v2,v3,v4)   (v0,v2,v3,v4,v5)

#include <iostream>
#include <queue>
#include <map>
#include <utility>
#include <climits>

using namespace std;

// 图，用邻接表 (Adjacency List).
struct graph_t {
    int nv, ne;
    map<char, map<char, int> > matrix;
};

// Dijkstra 算法求单源最短路径.
// g:           图
// start:       起点
// dist:        dist[v] 存放的是起点到 v 的最短路径长度
// father:      father[v] 存放的是最短路径上指向 v 的上一个顶点
void dijkstra( const graph_t &g, char start, map<char, int> &distance, map<char, char> &father ) {
    typedef pair<int, char> to_dist_t;
    priority_queue<to_dist_t, vector<to_dist_t>, greater<to_dist_t> > pq;
    pq.push( to_dist_t( distance[start]=0, start ) );
    while( !pq.empty() ) {
        to_dist_t u = pq.top(); pq.pop();
        char &vj = u.second;
        if( !g.matrix.count(vj) ) { continue; }
        for( auto const p : g.matrix.at(vj) ) {
            const char &vk  = p.first;
            const int  &wjk = p.second;
            //    vk not in S       or    there's a shorter path to vk
            if( !distance.count(vk) || distance[vj] + wjk < distance[vk] ) {
                distance[ vk  ]     =  distance[vj] + wjk;
                father[   vk  ]     =  vj;
                pq.push( to_dist_t(distance[vk], vk) );
            }
        }
    }
}

void print_path( const map<char, char> &father, char end ) {
    if( !father.count(end) ) {
        printf( "%c", end );
    } else {
        print_path( father, father.at(end) );
        printf( "->%c", end );
    }
}

int main() {
    graph_t g;

    scanf( "%d", &g.ne );
    for( int i = 0; i < g.ne; ++i ) {
        char u[5], v[5];
        int w;
        scanf( "%s %s %d", u, v, &w );
        g.matrix[*u][*v] = w;
    }

    map<char, int> distance;
    map<char, char> father;
    dijkstra( g, 'A', distance, father );

    for( const auto p : father ) {
        if( p.first != 'A' ) {
            print_path( father, p.first );
            printf( "\n" );
        }
    }
    return 0;
}

$ cat input.txt
8
A C 10
A E 30
A F 100
B C 5
C D 50
D F 10
E D 20
E F 60

$ cat input.txt | ./tmp
A->C
A->E->D
A->E
A->E->D->F

算法分析: 该算法包含了两个并列的 for 循环，第一个 for 循环做辅助数组的初始化工作，计算时间为 O(n)，第二个 for 循环是二重嵌套循环，进行最短路径的求解工作，由于对图中几乎每个顶点都要做计算，每个顶点的又要对集合 S 内的顶点进行检测，对集合 V-S 内中的顶点进行修改，所以运算时间复杂度为 O(n²)。算法总的时间复杂度为 O(n²)。

每点最短路径 — Floyd 算法 @

shit @

\subsection{每点最短路径——Floyd算法}
Floyd算法的基本思想是：假设求从定点$v_i$到$v_j$的最短路
径。初始时，若$v_i$与$v_j$之间存在边，则最短路径长度为
此边的权值；若不存在边，则最短路径长度为无穷大。以后逐
步在路径中加入顶点$k(k=0,1,...,n-1)$作为中间顶点，如果
加入中间顶点后，得到的路径比原来的路径长度减少了，则以
新路径代替原路径。

首先比较$(v_i,v_j)$和$(v_i,v_0,v_j)$的路径长度，取较短
者为从$v_i$到$v_j$的中间顶点的序号不大于0的最短路径。如
果$(v_i,v_0,v_j)$较短，则取$(v_i,v_0,v_j)$作为最短路径
。假如在路径上再增加一个顶点$v_1$，也就是说，如果
$(v_i,...,v_1)$和$(v_1,...,v_j)$分别是当前找到的中间定
点的序号不大于0的最短路径，那么$(vi,...,v1,...,vj)$就有
可能是从$v_i$到$v_j$的中间顶点的序号不大于1的最短路径，
将它和已经得到的从$v_i$到$v_j$的中间顶点的序号不大于0的
最短路径相比较，选出较短者作为从$v_i$到$v_j$的中间顶点
的序号不大于1的最短路径。再增加一个顶点$v_2$，继续进行
试探，依此类推。一般的，若$(v_i,...,v_k)$和
$(v_k,...,v_j)$分别是从$v_i$到$v_k$和从$v_k$到$v_j$的中
间定点的序号不大于$k-1$的最短路径，则将
$(v_i,...,v_k,...,v_j)$和已经得到的从$v_i$到$v_j$的中间
顶点的序号不大于$k-1$的最短路径相比，较短者便是从$v_i$
到$v_j$的中间顶点的序号不大于$k$的最短路径。这样，在经
过$n$次比较后，最后求得的必是从$v_i$到$v_j$的最短路径。

现定义一个$n$阶方阵序列，
$$
D^{(-1)}, D^{(0)} , D^{(1)},..., , D^{(k)},..., , D^{(n-1)}
$$
其中，
\begin{eqnarray}
D^{(-1)}[i][j] &=& \text{g->matrix}[i][j],  \nonumber \\
D^{(k)}[i][j] &=& \min\left\{D^{(k-1)}[i][j], D^{(k-1)}[i][k] + D^{(k-1)}[k][j]\right\},0 \leq k \leq n-1 \nonumber
\end{eqnarray}

上述公式中，$D^{(k)}[i][j]$是从$v_i$到$v_j$的中间顶点的序号不大于$k$的最短路径的长度；$D^{(n-1)}[i][j]$是从$v_i$到$v_j$的最短路径的长度。

例如，对图\ref{fig:floyd}所示的有向图及其邻接矩阵运行Floyd算法，

\begin{center}
\includegraphics[width=180pt]{floyd.png}\\
\figcaption{有向图及其邻接矩阵}\label{fig:floyd}
\end{center}

运算过程中矩阵D的变化如表\ref{tab:floyd}所示。

\begin{center}
\tabcaption{Floyd算法过程中方阵和最短路径的变化}
\label{tab:floyd}
\begin{tabular}{|c|ccc|ccc|ccc|ccc|}
\hline
\multirow{2}{*}{$\mathbf{D}$} &
\multicolumn{3}{|c|}{$\mathbf{D^{(0)}}$} &
\multicolumn{3}{|c|}{$\mathbf{D^{(1)}}$} &
\multicolumn{3}{|c|}{$\mathbf{D^{(2)}}$} &
\multicolumn{3}{|c|}{$\mathbf{D^{(3)}}$} \\
 & 0 & 1 & 2 & 0 & 1 & 2 & 0 & 1 & 2 & 0 & 1 & 2 \\
\hline
0 & 0 & 4 & 11 & 0 & 4 & 11 & 0 & 4 & 6 & 0 & 4 & 6 \\
1 & 6 & 0 & 2 & 6 & 0 & 2 & 6 & 0 & 2 & 5 & 0 & 2 \\
2 & 3 & $\infty$ & 0 & 3 & 7 & 0 & 3 & 7 & 0 & 3 & 7 & 0 \\
\hline
\multirow{2}{*}{$\mathbf{P}$} &
\multicolumn{3}{|c|}{$\mathbf{P^{(0)}}$} &
\multicolumn{3}{|c|}{$\mathbf{P^{(1)}}$} &
\multicolumn{3}{|c|}{$\mathbf{P^{(2)}}$} &
\multicolumn{3}{|c|}{$\mathbf{P^{(3)}}$} \\
 & 0 & 1 & 2 & 0 & 1 & 2 & 0 & 1 & 2 & 0 & 1 & 2 \\
\hline
\multirow{2}{*}{0} & & A & A & & AB & A & & AB & AB & & AB & AB \\
                   & & B & C & & & C & & & C & & & C \\
\hline
\multirow{2}{*}{1} & B & & B & B & & B & B & & BC & BC & & BC \\
                   & A & & C & A & & C & A & & & A & & \\
\hline
\multirow{2}{*}{2} & C & & & C & CA & & C & CA & & CA & CA & \\
                   & A & & & A & B & & A & B & & & B & \\
\hline
\end{tabular}
\end{center}

Floyd 算法的 C 语言实现 @

#include <iostream>
#include <climits>

using namespace std;

const int MAX_NV = 100;
const int GRAPH_INF = INT_MAX / 2;              // 确保加法不溢出

struct graph_t {
    int nv, ne;
    int matrix[MAX_NV][MAX_NV];
};

graph_t g;

int dist[MAX_NV][MAX_NV];                       // dist[i][j] 是顶点 i 和 j 之间最短路径长度
int path[MAX_NV][MAX_NV];                       // path[i][j] 是最短路径上 i 和 j 之间的顶点

// Floyd 算法求每点之间最短路径.
// dist:        dist[i][j] 是顶点 i 和 j 之间最短路径长度
// path:        path[i][j] 是最短路径上 i 和 j 之间的顶点
void floyd( const graph_t &g, int dist[][MAX_NV], int path[][MAX_NV] ) {
    const int n = g.nv;
    for( int i = 0; i < n; ++i ) {
        for( int j = 0; j < n; ++j ) {
            if( i != j ) {
                dist[i][j] = g.matrix[i][j];
                path[i][j] = i;
            } else {
                dist[i][j] =  0;
                path[i][j] = -1;
            }
        }
    }
    for( int k = 0; k < n; ++k ) {
        for( int i = 0; i < n; ++i ) {
            for( int j = 0; j < n; ++j ) {
                // i 到 j 的路径上加入顶点 k 可以缩短路径长度
                if( dist[i][k] + dist[k][j] < dist[i][j] ) {
                    dist[i][j] = dist[i][k] + dist[k][j];
                    path[i][j] = k;
                }
            }
        }
    }
}

// 打印从 u 到 v 的最短路径
static void print_path_r( int u, int v, const int path[][MAX_NV] ) {
    if( path[u][v] == -1 ) {
        printf( "%c", 'A'+u );
    } else {
        print_path_r( u, path[u][v], path );
        printf( "->%c", 'A'+v );
    }
}

// 打印 u 到其他所有点的最短路径
void print_path( const graph_t &g, const int path[][MAX_NV] ) {
    for( int i = 0; i < g.nv; ++i ) {
        for( int j = 0; j < g.nv; ++j ) {
            if( i != j ) {
                print_path_r( i, j, path );
                printf( "\n" );
            }
        }
        printf( "\n" );
    }
}

int main() {
    scanf( "%d %d", &g.nv, &g.ne );
    for( int i = 0; i < g.nv; ++i ) {
        for( int j = 0; j < g.nv; ++j ) {
            g.matrix[i][j] = GRAPH_INF;
        }
    }
    for( int k = 0; k < g.ne; ++k ) {
        char chx[5], chy[5];
        int w;
        scanf( "%s %s %d", chx, chy, &w );
        g.matrix[*chx-'A'][*chy-'A'] = w;
    }

    floyd( g, dist, path );
    print_path( g, path  );
    return 0;
}

input:

    3 5
    A B 4
    A C 11
    B A 6
    B C 2
    C A 3

output:

    A->B
    A->B->C

    B->C->A
    B->C

    C->A
    C->A->B

算法分析 @

该算法中有两个并列的 for 循环，第一个循环是个二重循环，用于初始化方阵 D；第二个循环是个三重循环，逐步生成 D⁽⁰⁾, D⁽¹⁾, …, D^(n-1)。所以算法总的时间复杂度为 O(n³)。

Dijkstra 算法权值不能为负，Floyd 权值可以为负，但环路之和不能为负。

HDU 2544 最短路 @

在每年的校赛里，所有进入决赛的同学都会获得一件很漂亮的 t-shirt。但是每当我们的工作人员把上百件的衣服从商店运回到赛场的时候，却是非常累的！所以现在他们想要寻找最短的从商店到赛场的路线，你可以帮助他们吗？

输入

    输入包括多组数据。每组数据第一行是两个整数 N, M (N <= 100, M <= 10000)，
    N 表示成都的大街上有几个路口，标号为 1 的路口是商店所在地，标号为 N 的路口是赛场所在地，
    M 则表示在成都有几条路。N=M=0 表示输入结束。
    接下来 M 行，每行包括 3 个整数 A,B,C (1 <= A,B <= N, 1 <= C <= 1000),
    表示在路口 A 与路口 B 之间有一条路，我们的工作人员需要 C 分钟的时间走过这条路。

    输入保证至少存在 1 条商店到赛场的路线。

    2 1
    1 2 3
    3 3
    1 2 5
    2 3 5
    3 1 2
    0 0

输出

    对于每组输入，输出一行，表示工作人员从商店走到赛场的最短时间

    3
    2

单源最短路径，用 Dijkstra 算法，将 dijkstra 节中的代码稍加修改即可。

注意，街道是双向的，所以给边赋值时要对称赋值。

#include <cstdio>
#include <queue>
#include <map>

using namespace std;

struct graph_t {
    int nv, ne;
    map<int, map<int, int> > matrix;
};

void dijkstra( const graph_t &g, int start, map<int, int> &distance, map<int, int> &father ) {
    typedef pair<int, int> to_dist_t;
    priority_queue<to_dist_t, vector<to_dist_t>, greater<to_dist_t> > pq;
    pq.push( to_dist_t( distance[start]=0, start ) );
    while( !pq.empty() ) {
        to_dist_t u = pq.top(); pq.pop();
        int &vj = u.second;
        if( !g.matrix.count(vj) ) { continue; }
        for( auto const p : g.matrix.at(vj) ) {
            const int  &vk  = p.first;
            const int  &wjk = p.second;
            //    vk not in S       or    there's a shorter path to vk
            if( !distance.count(vk) || distance[vj] + wjk < distance[vk] ) {
                distance[ vk  ]     =  distance[vj] + wjk;
                father[   vk  ]     =  vj;
                pq.push( to_dist_t(distance[vk], vk) );
            }
        }
    }
}

void print_path( const map<int, int> &father, int end ) {
    if( !father.count(end) ) {
        printf( "%c", end );
    } else {
        print_path( father, father.at(end) );
        printf( "->%c", end );
    }
}

int main() {
    graph_t g;
    while( 2 == scanf( "%d %d", &g.nv, &g.ne ) && g.nv && g.ne ) {
        for( int i = 0; i < g.ne; ++i ) {
            int u, v, w;
            scanf( "%d %d %d", &u, &v, &w );
            g.matrix[u][v] = g.matrix[v][u] = w;
        }
        map<int, int> distance;
        map<int, int> father;
        dijkstra( g, 1, distance, father );
        printf( "%d\n", distance[g.nv]   );
    }
    return 0;
}

POJ 1125 Stockbroker Grapevine :TODO: @

TODO

拓扑排序 @

由某个集合上的一个偏序得到该集合上的一个全序，这个操作称为拓扑排序。

拓扑序列的特点是：若有向边 (V_i, V_j) 是途中的弧，则在序列中顶点 V_i 必须排在顶点 V_j 之前。

如果用有向图表示一个工程，顶点表示活动，用有向边 (V_i, V_j) 表示活动必须先于活动进行。这种有向图叫做顶点表示活动的网络 (Activity On Vertext Network)，简称 AOV 网络。

检测 AOV 网络是否存在环的方法是对 AOV 网络构造其顶点的拓扑有序序列。拓扑排序的基本步骤是：

在有向图中选一个没有前驱的顶点且输出之；
从图中删除该顶点和所有以它为端点的弧线。

重复以上两步，直至 1) 全部顶点输出，或 2) 当前图中不存在无前驱的顶点（这种情况说明图中存在环）。

C++ code @

#include <iostream>
#include <climits>
#include <stack>
#include <vector>

using namespace std;

const int MAX_NV = 100;
const int GRAPH_INF = INT_MAX;

struct graph_t {
    int nv, ne;
    int matrix[MAX_NV][MAX_NV];
};

graph_t g;

int topological[MAX_NV];                        // 拓扑排序的结果

// 拓扑排序.
// 无环返回 true，有环返回 false
bool topo_sort( const graph_t &g, int topological[] ) {
    const int n = g.nv;
    vector<int> in_degree( n, 0 );              // in_degree[i] 是顶点 i 的入度
    for( int i = 0; i < n; ++i ) {
        for( int j = 0; j < n; ++j ) {
            if( g.matrix[i][j] < GRAPH_INF ) { ++in_degree[j]; }
        }
    }

    stack<int> s;
    for( int i = 0; i < n; ++i ) {
        if( !in_degree[i] ) { s.push(i); }
    }

    int count = 0;                              // 拓扑序列的元素个数
    while( !s.empty() ) {
        int u = s.top(); s.pop();
        topological[count++] = u;
        for( int i = 0; i < n; ++i ) {
            if( g.matrix[u][i] < GRAPH_INF ) {
                if( --in_degree[i] == 0 ) { s.push(i); }
            }
        }
    }

    if( count != n ) {                          // 有环
        return false;
    } else {                                    // 无环
        return true;
    }
}

int main() {
    scanf( "%d %d", &g.nv, &g.ne );
    // 初始化图，所有节点间距离为无穷大
    for( int i = 0; i < g.nv; ++i ) {
        for( int j = 0; j < g.nv; ++j ) {
            g.matrix[i][j] = GRAPH_INF;
        }
    }
    // 读取边信息
    for( int k = 0; k < g.ne; ++k ) {
        char chx[5], chy[5];
        int w;
        scanf( "%s %s %d", chx, chy, &w );
        g.matrix[*chx-'A'][*chy-'A'] = w;
    }

    topo_sort( g, topological );
    for( int i = 0; i < g.nv; ++i ) {
        printf( "%c ", 'A'+topological[i] );
    }
    printf( "\n" );
    return 0;
}

input:

    6 8
    A C 10
    A E 30
    A F 100
    B C 5
    C D 50
    D 5 10
    E D 20
    E F 60

output:

    B A E F C D

对有 n 个顶点和 e 条边的 AOV 网络而言，求各顶点的入度所需时间为 O(e)，建立零入度顶点栈所需时间为 O(n)；在拓扑排序过程中，若有向图无环，每个顶进一次栈出一次栈，顶点入度减 1 的操作共执行了 e 次。所以总的时间复杂度为 O(n+e)。

当有向图中无环时，也可以利用深度优先搜索进行拓扑排序。因为图中无环，深度优先遍历不会死循环。进行深度优先遍历时，最先退出 DFS 函数的顶点即为出度为零的顶点，是拓扑有序序列的最后一个顶点。由此，按退出 DFS 函数的先后次序记录下来的顶点序列即为逆向的拓扑有序序列。

POJ 1094 Sorting It All Out @

An ascending sorted sequence of distinct values is one in which some form of a less-than operator is used to order the elements from smallest to largest. For example, the sorted sequence A, B, C, D implies that A < B, B < C and C < D. in this problem, we will give you a set of relations of the form A < B and ask you to determine whether a sorted order has been specified or not.

输入

    Input consists of multiple problem instances. Each
    instance starts with a line containing two positive
    integers n and m. the first value indicated the
    number of objects to sort, where 2 <= n <= 26.  The
    objects to be sorted will be the first n characters
    of the uppercase alphabet. The second value m
    indicates the number of relations of the form A < B
    which will be given in this problem instance. Next
    will be m lines, each containing one such relation
    consisting of three characters: an uppercase
    letter, the character "<" and a second uppercase
    letter. No letter will be outside the range of the
    first n letters of the alphabet.  Values of n = m = 0
    indicate end of input.

    4 6
    A<B
    A<C
    B<C
    C<D
    B<D
    A<B
    3 2
    A<B
    B<A
    26 1
    A<Z
    6 6
    A<F
    B<D
    C<E
    F<D
    D<E
    E<F
    0 0

输出

    For each problem instance, output consists of one
    line.  This line should be one of the following three:

    -   Sorted sequence determined after xxx relations: yyy...y.
    -   Sorted sequence cannot be determined.
    -   Inconsistency found after xxx relations.

    where xxx is the number of relations processed at
    the time either a sorted sequence is determined or
    an inconsistency is found, whichever comes first,
    and yyy...y is the sorted, ascending sequence.

    Sorted sequence determined after 4 relations: ABCD.
    Inconsistency found after 2 relations.
    Sorted sequence cannot be determined.
    Inconsistency found after 6 relations.

根据题目的要求，我们要每输入一次就要进行一次拓扑排序 topological_sort()，这样才能做到不成功（即发现有环）时，能知道是哪步不成功，并且给出输出。

还有要注意的就是如果我们可以提前判断结果了，但后面还有输入没完成，那么我们必须继续完成输入，不然剩下的输入会影响下一次 case 的输入。

// POJ 1094 Sorting It All Out, http://poj.org/problem?id=1094
#include <iostream>
#include <climits>
#include <stack>
#include <vector>

using namespace std;

const int MAX_NV  = 26;
const int GRAPH_INF = INT_MAX;

struct graph_t {
    int nv, ne;
    int matrix[MAX_NV][MAX_NV];
};

graph_t g;

int topological[MAX_NV];

int topo_sort( const graph_t *g, int topological[] ) {
    const int n = g->nv;
    vector<int> in_degree( n, 0 );
    for( int i = 0; i < n; ++i ) {
        for( int j = 0; j < n; ++j ) {
            if( g->matrix[i][j] < GRAPH_INF ) {
                ++in_degree[j];
            }
        }
    }

    stack<int> s;
    for( int i = 0; i < n; ++i ) {
        if( !in_degree[i] ) { s.push(i); }
    }

    int count = 0;
    bool insufficient = false;
    while( !s.empty() ) {
        if( s.size() > 1 ) { insufficient = true; }
        int u = s.top(); s.pop();                       // 删除顶点 u
        topological[count++] = u;
        --in_degree[u];                                 // 变成 -1，表示已经输出
        for( int i = 0; i < n; ++i ) {                  // 更新入度
            if( g->matrix[u][i] < GRAPH_INF ) {
                --in_degree[i];
            }
        }
        for( int i = 0; i < n; ++i ) {                  // 选择入度为 0 的顶点
            if( g->matrix[u][i] < GRAPH_INF ) {
                if( !in_degree[i] ) { s.push(i); }
            }
        }
    }

    if( count < n ) {
        return 0;
    } else {
        if( insufficient ) {                            // 有孤立点，说明条件不足
            return -1;
        } else {
            return 1;
        }
    }
}

int main() {
    int m;                                              // m 不一定是边的数目，因为输入边可能有重复

    while( 2 == scanf( "%d %d", &g.nv, &m ) && g.nv && m ) {
        bool finished = false;                          // 排序完成，结束，发现有环，可以提前结束
        for( int i = 0; i < g.nv; ++i ) {               // 初始化图，所有节点间距离为无穷大
            for( int j = 0; j < g.nv; ++j ) {
                g.matrix[i][j] = GRAPH_INF;
            }
        }
        for( int k = 0; k < m; ++k ) {                  // 读取边信息
            char s[5];
            scanf( "%s", s );
            g.matrix[s[0]-'A'][s[2]-'A'] = 1;
            if( finished ) { continue; }                // 完成，则 continue，消耗输入

            // 是否有环，0 表示有环
            const int ok = topo_sort( &g, topological );

            if( ok == 0 ) {                             // 有环存在
                printf( "Inconsistency found after %d relations.\n", k+1 );
                finished = true;                        // 提前结束，记住要继续消耗输入
            }
            if( ok == 1 && k ) {
                printf( "Sorted sequence determined after %d relations: ", k+1 );
                for( int i = 0; i < g.nv; ++i ) {
                    printf( "%c", 'A'+topological[i] );
                }
                printf( ".\n" );
                finished = true;
            }
            // ok == -1, continue
        }
        if( !finished ) {
            printf( "Sorted sequence cannot be determined.\n" );
        }
    }
    return 0;
}

关键路径 @

用有向边上的权值表示活动的持续时间，用顶点表示时间，这样的有向图叫做边表示的活动网络 (Activity On Edge Network)，简称 AOE 网络。

路径最长的路径叫做关键路径 (Critical Path)。假设开始点为 v₁，从 v₁ 到 v_i 的最长路径长度叫做事件 v_i 的最早发生时间。这个事件决定了所有以 v_i 为端点的弧所表示的活动的最早 (earliest) 开始时间。我们用 e(i) 表示活动 a_i 的最早开始时间。还可以定义一个活动的最迟 (latest) 开始时间 l(i)，这是在不推迟整个工程完成的前提下，活动 a_i 最迟必须开始进行的时间。两者之差 l(i)-e(i) 意味着完成活动 a_i 的时间余量。我们把 l(i) = e(i) 的活动叫做关键活动。

设活动 a_i 由弧 <j, k> 表示，为了求得活动的 e(i) 和 l(i)，首先应求得事件的最早发生时间 ve(j) 和最迟发生时间 vl(j)，其持续时间记为 dut(<j, k>)，则有如下关系

e(i) = ve(j)
l(i) = vl(k) - dut(<j, k>)

求 ve(j) 和 vl(k) 需分两步进行：

从 ve(0) = 0 开始向前递推

ve(j) = max{ ve(i)+dut(<i, j>) }, <i, j> ∈ T

其中 T 是所有以顶点 j 为弧头的边的集合。
从 vl(n-1) = ve(n-1) 起向后递推

vl(j) = min{ vl(k)-dut(<j, k>) }, <j, k> ∈ S

其中 S 是所有以顶点 j 为弧尾的边的集合。

有向图及其邻接矩阵

(a) 所示 AOE 网络的关键路径的计算过程}

Vertex      ve          vl         |    Activity    e           l           l-e
-----------------------------------+-------------------------------------------
v1          0           0          |    a1          0           1           1
v2          3     |     4     ^    |    a2          0           0           0
v3          2     |     2    /|\   |    a3          3           4           1
v4          6    \|/    6     |    |    a4          3           4           1
v5          6     V     7     |    |    a5          2           2           0
v6          8           8          |    a6          2           5           3
                                   |    a7          6           6           0
                                   |    a8          6           7           1

input:

    6 8
    A B 3
    A C 2
    C D 4
    B D 2
    C F 3
    B E 3
    E F 1
    D F 2

output:

    A C D F

邻接矩阵上的关键路径的 C 语言实现 @

#include <iostream>
#include <climits>
#include <stack>
#include <algorithm>

using namespace std;

const int MAX_NV = 100;
const int GRAPH_INF = INT_MAX;

struct graph_t {
    int nv, ne;
    int matrix[MAX_NV][MAX_NV];
};

graph_t g;

int topological[MAX_NV];
int path[MAX_NV];

// 按照拓扑排序的顺序，计算所有顶点的最早发生时间 ve.
// return:  无环返回 true，有环返回 false
bool toposort_ve( const graph_t &g, int topological[], int ve[] ) {
    const int n = g.nv;
    vector<int> in_degree( n, 0 );
    for( int i = 0; i < n; ++i ) {
        for( int j = 0; j < n; ++j ) {
            if( g.matrix[i][j] < GRAPH_INF ) {
                ++in_degree[j];
            }
        }
    }
    stack<int> s;
    for( int i = 0; i < n; ++i ) {
        if( !in_degree[i] ) { s.push(i); }
    }
    fill( ve, ve + n, 0 );

    int count = 0;
    while( !s.empty() ) {
        int u = s.top(); s.pop();
        topological[count++] = u;
        --in_degree[u];
        for( int i = 0; i < n; ++i ) {
            if( g.matrix[u][i] < GRAPH_INF ) {
                --in_degree[i];
            }
        }
        for( int i = 0; i < n; ++i ) {
            if( g.matrix[u][i] < GRAPH_INF && ve[i] < ve[u] + g.matrix[u][i] ) {
                ve[i] = ve[u] + g.matrix[u][i];
            }
        }
        for( int i = 0; i < n; ++i ) {
            if( g.matrix[u][i] < GRAPH_INF && !in_degree[i] ) {
                s.push(i);
            }
        }
    }

    if( count < n ) {
        return false;
    } else {
        return true;
    }
}

// 求关键路径，第一个顶点为起点，最后一个顶点为终点.
// ve:      所有事件的最早发生时间
// path:    关键路径
// return:  无环返回关键路径的顶点个数，有环返回 0
int critical_path( const graph_t &g, int path[MAX_NV] ) {
    int count = 0;
    vector<int> ve( g.nv );
    vector<int> vl( g.nv );

    if( !toposort_ve(g, topological, &ve[0]) ) {        // 有环
        return 0;
    }

    for( int i = 0; i < MAX_NV; ++i ) {
        path[i] = -1;
    }
    for( int i = 0; i < g.nv; ++i ) {
        vl[i] = ve[g.nv-1];                         // 初始化 vl 为最大
    }

    // 逆序计算 vl
    for( int i = g.nv-1; i >=0; i-- ) {
        int k = topological[i];
        for( int j = 0; j < g.nv; ++j ) {
            if( g.matrix[j][k] < GRAPH_INF && vl[j] > vl[k] - g.matrix[j][k] ) {
                vl[j] = vl[k] - g.matrix[j][k];
            }
        }
    }
    for( int i = 0; i < g.nv; ++i ) {
        for( int j = 0; j < g.nv; ++j ) {
            int e = ve[i];
            int l = vl[j] - g.matrix[i][j];
            if( e == l ) {
                if( i == 0 ) {
                    path[count++] = i;
                    path[count++] = j;
                } else {
                    path[count++] = j;
                }
            }
        }
    }

    return count;
}

int main() {
    scanf( "%d %d", &g.nv, &g.ne );
    for( int i = 0; i < g.nv; ++i ) {
        for( int j = 0; j < g.nv; ++j ) {
            g.matrix[i][j] = GRAPH_INF;
        }
    }
    for( int k = 0; k < g.ne; ++k ) {
        char chx[5], chy[5];
        int w;
        scanf( "%s %s %d", chx, chy, &w );
        g.matrix[*chx-'A'][*chy-'A'] = w;
    }

    int count = critical_path( g, path );
    for( int i = 0; i < count; ++i ) {
        printf( "%c ", 'A'+path[i] );
    }
    printf( "\n" );
    return 0;
}

一次正向，复杂度为 O(n²)，一次逆向，复杂度为 O(n²)，因此，该算法的复杂度为 O(n²)。

组合类深度优先搜索 Combination Related DFS
排列类深度优先搜索 Permutation Related DFS

【下面是强化班内容】

✂️ 2016/08/21 上午 7:00:00 FLAG 算法面试难度提高？如何准备？【免费试听】 @

HR 面试这一环可能会问到的问题 @
What are your strengths?
- I’m passionate about programming and I can write high quality code. Besides, I have solid mathematical foundation and know a little about machine learning.
- I’m a quick learner and I love programming. Because I love it, I’m willing to spend my time, money, and energy into it.
What is your greatest weakness?

I live in campus for a little long time, so I haven’t write as much code as people at my age. Compared to people who started to work immediately after graduation, I have less real experience in production environment.

Why should I hire you?

My technical skills match Facebook

Five year plan?

I aims to become a world class topnotch developer in (Programming Lagnuage Design, Distributed system, Machine Learning, Data Mining etc).

I want to solve hardcore technical problems with smart guys.

I want to have a small and smart team, to build some world class tools. I tend to be more satisfied and happy when people can fully appreciate my work, so instead of user products, personally I prefer developer oriented tools/platforms, such as storage systems like HBase and Hive, or significant improvement of existing language implementations (for example, Facebook’s HipHop for PHP, Google’s V8 for JavaScript, Delvik for Java on mobile platform).

why Google?

In my opinion, Google is the most innovative company on the Earth. It created many successful products, for example web search engine, Android, Gmail. But it doesn’t stop, it creates many products that sounds incredible, like Google driveless car, Google Glass etc.

That’s why I want to join Google and take part in making fantastic products.

why Facebook?

First, Facebook is a cool company, which has strong geek culture. The CEO, Mark Zuckerberg is a geek, and he recognises the value of engineers, today Facebook is still dominated by engineers, not product managers. Second, Facebook is the world’s biggest social network website, in there my code will serve billions of people, which makes me feel a big sense of achievement.

Any questions?

Facebook

There is a saying often said: Facebook and Google gathered a bunch of smartest people in the world, but they are just thinking day and night to attempt people to click all their ads! This sounds sad but it’s somewhat true. I don’t like ads, and I’m a big fan of adblock. How do you and Facebook engineers think about this saying?

Is there any projects related to language design and implementation other than HipHop in Facebook? I heard that Facebook is actively developing a new PHP virtual machine, can I have some detail information?

Is Facebook chat still powered by Erlang? What’s the most challenging part of Facebook chat? How do you deal with spamming?

Amazon

Google has developed Spanner and F1, is Amazon developing its own large scale RDBMS? If not, why?

When I worked in Baidu, all SDE must keep their mobile phone online 7x24, and be ready to be called at any time in case of online accidents. What’s the process in Amazon to handle emergent online accidents? What’s the division of labour?

AeroFS

Would please tell me something about your tool chain?

Take LinkedIn as an example, free users’ data are exactly the thing that commercial users want. Although AeroFS is quite different, do you have any idea to make your commercial users benifit from your free users?

Dropbox turned to online music area, how do you think about this? Is this a signal that indicating personal cloud storage is not profitable enough?

refs and see also
- Top 10 HR Interview Questions & How To Answer Them | Human Resources Blog | Top HR Blog
- HR 面试这一环可能会问到的问题 · soulmachine/acm-cheat-sheet Wiki · GitHub
各类 IT 企业的面试算法难度及风格
如何解决中等难度以上的算法题
如何解决 follow up 问题

Two sum @

排序再夹逼。但是返回的是 index！

class Solution {
public:
    vector<int> twoSum(vector<int> &nums, int target) {
        unordered_map<int, int> mapping;
        vector<int> result;
        for (int i = 0; i < nums.size(); i++) {
            mapping[nums[i]] = i;                                                   // 对应到 index
        }
        for (int i = 0; i < nums.size(); i++) {
            const int gap = target - nums[i];
            if (mapping.find(gap) != mapping.end() && mapping[gap] > i) {           // 对每个元素尝试找到匹配
                result.push_back(i + 1);
                result.push_back(mapping[gap] + 1);
                break;
            }
        }
        return result;
    }
};

或者用一种巧妙地夹逼：

class Solution {
public:
    vector<int> twoSum(vector<int> &a, int s) {
        vector<int> r(a.size());
        iota(r.begin(), r.end(), 0);
        // 存储 index，然后把  index 排序。结果是 a[r[i]] 升序排列（for i = [0,n)）。
        sort(r.begin(), r.end(), [&](int x, int y) { return a[x] < a[y]; });
        for (size_t i = 0, j = a.size()-1; i < j; i++) {        // i 在左，j 在右，i 用 for 循环
            while (j > i+1 && a[r[i]]+a[r[j]] > s) j--;         // j 不断下调
            if (a[r[i]]+a[r[j]] == s) {
                int x = r[i], y = r[j];
                r.clear();  // 还用 r 来存输出结果……
                if (x > y) swap(x, y);
                r.push_back(x);
                r.push_back(y);
                break;
            }
        }
        return r;
    }
};

class Solution {
public:
    vector<int> twoSum(vector<int> &nums, int target) {
        unordered_map<int, int> mapping;
        for (int i = 0; i < nums.size(); i++) {
            mapping[nums[i]] = i;
        }
        sort( nums.begin(), nums.end() );
        int lo = 0, hi = nums.size()-1;
        while( lo < hi ) {
            if( nums[lo]+nums[hi] == target ) {
                break;
            } else if( nums[lo]+nums[hi] < target) {
                ++lo;
            } else {
                --hi;
            }
        }

        vector<int> result;
        if( lo < hi ) {
            int x = mapping[nums[lo]];
            int y = mapping[nums[hi]];
            if( x > y ) { swap(x,y); }
            result.push_back( x );
            result.push_back( y );
        }
        return result;
    }
};

我的这个版本居然错在了……一个蛋疼的例子：

Input:      [0,4,3,0]
            0
Output:     [3,3]
Expected:   [0,3]

Two sum follow up I @

: 如果 array 是排序好的呢？

[Two Sum II - Input array is sorted | LeetCode OJ](https://leetcode.com/problems/two-sum-ii-input-array-is-sorted/) `@`{.fold}

:   题设保证了有唯一解。

    ```
    class Solution {
    public:
        vector<int> twoSum(vector<int> &a, int target) {
            int i = 0, j = a.size()-1;
            while (i < j) {
                if (a[i]+a[j] < target)
                    i++;
                else if (a[i]+a[j] > target)
                    j--;
                else
                    break;
            }
            return {i+1, j+1};
        }
    };
    ```

    吐槽：two sum 的题，把 index 改成了 zero-based，而这里，居然还是 one-based。

[3Sum | LeetCode OJ](https://leetcode.com/problems/3sum/) `@`{.fold}

:   可能有多组解。三个数合为 0。

    ```cpp
    class Solution {
    public:
        vector<vector<int> > threeSum(vector<int> &a) {
            int n = a.size();
            vector<vector<int>> r;
            sort(a.begin(), a.end());
            for (int i = 0; i < n; ) {
                int j = i+1, k = n-1, s = -a[i], old;   // 对每个 i，夹逼尝试 j、k。
                while (j < k) {
                    if (a[j]+a[k] < s) j++;
                    else if (a[j]+a[k] > s) k--;
                    else {
                        r.push_back(vector<int>{a[i], a[j], a[k]});
                        old = a[j];
                        while (++j < k && a[j] == old);
                        k--;
                    }
                }
                old = a[i];
                while (++i < n && a[i] == old);
            }
            return r;
        }
    };
    ```

[3Sum Closest | LeetCode OJ](https://leetcode.com/problems/3sum-closest/) `@`{.fold}

:   和刚才的情况类似。

    ```cpp
    #define REP(i, n) for (int i = 0; i < (n); i++)

    class Solution {
    public:
        int threeSumClosest(vector<int> &a, int target) {
            int n = a.size(), opt = INT_MAX, opts;
            sort(a.begin(), a.end());
            REP(i, n) {
                int j = i+1, k = n-1, t = target-a[i];
                while (j < k) {
                    if (a[j]+a[k] < t) {
                        if (t-a[j]-a[k] < opt) {
                            opt = t-a[j]-a[k];
                            opts = a[i]+a[j]+a[k];
                        }
                        j++;
                    } else if (a[j]+a[k] > t) {
                        if (a[j]+a[k]-t < opt) {
                            opt = a[j]+a[k]-t;
                            opts = a[i]+a[j]+a[k];
                        }
                        k--;
                    } else
                        return target;
                }
            }
            return opts;
        }
    };
    ```

[4Sum | LeetCode OJ](https://leetcode.com/problems/4sum/) `@`{.fold}

:   ```cpp
    class Solution {
    public:
        vector<vector<int> > fourSum(vector<int> &a, int target) {
            int n = a.size(), old;
            multimap<int, int> m;
            vector<vector<int>> r;
            sort(a.begin(), a.end());
            for (int i = 0; i < n; ) {
                // a <= b < c <= d
                for (int j = i+1; j < n; ) {
                    int t = target-a[i]-a[j];
                    auto it = m.equal_range(t);
                    for (; it.first != it.second; ++it.first) {
                        vector<int> b{it.first->second, t-it.first->second, a[i], a[j]};
                        r.push_back(b);
                    }
                    old = a[j];
                    while (++j < n && a[j] == old);
                }
                // a < b = b <= c
                if (i+1 < n && a[i] == a[i+1]) {
                    for (int j = i+2; j < n; ) {
                        int t = target-a[i]*2-a[j];
                        auto it = lower_bound(a.begin(), a.begin()+i, t);
                        if (it != a.begin()+i && *it == t) {
                            vector<int> b{*it, a[i], a[i], a[j]};
                            r.push_back(b);
                        }
                        old = a[j];
                        while (++j < n && a[j] == old);
                    }
                }
                // a = a = a <= b
                if (i+2 < n && a[i] == a[i+2]) {
                    int t = target-a[i]*3;
                    auto it = lower_bound(a.begin()+i+3, a.end(), t);
                    if (it != a.end() && *it == t) {
                        vector<int> b{a[i], a[i], a[i], t};
                        r.push_back(b);
                    }
                }
                old = a[i];
                while (i+1 < n && a[i+1] == old)
                    i++;
                for (int j = 0; j < i; ) {
                    m.insert(make_pair(a[j]+a[i], a[j]));
                    old = a[j];
                    while (++j < n && a[j] == old);
                }
                i++;
            }
            return r;
        }
    };
    ```

1. Two sum follow up II - Triangle count @

Kth largest element
- 1. 第 k 大元素的三层递进面试考察.
- 1. 如何通过一道题区分 3 类面试者
- 1. 剖析面试官面试的思路

✂️ 2016/08/28 上午 7:00:00 数据结构 Data Structure (上) @

并查集 @

basics ideas @

并查集的基本原理
并查集的相关运用
并查集的拓展（带路径压缩）
并查集的运用

并查集又称不相交集，有两个名字的原因在于它原就有两个不同的英文名字，Disjoint sets和Union-find set。更准确点应该说并查集是用来操作不相交集的数据结构。算法导论上这一章就叫用于不相交集合的数据结构（Data Structures for Disjoint Sets）。维基百科上也说：

In computer science, a disjoint-set data structure, also called a union–find data structure or merge–find set, is a data structure that keeps track of a set of elements partitioned into a number of disjoint (nonoverlapping) subsets. It supports two useful operations:

Find: Determine which subset a particular element is in. Find typically returns an item from this set that serves as its “representative”; by comparing the result of two Find operations, one can determine whether two elements are in the same subset.
Union: Join two subsets into a single subset.

但一般说 Disjoint Sets 就指的是Data Structures for Disjoint Sets。

Disjoint-set data structure @

Disjoint-set forests

In a disjoint-set forest, the representative of each set is the root of that set’s tree. Find follows parent nodes until it reaches the root. Union combines two trees into one by attaching the root of one to the root of the other. One way of implementing these might be:

function MakeSet(x)
    x.parent := x

function Find(x)
    if x.parent == x
       return x
    else
       return Find(x.parent)

function Union(x, y)
    xRoot := Find(x)
    yRoot := Find(y)
    xRoot.parent := yRoot

the tree it creates can be highly unbalanced -> two ways to solve.

function MakeSet(x)
    x.parent := x
    x.rank   := 0

function Union(x, y)
    xRoot := Find(x)
    yRoot := Find(y)
    if xRoot == yRoot
        return

    // x and y are not already in same set. Merge them.
    if xRoot.rank < yRoot.rank
        xRoot.parent := yRoot
    else if xRoot.rank > yRoot.rank
        yRoot.parent := xRoot
    else
        yRoot.parent := xRoot
        xRoot.rank := xRoot.rank + 1

function Find(x)
    if x.parent != x
       x.parent := Find(x.parent)
    return x.parent

Union-Find Sets, c code @

ufs.c @

#include <stdlib.h>

typedef struct ufs_t {
    int *p;                         // 树的双亲表示法
    int size;
} ufs_t;

ufs_t* ufs_create( int n ) {
    ufs_t *ufs = (ufs_t *)malloc(sizeof(ufs_t));
    ufs->p = (int*)malloc(n * sizeof(int));
    for( int i = 0; i < n; ++i ) {
        ufs->p[i] = -1;             // init to disjoint, every node is root
    }
    return ufs;
}

void ufs_destroy( ufs_t *ufs ) {
    free( ufs->p );
    free( ufs );
}

// 带路径压缩，递归版, return index
int ufs_find( ufs_t *ufs, int x ) {
    if( ufs->p[x] < 0 ) { return x; }
    return ufs->p[x] = ufs_find( ufs, ufs->p[x] );      // parent
}

// 朴素版, deprecated
static int ufs_find_naive( ufs_t *ufs, int x ) {
    while( ufs->p[x] >= 0 ) {
        x = ufs->p[x];
    }
    return x;
}

// 带路径压缩，迭代版
static int ufs_find_iterative( ufs_t *ufs, int x ) {
    int oldx = x;
    while( ufs->p[x] >= 0 ) {
        x = ufs->p[x];              // log the parent
    }
    while( oldx != x ) {
        int temp = ufs->p[oldx];    // go up, up and up. assign the x.
        ufs->p[oldx] = x;
        oldx = temp;
    }
    return x;
}

int ufs_union( ufs_t *ufs, int x, int y ) {
    const int rx = ufs_find(ufs, x);
    const int ry = ufs_find(ufs, y);
    if( rx == ry ) { return -1; }

    ufs->p[rx] += ufs->p[ry];
    ufs->p[ry] = rx;
    return 0;
}

int ufs_set_size( ufs_t *ufs, int x ) {
    const int rx = ufs_find(ufs, x);
    return -ufs->p[rx];
}

infected student @

#include <stdio.h>

#define MAXN 30000

#include "ufs.c"

int main() {
    int n, m, k;
    while( scanf("%d%d", &n, &m) && n > 0 ) {
        ufs_t *ufs = ufs_create(MAXN);
        while( m-- ) {
            int x, y;                           // two students
            int rx, ry;                         // x, y 所属的集合的根
            scanf("%d", &k);

            scanf("%d", &x); k--;
            rx = ufs_find(ufs, x);
            while( k-- ) {
                scanf("%d", &y);
                ry = ufs_find( ufs, y );
                ufs_union( ufs, rx, ry );       // merge y to x
            }
        }
        printf( "%d\n", ufs_set_size(ufs, 0) );
        ufs_destroy(ufs);
    }
    return 0;
}

$ cat input.txt
100 4
2 1 2
5 10 13 11 12 14
2 0 1
2 99 2

200 2
1 5
5 1 2 3 4 5

1 0
0 0

$ cat input.txt | ./a.out
4
1
1

C++ Version:

#include <vector>
#include <cstdio>

using namespace std;

struct UFS {
    explicit UFS( int n ) {
        arr = vector<int>(n, -1);
    }
    int _find( int idx ) {
        int oldidx = idx;
        while( arr[idx] >= 0 ) { idx = arr[idx]; }
        while( oldidx != idx ) {
            int next = arr[oldidx];
            arr[oldidx] = idx;
            oldidx = next;
        }
        return idx;
    }
    void _union( int a, int b ) {
        int ra = _find(a);
        int rb = _find(b);
        if( ra == rb ) { return; }  // !!!
        arr[ra] += arr[rb];
        arr[rb] = ra;
    }
    int _size( int a ) {
        return -arr[_find(a)];
    }
    vector<int> arr;
};

int main() {
    int n, m, k;
    while( scanf("%d%d", &n, &m) && n > 0 ) {
        UFS ufs(n);
        while( m-- ) {
            int x, y;                           // two students
            int rx, ry;                         // x, y 所属的集合的根
            scanf("%d", &k);

            scanf("%d", &x); k--;
            rx = ufs._find(x);
            while( k-- ) {
                scanf("%d", &y);
                ufs._union( rx, y );
            }
        }
        printf( "%d\n", ufs._size(0) );
    }
    return 0;
}

食物链 @

动物王国中有三类动物 A,B,C，这三类动物的食物链构成了有趣的环形。A 吃 B， B 吃 C，C 吃 A。现有 N 个动物，从 1 到 N 编号。每个动物都是 A,B,C 中的一种，但是我们并不知道它到底是哪一种。

有人用两种说法对这 N 个动物所构成的食物链关系进行描述：

第一种说法是“1 X Y”，表示X和Y是同类。
第二种说法是“2 X Y”，表示X吃Y。

此人对 N 个动物，用上述两种说法，一句接一句地说出 K 句话，这 K 句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

当前的话与前面的某些真的话冲突，就是假话；
当前的话中 X 或 Y 比 N 大，就是假话；
当前的话表示 X 吃 X，就是假话。

你的任务是根据给定的 N(1 < N < 50,000) 和 K 句话 (0 <= K <=100,000 )，输出假话的总数。

输出只有一个整数，表示假话的数目。

input:

    第一行是两个整数 N 和 K，以一个空格分隔。

    以下 K 行每行是三个正整数 D，X，Y，两数之间用一个空格隔开，其中 D 表示说法的种类。

    -   若 D=1，则表示 X 和 Y 是同类。
    -   若 D=2，则表示 X 吃 Y。

    100 7
    1 101 1
    2 1 2
    2 2 3
    2 3 3
    1 1 3
    2 3 1
    1 5 5

output:

    3

/* POJ 1182 食物链, Catch them, http://poj.org/problem?id=1182 */
#include <stdio.h>
#include <stdlib.h>

typedef struct ufs_t {
    int *p;
    int *dist;                          // 表示 x 与父节点 p[x] 的关系，0 表示 x 与 p[x] 是同类，1 表示 x 吃 p[x]，2 表示 p[x] 吃 x
    int size;
} ufs_t;

ufs_t* ufs_create(int n) {
    ufs_t *ufs = (ufs_t*)malloc(sizeof(ufs_t));
    ufs->p = (int*)malloc(n * sizeof(int));
    ufs->dist = (int*)malloc(n * sizeof(int));
    for( int i = 0; i < n; ++i ) {
        ufs->p[i] = -1;
        ufs->dist[i] = 0;               // 自己与自己是同类
    }
    return ufs;
}

void ufs_destroy( ufs_t *ufs ) {
    free( ufs->p );
    free( ufs->dist );
    free( ufs );
}

int ufs_find( ufs_t *ufs, int x ) {
    if( ufs->p[x] < 0 ) { return x; }

    const int parent = ufs->p[x];
    ufs->p[x] = ufs_find( ufs, ufs->p[x] );
    ufs->dist[x] = (ufs->dist[x] + ufs->dist[parent]) % 3;  // ???
    return ufs->p[x];
}

int ufs_union( ufs_t *ufs, int root1, int root2 ) {
    if( root1 == root2 ) { return -1; }
    ufs->p[root1] += ufs->p[root2];
    ufs->p[root2] = root1;
    return 0;
}

void ufs_add_relation( ufs_t *ufs, int x, int y, int relation ) {
    const int rx = ufs_find(ufs, x);
    const int ry = ufs_find(ufs, y);
    ufs_union( ufs, ry, rx );                               // 注意顺序！
    // rx 与 x 关系 + x 与 y 的关系 + y 与 ry 的关系 = rx 与 ry 的关系
    ufs->dist[rx] = (ufs->dist[y] - ufs->dist[x] + 3 + relation) % 3;
}

int main() {
    int result = 0;                                         // 假话的数目

    ufs_t *ufs;
    int n, k;
    scanf("%d%d", &n, &k);
    ufs = ufs_create(n + 1);

    while( k-- ) {
        int d, x, y;
        scanf("%d%d%d", &d, &x, &y);

        if (x > n || y > n || (d == 2 && x == y)) {
            result++;
        } else {
            const int rx = ufs_find(ufs, x);
            const int ry = ufs_find(ufs, y);

            if (rx == ry) {                                 // 若在同一个集合则可确定x和y的关系
                if((ufs->dist[x] - ufs->dist[y] + 3) % 3 != d - 1)
                    result++;
            } else {
                ufs_add_relation(ufs, x, y, d-1);
            }
        }
    }

    printf("%d\n", result);
    ufs_destroy( ufs );
    return 0;
}

refs and see also

Trie 树 @

Trie 理论知识 @
In computer science, a trie(/ˈtraɪ/, as “try”), also called digital tree and sometimes radix tree or prefix tree (as they can be searched by prefixes), is a kind of search tree—an ordered tree data structure that is used to store a dynamic set or associative array where the keys are usually strings. Unlike a binary search tree, no node in the tree stores the key associated with that node; instead, its position in the tree defines the key with which it is associated. All the descendants of a node have a common prefix of the string associated with that node, and the root is associated with the empty string. Values are not necessarily associated with every node. Rather, values tend only to be associated with leaves, and with some inner nodes that correspond to keys of interest. For the space-optimized presentation of prefix tree, see compact prefix tree.

A trie for keys “A”,“to”, “tea”, “ted”, “ten”, “i”, “in”, and “inn”.

a trie has a number of advantages over binary search trees. A trie can also be used to replace a hash table, over which it has the following advantages:
- Looking up data in a trie is faster in the worst case, O(m) time (where m is the length of a search string), compared to an imperfect hash table. An imperfect hash table can have key collisions. A key collision is the hash function mapping of different keys to the same position in a hash table. The worst-case lookup speed in an imperfect hash table is O(N) time, but far more typically is O(1), with O(m) time spent evaluating the hash.
- There are no collisions of different keys in a trie.
- Buckets in a trie, which are analogous to hash table buckets that store key collisions, are necessary only if a single key is associated with more than one value.
- There is no need to provide a hash function or to change hash functions as more keys are added to a trie.
- A trie can provide an alphabetical ordering of the entries by key.
Tries do have some drawbacks as well:
- Tries can be slower in some cases than hash tables for looking up data, especially if the data is directly accessed on a hard disk drive or some other secondary storage device where the random-access time is high compared to main memory.
- Some keys, such as floating point numbers, can lead to long chains and prefixes that are not particularly meaningful. Nevertheless, a bitwise trie can handle standard IEEE single and double format floating point numbers.
- Some tries can require more space than a hash table, as memory may be allocated for each character in the search string, rather than a single chunk of memory for the whole entry, as in most hash tables.
Suffix tree @

In computer science, a suffix tree (also called PAT tree or, in an earlier form, position tree) is a compressed trie containing all the suffixes of the given text as their keys and positions in the text as their values. Suffix trees allow particularly fast implementations of many important string operations.

doubly chained tree @
A trie implemented as a doubly chained tree: vertical arrows are child pointers, dashed horizontal arrows are next pointers. The set of strings stored in this trie is {baby, bad, bank, box, dad, dance}. The lists are sorted to allow traversal in lexicographic order.

Every multi-way or k-ary tree structure studied in computer science admits a representation as a binary tree, which goes by various names including 【child-sibling representation】, 【left-child, right-sibling binary tree】, 【doubly chained tree】 or 【filial-heir chain】(['fɪlɪəl]).

6-ary tree represented as a binary tree

The process of converting from a k-ary tree to an LC-RS binary tree is sometimes called the 【Knuth transform】.

1 1 1 /|\ / / / | \ / 2 / | \ / / \ 2 3 4 2---3---4 5 3 / \ | / / \ \ 5 6 7 5---6 7 6 4 / \ / / 8 9 8---9 7 / 8 \ 9
refs and see also
Trie 树的相关运用

Trie tree @

trie_tree.c @

#include <stdio.h>
#include <string.h>
#include <stdlib.h>

#define MAXN 10000
#define CHAR_COUNT  10                      // 字符的种类，也即单个节点的子树的最大个数
#define MAX_CODE_LEN 10
#define MAX_NODE_COUNT  (MAXN * MAX_CODE_LEN + 1)  /** 字典树的最大节点个数. */
                   /* 如果没有指定 MAXN，则是 CHAR_COUNT^(MAX_CODE_LEN+1)-1 */

typedef struct trie_node_t {
    struct trie_node_t* next[CHAR_COUNT];
    bool is_tail;                           // 当前字符是否位于某个串的尾部
} trie_node_t;

typedef struct trie_tree_t {
    trie_node_t *root;                      /** 树的根节点 */
    int size;
    trie_node_t nodes[MAX_NODE_COUNT];
} trie_tree_t;

trie_tree_t* trie_tree_create(void) {
    trie_tree_t *tree = (trie_tree_t*)malloc(sizeof(trie_tree_t));
    tree->root = tree->nodes;
    memset(tree->nodes, 0, sizeof(tree->nodes));
    tree->size = 1;
    return tree;
}

void trie_tree_destroy(trie_tree_t *tree) {
    free(tree);
    tree = NULL;                            // not necessary
}

void trie_tree_clear(trie_tree_t *tree) {
    memset(tree->nodes, 0, sizeof(tree->nodes));
    tree->size = 1;                         // 清空时一定要注意这一步！
}

bool trie_tree_insert(trie_tree_t *tree, char *word) {
    int i;
    trie_node_t *p = tree->root;
    while (*word) {
        int curword = *word - '0';
        if (p->next[curword] == NULL) {
            p->next[curword] = &(tree->nodes[tree->size++]);
        }
        p = p->next[curword];
        if (p->is_tail) {
            return false;                   // 某串是当前串的前缀
        }
        ++word;
    }

    p->is_tail = true;                      // 标记当前串已是结尾

    // 判断当前串是否是某个串的前缀
    for (i = 0; i < CHAR_COUNT; i++) {
        if (p->next[i] != NULL) {
            return false;
        }
    }
    return true;
}

immediate decodebility @

POJ 1056 IMMEDIATE DECODABILITY, http://poj.org/problem?id=1056

An encoding of a set of symbols is said to be immediately decodable if no code for one symbol is the prefix of a code for another symbol. We will assume for this problem that all codes are in binary, that no two codes within a set of codes are the same, that each code has at least one bit and no more than ten bits, and that each set has at least two codes and no more than eight.

Examples: Assume an alphabet that has symbols {A, B, C, D}.

The following code is immediately decodable:

A:01 B:10 C:0010 D:0000

but this one is not:

A:01 B:10 C:010 D:0000 (Note that A is a prefix of C)

输入

Write a program that accepts as input a series of groups of records from standard input. Each record in a group contains a collection of zeroes and ones representing a binary code for a different symbol. Each group is followed by a single separator record containing a single 9; the separator records are not part of the group. Each group is independent of other groups; the codes in one group are not related to codes in any other group (that is, each group is to be processed independently).

输出

For each group, your program should determine whether the codes in that group are immediately decodable, and should print a single output line giving the group number and stating whether the group is, or is not, immediately decodable.

#include "trie_tree.c"

int main() {
    int T = 0;
    char line[MAX_NODE_COUNT];
    trie_tree_t *trie_tree = trie_tree_create();
    bool islegal = true;

    while ( scanf("%s", line) != EOF ) {
        if (strcmp(line, "9") == 0) {
            if (islegal) {
                printf("Set %d is immediately decodable\n", ++T);
            } else {
                printf("Set %d is not immediately decodable\n", ++T);
            }
            trie_tree_clear(trie_tree);
            islegal = true;
        } else {
            if (islegal) {
                islegal = trie_tree_insert(trie_tree, line);
            }
        }
    }
    trie_tree_destroy(trie_tree);
    return 0;
}

$ cat input.txt | ./a.out
Set 1 is immediately decodable
Set 2 is not immediately decodable

compiled, and okay.

C++ version:

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <string>
#include <vector>
#include <iostream>
#include <algorithm>

using namespace std;

struct TrieTree {

    explicit TrieTree() { clear(); }

    const static int CHARCOUNT = 10;
    const static int NODECOUNT = 10*100;
    struct TrieTreeNode {
        bool isTail;
        TrieTreeNode *next[CHARCOUNT];
        TrieTreeNode() : isTail(false) { fill( next, next+CHARCOUNT, (TrieTreeNode *)0 ); }
    } *root;
    int size;
    vector<TrieTreeNode> nodes;

    void clear() {
        size  = 1;
        nodes = vector<TrieTreeNode>( NODECOUNT, TrieTreeNode() );
        root  = &nodes[0];
    }

    bool insert( const string &word ) {
        int n = word.size();
        TrieTreeNode *p = root;
        for( int i = 0; i < n; ++i ) {
            int idx = word[i] - '0';
            if( !p->next[idx] ) {
                p->next[idx] = &nodes[size++];
            }
            p = p->next[idx];
            if( p->isTail ) { return false; }
        }
        p->isTail = true;
        for( int i = 0; i< CHARCOUNT; ++i ) {
            if( p->next[i] ) {
                return false;
            }
        }
        return true;
    }
};

int main() {

    bool islegal = true;
    TrieTree tt;
    string line;
    int T = 0;

    while( getline( cin, line ) ) {
        if( line == "9" ) {
            printf( "Set %d is %simmediately decodable\n", ++T, islegal ? "" : "not " );
            tt.clear();
            islegal = true;
        } else {
            if (islegal) { islegal = tt.insert( line ); }
        }
    }
    return 0;
}

TODO: Node *next[CHARCOUNT] -> int next[CHARCOUNT], see Hardwood Species for HOWTO.

Hardwood Species @

input @

Red Alder
Ash
Aspen
Basswood
Ash
Beech
Yellow Birch
Ash
Cherry
Cottonwood
Ash
Cypress
Red Elm
Gum
Hackberry
White Oak
Hickory
Pecan
Hard Maple
White Oak
Soft Maple
Red Oak
Red Oak
White Oak
Poplan
Sassafras
Sycamore
Black Walnut
Will

output @

Ash 13.7931
Aspen 3.4483
Basswood 3.4483
Beech 3.4483
Black Walnut 3.4483
Cherry 3.4483
Cottonwood 3.4483
Cypress 3.4483
Gum 3.4483
Hackberry 3.4483
Hard Maple 3.4483
Hickory 3.4483
Pecan 3.4483
Poplan 3.4483
Red Alder 3.4483
Red Elm 3.4483
Red Oak 6.8966
Sassafras 3.4483
Soft Maple 3.4483
Sycamore 3.4483
White Oak 10.3448
Willow 3.4483
Yellow Birch 3.4483

code.cpp @

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <string>
#include <vector>
#include <iostream>
#include <algorithm>

using namespace std;

struct TrieTree {

    explicit TrieTree() { clear(); }

    const static int CHARCOUNT = 128;                           // ascii code
    const static int NODECOUNT = 128*100;
    struct TrieTreeNode {
        int next[CHARCOUNT];                                    // actually we can save count into next[0]
        int count;
        TrieTreeNode() : count(0) { fill( next, next+CHARCOUNT, 0 ); }
    };

    void insert( const string &word ) {
        int n = word.size();
        int p = 0;
        for( int i = 0; i < n; ++i ) {
            int idx = word[i];
            if( !nodes[p].next[idx] ) {
                nodes[p].next[idx] = nodes.size();
                nodes.push_back( TrieTreeNode() );
            }
            p = nodes[p].next[idx];
        }
        ++nodes[p].count;
    }

    void dfs( int r, const int n ) {
        if( nodes[r].count ) {
            word[pos] = '\0';
            printf( "%s %0.4f\n", word, ((float)nodes[r].count * 100) / n );
        }
        for( int i = 0; i < CHARCOUNT; ++i ) {
            if( nodes[r].next[i] ) {
                word[pos] = i;
                ++pos;
                dfs( nodes[r].next[i], n );
                --pos;
            }
        }
    }

    void clear() {
        nodes = vector<TrieTreeNode>( 1, TrieTreeNode() );
    }
    void reset() { pos = 0; }

    vector<TrieTreeNode> nodes;
    char word[50];
    int pos;
};

int main() {

    TrieTree tt;
    string line;

    int n = 0;
    while( getline( cin, line ) ) {
        tt.insert( line );
        ++n;
    }
    tt.reset();
    tt.dfs( 0, n );
    return 0;
}

扫描线算法

1. 扫描线的常规题目
1. 扫描线和其他数据结构结合的拓展

Interval Tree @

balanced line up @

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <limits.h>

#define MAXN 50001                          // 0 位置未用
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
#define L(a) ((a)<<1)
#define R(a) (((a)<<1)+1)

typedef struct node_t {
    int left, right;
    int max, min;
} node_t;

int A[MAXN];

// 完全二叉树，结点编号从 1 开始，层次从 1 开始.
// 用一维数组存储完全二叉树，空间约为 4N，
// 参考 http://comzyh.tk/blog/archives/479/
node_t node[MAXN * 4];

int minx, maxx;                             // 存放查询的结果

void init() { memset(node, 0, sizeof(node)); }

// 以 t 为根结点，为区间 A[l,r] 建立线段树
void build(int t, int l, int r) {
    node[t].left = l, node[t].right = r;
    if (l == r) {
        node[t].max = node[t].min = A[l];
        return;
    }
    const int mid = (l + r) / 2;
    build(L(t), l, mid);
    build(R(t), mid + 1, r);
    node[t].max = max( node[L(t)].max, node[R(t)].max );
    node[t].min = min( node[L(t)].min, node[R(t)].min );
}

// 查询根结点为 t，区间为 A[l,r] 的最大值和最小值
void query(int t, int l, int r) {
    if (node[t].left == l && node[t].right == r) {
        if (maxx < node[t].max)
            maxx = node[t].max;
        if (minx > node[t].min)
            minx = node[t].min;
        return;
    }
    const int mid = (node[t].left + node[t].right) / 2;
    if (l > mid) {
        query(R(t), l, r);
    } else if (r <= mid) {
        query(L(t), l, r);
    } else {
        query(L(t), l, mid);
        query(R(t), mid + 1, r);
    }
}

int main() {
    int n, q, i;

    scanf("%d%d", &n, &q);
    for (i = 1; i <= n; i++) scanf("%d", &A[i]);

    init();
    // 建立以 tree 为根结点，区间为 A[1,n] 的线段树
    build(1, 1, n);

    while (q--) {
        int a, b;
        scanf("%d%d", &a, &b);
        maxx = 0;
        minx = INT_MAX;
        query(1, a, b);                 // 查询区间 A[a,b] 的最大值和最小值
        printf("%d\n", maxx - minx);
    }
    return 0;
}

input:

C++ Version:

#include <cstdio>
#include <vector>

using namespace std;

struct IntervalTree {
    struct Node {
        int left, right, max, min;
        Node( int l = 0, int r = 0, int ma = 0, int mi = 0 ) : left(l), right(r), max(ma), min(mi) {}
    };
    explicit IntervalTree( int n ) : n(n) {
        arr     =   vector<int>( n+1 );
        node    =   vector<Node>( 4*(n+1), Node() );
    }
    void build( int root, int left, int right ) {
        Node &r = node[root];
        r.left  = left;
        r.right = right;
        if( left == right ) {
            r.max = r.min = arr[left];
            return;
        }
        int mid = (left+right)/2;
        build( 2*root,      left,       mid     );
        build( 2*root+1,    mid+1,      right   );
        r.max = max( node[2*root].max, node[2*root+1].max );
        r.min = min( node[2*root].min, node[2*root+1].min );
    }
    void print() {
        printf( "A: [ " );
        for( int i = 1; i <= n; ++i ) {
            printf( "%d ", arr[i] );
        }
        printf( "].\n" );
        for( int i = 1; i <= 4*n; ++i ) {
            Node &n = node[i];
            if( !n.left || !n.right ) { continue; }
            printf( "%d: [l: %d, r: %d, min: %d, max: %d]\n", i, n.left, n.right, n.min, n.max );
        }
    }

    void query( int root, int left, int right, int &maxx, int &minx ) {
        Node &r = node[root];
        if( r.left == left && r.right == right ) {
            maxx = max( maxx, r.max );
            minx = min( minx, r.min );
            return;
        }
        int mid = (r.left + r.right)/2;
        if( left > mid ) {
            query( 2*root+1,    left,   right,  maxx,   minx    );
        } else if( right <= mid ) {
            query( 2*root,      left,   right,  maxx,   minx    );
        } else {
            query( 2*root,      left,   mid,    maxx,   minx    );
            query( 2*root+1,    mid+1,  right,  maxx,   minx    );
        }
    }

    int n;
    vector<Node> node;
    vector<int> arr;
};

int main() {

    int n, q;
    while( 2 == scanf( "%d%d", &n, &q ) ) {

        IntervalTree it(n);
        for ( int i = 1; i <= n; ++i ) { scanf( "%d", &it.arr[i] ); }
        it.build( 1, 1, n );
        it.print();
        while ( q-- ) {
            int a, b;
            scanf( "%d%d", &a, &b );
            int maxx = -1, minx = 0x7FFFFFFF;
            it.query( 1, a, b, maxx, minx );
            printf("%d\n", maxx - minx );
        }
    }

    return 0;
}

compile & run:

# compile
$ g++ main.cpp
$ cat input.txt | ./a.out
A: [ 1 7 3 4 2 5 ].
1: [l: 1, r: 6, min: 1, max: 7]
2: [l: 1, r: 3, min: 1, max: 7]
3: [l: 4, r: 6, min: 2, max: 5]
4: [l: 1, r: 2, min: 1, max: 7]
5: [l: 3, r: 3, min: 3, max: 3]
6: [l: 4, r: 5, min: 2, max: 4]
7: [l: 6, r: 6, min: 5, max: 5]
8: [l: 1, r: 1, min: 1, max: 1]
9: [l: 2, r: 2, min: 7, max: 7]
12: [l: 4, r: 4, min: 4, max: 4]
13: [l: 5, r: 5, min: 2, max: 2]
6
3
0

refs and see also

exercise 1 @

#include <cstdio>
#include <vector>

using namespace std;

struct IntervalTree {
    struct Node {
        Node( int l = 0, int r = 0, int s = 0 ) : left(l), right(r), sum(s) {}
        int left, right, sum;
    };
    explicit IntervalTree( int n ) : n(n) {
        arr     =   vector<int>( n+1 );
        node    =   vector<Node>( 4*(n+1), Node() );
    }
    void build( int root, int left, int right ) {
        Node &r = node[root];
        r.left  = left;
        r.right = right;
        if( left == right ) {
            r.sum = arr[left];
            return;
        }
        int mid = (left+right)/2;
        build( 2*root,      left,       mid     );
        build( 2*root+1,    mid+1,      right   );
        r.sum = node[2*root].sum + node[2*root+1].sum;
    }

    void update( int root, int left, int right, int pos, int delta ) {
        Node &r = node[root];
        if( r.left > pos || r.right < pos ) { return; }
        if( r.left == r.right ) {
            r.sum += delta;
            return;
        }
        int mid = (r.left+r.right)/2;
        if( left > mid ) {
            update( 2*root+1,   left,   right,  pos,    delta   );
        } else if( right <= mid ) {
            update( 2*root,     left,   right,  pos,    delta   );
        } else {
            update( 2*root,     left,   mid,    pos,    delta   );
            update( 2*root+1,   mid+1,  right,  pos,    delta   );
        }
        r.sum = node[2*root].sum + node[2*root+1].sum;
    }

    int query( int root, int left, int right ) {
        Node &r = node[root];
        if( r.left == left && r.right == right ) {
            return r.sum;
        }
        int mid = (r.left + r.right)/2;
        if( left > mid ) {
            return query( 2*root+1, left, right );
        } else if( right <= mid ) {
            return query( 2*root,   left, right );
        } else {
            return query( 2*root, left, mid ) + query( 2*root+1, mid+1, right );
        }
    }

    int n;
    vector<Node> node;
    vector<int> arr;
};

int main() {

    int n, q;
    while( 1 == scanf( "%d", &n ) ) {

        IntervalTree it(n);
        for ( int i = 1; i <= n; ++i ) { scanf( "%d", &it.arr[i] ); }
        it.build( 1, 1, n );

        scanf( "%d", &q );
        while ( q-- ) {
            int cmd, a, b;
            scanf( "%d %d %d", &cmd, &a, &b );
            if( cmd == 2 ) {
                printf( "%d\n", it.query(1,a,b) );
            } else {
                if( b ) {
                    it.update( 1, 1, n, a, b );
                }
            }
        }
    }

    return 0;
}

input.txt:

6
4   5   6   2   1   3
4
1   3   5
2   1   4
1   1   9
2   2   6

$ g++ main.cpp
$ cat input.txt | ./a.out
22
22

A Simple Problem with Integers @

C   a   b   c           ->      A[i] += c, for i=[a..b]
Q   a   b               ->      sum of A[a..b]

#include <cstdio>
#include <vector>

using namespace std;

struct IntervalTree {
    struct Node {
        Node( int l = 0, int r = 0, int s = 0, int i = 0 ) : left(l), right(r), sum(s), inc(i) {}
        int left, right, sum, inc;                          // inc!
    };
    explicit IntervalTree( int n ) : n(n) {
        arr     =   vector<int>( n+1 );
        node    =   vector<Node>( 4*(n+1), Node() );
    }
    void build( int root, int left, int right ) {
        Node &r = node[root];
        r.left  = left;
        r.right = right;
        if( left == right ) {
            r.sum = arr[left];
            return;
        }
        int mid = (left+right)/2;
        build( 2*root,      left,       mid     );
        build( 2*root+1,    mid+1,      right   );
        r.sum = node[2*root].sum + node[2*root+1].sum;
    }

    void update( int root, int left, int right, int delta ) {
        Node &r = node[root];
        if( r.left == left && r.right == right ) {
            r.inc += delta;
            r.sum += delta * (right-left+1);
            return;
        }

        Node &nr = node[2*root+1];
        Node &nl = node[2*root];

        if( r.inc ) {
            nr.inc += r.inc;
            nl.inc += r.inc;
            nr.sum += r.inc * (nr.right-nr.left+1);
            nl.sum += r.inc * (nl.right-nl.left+1);
            r.inc = 0;
        }
        int mid = (r.left+r.right)/2;
        if( left > mid ) {
            update( 2*root+1,   left,   right,  delta   );
        } else if( right <= mid ) {
            update( 2*root,     left,   right,  delta   );
        } else {
            update( 2*root,     left,   mid,    delta   );
            update( 2*root+1,   mid+1,  right,  delta   );
        }
        r.sum = nr.sum + nl.sum;
    }

    int query( int root, int left, int right ) {
        Node &r = node[root];
        if( r.left == left && r.right == right ) {
            return r.sum;
        }

        Node &nr = node[2*root+1];
        Node &nl = node[2*root];

        if( r.inc ) {
            nr.inc += r.inc;
            nl.inc += r.inc;
            nr.sum += r.inc * (nr.right-nr.left+1);
            nl.sum += r.inc * (nl.right-nl.left+1);
            r.inc = 0;
        }
        int mid = (r.left + r.right)/2;
        if( left > mid ) {
            return query( 2*root+1, left, right );
        } else if( right <= mid ) {
            return query( 2*root,   left, right );
        } else {
            return query( 2*root, left, mid ) + query( 2*root+1, mid+1, right );
        }
    }

    int n;
    vector<Node> node;
    vector<int> arr;
};

int main() {

    int n, q;
    while( 2 == scanf( "%d %d", &n, &q ) ) {

        IntervalTree it(n);
        for ( int i = 1; i <= n; ++i ) { scanf( "%d", &it.arr[i] ); }
        it.build( 1, 1, n );

        while ( q-- ) {
            char buf[5];
            scanf( "%s", buf );
            int a, b, c;
            if( buf[0] == 'Q' ) {
                scanf( "%d %d", &a, &b );
                printf( "%d\n", it.query(1,a,b) );
            } else {
                scanf( "%d %d %d", &a, &b, &c );
                if( c ) { it.update(1, a, b, c ); }
            }
        }
    }

    return 0;
}

input.txt

10  5
1   2   3   4   5   6   7   8   9   10
Q   4   4
Q   1   10
Q   2   4
C   3   6   3
Q   2   4

$ cat input.txt | ./a.out
4
55
9
15

josephus problem ♥️ @

N = 8 children, count M, 1 <= N, M <= 30000

     1  2
   8      3
   7       4
     6  5

约瑟夫问题的难点在于，每一轮都不能通过简单的运算得出下一轮谁淘汰，因为中间有人已经退出了。因此一般只能模拟，效率很低。

现在考虑，每一轮都令所有剩下的人从左到右重新编号，例如 3 退出后，场上还剩下 1、2、4、5，则给

    1 新编号 1，
    2 新编号 2，
    4 新编号 3，
    5 新编号 4。

不妨称这个编号为“剩余队列编号”。如下所示，括号内为原始编号：

1(1) 2(2) 3(3) 4(4) 5(5)    --> 剩余队列编号 3 淘汰，对应原编号 3
1(1) 2(2) 3(4) 4(5)         --> 剩余队列编号 1 淘汰，对应原编号 1
1(2) 2(4) 3(5)              --> 剩余队列编号 3 淘汰，对应原编号 5
1(2) 2(4)                   --> 剩余队列编号 1 淘汰，对应原编号 2
1(4)                        --> 剩余队列编号 1 淘汰，对应原编号 4

一个人在当前剩余队列中编号为 i，则说明他是从左到右数第 i 个人，这启发我们可以用线段树来解决问题。用线段树维护原编号 [i..j] 内还有多少人没有被淘汰，这样每次选出被淘汰者后，在当前线段树中查找位置就可以了。

例如我们有 5 个原编号，当前淘汰者在剩余队列中编号为 3，先看左子树，即原编号 [1..3] 区间内，如果剩下的人不足 3 个，则说明当前剩余编号为 3 的这个人原编号只能是在 [4..5] 区间内，继续在 [4..5] 上搜索；如果 [1..3] 内剩下的人大于等于 3 个，则说明就在 [1..3] 内，也继续缩小范围查找，这样即可在 O(log N) 时间内完成对应。问题得到圆满的解决。

#include <cstdio>
#include <vector>

using namespace std;

struct IntervalTree {
    struct Node {
        Node( int l = 0, int r = 0, int c = 0 ) : left(l), right(r), count(c) {}
        int left, right, count;
    };
    explicit IntervalTree( int n ) : n(n) {
        node    =   vector<Node>( 4*(n+1), Node() );
    }
    void build( int root, int left, int right ) {
        Node &r = node[root];
        r.left  = left;
        r.right = right;
        r.count = right-left+1;
        if( left == right ) { return; }
        int mid = (left+right)/2;
        build( 2*root,      left,       mid     );
        build( 2*root+1,    mid+1,      right   );
    }

    int remove( int root, int i ) {
        Node &n = node[root]; --n.count;
        if( n.left == n.right ) {
            return n.left;
        }
        if( node[2*root].count >= i ) {
            return remove( 2*root, i );
        } else {
            return remove( 2*root+1, i-node[2*root].count );
        }
    }

    int getCount( int root, int i ) {
        if( node[root].right <= i ) { return node[root].count; }

        int mid = (node[root].left+node[root].right)/2;
        int s = 0;
        if( i > mid ) {
            s += node[2*root].count;
            s += getCount( 2*root+1, i );
        } else {
            s += getCount( 2*root,   i );
        }
        return s;
    }

    int n;
    vector<Node> node;
};

int main() {

    int n, m;
    while( 2 == scanf( "%d %d", &n, &m ) ) {

        IntervalTree it(n);
        it.build( 1, 1, n );
        int i, j = 0, k;
        for( i = 1; i <= n; ++i ) {
            j += m;
            if( j > it.node[1].count ) { j %= it.node[1].count; }
            if( j == 0    )            { j  = it.node[1].count; }
            k = it.remove(   1, j );
            j = it.getCount( 1, k );
            printf( "%d ", k );
        }

    }

    return 0;
}

$ echo 5 3 | ./a.out
3   1   5   2   4

✂️ 2016/08/29 上午 7:00:00 数据结构 Data Structure (下) @

Heap 的深入理解和运用

Heap 重要拓展： @

1. 带删除的堆 hash-heap

Trapping rain water @

: Trapping Rain Water | LeetCode OJ @

:   ![](http://www.leetcode.com/wp-content/uploads/2012/08/rainwatertrap.png)

    对于每个柱子，找到其左右两边最高的柱子，该柱子能容纳的面积就是 min(max_left, max_right) - height。所以，

    -   从左往右扫描一遍，对于每个柱子，求取左边最大值；
    -   从右往左扫描一遍，对于每个柱子，求最大右值；
    -   再扫描一遍，把每个柱子的面积并累加。

    也可以，

    -   扫描一遍，找到最高的柱子，这个柱子将数组分为两半；
    -   处理左边一半；
    -   处理右边一半。

    ```cpp
    // 没看懂，TODO
    class Solution {
    public:
        int trap(vector<int> &h) {
            int hl = 0, hr = 0, i = 0, j = h.size(), s = 0;
            while (i < j) {
                if (hl < hr) {
                    s += max(min(hl, hr)-h[i], 0);
                    hl = max(hl, h[i++]);
                } else {
                    s += max(min(hl, hr)-h[--j], 0);
                    hr = max(hr, h[j]);
                }
            }
            return s;
        }
    };
    ```

    ```cpp
    // 思路 1，时间复杂度 O(n)，空间复杂度 O(n)
    class Solution {
    public:
        int trap(const vector<int>& A) {
            if( n < 2 ) { return 0; }                               // 注意后面的 A[n-1] 一定要保证不越界啊！

            const int n = A.size();
            vector<int> max_left( n ), max_right( n );
            max_left[0] = A[0]; max_right[n-1] = A[n-1];
            for (int i = 1; i < n; i++ ) {
                max_left[i] = max(max_left[i - 1], A[i-1]);
                max_right[n-1-i] = max(max_right[n-i], A[n-i]);
            }

            int sum = 0;
            for (int i = 0; i < n; i++) {
                int height = min(max_left[i], max_right[i]);
                if (height > A[i]) {
                    sum += height - A[i];
                }
            }
            return sum;
        }
    };
    ```

    最推荐这个做法：

    ```cpp
    // 思路 2，时间复杂度 O(n)，空间复杂度 O(1)
    class Solution {
    public:
        int trap(const vector<int>& A) {
            const int n = A.size();
            int max = 0;                                    // 最高的柱子，将数组分为两半
            for (int i = 0; i < n; i++)
                if (A[i] > A[max]) max = i;

            int water = 0;
            for (int i = 0, peak = 0; i < max; i++)         // 左侧，从左往右直到 max
                if (A[i] > peak) peak = A[i];
                else water += peak - A[i];
            for (int i = n - 1, peak = 0; i > max; i--)      // 右侧，从右往左直到 max
                if (A[i] > peak) peak = A[i];
                else water += peak - A[i];
            return water;
        }
    };
    ```

    第三种解法，用一个栈辅助，小于栈顶的元素压入，大于
    等于栈顶就把栈里所有小于或等于当前值的元素全部出栈
    处理掉。（不推荐）

    ```cpp
    // 用一个栈辅助，小于栈顶的元素压入，大于等于栈顶就把栈里所有小于或
    // 等于当前值的元素全部出栈处理掉，计算面积，最后把当前元素入栈
    // 时间复杂度O(n)，空间复杂度O(n)
    class Solution {
    public:
        int trap(const vector<int>& A) {
            const int n = A.size();
            stack<pair<int, int>> s;
            int water = 0;

            for (int i = 0; i < n; ++i) {
                int height = 0;

                while (!s.empty()) { // 将栈里比当前元素矮或等高的元素全部处理掉
                    int bar = s.top().first;
                    int pos = s.top().second;
                    // bar, height, A[i] 三者夹成的凹陷
                    water += (min(bar, A[i]) - height) * (i - pos - 1);
                    height = bar;

                    if (A[i] < bar) // 碰到了比当前元素高的，跳出循环
                        break;
                    else
                        s.pop(); // 弹出栈顶，因为该元素处理完了，不再需要了
                }

                s.push(make_pair(A[i], i));
            }

            return water;
        }
    };
    ```

1. Building Outline

Median 问题拓展
Sliding Windows问题总结
双端队列Deque

✂️ 2016/09/04 上午 7:00:00 两个指针 Two Pointers @

对撞型指针
- 1. Two sum 类
- 1. Partition 类
前向型指针
- 1. 窗口类
- 1. 快慢类
两个数组上的指针

✂️ 2016/9/5 上午 7:00:00 动态规划 Dynamic Programming (上) @

记忆化搜索（区间动态规划、博弈类动态规划）
背包类动态规划
区间类动态规划

✂️ 2016/9/11 上午 7:00:00 动态规划 Dynamic Programming (下) @

记忆化搜索拓展
- 1. 区间动态规划
- 1. 博弈类动态规划
背包类动态规划
- 1. BackPack I/II
- 1. K sum
- 1. Minimum Adjustment Cost

✂️ 2016/9/12 上午 7:00:00 如何解决 follow up 问题 @

Peak Element I/II
第 K 大
- 1. 第 K 大
- 1. 有序矩阵的第 K 大
- 1. 两个数组乘积的第 K 大
- 1. n 个数组第 K 大
- 1. n 个数组多机第 K 大 (K 比较小)
- 1. n 个数组多机第 K 大 (K 比较大)
Subarray sum
- 1. Subarray sum
- 1. Submatrix sum
- 1. Subarray Sum Closest
- 1. Subarray sum II

✂️ 2016/00/00 上午 7:00:00 Math Methods and Models @

number theory
combination

10-1 UVa11582 Colossal Fibonacci Numbers! ch10/UVa11582.cpp @

// UVa11582 Colossal Fibonacci Numbers!
// Rujia Liu
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;

const int maxn = 1000 + 5;
typedef unsigned long long ULL;

int f[maxn][maxn*6], period[maxn];

int pow_mod(ULL a, ULL b, int n) {
    if(!b) return 1;
    int k = pow_mod(a, b/2, n);
    k = k * k % n;
    if(b % 2) k = k * a % n;
    return k;
}

int solve(ULL a, ULL b, int n) {
    if(a == 0 || n == 1) return 0; // attention!
    int p = pow_mod(a % period[n], b, period[n]);
    return f[n][p];
}

int main() {
    for(int n = 2; n <= 1000; n++) {
        f[n] = 0; f[n] = 1;
        for(int i = 2; ; i++) {
            f[n][i] = (f[n][i-1] + f[n][i-2]) % n;
            if(f[n][i-1] == 0 && f[n][i] == 1) {
                period[n] = i - 1;
                break;
            }
        }
    }
    ULL a, b;
    int n, T;
    cin >> T;
    while(T--) {
        cin >> a >> b >> n;
        cout << solve(a, b, n) << "\n";
    }
    return 0;
}

10-2 UVa12169 Disgruntled Judge ch10/UVa12169.cpp @

// UVa12169 Disgruntled Judge (slow solution)
// Rujia Liu
//
// rev2. fixed bug reported by EndlessCheng

#include<iostream>
using namespace std;

const int maxn = 100*2 + 5;
const int M = 10001;
int T, x[maxn];

void solve() {
    for(int a = 0; a < M; a++)
        for(int b = 0; b < M; b++) {
            bool ok = true;
            for(int i = 2; i <= T*2; i += 2) {
                x[i] = (a*x[i-1] + b) % M;
                if(i+1 <= T*2 && x[i+1] != (a*x[i] + b) % M) { ok = false; break; }
            }
            if(ok) return;
        }
}

int main () {
    while(cin >> T) {
        for(int i = 1; i <= T*2-1; i += 2) cin >> x[i];
        solve();
        for(int i = 2; i <= T*2; i += 2) cout << x[i] << "\n";
    }
    return 0;
}

10-3 UVa10375 Choose and Divide ch10/UVa10375.cpp @

// UVa10375 Choose and divide
// Rujia Liu
#include<cstdio>
#include<cstring>
#include<cmath>
#include<vector>
#include<iostream>
using namespace std;

const int maxn = 10000;
vector<int> primes;
int e[maxn];

// 乘以或除以n. d=0表示乘，d=-1表示除
void add_integer(int n, int d) {
    for(int i = 0; i < primes.size(); i++) {
        while(n % primes[i] == 0) {
            n /= primes[i];
            e[i] += d;
        }
        if(n == 1) break; // 提前终止循环，节约时间
    }
}

void add_factorial(int n, int d) {
    for(int i = 1; i <= n; i++)
        add_integer(i, d);
}

bool is_prime(int n) {
    int m = floor(sqrt(n) + 0.5);
    for(int a = 2; a <= m; a++)
        if(n % a == 0) return false;
    return true;
}

int main() {
    for(int i = 2; i <= 10000; i++)
        if(is_prime(i)) primes.push_back(i);
    int p, q, r, s;
    while(cin >> p >> q >> r >> s) {
        memset(e, 0, sizeof(e));
        add_factorial(p, 1);
        add_factorial(q, -1);
        add_factorial(p-q, -1);
        add_factorial(r, -1);
        add_factorial(s, 1);
        add_factorial(r-s, 1);
        double ans = 1;
        for(int i = 0; i < primes.size(); i++)
            ans *= pow(primes[i], e[i]);
        printf("%.5lf\n", ans);
    }
    return 0;
}

10-4 UVa10791 Minimum Sum LCM ch10/UVa10791.cpp @

// UVa10791 Minimum Sum LCM
// Rujia Liu
// 题意：输入整数n（1<=n<2^31），求至少两个正整数，使得它们的最小公倍数为n，且这些整数的和最小。输出最小的和。
// 算法：设唯一分解式n=a1^p1 * a2^p2...，不难发现每个a[i]^p[i]作为一个单独的整数时最优。
// 特例：n=1时答案为1+1=2。n只有一种因子时需要加个1。另外注意n=2^31-1时不要溢出
#include<cmath>
#include<iostream>
using namespace std;

int divide_all(int& n, int d) {
    int x = 1;
    while(n % d == 0) { n /= d; x *= d; }
    return x;
}

long long solve(int n) {
    if(n == 1) return 2;
    int m = floor(sqrt(n) + 0.5);
    long long ans = 0;
    int pf = 0; // 素因子(prime_factor)个数
    for(int i = 2; i < m; i++) {
        if(n % i == 0) { // 新的素因子
            pf++;
            ans += divide_all(n, i);
        }
    }
    if(n > 1) { pf++; ans += n; }
    if(pf <= 1) ans++;
    return ans;
}

int main() {
    int n, kase = 0;
    while(cin >> n && n)
        cout << "Case " << ++kase << ": " << solve(n) << "\n";
    return 0;
}

10-5 UVa12716 GCD XOR ch10/UVa12716.cpp @

// UVa12716 GCD XOR
// Rujia Liu

#include<cstdio>
#include<cstring>
using namespace std;

const int M = 30000000;
int cnt[M+1], sum[M+1];

void init() {
    memset(cnt, 0, sizeof(cnt));
    for(int c = 1; c <= M; c++)
        for(int a = c*2; a <= M; a += c) {
            int b = a - c;
            if(c == (a ^ b)) cnt[a]++;
        }
    sum = 0;
    for(int i = 1; i <= M; i++) sum[i] = sum[i-1] + cnt[i];
}

int main() {
    init();
    int T, n, kase = 0;
    scanf("%d", &T);
    while(T--) {
        scanf("%d", &n);
        printf("Case %d: %d\n", ++kase, sum[n]);
    }
    return 0;
}

10-6 UVa1635 Irrelevant Elements ch10/UVa1635.cpp @

// LA3221/UVa1635 Irrelevant Elements
// Rujia Liu
#include<cmath>
#include<iostream>
#include<vector>
#include<cstring>
using namespace std;

const int maxn = 100000 + 5;
int bad[maxn];

void prime_factors(int n, vector<int>& primes) {
    int m = floor(sqrt(n) + 0.5);
    for(int i = 2; i <= m; i++) {
        if(n % i == 0) { // 新的素因子
            primes.push_back(i);
            while(n % i == 0) n /= i;
        }
    }
    if(n > 1) primes.push_back(n);
}
int main() {
    int n, m, kase = 0;
    while(cin >> n >> m) {
        vector<int> primes;
        prime_factors(m, primes);
        memset(bad, 0, sizeof(bad));
        n--;
        // 求c(n,0)~c(n,n)有哪些数是m的倍数
        for(int i = 0; i < primes.size(); i++) {
            int p = primes[i], e = 0; // C(n,0) = p^e
            int min_e = 0, x = m;
            while(x % p == 0) { x /= p; min_e++; }
            // c(n,k)=c(n,k-1)*(n-k+1)/k
            for(int k = 1; k < n; k++) {
                x = n-k+1;
                while(x % p == 0) { x /= p; e++; }
                x = k;
                while(x % p == 0) { x /= p; e--; }
                if(e < min_e) bad[k] = 1;
            }
        }
        vector<int> ans;
        for(int k = 1; k < n; k++)
            if(!bad[k]) ans.push_back(k+1); // 编号从1开始
        cout << ans.size() << "\n";
        if(!ans.empty()) {
            cout << ans;
            for(int i = 1; i < ans.size(); i++) cout << " " << ans[i];
        }
        cout << "\n";
    }
    return 0;
}

10-7 UVa10820 Send a Table ch10/UVa10820.cpp @

// UVa10820 Send a Table
// Rujia Liu
#include<cstdio>
#include<cmath>
const int maxn = 50000;
int phi[maxn+1], phi_psum[maxn+1];

void phi_table(int n) {
    phi = 0;
    for(int i = 2; i <= n; i++) if(phi[i] == 0)
        for(int j = i; j <= n; j += i) {
            if(phi[j] == 0) phi[j] = j;
            phi[j] = phi[j] / i * (i-1);
        }
}

int main(){
    int n;
    phi_table(maxn);
    phi_psum = 0;
    for(int i = 1; i <= maxn; i++)
        phi_psum[i] = phi_psum[i-1] + phi[i];
    while(scanf("%d", &n) == 1 && n)
        printf("%d\n",2*phi_psum[n] + 1);
    return 0;
}

10-8 UVa1262 Password ch10/UVa1262.cpp @

// UVa1262 Password
// Rujia Liu
#include<cstdio>
#include<cstring>
using namespace std;

int k, cnt;
char p, ans;

// return true if already found
bool dfs(int col) {
    if(col == 5) {
        if(++cnt == k) {
            ans[col] = '\0';
            printf("%s\n", ans);
            return true;
        }
        return false;
    }
    bool vis;
    memset(vis, 0, sizeof(vis));
    for(int i = 0; i < 2; i++)
        for(int j = 0; j < 6; j++)
            vis[i][p[i][j][col] - 'A'] = true;
    for(int i = 0; i < 26; i++)
        if(vis[i] && vis[i]) {
            ans[col] = 'A' + i;
            if(dfs(col+1)) return true;
        }
    return false;
}

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        scanf("%d", &k);
        for(int i = 0; i < 2; i++)
            for(int j = 0; j < 6; j++)
                scanf("%s", p[i][j]);
        cnt = 0;
        if(!dfs(0)) printf("NO\n");
    }
    return 0;
}

10-9 UVa1636 Headshot ch10/UVa1636.cpp @

// UVa1636/LA4596 Headshot
// Rujia Liu
#include<cstdio>
#include<cstring>
int main() {
    char s;
    while(scanf("%s", s) == 1) {
        int a = 0, b = 0, n = strlen(s);
        for(int i = 0; i < n; i++) {
            if(s[i] == '0') {
                b++;
                if(s[(i+1)%n] == '0') a++;
            }
        }
        if(a*n == b*b) printf("EQUAL\n");
        else if(a*n > b*b) printf("SHOOT\n");
        else printf("ROTATE\n");
    }
    return 0;
}

10-10 UVa10491 Cows and Cars ch10/uva10491.cpp @

// UVa10491 Cows and Cars
// Rujia Liu
#include<cstdio>
int main() {
    int a, b, c;
    while(scanf("%d%d%d", &a, &b, &c) == 3)
        printf("%.5lf\n", (double)(a*b+b*(b-1)) / (a+b) / (a+b-c-1));
    return 0;
}

10-11 UVa11181 Probability|Given ch10/uva11181.cpp @

// UVa11181 Probability|Given
// Rujia Liu
#include<cstdio>
#include<cstring>
const int maxn = 20 + 5;
int n, r, buy[maxn];
double P[maxn], sum[maxn];

// depth, current number of 1, and product of probs
void dfs(int d, int c, double prob) {
    if(c > r || d - c > n - r) return; // too many 1/0
    if(d == n) {
        sum[n] += prob;
        for(int i = 0; i < n; i++) if(buy[i])
            sum[i] += prob;
        return;
    }
    buy[d] = 0;
    dfs(d+1, c, prob*(1-P[d]));
    buy[d] = 1;
    dfs(d+1, c+1, prob*P[d]);
}

int main() {
    int kase = 0;
    while(scanf("%d%d", &n, &r) == 2 && n) {
        for(int i = 0; i < n; i++) scanf("%lf", &P[i]);
        memset(sum, 0, sizeof(sum));
        dfs(0, 0, 1.0);
        printf("Case %d:\n", ++kase);
        for(int i = 0; i < n; i++)
            printf("%.6lf\n", sum[i] / sum[n]);
    }
    return 0;
}

10-12 UVa1637 Double Patience ch10/UVa1637.cpp @

// UVa1637 Double Patience
// Rujia Liu
#include<cstdio>
#include<vector>
#include<map>
using namespace std;

map<vector<int>, double> d;
char card;

// cnt is a vector of length 9, cnt[i] is the number of remaining cards in pile i.
// c is the sum of cnt. It is here to save time and code length :)
double dp(vector<int>& cnt, int c) {
    if(c == 0) return 1;
    if(d.count(cnt) != 0) return d[cnt];
    double sum = 0;
    int tot = 0;
    for(int i = 0; i < 9; i++) if(cnt[i] > 0)
        for(int j = i+1; j < 9; j++) if(cnt[j] > 0)
            if(card[i][cnt[i]-1] == card[j][cnt[j]-1]) {
                tot++;
                cnt[i]--; cnt[j]--;
                sum += dp(cnt, c-2);
                cnt[i]++; cnt[j]++;
            }
    if(tot == 0) return d[cnt] = 0;
    else return d[cnt] = sum / tot;
}

bool read_input() {
    for(int i = 0; i < 9; i++)
        for(int j = 0; j < 4; j++)
            if(scanf("%s", card[i][j]) != 1) return false;
    return true;
}

int main() {
    while(read_input()) {
        vector<int> cnt(9,4);
        d.clear();
        printf("%.6lf\n", dp(cnt, 36));
    }
    return 0;
}

10-13 UVa580 Critical Mass ch10/UVa580.cpp

// UVa580 Critical Mass
// Rujia Liu
#include<iostream>
using namespace std;

int f, g;

int main() {
    f = f = f = 0;
    g = 1; g = 2; g = 4;
    for(int n = 3; n <= 30; n++) {
        f[n] = 1 << (n-3);
        for(int i = 2; i <= n-2; i++)
            f[n] += g[i-2] * (1 << (n-i-2));
        g[n] = (1<<n) - f[n];
    }
    int n;
    while(cin >> n && n)
        cout << f[n] << "\n";
    return 0;
}

10-14 UVa12034 Race ch10/UVa12034.cpp

// UVa12034 Race
// Rujia Liu
#include<cstdio>

const int maxn = 1000;
const int MOD = 10056;
int C[maxn+1][maxn+1], f[maxn+1];

// 递推出所有组合数
void init() {
    for(int i = 0; i <= maxn; i++) {
        C[i] = C[i][i] = 1;
        for(int j = 1; j < i; j++)
            C[i][j] = (C[i-1][j] + C[i-1][j-1]) % MOD;
    }
}

int main() {
    init();
    f = 1;
    for(int i = 1; i <= maxn; i++) {
        f[i] = 0;
        for(int j = 1; j <= i; j++) f[i] = (f[i] + C[i][j] * f[i-j]) % MOD;
    }

    int T, n;
    scanf("%d", &T);
    for(int kase = 1; kase <= T; kase++) {
        scanf("%d", &n);
        printf("Case %d: %d\n", kase, f[n]);
    }
    return 0;
}

10-15 UVa1638 Pole Arrangement ch10/UVa1638.cpp @

// UVa1638/LA6117 Pole Arrangement
// Rujia Liu
#include<iostream>
using namespace std;

const int maxn = 20;
long long d[maxn+1][maxn+1][maxn+1];

int main() {
    d = 1;
    for(int i = 2; i <= maxn; i++)
        for(int j = 1; j <= i; j++)
            for(int k = 1; k <= i; k++) {
                d[i][j][k] = d[i-1][j][k] * (i-2);
                if(j > 1) d[i][j][k] += d[i-1][j-1][k];
                if(k > 1) d[i][j][k] += d[i-1][j][k-1];
            }

    int T, n, L, R;
    cin >> T;
    while(T--) {
        cin >> n >> L >> R;
        cout << d[n][L][R] << "\n";
    }
    return 0;
}

10-16 UVa12230 Crossing Rivers ch10/uva12230.cpp @

// UVa12230 Crossing Rivers
// Rujia Liu
#include<cstdio>
int main() {
    int n, D, p, L, v, kase = 0;
    while(scanf("%d%d", &n, &D) == 2 && D) {
        double ans = 0;
        while(n--) {
            scanf("%d%d%d", &p, &L, &v);
            D -= L; ans += 2.0 * L / v;
        }
        printf("Case %d: %.3lf\n\n", ++kase, ans + D);
    }
    return 0;
}

10-17 UVa1639 Candy ch10/UVa1639.cpp

// UVa1639/LA6163 Candy
// Rujia Liu
#include<cstdio>
#include<cmath>
// C(n,m) = n!/(m!(n-m)!)
const int maxn = 200000 + 5;
long double logF[maxn*2+1];

long double logC(int n, int m) {
    return logF[n] - logF[m] - logF[n-m];
}

double solve(int n, double p) {
    double ans = 0;
    for(int i = 0; i <= n; i++) {
        long double c = logC(n*2-i, n);
        long double v1 = c + (n+1)*log(p) + (n-i)*log(1-p);
        long double v2 = c + (n+1)*log(1-p) + (n-i)*log(p);
        long double x = exp(v1) + exp(v2);
        ans += i * (exp(v1) + exp(v2));
    }
    return ans;
}

int main() {
    logF = 0;
    for(int i = 1; i <= maxn; i++)
        logF[i] = logF[i-1] + log(i);

    int kase = 0, n;
    double p;
    while(scanf("%d%lf", &n, &p) == 2)
        printf("Case %d: %.6lf\n", ++kase, solve(n, p));
    return 0;
}

10-18 UVa10288 Coupons ch10/UVa10288.cpp @

// UVa10288 Coupons
// Rujia Liu
#include<iostream>
#include<sstream>
using namespace std;

typedef long long LL;

LL gcd(LL a, LL b) {
    if(!b) return a;
    return gcd(b, a%b);
}

LL lcm(LL a, LL b) {
    return a / gcd(a, b) * b;
}

int LL_len(LL x) {
    stringstream ss;
    ss << x;
    return ss.str().length();
}

void print_chars(int cnt, char ch) {
    while(cnt--) cout << ch;
}

void output(LL a, LL b, LL c) {
    if(b == 0) cout << a << "\n";
    else {
        int L1 = LL_len(a);
        print_chars(L1+1, ' '); cout << b << "\n";
        cout << a << " "; print_chars(LL_len(c), '-'); cout << "\n";
        print_chars(L1+1, ' '); cout << c << "\n";
    }
}

int main() {
    int n;
    while(cin >> n && n) {
        if(n == 1) { output(1, 0, 0); continue; }
        LL x = 1;
        for(int i = 2; i <= n-1; i++)
            x = lcm(x, i);

        // b/c = 1/(n-1) + ... + 1/2
        LL c = x, b = 0;
        for(int i = 2; i <= n-1; i++)
            b += x / i;
        b *= n;
        LL g = gcd(b, c);
        b /= g; c /= g;

        // ans = a + b/c
        LL a = 1 + n + b / c;
        b %= c;
        output(a, b, c);
    }
    return 0;
}

10-19 UVa11346 Probability ch10/uva11346.cpp @

// UVa11346 Probability
// Rujia Liu
#include<cstdio>
#include<cmath>
int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        double a, b, s, ans;
        scanf("%lf%lf%lf", &a, &b, &s);
        double m = a*b;
        if(fabs(s) < 1e-6) ans = 1;
        else if(s > m) ans = 0;
        else ans = (m - s - s * log(m/s)) / m;
        printf("%.6lf%%\n", ans * 100);
    }
    return 0;
}

10-20 UVa10900 So you want to be a 2n-aire? ch10/UVa10900.cpp @

// UVa10900 So you want to be a 2n-aire?
// Rujia Liu
#include<cstdio>
using namespace std;

const int maxn = 30 + 5;
double d[maxn];

int main() {
    int n;
    double t;
    while(scanf("%d%lf", &n, &t) == 2 && n) {
        d[n] = 1<<n;
        for(int i = n-1; i >= 0; i--) {
            double p0 = (double)(1<<i) / d[i+1];
            if(p0 < t) p0 = t;
            double p1 = (p0-t)/(1-t);
            d[i] = (double)(1<<i) * p1 + (1+p0)/2 * d[i+1] * (1-p1);
        }
        printf("%.3lf\n", d);
    }
    return 0;
}

10-21 UVa11971 Polygon ch10/UVa11971.cpp @

// UVa11971 Polygon
// Rujia Liu
#include<iostream>
using namespace std;

typedef long long LL;

LL gcd(LL a, LL b) {
    return b == 0 ? a : gcd(b, a%b);
}

void reduce(LL& a, LL& b) {
    LL g = gcd(a, b);
    a /= g; b /= g;
}

int main() {
    int T, n, k;
    cin >> T;
    for(int kase = 1; kase <= T; kase++) {
        cin >> n >> k;
        // 组不成的概率为(k+1)/2^k
        LL b = 1LL << k;
        LL a = b - k - 1;
        reduce(a, b);
        cout << "Case #" << kase << ": " << a << "/" << b << endl;
    }
    return 0;
}

10-22 UVa1640 The Counting Problem ch10/UVa1640.cpp @

// UVa1640 The Counting Problem
// Rujia Liu
// The meaning of f is slightly different from the book
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

// cnt[i] is the number of occurrence of EVERY digit, among all i-digit numbers (leading zeros ALLOWED)
// for examples, there are 1000 3-digit numbers, each digit 0~9 has occurred 300 times, so cnt = 300
int pow10, cnt;

// how many times digit d occurred in 0~n-1
// numbers in 0~4567 can be divided into the following patterns:
// fewer digits   : *, n*, n** (n means non-zero digit)
// smaller digit 0: 1***, 2***, 3***
// smaller digit 1: 40**, 41**, 42**, 43**, 44**
// smaller digit 2: 450*, 451*, ...
int f(int d, int n) {
    char s;
    sprintf(s, "%d", n);
    int len = strlen(s);
    int ans = 0;

    // fewer digits
    for(int i = 1; i < len; i++) {
        if(i == 1) ans++; // single digit
        else {
            ans += 9 * cnt[i-1];  // leading with another digit
            if(d > 0) ans += pow10[i-1]; // leading with digit d
        }
    }

    int pre; // pre[i] is the occurrence of digit d in s[0~i]
    for(int i = 0; i < len; i++) {
        pre[i] = (s[i] - '0' == d ? 1 : 0);
        if(i > 0) pre[i] += pre[i-1];
    }

    for(int i = 0; i < len; i++) {
        // smaller digit i
        int maxd = s[i] - '0' - 1;
        int mind = 0;
        if(i == 0 && len > 1) mind = 1; // no leading zeros allowed
        for(int digit = mind; digit <= maxd; digit++) {
            ans += cnt[len-i-1];
            if(i > 0) ans += pre[i-1] * pow10[len-i-1];
            if(digit == d) ans += pow10[len-i-1];
        }
    }
    return ans;
}

int main() {
    pow10 = 1;
    for(int i = 1; i <= 8; i++) {
        pow10[i] = pow10[i-1] * 10;
        cnt[i] = pow10[i-1] * i;
    }

    int a, b;
    while(scanf("%d%d", &a, &b) == 2 && a && b) {
        if(a > b) swap(a, b);
        for(int d = 0; d < 10; d++) {
            if(d) printf(" ");
            printf("%d", f(d, b+1) - f(d, a));
        }
        printf("\n");
    }
    return 0;
}

10-23 UVa10213 How Many Pieces of Land? ch10/UVa10213.cpp @

// UVa10213 How Many Pieces of Land?
// Rujia Liu
#include<cstdio>
int main() {
    int n, T;
    scanf("%d", &T);
    while(T--) {
        scanf("%d", &n);
        int V = 0, E = 0;
        for(int i = 0; i <= n-2; i++)
            V += i*(n-2-i), E += i*(n-2-i)+1;
        V = V*n/4+n;
        E = E*n/2+n;
        printf("%d\n", E-V+1);
    }
    return 0;
}

10-24 UVa1641 ASCII Area ch10/UVa1641.cpp @

// UVa1641/LA5910 ASCII Area
// Rujia Liu
#include<cstdio>
int main() {
    int h, w;
    char s;
    while(scanf("%d%d", &h, &w) == 2) {
        int ans = 0, c = 0;
        while(h--) {
            scanf("%s", s);
            int in = 0;
            for(int i = 0; i < w; i++) {
                if(s[i] == '/' || s[i] == '\\') { c++; in = !in; }
                else if(in) ans++;
            }
        }
        printf("%d\n", ans + c/2);
    }
    return 0;
}

10-25 UVa1363 Joseph’s Problem ch10/UVa1363.cpp @

// UVa1363 Joseph's Problem
// Rujia Liu
#include<iostream>
#include<algorithm>
using namespace std;

// 首项为a，公差为-d，除了首项之外还有n项
// 末项为a-n*d，平均数为(2*a-n*d)/2
long long sum(int a, int d, int n) {
    return (long long)(2*a-n*d)*(n+1)/2;
}

int main() {
    int n, k;
    while(cin >> n >> k) {
        int i = 1;
        long long ans = 0;
        while(i <= n) {
            int q = k % i, p = k / i;
            int cnt = n - i; // 最多还有n - i项
            if(p > 0) cnt = min(cnt, q / p);
            ans += sum(q, p, cnt);
            i += cnt + 1;
        }
        cout << ans << "\n";
    }
    return 0;
}

10-26 UVa11440 Help Mr. Tomisu ch10/UVa11440.cpp @

// UVa11440 Help Mr. Tomisu
// Rujia Liu
#include<cstdio>
#include<cmath>
#include<cstring>
const int maxn = 10000000 + 10;
const int MOD = 100000007;

int vis[maxn], phifac[maxn];

void gen_primes(int n) {
    int m = (int)sqrt(n+0.5);
    int c = 0;
    memset(vis, 0, sizeof(vis));
    for(int i = 2; i <= m; i++) if(!vis[i]) {
        for(int j = i*i; j <= n; j+=i) vis[j] = 1;
    }
}

int main() {
    int n, m;
    gen_primes(10000000);
    phifac = phifac = 1;
    for(int i = 3; i <= 10000000; i++)
        phifac[i] = (long long)phifac[i-1] * (vis[i] ? i : i-1) % MOD;

    while(scanf("%d%d", &n, &m) == 2 && n) {
        int ans = phifac[m];
        for(int i = m+1; i <= n; i++) ans = (long long)ans * i % MOD;
        printf("%d\n", (ans-1+MOD)%MOD);
    }
    return 0;
}

10-27 UVa10214 Trees in a Wood ch10/UVa10214.cpp @

// UVa10214 Trees in a Wood
// Rujia Liu
// This problem asks for K/N, where N is the total number of trees in area |x|<=a, |y|<=b
// The answer converges to 6/pi^2, see the problem description
#include<cstdio>
#include<cmath>
using namespace std;

int phi(int n) {
    int m = (int)sqrt(n+0.5);
    int ans = n;
    for(int i = 2; i <= m; i++) if(n % i == 0) {
        ans = ans / i * (i-1);
        while(n % i == 0) n /= i;
    }
    if(n > 1) ans = ans / n * (n-1);
    return ans;
}

int gcd(int a, int b) {
    return b == 0 ? a : gcd(b, a % b);
}

long long f(int a, int b) {
    long long ans = 0; // only for 1<=x<=a, 1<=y<=b
    for(int x = 1; x <= a; x++) {
        int k = b/x;
        ans += phi(x) * k;
        for(int y = k*x+1; y <= b; y++)
            if(gcd(x, y) == 1) ans++;
    }
    return ans * 4 + 4;
}

int main() {
    int a, b;
    while(scanf("%d%d", &a, &b) == 2 && a) {
        long long K = f(a,b);
        long long N = (long long)(2*a+1) * (2*b+1) - 1;
        printf("%.7lf\n", (double)K / N);
    }
    return 0;
}

10-28 UVa1393 Highway ch10/uva1393.cpp @

// UVa1393 Highway
// Rujia Liu
#include<iostream>
#include<algorithm>
using namespace std;

const int maxn = 300;
int g[maxn+1][maxn+1];

int gcd(int a, int b) {
    return b == 0 ? a : gcd(b, a%b);
}

int main() {
    int n, m;
    for(int i = 1; i <= maxn; i++)
        for(int j = 1; j <= maxn; j++)
            g[i][j] = gcd(i, j);

    while(cin >> n >> m && n) {
        int ans = 0;
        for(int a = 1; a <= m; a++)
            for(int b = 1; b <= n; b++)
                if(g[a][b] == 1) {
                    int c = max(0, m-2*a) * max(0, n-2*b);
                    ans += (m-a)*(n-b) - c;
                }
        cout << ans*2 << "\n";
    }
    return 0;
}

10-29 UVa1642 Magical GCD ch10/UVa1642.cpp @

// UVa1642 Magical GCD
// Rujia Liu
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;

typedef long long LL;

struct Item {
    LL g; // gcd
    int p; // starting pos
    Item(LL g=0, int p=0):g(g),p(p){}
    bool operator < (const Item& rhs) const {
        return g < rhs.g || (g == rhs.g && p < rhs.p);
    }
};

LL gcd(LL a, LL b) { return b == 0 ? a : gcd(b, a%b); }

const int maxn = 100000 + 5;

LL A[maxn];
int n;

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        scanf("%d", &n);
        for(int i = 0; i < n; i++) scanf("%lld", &A[i]);
        vector<Item> items;
        LL ans = 0;
        for(int j = 0; j < n; j++) { // enumerate end pos
            items.push_back(Item(0, j));
            for(int k = 0; k < items.size(); k++)
                items[k].g = gcd(items[k].g, A[j]); // update items' gcd
            sort(items.begin(), items.end());

            // for each gcd, only keep smallest starting pos
            vector<Item> newitems;
            for(int k = 0; k < items.size(); k++)
                if(k == 0 || items[k].g != items[k-1].g) { // different gcd
                    newitems.push_back(items[k]);
                    ans = max(ans, items[k].g * (j - items[k].p + 1));
                }
            items = newitems;
        }
        printf("%lld\n", ans);
    }
    return 0;
}

11-1 UVa12219 Common Subexpression Elimination ch11/UVa12219.cpp @

// UVa12219 Common Subexpression Elimination
// Rujia Liu

#include<cstdio>
#include<string>
#include<map>
using namespace std;

const int maxn = 60000;
int T, kase, cnt;
char expr[maxn*5], *p;
int done[maxn]; // 该结点是否已输出

struct Node {
    string s;
    int hash, left, right;
    bool operator < (const Node& rhs) const {
        if(hash != rhs.hash) return hash < rhs.hash;
        if(left != rhs.left) return left < rhs.left;
        return right < rhs.right;
    }
} node[maxn];

map<Node,int> dict;

int parse() {
    int id = cnt++;
    Node& u = node[id];
    u.left = u.right = -1;
    u.s = "";
    u.hash = 0;
    while(isalpha(*p)) {
        u.hash = u.hash * 27 + *p - 'a' + 1;
        u.s.push_back(*p);
        p++;
    }
    if (*p == '(') { // (L,R)
        p++; u.left = parse(); p++; u.right = parse(); p++;
    }
    if (dict.count(u) != 0) {
        id--; cnt--;
        return dict[u];
    }
    return dict[u] = id;
}

void print(int v) {
    if(done[v] == kase)
        printf("%d", v + 1);
    else {
        done[v] = kase; // 常见小技巧，可以避免memset(done, 0, sizeof(done))
        printf("%s", node[v].s.c_str());
        if(node[v].left != -1) {
            putchar('(');
            print(node[v].left);
            putchar(',');
            print(node[v].right);
            putchar(')');
        }
    }
}

int main() {
    scanf("%d", &T);
    for(kase = 1; kase <= T; kase++) {
        dict.clear();
        cnt = 0;
        scanf("%s", expr);
        p = expr;
        print(parse());
        putchar('\n');
    }
    return 0;
}

11-2 UVa1395 Slim Span ch11/UVa1395.cpp @

// UVa1395 Slim Span
// Rujia Liu
#include<cstdio>
#include<cmath>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;

const int maxn = 100 + 10;
const int INF = 1000000000;
int n;

int pa[maxn];
int findset(int x) { return pa[x] != x ? pa[x] = findset(pa[x]) : x; }

struct Edge {
    int u, v, d;
    Edge(int u, int v, int d):u(u),v(v),d(d) {}
    bool operator < (const Edge& rhs) const {
        return d < rhs.d;
    }
};

vector<Edge> e;

int solve() {
    int m = e.size();
    sort(e.begin(), e.end());
    int ans = INF;
    for(int L = 0; L < m; L++) {
        for(int i = 1; i <= n; i++) pa[i] = i;
        int cnt = n; // number of sets
        for(int R = L; R < m; R++) {
            int u = findset(e[R].u), v = findset(e[R].v);
            if(u != v) {
                pa[u] = v;
                if(--cnt == 1) { ans = min(ans, e[R].d-e[L].d); break; }
            }
        }
    }
    if(ans == INF) ans = -1;
    return ans;
}

int main() {
    int m, u, v, d;
    while(scanf("%d%d", &n, &m) == 2 && n) {
        e.clear();
        for(int i = 0; i < m; i++) {
            scanf("%d%d%d", &u, &v, &d);
            e.push_back(Edge(u, v, d));
        }
        printf("%d\n", solve());
    }
    return 0;
}

11-3 UVa1151 Buy or Build ch11/UVa1151.cpp @

// UVa1151 Buy or Build
// Rujia Liu
#include<cstdio>
#include<cmath>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;

const int maxn = 1000 + 10;
const int maxq = 8;
int n;
int x[maxn], y[maxn], cost[maxq];
vector<int> subn[maxq];

int pa[maxn];
int findset(int x) { return pa[x] != x ? pa[x] = findset(pa[x]) : x; }

struct Edge {
    int u, v, d;
    Edge(int u, int v, int d):u(u),v(v),d(d) {}
    bool operator < (const Edge& rhs) const {
        return d < rhs.d;
    }
};

// initialize pa and sort e before calling this method
// cnt is the current number of components
int MST(int cnt, const vector<Edge>& e, vector<Edge>& used) {
    if(cnt == 1) return 0;
    int m = e.size();
    int ans = 0;
    used.clear();
    for(int i = 0; i < m; i++) {
        int u = findset(e[i].u), v = findset(e[i].v);
        int d = e[i].d;
        if(u != v) {
            pa[u] = v;
            ans += d;
            used.push_back(e[i]);
            if(--cnt == 1) break;
        }
    }
    return ans;
}

int main() {
    int T, q;
    scanf("%d", &T);
    while(T--) {
        scanf("%d%d", &n, &q);
        for(int i = 0; i < q; i++) {
            int cnt;
            scanf("%d%d", &cnt, &cost[i]);
            subn[i].clear();
            while(cnt--) {
                int u;
                scanf("%d", &u);
                subn[i].push_back(u-1);
            }
        }
        for(int i = 0; i < n; i++) scanf("%d%d", &x[i], &y[i]);

        vector<Edge> e, need;
        for(int i = 0; i < n; i++)
            for(int j = i+1; j < n; j++) {
                int c = (x[i]-x[j])*(x[i]-x[j]) + (y[i]-y[j])*(y[i]-y[j]);
                e.push_back(Edge(i, j, c));
            }

        for(int i = 0; i < n; i++) pa[i] = i;
        sort(e.begin(), e.end());

        int ans = MST(n, e, need);
        for(int mask = 0; mask < (1<<q); mask++) {
            // union cities in the same sub-network
            for(int i = 0; i < n; i++) pa[i] = i;
            int cnt = n, c = 0;
            for(int i = 0; i < q; i++) if(mask & (1<<i)) {
                c += cost[i];
                for(int j = 1; j < subn[i].size(); j++) {
                    int u = findset(subn[i][j]), v = findset(subn[i]);
                    if(u != v) { pa[u] = v; cnt--; }
                }
            }
            vector<Edge> dummy;
            ans = min(ans, c + MST(cnt, need, dummy));
        }
        printf("%d\n", ans);
        if(T) printf("\n");
    }
    return 0;
}

11-4 UVa247 Calling Circles ch11/UVa247.cpp @

// UVa247 Calling Circles
// Rujia Liu
#include<cstdio>
#include<vector>
#include<string>
#include<map>
#include<cstring>
using namespace std;

vector<string> names;
int ID(const string& s) {
    for(int i = 0; i < names.size(); i++)
        if(names[i] == s) return i;
    names.push_back(s);
    return names.size() - 1;
}

const int maxn = 25 + 5;
int n, m, vis[maxn], d[maxn][maxn];
void dfs(int u) {
    vis[u] = 1;
    for(int v = 0; v < n; v++)
        if(!vis[v] && d[u][v] && d[v][u]) {
            printf(", %s", names[v].c_str());
            dfs(v);
        }
}

int main() {
    char s1, s2;
    int kase = 0;
    while(scanf("%d%d", &n, &m) == 2 && n) {
        names.clear();
        memset(d, 0, sizeof(d));
        for(int i = 0; i < n; i++) d[i][i] = 1;
        while(m--) {
            scanf("%s%s", s1, s2);
            d[ID(s1)][ID(s2)] = 1;
        }
        for(int k = 0; k < n; k++)
            for(int i = 0; i < n; i++)
                for(int j = 0; j < n; j++)
                    d[i][j] |= d[i][k] && d[k][j];

        if(kase > 0) printf("\n");
        printf("Calling circles for data set %d:\n", ++kase);

        memset(vis, 0, sizeof(vis));
        for(int i = 0; i < n; i++)
            if(!vis[i]) {
                printf("%s", names[i].c_str());
                dfs(i);
                printf("\n");
            }
    }
    return 0;
}

11-5 UVa10048 Audiophobia ch11/UVa10048.cpp @

// UVa10048 Audiophobia
// Rujia Liu
// 题意：输入一个无项带权图，回答一些询问，询问内容是问某两点间最大权最小的路径
// 算法：变形的floyd
#include<cstdio>
#include<algorithm>
using namespace std;

const int maxn = 100 + 5;
const int INF = 1000000000;
int d[maxn][maxn];

int main() {
    int n, m, Q, u, v, w, kase = 0;
    while(scanf("%d%d%d", &n, &m, &Q) == 3 && n) {
        // 初始化
        for(int i = 0; i < n; i++) {
            d[i][i] = 0;
            for(int j = i+1; j < n; j++) { d[i][j] = d[j][i] = INF; }
        }
        for(int i = 0; i < m; i++) {
            scanf("%d%d%d", &u, &v, &w); u--; v--;
            d[u][v] = min(d[u][v], w);
            d[v][u] = d[u][v];
        }
        // 主算法
        for(int k = 0; k < n; k++)
            for(int i = 0; i < n; i++)
                for(int j = 0; j < n; j++)
                    if(d[i][k] < INF && d[k][j] < INF)
                        d[i][j] = min(d[i][j], max(d[i][k], d[k][j]));
        // 询问
        if(kase) printf("\n");
        printf("Case #%d\n", ++kase);
        while(Q--) {
            scanf("%d%d", &u, &v); u--; v--;
            if(d[u][v] == INF) printf("no path\n"); else printf("%d\n", d[u][v]);
        }
    }
    return 0;
}

11-6 UVa658 It’s not a Bug, it’s a Feature! ch11/UVa658.cpp @

// UVa658 It's not a Bug, it's a Feature!
// Rujia Liu
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;

struct Node {
    int bugs, dist;
    bool operator < (const Node& rhs) const {
        return dist > rhs.dist;
    }
};

const int maxn = 20;
const int maxm = 100 + 5;
const int INF = 1000000000;

int n, m, t[maxm], dist[1<<maxn], mark[1<<maxn];
char before[maxm][maxn + 5], after[maxm][maxn + 5];

int solve() {
    for(int i = 0; i < (1<<n); i++) { mark[i] = 0; dist[i] = INF; }
    priority_queue<Node> q;

    Node start;
    start.dist = 0;
    start.bugs = (1<<n) - 1;
    q.push(start);

    dist[start.bugs] = 0;
    while(!q.empty()) {
        Node u = q.top(); q.pop();
        if(u.bugs == 0) return u.dist;
        if(mark[u.bugs]) continue;
        mark[u.bugs] = 1;
        for(int i = 0; i < m; i++) {
            bool patchable = true;
            for(int j = 0; j < n; j++) {
                if(before[i][j] == '-' && (u.bugs & (1<<j))) { patchable = false; break; }
                if(before[i][j] == '+' && !(u.bugs & (1<<j))) { patchable = false; break; }
            }
            if(!patchable) continue;

            Node u2;
            u2.dist = u.dist + t[i];
            u2.bugs = u.bugs;
            for(int j = 0; j < n; j++) {
                if(after[i][j] == '-') u2.bugs &= ~(1<<j);
                if(after[i][j] == '+') u2.bugs |= (1<<j);
            }
            int& D = dist[u2.bugs];
            if(D < 0 || u2.dist < D) {
                D = u2.dist;
                q.push(u2);
            }
        }
    }
    return -1;
}

int main() {
    int kase = 0;
    while(scanf("%d%d", &n, &m) == 2 && n) {
        for(int i = 0; i < m; i++) scanf("%d%s%s", &t[i], before[i], after[i]);
        int ans = solve();
        printf("Product %d\n", ++kase);
        if(ans < 0) printf("Bugs cannot be fixed.\n\n");
        else printf("Fastest sequence takes %d seconds.\n\n", ans);
    }
    return 0;
}

11-7 UVa753 A Plug for UNIX ch11/UVa753.cpp UVa753b.cpp @

// UVa753 A Plug for UNIX
// Rujia Liu
// 算法一：先做一次floyd，然后再构图
#include<iostream>
#include<map>
#include<string>
#include<vector>
#include<cstring>
#include<queue>
using namespace std;

vector<string> names;
int ID(const string& s) {
    for(int i = 0; i < names.size(); i++)
        if(names[i] == s) return i;
    names.push_back(s);
    return names.size() - 1;
}

const int maxn = 400 + 5;

int n, m, k;       // 插座个数，设备个数，转换器个数
int d[maxn][maxn]; // d[i][j]=1表示插头类型i可以转化为插头类型j
int target[maxn];  // 各个插座的类型
int device[maxn];  // 各个设备的类型

const int INF = 1000000000;

struct Edge {
    int from, to, cap, flow;
    Edge(int u, int v, int c, int f):from(u),to(v),cap(c),flow(f) {}
};

struct EdmondsKarp {
    int n, m;
    vector<Edge> edges;    // 边数的两倍
    vector<int> G[maxn];   // 邻接表，G[i][j]表示结点i的第j条边在e数组中的序号
    int a[maxn];           // 当起点到i的可改进量
    int p[maxn];           // 最短路树上p的入弧编号

    void init(int n) {
        for(int i = 0; i < n; i++) G[i].clear();
        edges.clear();
    }

    void AddEdge(int from, int to, int cap) {
        edges.push_back(Edge(from, to, cap, 0));
        edges.push_back(Edge(to, from, 0, 0));
        m = edges.size();
        G[from].push_back(m-2);
        G[to].push_back(m-1);
    }

    int Maxflow(int s, int t) {
        int flow = 0;
        for(;;) {
            memset(a, 0, sizeof(a));
            queue<int> Q;
            Q.push(s);
            a[s] = INF;
            while(!Q.empty()) {
                int x = Q.front(); Q.pop();
                for(int i = 0; i < G[x].size(); i++) {
                    Edge& e = edges[G[x][i]];
                    if(!a[e.to] && e.cap > e.flow) {
                        p[e.to] = G[x][i];
                        a[e.to] = min(a[x], e.cap-e.flow);
                        Q.push(e.to);
                    }
                }
                if(a[t]) break;
            }
            if(!a[t]) break;
            for(int u = t; u != s; u = edges[p[u]].from) {
                edges[p[u]].flow += a[t];
                edges[p[u]^1].flow -= a[t];
            }
            flow += a[t];
        }
        return flow;
    }
};

EdmondsKarp g;

int main() {
    int T;
    cin >> T;
    while(T--) {
        names.clear();
        string s1, s2;
        cin >> n;
        for(int i = 0; i < n; i++) {
            cin >> s1;
            target[i] = ID(s1);
        }
        cin >> m;
        for(int i = 0; i < m; i++) {
            cin >> s1 >> s2;
            device[i] = ID(s2);
        }
        cin >> k;
        memset(d, 0, sizeof(d));
        for(int i = 0; i < k; i++) {
            cin >> s1 >> s2;
            d[ID(s1)][ID(s2)] = 1;
        }
        // floyd
        int V = names.size(); // 插头类型个数
        for(int k = 0; k < V; k++)
            for(int i = 0; i < V; i++)
                for(int j = 0; j < V; j++)
                    d[i][j] |= d[i][k] && d[k][j];

        g.init(V+2);
        for(int i = 0; i < m; i++)
            g.AddEdge(V, device[i], 1); // 源点->设备
        for(int i = 0; i < n; i++)
            g.AddEdge(target[i], V+1, 1); // 插座->汇点

        for(int i = 0; i < m; i++)
            for(int j = 0; j < n; j++)
                if(d[device[i]][target[j]]) g.AddEdge(device[i], target[j], INF); // 设备->插座
        int r = g.Maxflow(V, V+1);
        cout << m-r << "\n";
        if(T) cout << "\n";
    }
    return 0;
}

11-8 UVa11082 Matrix Decompressing ch11/UVa11082.cpp @

// UVa11082 Matrix Decompressing
// Rujia Liu
// Slower version with EdmondsKarp
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
#include<algorithm>
using namespace std;

const int maxn = 50 + 5;
const int INF = 1000000000;

struct Edge {
    int from, to, cap, flow;
    Edge(int u, int v, int c, int f):from(u),to(v),cap(c),flow(f) {}
};

struct EdmondsKarp {
    int n, m;
    vector<Edge> edges;    // 边数的两倍
    vector<int> G[maxn];   // 邻接表，G[i][j]表示结点i的第j条边在e数组中的序号
    int a[maxn];           // 当起点到i的可改进量
    int p[maxn];           // 最短路树上p的入弧编号

    void init(int n) {
        for(int i = 0; i < n; i++) G[i].clear();
        edges.clear();
    }

    void AddEdge(int from, int to, int cap) {
        edges.push_back(Edge(from, to, cap, 0));
        edges.push_back(Edge(to, from, 0, 0));
        m = edges.size();
        G[from].push_back(m-2);
        G[to].push_back(m-1);
    }

    int Maxflow(int s, int t) {
        int flow = 0;
        for(;;) {
            memset(a, 0, sizeof(a));
            queue<int> Q;
            Q.push(s);
            a[s] = INF;
            while(!Q.empty()) {
                int x = Q.front(); Q.pop();
                for(int i = 0; i < G[x].size(); i++) {
                    Edge& e = edges[G[x][i]];
                    if(!a[e.to] && e.cap > e.flow) {
                        p[e.to] = G[x][i];
                        a[e.to] = min(a[x], e.cap-e.flow);
                        Q.push(e.to);
                    }
                }
                if(a[t]) break;
            }
            if(!a[t]) break;
            for(int u = t; u != s; u = edges[p[u]].from) {
                edges[p[u]].flow += a[t];
                edges[p[u]^1].flow -= a[t];
            }
            flow += a[t];
        }
        return flow;
    }
};

EdmondsKarp g;
int no[maxn][maxn];

int main() {
    int T, R, C, v, kase = 0;
    scanf("%d", &T);
    for(int kase = 1; kase <= T; kase++) {
        scanf("%d%d", &R, &C);
        g.init(R+C+2);
        int last = 0;
        for(int i = 1; i <= R; i++) {
            scanf("%d", &v);
            g.AddEdge(0, i, v - last - C); // row sum is v - last
            last = v;
        }
        last = 0;
        for(int i = 1; i <= C; i++) {
            scanf("%d", &v);
            g.AddEdge(R+i, R+C+1, v - last - R); // col sum is v - last
            last = v;
        }
        for(int i = 1; i <= R; i++)
            for(int j = 1; j <= C; j++) {
                g.AddEdge(i, R+j, 19);
                no[i][j] = g.edges.size() - 2; // no[i][j] is the index of arc for cell(i,j)
            }
        g.Maxflow(0, R+C+1);

        printf("Matrix %d\n", kase);
        for(int i = 1; i <= R; i++) {
            for(int j = 1; j <= C; j++)
                printf("%d ", g.edges[no[i][j]].flow + 1); // we subtracted 1 from every cell
            printf("\n");
        }
        printf("\n");
    }
    return 0;
}

11-9 UVa1658 Admiral ch11/UVa1658.cpp @

// UVa1658 Admiral
// Rujia Liu
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
#include<algorithm>
#include<cassert>
using namespace std;

const int maxn = 2000 + 10;
const int INF = 1000000000;

struct Edge {
    int from, to, cap, flow, cost;
    Edge(int u, int v, int c, int f, int w):from(u),to(v),cap(c),flow(f),cost(w) {}
};

struct MCMF {
    int n, m;
    vector<Edge> edges;
    vector<int> G[maxn];
    int inq[maxn];         // 是否在队列中
    int d[maxn];           // Bellman-Ford
    int p[maxn];           // 上一条弧
    int a[maxn];           // 可改进量

    void init(int n) {
        this->n = n;
        for(int i = 0; i < n; i++) G[i].clear();
        edges.clear();
    }

    void AddEdge(int from, int to, int cap, int cost) {
        edges.push_back(Edge(from, to, cap, 0, cost));
        edges.push_back(Edge(to, from, 0, 0, -cost));
        m = edges.size();
        G[from].push_back(m-2);
        G[to].push_back(m-1);
    }

    bool BellmanFord(int s, int t, int flow_limit, int& flow, int& cost) {
        for(int i = 0; i < n; i++) d[i] = INF;
        memset(inq, 0, sizeof(inq));
        d[s] = 0; inq[s] = 1; p[s] = 0; a[s] = INF;

        queue<int> Q;
        Q.push(s);
        while(!Q.empty()) {
            int u = Q.front(); Q.pop();
            inq[u] = 0;
            for(int i = 0; i < G[u].size(); i++) {
                Edge& e = edges[G[u][i]];
                if(e.cap > e.flow && d[e.to] > d[u] + e.cost) {
                    d[e.to] = d[u] + e.cost;
                    p[e.to] = G[u][i];
                    a[e.to] = min(a[u], e.cap - e.flow);
                    if(!inq[e.to]) { Q.push(e.to); inq[e.to] = 1; }
                }
            }
        }
        if(d[t] == INF) return false;
        if(flow + a[t] > flow_limit) a[t] = flow_limit - flow;
        flow += a[t];
        cost += d[t] * a[t];
        for(int u = t; u != s; u = edges[p[u]].from) {
            edges[p[u]].flow += a[t];
            edges[p[u]^1].flow -= a[t];
        }
        return true;
    }

    // 需要保证初始网络中没有负权圈
    int MincostFlow(int s, int t, int flow_limit, int& cost) {
        int flow = 0; cost = 0;
        while(flow < flow_limit && BellmanFord(s, t, flow_limit, flow, cost));
        return flow;
    }

};

MCMF g;

int main() {
    int n, m, a, b, c;
    while(scanf("%d%d", &n, &m) == 2 && n) {
        g.init(n*2-2);

        // 点2~n-1拆成弧i->i'，前者编号为0~n-1，后者编号为n~2n-3
        for(int i = 2; i <= n-1; i++)
            g.AddEdge(i-1, i+n-2, 1, 0);

        while(m--) {
            scanf("%d%d%d", &a, &b, &c);
            // 连a'->b
            if(a != 1 && a != n) a += n-2; else a--;
            b--;
            g.AddEdge(a, b, 1, c);
        }
        int cost;
        g.MincostFlow(0, n-1, 2, cost);
        printf("%d\n", cost);
    }
    return 0;
}

11-10 UVa1349 Optimal Bus Route Design ch11/UVa1349.cpp @

// UVa1349 Optimal Bus Route Design
// Rujia Liu
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
#include<algorithm>
#include<cassert>
using namespace std;

const int maxn = 200 + 10;
const int INF = 1000000000;

struct Edge {
    int from, to, cap, flow, cost;
    Edge(int u, int v, int c, int f, int w):from(u),to(v),cap(c),flow(f),cost(w) {}
};

struct MCMF {
    int n, m;
    vector<Edge> edges;
    vector<int> G[maxn];
    int inq[maxn];         // 是否在队列中
    int d[maxn];           // Bellman-Ford
    int p[maxn];           // 上一条弧
    int a[maxn];           // 可改进量

    void init(int n) {
        this->n = n;
        for(int i = 0; i < n; i++) G[i].clear();
        edges.clear();
    }

    void AddEdge(int from, int to, int cap, int cost) {
        edges.push_back(Edge(from, to, cap, 0, cost));
        edges.push_back(Edge(to, from, 0, 0, -cost));
        m = edges.size();
        G[from].push_back(m-2);
        G[to].push_back(m-1);
    }

    bool BellmanFord(int s, int t, int& flow, int& cost) {
        for(int i = 0; i < n; i++) d[i] = INF;
        memset(inq, 0, sizeof(inq));
        d[s] = 0; inq[s] = 1; p[s] = 0; a[s] = INF;

        queue<int> Q;
        Q.push(s);
        while(!Q.empty()) {
            int u = Q.front(); Q.pop();
            inq[u] = 0;
            for(int i = 0; i < G[u].size(); i++) {
                Edge& e = edges[G[u][i]];
                if(e.cap > e.flow && d[e.to] > d[u] + e.cost) {
                    d[e.to] = d[u] + e.cost;
                    p[e.to] = G[u][i];
                    a[e.to] = min(a[u], e.cap - e.flow);
                    if(!inq[e.to]) { Q.push(e.to); inq[e.to] = 1; }
                }
            }
        }
        if(d[t] == INF) return false;
        flow += a[t];
        cost += d[t] * a[t];
        for(int u = t; u != s; u = edges[p[u]].from) {
            edges[p[u]].flow += a[t];
            edges[p[u]^1].flow -= a[t];
        }
        return true;
    }

    // 需要保证初始网络中没有负权圈
    int MincostMaxflow(int s, int t, int& cost) {
        int flow = 0; cost = 0;
        while(BellmanFord(s, t, flow, cost));
        return flow;
    }

};

MCMF g;

int main() {
    int n, m, d, k;
    while(scanf("%d", &n) == 1 && n) {
        g.init(n*2+2);
        for(int u = 1; u <= n; u++) {
            g.AddEdge(0, u, 1, 0);
            g.AddEdge(n+u, n*2+1, 1, 0);
        }
        for(int i = 1; i <= n; i++) {
            for(;;) {
                int j;
                scanf("%d", &j); if(j == 0) break;
                scanf("%d", &d);
                g.AddEdge(i, j+n, 1, d);
            }
        }

        int cost;
        int flow = g.MincostMaxflow(0, n*2+1, cost);
        if(flow < n) printf("N\n");
        else printf("%d\n", cost);
    }
    return 0;
}

11-11 UVa12661 Funny Car Racing @
```
nill
```

11-12 UVa1515 Pool construction ch11/UVa1515.cpp @

// UVa1515 Pool Construction
// Rujia Liu
// 因为图较大，所以采用Dinic而不是EdmondsKarp
// 得益于接口一致性，读者无须理解Dinic就能使用它。
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
using namespace std;

const int maxn = 50*50+10;

const int INF = 1000000000;

struct Edge {
    int from, to, cap, flow;
};

bool operator < (const Edge& a, const Edge& b) {
    return a.from < b.from || (a.from == b.from && a.to < b.to);
}

struct Dinic {
    int n, m, s, t;
    vector<Edge> edges;    // 边数的两倍
    vector<int> G[maxn];   // 邻接表，G[i][j]表示结点i的第j条边在e数组中的序号
    bool vis[maxn];        // BFS使用
    int d[maxn];           // 从起点到i的距离
    int cur[maxn];         // 当前弧指针

    void init(int n) {
        for(int i = 0; i < n; i++) G[i].clear();
        edges.clear();
    }

    void AddEdge(int from, int to, int cap) {
        edges.push_back((Edge){from, to, cap, 0});
        edges.push_back((Edge){to, from, 0, 0});
        m = edges.size();
        G[from].push_back(m-2);
        G[to].push_back(m-1);
    }

    bool BFS() {
        memset(vis, 0, sizeof(vis));
        queue<int> Q;
        Q.push(s);
        vis[s] = 1;
        d[s] = 0;
        while(!Q.empty()) {
            int x = Q.front(); Q.pop();
            for(int i = 0; i < G[x].size(); i++) {
                Edge& e = edges[G[x][i]];
                if(!vis[e.to] && e.cap > e.flow) {
                    vis[e.to] = 1;
                    d[e.to] = d[x] + 1;
                    Q.push(e.to);
                }
            }
        }
        return vis[t];
    }

    int DFS(int x, int a) {
        if(x == t || a == 0) return a;
        int flow = 0, f;
        for(int& i = cur[x]; i < G[x].size(); i++) {
            Edge& e = edges[G[x][i]];
            if(d[x] + 1 == d[e.to] && (f = DFS(e.to, min(a, e.cap-e.flow))) > 0) {
                e.flow += f;
                edges[G[x][i]^1].flow -= f;
                flow += f;
                a -= f;
                if(a == 0) break;
            }
        }
        return flow;
    }

    int Maxflow(int s, int t) {
        this->s = s; this->t = t;
        int flow = 0;
        while(BFS()) {
            memset(cur, 0, sizeof(cur));
            flow += DFS(s, INF);
        }
        return flow;
    }
};

Dinic g;

int w, h;
char pool;

inline int ID(int i, int j) { return i*w+j; }

int main() {
    int T, d, f, b;
    scanf("%d", &T);
    while(T--) {
        scanf("%d%d%d%d%d", &w, &h, &d, &f, &b);
        for(int i = 0; i < h; i++) scanf("%s", pool[i]);
        int cost = 0;
        for(int i = 0; i < h; i++) {
            if(pool[i] == '.') { pool[i] = '#'; cost += f; }
            if(pool[i][w-1] == '.') { pool[i][w-1] = '#'; cost += f; }
        }
        for(int i = 0; i < w; i++) {
            if(pool[i] == '.') { pool[i] = '#'; cost += f; }
            if(pool[h-1][i] == '.') { pool[h-1][i] = '#'; cost += f; }
        }
        g.init(h*w+2);

        for(int i = 0; i < h; i++)
            for(int j = 0; j < w; j++){
                if(pool[i][j] == '#') { // grass
                    int cap = INF;
                    if(i != 0 && i != h-1 && j != 0 && j != w-1) cap = d;
                    g.AddEdge(h*w, ID(i,j), cap); // s->grass, cap=d or inf
                } else { // hole
                    g.AddEdge(ID(i,j), h*w+1, f); // hole->t, cap=f
                }
                if(i > 0)   g.AddEdge(ID(i,j), ID(i-1,j), b);
                if(i < h-1) g.AddEdge(ID(i,j), ID(i+1,j), b);
                if(j > 0)   g.AddEdge(ID(i,j), ID(i,j-1), b);
                if(j < w-1) g.AddEdge(ID(i,j), ID(i,j+1), b);
            }
        printf("%d\n", cost + g.Maxflow(h*w, h*w+1));
    }
    return 0;
}

11-13 UVa10735 Euler Circuit ch11/UVa10735.cpp @

// UVa10735 Euler Circuit
// Rujia Liu
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
using namespace std;

const int INF = 1000000000;

struct Edge {
    int from, to, cap, flow;
    Edge(int u, int v, int c, int f):from(u),to(v),cap(c),flow(f) {}
};

const int maxn = 100+10;

struct EdmondsKarp {
    int n, m;
    vector<Edge> edges;    // 边数的两倍
    vector<int> G[maxn];   // 邻接表，G[i][j]表示结点i的第j条边在e数组中的序号
    int a[maxn];           // 当起点到i的可改进量
    int p[maxn];           // 最短路树上p的入弧编号

    void init(int n) {
        for(int i = 0; i < n; i++) G[i].clear();
        edges.clear();
    }

    void AddEdge(int from, int to, int cap) {
        edges.push_back(Edge(from, to, cap, 0));
        edges.push_back(Edge(to, from, 0, 0));
        m = edges.size();
        G[from].push_back(m-2);
        G[to].push_back(m-1);
    }

    int Maxflow(int s, int t) {
        int flow = 0;
        for(;;) {
            memset(a, 0, sizeof(a));
            queue<int> Q;
            Q.push(s);
            a[s] = INF;
            while(!Q.empty()) {
                int x = Q.front(); Q.pop();
                for(int i = 0; i < G[x].size(); i++) {
                    Edge& e = edges[G[x][i]];
                    if(!a[e.to] && e.cap > e.flow) {
                        p[e.to] = G[x][i];
                        a[e.to] = min(a[x], e.cap-e.flow);
                        Q.push(e.to);
                    }
                }
                if(a[t]) break;
            }
            if(!a[t]) break;
            for(int u = t; u != s; u = edges[p[u]].from) {
                edges[p[u]].flow += a[t];
                edges[p[u]^1].flow -= a[t];
            }
            flow += a[t];
        }
        return flow;
    }
};

EdmondsKarp g;

const int maxm = 500 + 5;

int n, m, u[maxm], v[maxm], directed[maxm], id[maxm], diff[maxn];

// for euler tour only
vector<int> G[maxn];
vector<int> vis[maxn];
vector<int> path;

void euler(int u) {
    for(int i = 0; i < G[u].size(); i++)
        if(!vis[u][i]) {
            vis[u][i] = 1;
            euler(G[u][i]);
            path.push_back(G[u][i]+1);
        }
}

void print_answer() {
    // build the new graph
    for(int i = 0; i < n; i++) { G[i].clear(); vis[i].clear(); }
    for(int i = 0; i < m; i++) {
        bool rev = false;
        if(!directed[i] && g.edges[id[i]].flow > 0) rev = true;
        if(!rev) { G[u[i]].push_back(v[i]); vis[u[i]].push_back(0); }
        else { G[v[i]].push_back(u[i]); vis[v[i]].push_back(0); }
    }

    // print euler tour
    path.clear();
    euler(0);

    printf("1");
    for(int i = path.size()-1; i >= 0; i--) printf(" %d", path[i]);
    printf("\n");
}

int main() {
    int T;
    scanf("%d", &T);

    while(T--) {
        scanf("%d%d", &n, &m);
        g.init(n+2);

        memset(diff, 0, sizeof(diff));
        for(int i = 0; i < m; i++) {
            char dir;
            scanf("%d%d%s", &u[i], &v[i], dir);
            u[i]--; v[i]--;
            directed[i] = (dir == 'D' ? 1 : 0);
            diff[u[i]]++; diff[v[i]]--;
            if(!directed[i]) { id[i] = g.edges.size(); g.AddEdge(u[i], v[i], 1); }
        }

        bool ok = true;
        for(int i = 0; i < n; i++)
            if(diff[i] % 2 != 0) { ok = false; break; }

        int s = n, t = n+1;
        if(ok) {
            int sum = 0;
            for(int i = 0; i < n; i++) {
                if(diff[i] > 0) { g.AddEdge(s, i, diff[i]/2); sum += diff[i]/2; } // provide "out-degree"
                if(diff[i] < 0) { g.AddEdge(i, t, -diff[i]/2); }
            }
            if(g.Maxflow(s, t) != sum) ok = false;
        }

        if(!ok) printf("No euler circuit exist\n");
        else print_answer(); // underlying graph is always connected

        if(T) printf("\n");
    }
    return 0;
}

11-14 UVa1279 Asteroid Rangers ch11/UVa1279.cpp @

// UVa1279 Asteroid Rangers
// Rujia Liu
#include<cstdio>
#include<cmath>
#include<vector>
#include<algorithm>
using namespace std;

const int maxn = 50 + 5;
const int maxks = maxn * (maxn+1) / 2;
const double eps = 1e-8;

int n, nks;

// event
struct Event {
    double t;
    int newks, oldks; // After event, newks will be smaller than oldks
    Event(double t=0, int newks=0, int oldks=0) : t(t), newks(newks), oldks(oldks) {}
    bool operator < (const Event& rhs) const {
        return t - rhs.t < 0;
    }
};
vector <Event> events;

struct KineticPoint {
    double x, y, z; // initial position
    double dx, dy, dz; // velocity
    void read() {
        scanf("%lf%lf%lf%lf%lf%lf", &x, &y, &z, &dx, &dy, &dz);
    }
} kp[maxn];

struct KineticSegment {
    double a, b, c; // length is at^2+bt+c
    int u, v; // end point IDs
    bool operator < (const KineticSegment& rhs) const { // compare initial length
        return c - rhs.c < 0;
    }
} ks[maxks];

inline double sqr(double x) { return x * x; }

// union-find
int pa[maxn];

void init_ufset() { for(int i = 0; i < n; i++) pa[i] = i; }
int findset(int x) { return pa[x] != x ? pa[x] = findset(pa[x]) : x; }

void make_segments() {
    nks = 0;
    for(int i = 0; i < n; i++)
        for(int j = i+1; j < n; j++) {
            // the square distance between point i and point j is sum{((kp[i].dx-kp[j].dx) * t + (kp[i].x-kp[j].x))^2}
            // which can be re-written to at^2+bt+c. a>0, c>0
            ks[nks].a = sqr(kp[i].dx-kp[j].dx) + sqr(kp[i].dy-kp[j].dy) + sqr(kp[i].dz-kp[j].dz);
            ks[nks].b = 2*((kp[i].dx-kp[j].dx)*(kp[i].x-kp[j].x) + (kp[i].dy-kp[j].dy)*(kp[i].y-kp[j].y) + (kp[i].dz-kp[j].dz)*(kp[i].z-kp[j].z));
            ks[nks].c = sqr(kp[i].x-kp[j].x) + sqr(kp[i].y-kp[j].y) + sqr(kp[i].z-kp[j].z);
            ks[nks].u = i;
            ks[nks].v = j;
            nks++;
        }
    sort(ks, ks + nks);
}

void make_events() {
    events.clear();
    for(int i = 0; i < nks; i++)
        for(int j = i+1; j < nks; j++) {
            // when segment i's length is equal to segment j?
            int s1 = i, s2 = j;
            if (ks[s1].a - ks[s2].a < 0) s1 = j, s2 = i; // s1 is more steep (bigger a value)

            double a = ks[s1].a - ks[s2].a;
            double b = ks[s1].b - ks[s2].b;
            double c = ks[s1].c - ks[s2].c;
            if(fabs(a) < eps) { // bt + c = 0
                if (fabs(b) < eps) continue; // no solution
                if (b > 0) { swap(s1, s2); b = -b; c = -c; } // bt + c = 0, b < 0
                if (c > 0) events.push_back(Event(-c / b, s1, s2)); // t > 0
                continue;
            }
            double delta = b * b - 4 * a * c;
            if (delta < eps) continue; // no solution
            delta = sqrt(delta);
            double t1 = -(b + delta) / (2 * a); // solution 1
            double t2 = (delta - b) / (2 * a); // solution 2
            if (t1 > 0) events.push_back(Event(t1, s1, s2)); // steep one will be smaller
            if (t2 > 0) events.push_back(Event(t2, s2, s1)); // flat one will be smaller
        }
    sort(events.begin(), events.end());
}

int solve() {
    int pos[maxks]; // pos[i] is the index of i-th segment in the MST. 0 means "not in MST"
    int e[maxn];    // e[i] (i > 0) is the i-th edge in current MST. pos[e[i]] = i

    // initial MST
    init_ufset();
    for(int i = 0; i < nks; i++) pos[i] = 0;
    int idx = 0;
    for(int i = 0; i < nks; i++) {
        int u = findset(ks[i].u), v = findset(ks[i].v);
        if (u != v) {
            e[pos[i] = ++idx] = i;
            pa[u] = v;
        }
        if(idx == n-1) break;
    }

    int ans = 1;
    for(int i = 0; i < events.size(); i++) {
        if(pos[events[i].oldks] && (!pos[events[i].newks])) {
            init_ufset();
            int oldpos = pos[events[i].oldks];
            for(int j = 1; j < n; j++)
                if (j != oldpos) {
                    int u = findset(ks[e[j]].u), v = findset(ks[e[j]].v);
                    if(u != v) pa[u] = v;
                }
            int u = findset(ks[events[i].newks].u), v = findset(ks[events[i].newks].v);
            if(u != v) {
                // new MST found! now replace oldks with newks
                ans++;
                pos[events[i].newks] = oldpos;
                e[oldpos] = events[i].newks;
                pos[events[i].oldks] = 0;
            }
        }
    }
    return ans;
}

int main() {
    int kase = 0;
    while(scanf("%d", &n) == 1) {
        for(int i = 0; i < n; i++) kp[i].read();
        make_segments();
        make_events();
        int ans = solve();
        printf("Case %d: %d\n", ++kase, ans);
    }
    return 0;
}

11-15 UVa1659 Help Little Laura ch11/UVa1659.cpp @

// UVa1659 Help Little Laura
// Rujia Liu
// 算法一：改造网络，去掉负权
#include<cstdio>
#include<cmath>
#include<cstring>
#include<queue>
#include<vector>
#include<algorithm>
#include<cassert>
using namespace std;

const int maxn = 100 + 10;
const int INF = 1000000000;

struct Edge {
    int from, to, cap, flow;
    double cost;
    Edge(int u, int v, int c, int f, double w):from(u),to(v),cap(c),flow(f),cost(w) {}
};

struct MCMF {
    int n, m;
    vector<Edge> edges;
    vector<int> G[maxn];
    int inq[maxn];         // 是否在队列中
    double d[maxn];        // Bellman-Ford
    int p[maxn];           // 上一条弧
    int a[maxn];           // 可改进量

    void init(int n) {
        this->n = n;
        for(int i = 0; i < n; i++) G[i].clear();
        edges.clear();
    }

    void AddEdge(int from, int to, int cap, double cost) {
        edges.push_back(Edge(from, to, cap, 0, cost));
        edges.push_back(Edge(to, from, 0, 0, -cost));
        m = edges.size();
        G[from].push_back(m-2);
        G[to].push_back(m-1);
    }

    bool BellmanFord(int s, int t, int& flow, double& cost) {
        for(int i = 0; i < n; i++) d[i] = INF;
        memset(inq, 0, sizeof(inq));
        d[s] = 0; inq[s] = 1; p[s] = 0; a[s] = INF;

        queue<int> Q;
        Q.push(s);
        while(!Q.empty()) {
            int u = Q.front(); Q.pop();
            inq[u] = 0;
            for(int i = 0; i < G[u].size(); i++) {
                Edge& e = edges[G[u][i]];
                if(e.cap > e.flow && d[e.to] > d[u] + e.cost) {
                    d[e.to] = d[u] + e.cost;
                    p[e.to] = G[u][i];
                    a[e.to] = min(a[u], e.cap - e.flow);
                    if(!inq[e.to]) { Q.push(e.to); inq[e.to] = 1; }
                }
            }
        }
        if(d[t] == INF) return false;
        flow += a[t];
        cost += d[t] * a[t];
        for(int u = t; u != s; u = edges[p[u]].from) {
            edges[p[u]].flow += a[t];
            edges[p[u]^1].flow -= a[t];
        }
        return true;
    }

    // 需要保证初始网络中没有负权圈
    int MincostMaxflow(int s, int t, double& cost) {
        int flow = 0; cost = 0;
        while(BellmanFord(s, t, flow, cost));
        return flow;
    }

};

MCMF g;

int x[maxn], y[maxn], c1[maxn], c2[maxn];
vector<int> G[maxn];

int main() {
    int n, a, b, v, kase = 0;
    while(scanf("%d%d%d", &n, &a, &b) == 3) {
        g.init(n+2);
        for(int u = 0; u < n; u++) {
            scanf("%d%d", &x[u], &y[u]);
            G[u].clear();
            for(;;) {
                scanf("%d", &v);
                if(v == 0) break;
                G[u].push_back(v-1);
            }
        }

        memset(c1, 0, sizeof(c1));
        memset(c2, 0, sizeof(c2));
        double sum = 0;
        for(int u = 0; u < n; u++) {
            for(int i = 0; i < G[u].size(); i++) {
                int v = G[u][i];
                double d = sqrt((x[u] - x[v])*(x[u] - x[v]) + (y[u] - y[v])*(y[u] - y[v]));
                double edge_cost = -d*a+b; // minimize sum{edge_cost}
            if(edge_cost >= 0) {
                g.AddEdge(u, v, 1, edge_cost);
            } else {
                g.AddEdge(v, u, 1, -edge_cost);
                c1[v]++; c2[u]++;
                sum += -edge_cost;
            }
            }
        }
        for(int u = 0; u < n; u++) {
            if(c1[u] > c2[u]) g.AddEdge(n, u, c1[u]-c2[u], 0);
            if(c2[u] > c1[u]) g.AddEdge(u, n+1, c2[u]-c1[u], 0);
        }

        double cost;
        int flow = g.MincostMaxflow(n, n+1, cost);
        double ans = sum - cost;
        if(ans < 0) ans = 0; // avoid -0.0
        printf("Case %d: %.2lf\n", ++kase, ans);
    }
    return 0;
}

12-1 UVa1671 History of Languages ch12/UVa1671.cpp @

// UVa1671 History of Languages
// Rujia Liu
//
// This is Problem 12-1 of <<Beginning Algorithm Contests>> 2nd edition
//
// We want to test whether A intersects with ~B (finalA = 1, finalB = 0), or B intersects with ~A (finalA = 0, finalB = 1)
// So we can do a single DFS instead of two, checking finalA XOR finals B=1
#include<cstdio>
#include<cstring>
using namespace std;

const int maxn = 2000 + 5;
const int maxt = 26;

// Note: state 0 is a dummy state, other states' number is increased by 1
struct DFA {
    int n;
    int is_final[maxn];
    int next[maxn][maxt];
    void read(int t) {
        scanf("%d", &n);
        for(int i = 1; i <= n; i++) {
            scanf("%d", &is_final[i]);
            for(int c = 0; c < t; c++) {
                int s;
                scanf("%d", &s);
                next[i][c] = s+1;
            }
        }
        is_final = 0; // dummy state is not final
    }
}A, B;

int vis[maxn][maxn], kase, t;

// try to find a common string starting from (s1, s2)
bool dfs(int s1, int s2) {
    vis[s1][s2] = kase;
    if(A.is_final[s1] ^ B.is_final[s2]) return true;
    for(int i = 0; i < t; i++) {
        int nexta = A.next[s1][i];
        int nextb = B.next[s2][i];
        if(vis[nexta][nextb] != kase && dfs(nexta, nextb)) return true;
    }
    return false;
}

int main() {
    kase = 0;
    memset(vis, 0, sizeof(vis));
    while(scanf("%d", &t) == 1 && t) {
        A.read(t);
        B.read(t);
        printf("Case #%d: ", ++kase);
        if(dfs(1, 1)) printf("No\n");
        else printf("Yes\n");
    }
    return 0;
}

12-2 UVa1672 Disjoint Regular Expressions ch12/uva1672.cpp @

// UVa1672 Disjoint Regular Expressions
// Rujia Liu
//
// This is Problem 12-2 of <<Beginning Algorithm Contests>> 2nd edition
//
// This code is neither simplest nor most efficient, but it's easy to understand and fast enough.
// Algorithm implemented here:
//   1. build epsilon-NFA from the regex
//   2. build NFA by removing epsilon from epsilon-NFA. Note that we did NOT optimize the epsilon-NFA as described in the book.
//   3. use BFS to find a common string of these two NFAs
// Attention: the output should NOT be empty so we used a little trick.
//
// Alternative algorithm: do BFS directly on epsilon-NFAs.
// State is (s1,s2,b) where b=1 iff at least one non-epsilon transition is performed.
// However, this graph is now 0-1 weighted so we need to use deque (or two-phase BFS).
#include<cstdio>
#include<cstring>
#include<vector>
#include<set>
#include<string>
#include<queue>
#include<cassert>
#define REP(i,n) for(int i = 0; i < (n); ++i)

using namespace std;

// Part I: Expression Parser
struct ExprNode {
    enum {A, STAR, OR, CONCAT};
    int type, val;
    ExprNode *l, *r;

    ExprNode(int type, ExprNode* l, ExprNode* r, int val = -1):type(type),l(l),r(r),val(val){}
    ~ExprNode() {
        if(l) delete l;
        if(r) delete r;
    }
};

struct Parser {
    char* s;
    int p, n;

    void Skip(char c) { p++; } // for debug purpose

    // (u)*
    ExprNode* Item() {
        ExprNode* u;
        if(s[p] == '(') { Skip('('); u = Expr(); Skip(')'); }
        else u = new ExprNode(ExprNode::A, NULL, NULL, s[p++]);
        while(s[p] == '*') {
            Skip('*');
            u = new ExprNode(ExprNode::STAR, u, NULL);
        }
        return u;
    }

    // u1u2u3...
    ExprNode* Concat() {
        ExprNode* u = Item();
        while(s[p] && s[p] != ')' && s[p] != '|')
            u = new ExprNode(ExprNode::CONCAT, u, Item());
        return u;
    }

    // u1|u2|u3
    ExprNode* Expr() {
        ExprNode* u = Concat();
        while(s[p] == '|') {
            Skip('|');
            u = new ExprNode(ExprNode::OR, u, Concat());
        }
        return u;
    }

    ExprNode* parse(char* str) {
        s = str;
        n = strlen(s);
        p = 0;
        return Expr();
    }

};

// Part II: NFA construction
const int maxs = 100 * 4 + 5;

struct NFA {
    int n; // number of states

    struct Transition {
        int ch, next;
        Transition(int ch = 0, int next = 0):ch(ch),next(next){}
        bool operator < (const Transition& rhs) const {
            if(ch != rhs.ch) return ch < rhs.ch;
            return next < rhs.next;
        }
    };
    vector<Transition> trans[maxs];

    void add(int s, int t, int c) {
        trans[s].push_back(Transition(c, t));
    }

    void process(ExprNode* u) {
        int st = n++; // state 'start'
        if(u->type == ExprNode::A) add(st, n, u->val);
        else if(u->type == ExprNode::STAR) {
            process(u->l);
            add(st, st+1, -1);
            add(st, n, -1);
            add(n-1, st, -1);
        }
        else if(u->type == ExprNode::OR) {
            process(u->l);
            int m = n;
            process(u->r);
            add(st, st+1, -1);
            add(st, m, -1);
            add(m-1, n, -1);
            add(n-1, n, -1);
        }
        else if(u->type == ExprNode::CONCAT) {
            add(st, st+1, -1);
            process(u->l);
            add(n-1, n, -1);
            process(u->r);
            add(n-1, n, -1);
        }
        n++; // state 'end'
    }

    void init(char* s) {
        Parser p;
        ExprNode* root = p.parse(s);
        n = 0;
        for(int i = 0; i < maxs; i++) {
            trans[i].clear();
        }
        process(root);
        delete root;
    }

    vector<int> ss; // starting states

    void remove_epsilon() {
        // find epsilon-closure for each state
        vector<int> reachable[maxs];
        int vis[maxs];
        for(int i = 0; i < n; i++) {
            reachable[i].clear();
            reachable[i].push_back(i);
            queue<int> q;
            q.push(i);
            memset(vis, 0, sizeof(vis));
            vis[i] = 1;
            while(!q.empty()) {
                int s = q.front(); q.pop();
                for(int j = 0; j < trans[s].size(); j++)
                    if(trans[s][j].ch == -1) {
                        int s2 = trans[s][j].next;
                        if(!vis[s2]) {
                            reachable[i].push_back(s2);
                            vis[s2] = 1;
                            q.push(s2);
                        }
                    }
            }
        }
        ss = reachable;

        // merge transitions
        for(int i = 0; i < n; i++) {
            set<Transition> tr;
            for(int j = 0; j < trans[i].size(); j++) {
                if(trans[i][j].ch == -1) continue;
                int s = trans[i][j].next;
                for(int k = 0; k < reachable[s].size(); k++)
                    tr.insert(Transition(trans[i][j].ch, reachable[s][k]));
            }
            trans[i] = vector<Transition>(tr.begin(), tr.end());
        }
    }
};

// Part III: BFS to find the answer

const int maxn = 100 + 5;
const int maxq = 100 * 4 * 100 * 4 * 2 + 5; // case 26
char sa[maxn], sb[maxn];

struct State {
    int s1, s2, fa, ch;
} states[maxq];
int ns;

void print_solution(int s) {
    if(states[s].fa == -1) return;
    print_solution(states[s].fa);
    printf("%c", states[s].ch);
}

void solve(const NFA& A, const NFA& B) {
    queue<int> q;
    int vis[maxs][maxs];
    memset(vis, 0, sizeof(vis));
    ns = 0;
    REP(i, A.ss.size())
        REP(j, B.ss.size()) {
            int s1 = A.ss[i], s2 = B.ss[j];
            states[ns].s1 = s1;
            states[ns].s2 = s2;
            states[ns].fa = -1;
            q.push(ns++);
        }

    while(!q.empty()) {
        int s = q.front(); q.pop();
        int s1 = states[s].s1;
        int s2 = states[s].s2;
        if(s1 == A.n-1 && s2 == B.n-1 && states[s].fa != -1) {
            printf("Wrong\n");
            print_solution(s);
            printf("\n");
            return;
        }
        int n1 = A.trans[s1].size();
        int n2 = B.trans[s2].size();

        REP(i, n1) REP(j, n2)
            if(A.trans[s1][i].ch == B.trans[s2][j].ch) {
                int s1b = A.trans[s1][i].next;
                int s2b = B.trans[s2][j].next;
                int c = A.trans[s1][i].ch;
                if(vis[s1b][s2b]) continue;
                vis[s1b][s2b] = 1;
                states[ns].s1 = s1b;
                states[ns].s2 = s2b;
                states[ns].fa = s;
                states[ns].ch = c;
                q.push(ns++);
            }
    }
    printf("Correct\n");
}

NFA A, B;
int main() {
    while(scanf("%s%s", sa, sb) == 2) {
        A.init(sa);
        B.init(sb);
        A.remove_epsilon();
        B.remove_epsilon();
        solve(A, B);
    }
    return 0;
}

12-3 UVa1673 str2int ch12/UVa1673.cpp @

// UVa1673 str2int
// Rujia Liu
//
// This is Problem 12-3 of <<Beginning Algorithm Contests>> 2nd edition
//
// Note that we're using the "big string method", as explained in the book.
// It's slightly less efficient than the official "multiple string DAWG" because we need to explicitly store '$' edges.
// However, it's conceptually cleaner, and easier to understand.
#include <cstdio>
#include <cstring>
using namespace std;

const int maxc = 11; // 10 digits and '$'
const int maxn = 100000 + 10;

struct DAWG {
    struct Node {
        Node *fa, *next[maxc];
        int len;
        int id, pos;
        Node(){}
        Node(int len):fa(0),len(len){
            memset(next, 0, sizeof(next));
        }
    };

    Node node[maxn*2], *root, *last;
    int tot;

    Node *newnode(const Node& u) {
        node[tot] = u;
        node[tot].id = tot;
        return &node[tot++];
    }
    Node* newnode(int len) { return newnode(Node(len)); }
    Node* newnode(Node *p) { return newnode(*p); }

    void init() {
        tot = 0;
        root = last = newnode(0);
        node.pos = 0;
    }

    void add(int x,int len) {
        Node *p = last, *np = newnode(p->len + 1);
        np->pos = len;
        last = np;
        for(; p && !p->next[x];p = p->fa)
            p->next[x] = np;
        if(!p) { np->fa = root; return; }

        Node *q = p->next[x];
        if(q->len == p->len + 1) { np->fa = q; return; }

        Node *nq = newnode(q);
        nq->len = p->len + 1;
        q->fa = nq;
        np->fa = nq;
        for(; p && p->next[x] == q; p = p->fa)
            p->next[x] = nq;
    }
};


/////// problem related

const int MOD = 2012;

char s[maxn];
int topo[maxn*2], topocnt[maxn*2], sum[maxn*2], cnt[maxn*2];
DAWG g;

int main() {
    int n;
    while(scanf("%d", &n) == 1) {
        g.init();
        int totlen = 0;
        for(int i = 0; i < n; i++) {
            scanf("%s", s);
            int len = strlen(s);
            if(i > 0) g.add(10, ++totlen); // $
            for(int j = 0; j < len; j++) {
                g.add(s[j] - '0', ++totlen); // regular edges
            }
        }

        // topology sort
        for(int i = 0; i <= totlen; i++)
            topocnt[i] = 0;
        for(int i = 0; i < g.tot; i++)
            topocnt[g.node[i].len]++;
        for(int i = 1; i <= totlen; i++)
            topocnt[i] += topocnt[i-1];
        for(int i = 0; i < g.tot; i++)
            topo[--topocnt[g.node[i].len]] = i;

        int ans = 0;
        for(int i = 0; i < g.tot; i++)
            cnt[i] = sum[i] = 0;
        cnt = 1;
        for(int i = 0; i < g.tot; i++) {
            int fa = topo[i];
            DAWG::Node* u = &g.node[fa];
            for(int j = 0; j < 10; j++) {
                if(i == 0 && j == 0) continue;
                if(u->next[j]) {
                    int son = u->next[j]->id;
                    cnt[son] = (cnt[son] + cnt[fa]) % MOD;
                    sum[son] = (sum[son] + sum[fa]*10 + cnt[fa]*j) % MOD;
                }
            }
            ans = (ans + sum[fa]) % MOD;
        }
        printf("%d\n", ans);
    }
    return 0;
}

12-7 UVa12538 Version Controlled IDE ch12/UVa12538_rope.cpp @

// UVa12538 Version Controlled IDE
// Rujia Liu
// This code makes use of rope, a persistent string available in gcc's STL extensions.
#include<cstdio>
#include<iostream>
#include<ext/rope>
using namespace std;
using namespace __gnu_cxx;

const int maxn = 50000 + 5;
const int maxlen = 100000 + 5;

crope cur, versions[maxn];
char s[maxlen];

int main() {
    int n;
    scanf("%d", &n); // a single test case
    int d = 0;
    int vnow = 0;
    while(n--) {
        int op, p, c, v;
        scanf("%d", &op);
        if(op == 1) {
            scanf("%d%s", &p, s);
            p -= d;
            cur.insert(p, s);
            versions[++vnow] = cur;
        }
        else if(op == 2) {
            scanf("%d%d", &p, &c);
            p -= d; c -= d;
            cur.erase(p-1, c);
            versions[++vnow] = cur;
        }
        else {
            scanf("%d%d%d", &v, &p, &c);
            p -= d; v -= d; c -= d;
            crope r = versions[v].substr(p-1, c);
            d += count(r.begin(), r.end(), 'c');
            cout << r << "\n";
        }
    }
    return 0;
}

✂️ Bonus Problems @

Bresenham’s line algorithm - Wikipedia, the free encyclopedia @

Bresenham’s line algorithm is named after Jack Elton Bresenham who developed it in 1962 at IBM.

\[{\frac {y-y_{0}}{y_{1}-y_{0}}}={\frac {x-x_{0}}{x_{1}-x_{0}}}.\]

function line(x0, y0, x1, y1)
    real deltax := x1 - x0
    real deltay := y1 - y0
    real error := -1.0
    real deltaerr := abs(deltay / deltax)       // Assume deltax != 0 (line is not vertical),
                                                // note that this division needs to be done in a way that preserves the fractional part
    int y := y0
    for x from x0 to x1-1
        plot(x,y)
        error := error + deltaerr
        if error ≥ 0.0 then
            y := y + 1
            error := error - 1.0

+----------+                            +--------------+
| y = f(x) |                            | f(x, y) = 0  |
+----------+                            +--------------+
                                                                    A = dy
y       = f(x) = mx + b                                             B = dx
        = (dy/dx)x + b                                              C = dx*b
dx*y    = dy*x + dx*b
0       = dy*x - dx*y + dx*b            f(x,y)  = 0 = Ax + By + C

+------+
| e.g. |
+------+

y = 0.5 * x +1                          f(x, y) = x - 2y + 2

starting point: f(x0, y0) = 0

(x0+1, y0), (x0+1, y0+1)  ----- mid point : D = f(x0+1, y0+0.5)
                                            D < 0   --->    go right
                                            D > 0   --->    go down

if D is positive, then choose ( x 0 + 1 , y 0 + 1 ), otherwise choose ( x 0 + 1 , y 0 ).

Alternatively, the difference between points can be used instead of evaluating f(x,y) at midpoints. This alternative method allows for integer-only arithmetic, which is generally faster than using floating-point arithmetic. To derive the alternative method, define the difference to be as follows:

D = f(x0+1, y0+0.5) - f(x0, y0) = A(x0+1-x0) + B(y0+0.5-y0)
  = A + 0.5*B
           if    <   0 ---------->  (x0, y0)
           if    >   0 ---------->  (x0, y0+1)

plotLine(x0,y0, x1,y1)
    dx = x1 - x0
    dy = y1 - y0
    D = dy - dx
    y = y0

    for x from x0 to x1-1
        plot(x,y)
        if D ≥ 0
            y = y + 1
            D = D - dx
        D = D + dy

However, as mentioned above this is only for the first octant. This means there are eight possible cases to consider. The simplest way to extend the same algorithm, if implemented in hardware, is to flip the co-ordinate system on the input and output of the single-octant drawer.

 Octants:
  \2|1/
  3\|/0
 ---+---
  4/|\7
  /5|6\

Octant (plane geometry) - Wikipedia, the free encyclopedia: An 8-point windrose
Orthant - Wikipedia, the free encyclopedia: In two dimensions, there are 4 orthants (called quadrants)

Rotate Image | LeetCode OJ @

复制太慢！用两次翻折，如下图：

先副对角线，在中线
1   2               4   2               3   1
  /         -->      ---        --->
3   4               3   1               4   2
(i,j)
i=[0,n-1)       P(i,j)->P(n-1-j,n-1-i)
j=[0,n-1-i)

先中线，再主对角线
1   2               3   4               3   1
 ---        -->       \         --->
3   4               1   2               4   2

看来怎么翻折都是可以得。自己随意选择把。

// Rotate Image
#define REP(i, n) for (int i = 0; i < (n); i++)

class Solution {
public:
    void rotate(vector<vector<int> > &a) {
        int n = a.size();
        REP(i, n-1)
            REP(j, n-1-i)
            swap(a[i][j], a[n-1-j][n-1-i]);
        REP(i, n/2)
            swap_ranges(a[i].begin(), a[i].end(), a[n-1-i].begin());
    }
};

Gray Code | LeetCode OJ @

The gray code is a binary numeral system where two successive values differ in only one bit.

Given a non-negative integer n representing the total number of bits in the code, print the sequence of gray code. A gray code sequence must begin with 0.

For example, given n = 2, return [0,1,3,2]. Its gray code sequence is:

自然二进制码转换为格雷码：g₀ = b₀, g_i=b_i ^ b_i-1

保留自然二进制码的最高位作为格雷码的最高位，格雷码次高位为二进制码的高位与次高位异或，其余各位与次高位的求法类似。例如，将自然二进制码 1001，转换为格雷码的过程是：保留最高位；然后将第 1 位的 1 和第 2 位的 0 异或，得到 1，作为格雷码的第 2 位；将第 2 位的 0 和第 3 位的 0 异或，得到 0，作为格雷码的第 3 位；将第 3 位的 0 和第 4 位的 1 异或，得到 1，作为格雷码的第 4 位，最终，格雷码为 1101。

格雷码有数学公式，整数 n 的格雷码是 n ^ (n/2)。

这题要求生成 n 比特的所有格雷码。

方法 1，最简单的方法，利用数学公式，对从 0..2^n-1 的所有整数，转化为格雷码。
方法 2，n 比特的格雷码，可以递归地从 n-1 比特的格雷码生成。

For a given n, a gray code sequence is not uniquely defined. 首先，格雷码不是唯一的。它是一个 sequence，有 2ⁿ 个数字。每个数字，依次，只改变一个 bit。

For example, [0,2,3,1] is also a valid gray code sequence according to the above definition.

For now, the judge is able to judge based on one instance of gray code sequence. Sorry about that.

see more at Gray code - Wikipedia, the free encyclopedia.

直接用公式：

// 时间复杂度 O(2^n)，空间复杂度 O(2^n)
#define FOR(i, a, b) for (decltype(b) i = (a); i < (b); i++)        // for,     [a, b)
#define REP(i, n) FOR(i, 0, n)                                      // repeat,  [0, n)

class Solution {
public:
    vector<int> grayCode(int n) {
        int size = 1 << n;
        vector<int> r(size);
        REP(i, size)
            r[i] = i^i>>1;      // n ^ (n/2)
        return r;
    }
};

reflect and prefix 法：TODO

The first few steps of the reflect-and-prefix method.

带 * 的是每次新加入的元素。

        n=1     n=2     n=3
   *0   0       00      000
       *1       01      001
               *11      011
               *10      010
                       *110
                       *111
                       *101
                       *100

// reflect-and-prefix method // 时间复杂度 O(2^n)，空间复杂度 O(1) class Solution { public: vector grayCode(int n) { vector result; result.reserve(1<<n); result.push_back(0); for (int i = 0; i < n; i++) { const int highest_bit = 1 << i; for (int j = result.size() - 1; j >= 0; j–) // 要反着遍历，才能对称，遍历完后，尺寸加倍 result.push_back(highest_bit | result[j]); // 把 0 调整成 1 } return result; } }; ```

Single Number | LeetCode OJ @

Given an array of integers, every element appears twice except for one. Find that single one.

偶数次异或等于 0。0 异或 x 等于 x。（这个结论太重要！）

class Solution {
public:
    int singleNumber(vector<int> &a) {
        return accumulate(a.begin(), a.end(), 0, bit_xor<int>());
    }
};

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int x = 0;
        for (auto i : nums) {
            x ^= i;
        }
        return x;
    }
};

Single Number II | LeetCode OJ ♥️ @

只有一次数只出现了一次，其余都是三次。

方法1：创建一个长度为 sizeof(int) 的数组 count[sizeof(int)]，count[i] 表示在 i 位出现的 1 的次数。如果 count[i] 是 3 的整数倍，则忽略；否则就把该位取出来组成答案。

#define FOR(i, a, b) for (decltype(b) i = (a); i < (b); i++)
#define REP(i, n) FOR(i, 0, n)
class Solution {
public:
    int singleNumber(vector<int> &a) {
        vector<int> c(32);
        for (int x: a)
            REP(j, 32)
                c[j] += x>>j & 1;
        int r = 0;
        REP(j, 32)
            r |= ( c[j]%3 & 1 ) << j;
        return r;
    }
};

方法 2：用 one 记录到当前处理的元素为止，二进制 1 出现“1 次”（mod 3 之后的1）的有哪些二进制位；用 two 记录到当前计算的变量为止，二进制 1 出现“2 次”（mod 3 之后的 2）的有哪些二进制位。当 one 和 two 中的某一位同时为 1 时表示该二进制位上 1 出现了 3 次，此时需要清零。即用二进制模拟三进制运算。最终 one 记录的是最终结果。

（难以理解……）

class Solution {
public:
    int singleNumber(vector<int> &a) {
        int one = 0, two = 0;
        for (int x: a) {
            one = (one ^ x) & ~ two;
            two = (two ^ x) & ~ one;
        }
        return one;
    }
};

[1, 3, 3, 2, 1, 3, 1]                           one = (one ^ x) & ~ two;
x           one             two                 two = (two ^ x) & ~ one;
            0000,0000       0000,0000

0000,0001   0000,0001
            &
            1111,1111

0000,0001   1111,1111       0000,0001
                            &
                            0000,0000

0000,0001   1111,1111       0000,0001
3

Shift right @

from acm-cheatsheet/Functionalities

Big Integer @

addition
subtraction
multiplication
division
power

#include<cstdio>
#include<cstring>
#include<vector>
#include<iostream>
using namespace std;

struct BigInteger {
    static const int BASE = 100000000;
    static const int WIDTH = 8;
    vector<int> s;

    BigInteger(long long num = 0) { *this = num; }          // 构造函数
    BigInteger operator = (long long num) {                 // 赋值运算符
        s.clear();
        do {
            s.push_back(num % BASE);
            num /= BASE;
        } while(num > 0);
        return *this;
    }
    BigInteger operator = (const string& str) {             // 赋值运算符
        s.clear();
        int x, len = (str.length() - 1) / WIDTH + 1;
        for(int i = 0; i < len; i++) {
            int end = str.length() - i*WIDTH;
            int start = max(0, end - WIDTH);
            sscanf(str.substr(start, end-start).c_str(), "%d", &x);
            s.push_back(x);
        }
        return *this;
    }
    BigInteger operator + (const BigInteger& b) const {
        BigInteger c;
        c.s.clear();
        for(int i = 0, g = 0; ; i++) {
            if(g == 0 && i >= s.size() && i >= b.s.size()) break;
            int x = g;
            if(i < s.size()) x += s[i];
            if(i < b.s.size()) x += b.s[i];
            c.s.push_back(x % BASE);
            g = x / BASE;
        }
        return c;
    }
};

ostream& operator << (ostream &out, const BigInteger& x) {
    out << x.s.back();
    for(int i = x.s.size()-2; i >= 0; i--) {
        char buf;
        sprintf(buf, "%08d", x.s[i]);
        for(int j = 0; j < strlen(buf); j++) out << buf[j];
    }
    return out;
}

istream& operator >> (istream &in, BigInteger& x) {
    string s;
    if(!(in >> s)) return in;
    x = s;
    return in;
}

#include<set>
#include<map>
set<BigInteger> s;
map<BigInteger, int> m;

int main() {
    BigInteger y;
    BigInteger x = y;
    BigInteger z = 123;

    BigInteger a, b;
    cin >> a >> b;
    cout << a + b << "\n";
    cout << BigInteger::BASE << "\n";
    return 0;
}

AOAPC 代码选讲 @

闰年 @

#include<stdio.h>
int main() {
    int year;
    scanf( "%d", &year );
    if( year % 4 != 0 || (year % 100 == 0 && year % 400 != 0) ) {
        printf( "no\n" );
    } else {
        printf("yes\n");
    }
    return 0;
}

6-1 UVa210 并行程序模拟，Concurrency Simulator ch6/UVa210.cpp @

模拟 n 个程序

// UVa210 Concurrency Simulator
#include <cstdio>
#include <queue>
#include <cstring>
#include <cstdlib>
#include <cctype>
using namespace std;

const int maxn = 1000;

deque<int> readyQ;
queue<int> blockQ;
int n, quantum, c, var, ip[maxn];                        // ip[pid] 是程序 pid 的当前行号。所有程序都存在 prog 数组，更类似真实的情况，代码也更短
bool locked;
char prog[maxn];

void run(int pid) {
    int q = quantum;
    while(q > 0) {
        char *p = prog[ip[pid]];
        switch(p) {
            case '=':
                var[p - 'a'] = isdigit(p) ? (p - '0') * 10 + p - '0' : p - '0';
                q -= c;
                break;
            case 'i': // print
                printf("%d: %d\n", pid+1, var[p - 'a']);
                q -= c;
                break;
            case 'c': // lock
                if(locked) { blockQ.push(pid); return; }
                locked = true;
                q -= c;
                break;
            case 'l': // unlock
                locked = false;
                if(!blockQ.empty()) {
                    int pid2 = blockQ.front(); blockQ.pop();
                    readyQ.push_front(pid2);
                }
                q -= c;
                break;
            case 'd': // end
                return;
        }
        ip[pid]++;
    }
    readyQ.push_back(pid);
}

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        scanf("%d %d %d %d %d %d %d\n", &n, &c, &c, &c, &c, &c, &quantum);
        memset(var, 0, sizeof(var));

        int line = 0;
        for(int i = 0; i < n; i++) {
            fgets(prog[line++], maxn, stdin);
            ip[i] = line - 1;
            while(prog[line - 1] != 'd')
                fgets(prog[line++], maxn, stdin);
            readyQ.push_back(i);
        }

        locked = false;
        while(!readyQ.empty()) {
            int pid = readyQ.front(); readyQ.pop_front();
            run(pid);
        }
        if(T) printf("\n");
    }
    return 0;
}

6-2 UVa514 Rails ch6/UVa514.cpp @

// UVa514 Rails
// Rujia Liu
#include<cstdio>
#include<stack>
using namespace std;
const int MAXN = 1000 + 10;

int n, target[MAXN];

int main() {
    while(scanf("%d", &n) == 1) {
        stack<int> s;
        int A = 1, B = 1;
        for(int i = 1; i <= n; i++)
            scanf("%d", &target[i]);
        int ok = 1;
        while(B <= n) {
            if(A == target[B]){ A++; B++; }
            else if(!s.empty() && s.top() == target[B]){ s.pop(); B++; }
            else if(A <= n) s.push(A++);
            else { ok = 0; break; }
        }
        printf("%s\n", ok ? "Yes" : "No");
    }
    return 0;
}

6-3 UVa442 Matrix Chain Multiplication ch6/UVa442.cpp @

// UVa442 Matrix Chain Multiplication
// Rujia Liu
// 题意：输入n个矩阵的维度和一些矩阵链乘表达式，输出乘法的次数。假定A和m*n的，B是n*p的，那么AB是m*p的，乘法次数为m*n*p
// 算法：用一个栈。遇到字母时入栈，右括号时出栈并计算，然后结果入栈。因为输入保证合法，括号无序入栈
#include<cstdio>
#include<stack>
#include<iostream>
#include<string>
using namespace std;

struct Matrix {
    int a, b;
    Matrix(int a=0, int b=0):a(a),b(b) {}
} m;

stack<Matrix> s;

int main() {
    int n;
    cin >> n;
    for(int i = 0; i < n; i++) {
        string name;
        cin >> name;
        int k = name - 'A';
        cin >> m[k].a >> m[k].b;
    }
    string expr;
    while(cin >> expr) {
        int len = expr.length();
        bool error = false;
        int ans = 0;
        for(int i = 0; i < len; i++) {
            if(isalpha(expr[i])) s.push(m[expr[i] - 'A']);
            else if(expr[i] == ')') {
                Matrix m2 = s.top(); s.pop();
                Matrix m1 = s.top(); s.pop();
                if(m1.b != m2.a) { error = true; break; }
                ans += m1.a * m1.b * m2.b;
                s.push(Matrix(m1.a, m2.b));
            }
        }
        if(error) printf("error\n"); else printf("%d\n", ans);
    }

    return 0;
}

6-4 UVa11988 Broken Keyboard @

// UVa11988 Broken Keyboard
// Rujia Liu
#include<cstdio>
#include<cstring>
const int maxn = 100000 + 5;
int last, cur, next[maxn]; // 光标位于cur号字符之后面
char s[maxn];

int main() {
    while(scanf("%s", s+1) == 1) {
        int n = strlen(s+1); // 输入保存在s, s...中
        last = cur = 0;
        next = 0;

        for(int i = 1; i <= n; i++) {
            char ch = s[i];
            if(ch == '[') cur = 0;
            else if(ch == ']') cur = last;
            else {
                next[i] = next[cur];
                next[cur] = i;
                if(cur == last) last = i; // 更新“最后一个字符”编号
                cur = i; // 移动光标
            }
        }
        for(int i = next; i != 0; i = next[i])
            printf("%c", s[i]);
        printf("\n");
    }
    return 0;
}

6-5 UVa12657 Boxes in a Line ch6/UVa12657.cpp

// UVa12657 Boxes in a Line
// Rujia Liu
#include<cstdio>
#include<algorithm>
using namespace std;

const int maxn = 100000 + 5;
int n, left[maxn], right[maxn];

inline void link(int L, int R) {
    right[L] = R; left[R] = L;
}

int main() {
    int m, kase = 0;
    while(scanf("%d%d", &n, &m) == 2) {
        for(int i = 1; i <= n; i++) {
            left[i] = i-1;
            right[i] = (i+1) % (n+1);
        }
        right = 1; left = n;
        int op, X, Y, inv = 0;

        while(m--) {
            scanf("%d", &op);
            if(op == 4) inv = !inv;
            else {
                scanf("%d%d", &X, &Y);
                if(op == 3 && right[Y] == X) swap(X, Y);
                if(op != 3 && inv) op = 3 - op;
                if(op == 1 && X == left[Y]) continue;
                if(op == 2 && X == right[Y]) continue;

                int LX = left[X], RX = right[X], LY = left[Y], RY = right[Y];
                if(op == 1) {
                    link(LX, RX); link(LY, X); link(X, Y);
                }
                else if(op == 2) {
                    link(LX, RX); link(Y, X); link(X, RY);
                }
                else if(op == 3) {
                    if(right[X] == Y) { link(LX, Y); link(Y, X); link(X, RY); }
                    else { link(LX, Y); link(Y, RX); link(LY, X); link(X, RY); }
                }
            }
        }

        int b = 0;
        long long ans = 0;
        for(int i = 1; i <= n; i++) {
            b = right[b];
            if(i % 2 == 1) ans += b;
        }
        if(inv && n % 2 == 0) ans = (long long)n*(n+1)/2 - ans;
        printf("Case %d: %lld\n", ++kase, ans);
    }
    return 0;
}

6-6 UVa679 Dropping Balls UVa679.cpp @

ch6, page148.

每个节点有一个开关，每次有小球通过，开关 toggle。初始为可以向左。

// UVa679 Dropping Balls
// Rujia Liu
#include<cstdio>
int main() {
  int T, D, I;
  scanf("%d", &T);
  while(T--) {
    scanf("%d%d", &D, &I);
    int k = 1;
    for(int i = 0; i < D-1; i++)
      if(I%2) { k = k*2; I = (I+1)/2; }
      else { k = k*2+1; I /= 2; }
    printf("%d\n", k);
  }
  return 0;
}

6-8 UVa548 Tree ch6/UVa548.cpp @

ch6, page156.

题意：给一棵点带权（权各不相同，都是正整数）二叉树的中序和后序遍历，找一个叶子使得它到根的路径上的权和最小。如果有多解，该叶子本身的权应尽量小

算法：递归建树，然后 DFS。注意，直接递归求结果也可以，但是先建树的方法不仅直观，而且更好调试

// UVa548 Tree
#include<iostream>
#include<string>
#include<sstream>
#include<algorithm>
using namespace std;

// 因为各个结点的权值各不相同且都是正整数，直接用权值作为结点编号
const int maxv = 10000 + 10;
int in_order[maxv], post_order[maxv], lch[maxv], rch[maxv];
int n;

bool read_list(int* a) {
    string line;
    if(!getline(cin, line)) return false;
    stringstream ss(line);
    n = 0;
    int x;
    while(ss >> x) a[n++] = x;
    return n > 0;
}

// 把in_order[L1..R1]和post_order[L2..R2]建成一棵二叉树，返回树根
int build(int L1, int R1, int L2, int R2) {
    if(L1 > R1) return 0; // 空树
    int root = post_order[R2];
    int p = L1;
    while(in_order[p] != root) p++;
    int cnt = p-L1; // 左子树的结点个数
    lch[root] = build(L1, p-1, L2, L2+cnt-1);
    rch[root] = build(p+1, R1, L2+cnt, R2-1);
    return root;
}

int best, best_sum; // 目前为止的最优解和对应的权和

void dfs(int u, int sum) {
    sum += u;
    if(!lch[u] && !rch[u]) { // 叶子
        if(sum < best_sum || (sum == best_sum && u < best)) { best = u; best_sum = sum; }
    }
    if(lch[u]) dfs(lch[u], sum);
    if(rch[u]) dfs(rch[u], sum);
}

int main() {
    while(read_list(in_order)) {
        read_list(post_order);
        build(0, n-1, 0, n-1);
        best_sum = 1000000000;
        dfs(post_order[n-1], 0);
        cout << best << "\n";
    }
    return 0;
}

也可以在递归的同时统计最优解。留给读者。

Falling Leaves @

// UVa699 The Falling Leaves
// Rujia Liu
// 题意：给一棵二叉树，每个节点都有一个水平位置：左儿子在它左边1个单位，右儿子在右边1个单位。从左向右输出每个水平位置的所有结点的权值之和。按照递归方式输入，-1表示空树
// 算法：在“建树”的同时计算，无须真正的把树保存下来

#include<cstring>
#include<iostream>
using namespace std;

const int maxn = 200;
int sum[maxn];

// 输入并统计一棵子树，树根水平位置为p
void build(int p) {
    int v;
    cin >> v;
    if(v == -1) return; // 空树
    sum[p] += v;
    build(p - 1);
    build(p + 1);
}

// 边读入边统计
bool init() {
    int v;
    cin >> v;
    if(v == -1) return false;

    memset(sum, 0, sizeof(sum));
    int pos = maxn/2; // 树根的水平位置
    sum[pos] = v;
    build(pos - 1); // 左子树
    build(pos + 1); // 右子树
}

int main() {
    int kase = 0;
    while(init()) {
        int p = 0;
        while(sum[p] == 0) p++; // 找最左边的叶子

        // 开始输出。因为要避免行末多余空格，所以稍微麻烦一点
        cout << "Case " << ++kase << ":\n" << sum[p++];
        while(sum[p] != 0) {
            cout << " " << sum[p];
            p++;
        }
        cout << "\n\n";
    }
    return 0;
}

Quadtree @

ch6, page160.

题意：给两棵四分树的先序遍历，求二者合并之后（黑色部分合并）黑色像素的个数。p 表示中间结点，f 表示黑色（full），e 表示白色（empty）

算法：先建树，然后统计

#include<cstdio>
#include<cstring>

const int len = 32;
const int maxn = 1024 + 10;
char s[maxn];
int buf[len][len], cnt;

// 把字符串 s[p..] 导出到以 (r,c) 为左上角，边长为 w 的缓冲区中
// 2 1
// 3 4
void draw(const char* s, int& p, int r, int c, int w) {
    char ch = s[p++];
    if(ch == 'p') {
        draw(s, p, r,     c+w/2, w/2); // 1
        draw(s, p, r,     c    , w/2); // 2
        draw(s, p, r+w/2, c    , w/2); // 3
        draw(s, p, r+w/2, c+w/2, w/2); // 4
    } else if(ch == 'f') { // 画黑像素（白像素不画）
        for(int i = r; i < r+w; i++)
            for(int j = c; j < c+w; j++)
                if(buf[i][j] == 0) { buf[i][j] = 1; cnt++; }
    }
}

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        memset(buf, 0, sizeof(buf));
        cnt = 0;
        for(int i = 0; i < 2; i++) {
            scanf("%s", s);
            int p = 0;
            draw(s, p, 0, 0, len);
        }
        printf("There are %d black pixels.\n", cnt);
    }
    return 0;
}

Oil Deposits @

ch6, page162.

题意：输入一个字符矩阵，统计字符 @ 组成多少个四连块

input:

    4   4                       # 4 行 4 列
    *   *   *   *   @
    *   @   @   *   @
    *   @   *   *   @
    @   @   @   *   @
    @   @   *   *   @

output:

    2

#include<cstdio>
#include<cstring>
const int maxn = 100 + 5;
char pic[maxn][maxn];
int m, n, idx[maxn][maxn];

void dfs( int r, int c, int id ) {
    if( r < 0 || r >= m || c < 0 || c >= n ) { return; }
    if( idx[r][c] > 0  || pic[r][c] != '@' ) { return; }
    idx[r][c] = id;
    for( int dr = -1; dr <= 1; dr++ ) {
        for( int dc = -1; dc <= 1; dc++ ) {
            if( dr != 0 || dc != 0 ) {
                dfs( r+dr, c+dc, id );
            }
        }
    }
}

int main() {
    while( scanf("%d%d", &m, &n) == 2 && m && n ) {
        int i = 0;
        char c;
        while( i < m*n && (c = getchar()) != EOF ) {
            if( c != '*' && c != '@' ) {
                continue;
            } else {
                pic[i/n][i%n] = c;
                ++i;
            }
        }
        memset( idx, 0, sizeof(idx) );
        int cnt = 0;
        for( int i = 0; i < m; ++i ) {
            for(int j = 0; j < n; ++j ) {
                if( idx[i][j] == 0 && pic[i][j] == '@' ) {
                    dfs( i, j, ++cnt );
                }
            }
        }
        printf( "%d\n", cnt );
    }
    return 0;
}

求多维数组连通块的过程也称为种子填充（floodfill）。

Ordering Tasks @

二元组 (u, v)，构造有向图，如果有环，关系“破裂”。

// UVa10305 Ordering Tasks
// Rujia Liu
// 题意：输入 n 和 m，以及 m 个二元组 (i,j)，求 1~n 的一个排列使得对于每个 (i,j)，i 在 j 的前面
// 算法：拓扑排序。注意 m 可能等于 0
#include <cstdio>
#include <cstring>
const int maxn = 1000;
int n, m, G[maxn][maxn], c[maxn], topo[maxn], t;

bool dfs( int u ) {
    c[u] = -1;
    for( int v = 0; v < n; v++ ) {
        if( G[u][v] ) {
            if( c[v]<0 ) { return false; }
        } else {
            if( !c[v]  ) { dfs(v); }
        }
    }
    c[u] = 1; topo[--t] = u;
    return true;
}

bool toposort() {
    t = n;
    memset( c, 0, sizeof(c) );
    for( int u = 0; u < n; u++) {
        if( !c[u] && !dfs(u) ) {
            return false;
        }
    }
    return true;
}

int main() {
    while( scanf("%d%d", &n, &m) == 2 && n ) {
        memset( G, 0, sizeof(G) );
        for( int i = 0; i < m; i++ ) {
            int u, v;
            scanf( "%d%d", &u, &v );
            G[u-1][v-1] = 1;
        }
        if( toposort() ) {
            for( int i = 0; i < n-1; i++ ) {
                printf("%d ", topo[i]+1);
            }
            printf("%d\n", topo[n-1]+1);
        } else {
            printf("No\n"); // 题目没说无解输出什么，应该是保证有解吧
        }
    }
}

$ cat input.txt
5 3
2 1
4 2
3 2

3 3
3 2
2 1
1 3

$ cat input.txt | ./a.out
1 1 1 1 5
No

Play on Words @

// UVa10129 Play on Words
// Rujia Liu
// 题意：输入 n 个单词，是否可以排成一个序列，使得每个单词的第一个字母和上一个单词的最后一个字母相同
// 算法：把字母看作结点，单词看成有向边，则有解当且仅当图中有欧拉路径。注意要先判连通

#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;

const int maxn = 1000 + 5;

// 并查集
int pa;
int findset(int x) { return pa[x] != x ? pa[x] = findset(pa[x]) : x; }
int used, deg;                                // 是否出现过；度数

int main() {
    int T;
    scanf( "%d", &T );
    while( T-- ) {
        int n;
        char word[maxn];

        scanf("%d", &n);
        memset(used, 0, sizeof(used));
        memset(deg, 0, sizeof(deg));
        for(int ch = 'a'; ch <= 'z'; ch++) pa[ch] = ch;
        int cc = 26;                                        // 连通块个数

        for(int i = 0; i < n; i++) {
            scanf("%s", word);
            char c1 = word, c2 = word[strlen(word)-1];
            deg[c1]++;
            deg[c2]--;
            used[c1] = used[c2] = 1;
            int s1 = findset(c1), s2 = findset(c2);
            if(s1 != s2) { pa[s1] = s2; cc--; }
        }

        vector<int> d;
        for(int ch = 'a'; ch <= 'z'; ch++) {
            if(!used[ch]) cc--;                               // 没出现过的字母
            else if(deg[ch] != 0) d.push_back(deg[ch]);
        }
        bool ok = false;
        if(cc == 1 && (d.empty() || (d.size() == 2 && (d == 1 || d == -1)))) ok = true;
        if(ok) printf("Ordering is possible.\n");
        else printf("The door cannot be opened.\n");
    }
    return 0;
}

$ cat input.txt
2
3
acm
malform
mouse
3
ack
malform
mouse

$ cat input.txt | ./a.out
Ordering is possible.
The door cannot be opened.

6-17 UVa10562 Undraw the Trees UVa10562.cpp
6-18 UVa12171 Sculpture UVa12171.cpp
6-19 UVa1572 Self-Assembly UVa1572.cpp

6-20 UVa1599 Ideal Path UVa1599.cpp ♥️ @

n 个点，m 条边（2<=n<=100000，1<=m<=200000）的无向图，每天边上都涂有一种颜色。求从节点 1 到节点 n 的一条路径，使得经过的边数尽量少，在此前提下，经过边的颜色序列的字典序最小。一对节点间可能有多条边，一条边，可能连接两个相同的结点。输入保证节点 1 可以达到节点 n。颜色为 1~10⁹ 的整数。

// UVa1599 Idea Path
// Rujia Liu
#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;

const int maxn = 100000 + 5;
const int INF = 1000000000; // maximal color

struct Edge {
    int u, v, c;
    Edge(int u=0, int v=0, int c=0):u(u),v(v),c(c) {}
};

vector<Edge> edges;
vector<int> G[maxn];

void AddEdge(int u, int v, int c) {
    edges.push_back(Edge(u, v, c));
    int idx = edges.size() - 1;
    G[u].push_back(idx);
}

int n, vis[maxn];
int d[maxn];
// reverse bfs to find out the distance from each node to n-1
void rev_bfs() {
    memset(vis, 0, sizeof(vis));
    d[n-1] = 0;
    vis[n-1] = true;

    queue<int> q;
    q.push(n-1);
    while(!q.empty()) {
        int v = q.front(); q.pop();
        for(int i = 0; i < G[v].size(); i++) {
            int e = G[v][i];
            int u = edges[e].v;
            if(!vis[u]) {
                vis[u] = true;
                d[u] = d[v] + 1;
                q.push(u);
            }
        }
    }
}

vector<int> ans;

// forward bfs to construct the path
void bfs() {
    memset(vis, 0, sizeof(vis));
    vis = true;
    ans.clear();

    vector<int> next;
    next.push_back(0);
    for(int i = 0; i < d; i++) {
        int min_color = INF;
        for(int j = 0; j < next.size(); j++) {
            int u = next[j];
            for(int k = 0; k < G[u].size(); k++) {
                int e = G[u][k];
                int v = edges[e].v;
                if(d[u] == d[v] + 1)
                    min_color = min(min_color, edges[e].c);
            }
        }
        ans.push_back(min_color);

        // find out the next vertices of the next phase
        vector<int> next2;
        for(int j = 0; j < next.size(); j++) {
            int u = next[j];
            for(int k = 0; k < G[u].size(); k++) {
                int e = G[u][k];
                int v = edges[e].v;
                if(d[u] == d[v] + 1 && !vis[v] && edges[e].c == min_color) {
                    vis[v] = true;
                    next2.push_back(v);
                }
            }
        }
        next = next2;
    }

    printf("%d\n", ans.size());
    printf("%d", ans);
    for(int i = 1; i < ans.size(); i++) printf(" %d", ans[i]);
    printf("\n");
}

int main() {
    int u, v, c, m;
    while(scanf("%d%d", &n, &m) == 2) {
        edges.size();
        for(int i = 0; i < n; i++) G[i].clear();
        while(m--) {
            scanf("%d%d%d", &u, &v, &c);
            AddEdge(u-1, v-1, c);
            AddEdge(v-1, u-1, c);
        }
        rev_bfs();
        bfs();
    }
    return 0;
}

6-21 UVa506 System Dependencies uva506.cpp
6-22 UVa11853 Paintball UVa11853.cpp

refs and see also

系统设计班 @

怎样设计 Facebook？理解 Google 的三驾马车！

无系统设计经验，或系统设计基础薄弱
现在实习生（Intern）都在面系统设计了你知道么？
希望知道怎样设计 Facebook Messenger? News Feed
希望知道怎样做一个爬虫系统
希望理解 Google 三驾马车
希望了解 NoSQL Database

✂️ 8/15/2016, 1:00:00 AM 走进系统设计 & 设计推特【免费试听】 @

什么是系统设计 What is System Design
系统设计中常见的问题是什么 How we ask System Design in Interview
怎样回答系统设计问题 How to answer System Design Question
系统设计的 4S 分析法 4S in System Design
系统设计的知识点构成 Basic Knowledge of System Design
设计推特 Design a Twitter

✂️ 8/21/2016, 1:00:00 AM 数据库系统 Database System @

通过设计聊天系统 Whatsapp 了解：

用户系统设计
聊天系统的核心设计点
数据库系统的相关知识
NoSQL 与 SQL 数据库的优劣比较与选取标准
一致性哈希算法 Consistent Hashing
分片算法 Sharding

✂️ 8/22/2016, 1:00:00 AM 爬虫系统与搜索建议系统 Web Crawler & Google Suggestion @

通过对爬虫系统设计 (Web Crawler) 与搜索建议系统设计 (Google Suggestion) 了解如下内容：

多线程
生产者消费者模型
爬虫系统的演化：单线程，多线程，分布式
Trie 结构的原理及应用
如何在系统设计中使用 Trie

✂️ 8/28/2016, 1:00:00 AM 分布式文件系统 & 设计查询系统 Google File System & Design Lookup Service @

以 GFS 为例系统学习 Google File System，并通过一道实战真题 Lookup Service 巩固要点，了解如下内容：

Master Slave 的设计模式
怎么处理分布式系统中的 failure 和 recovery 的问题.
如何做 replica, check sum 检查
了解 consistent hash 和 sharding 的实际应用

✂️ 8/29/2016, 1:00:00 AM, Web System & Design Tiny Url 网站系统设计 & 设计短网址系统 @

实战真题

What happend if you visit www.google.com?
How to design tiny url?
How to design rate limiter?
How to design data dog?

关键词：Web, Consistent Hashing, Memcached, Tiny url.

✂️ 9/04/2016, 1:00:00 AM, Big Table 原理透析 @

通过设计分布式数据库系统 Bigtable 了解如下内容：

Big Table 的原理与实现
了解 NoSQL Database 如何进行读写操作的, 以及相应的优化
了解如何建立 index
学习 Bloom Filter 的实现原理

✂️ 9/05/2016, 1:00:00 AM, Map Reduce & Design WhatsApp @

学习 Map Reduce 的应用与原理

了解如何多台机器并行解决算法问题
掌握 Map 和 Reduce 的原理
通过三个题目掌握 MapReduce 算法实现：
- WordCount
- InvertedIndex
- Anagram

设计聊天系统 Whatsapp

聊天系统中的 Pull vs Push
讲解一种特殊的 Service - Realtime Service

✂️ 9/11/2016, 1:00:00 AM, 基于地理位置信息的系统设计 Location Based Service @

系统学习 LBS 相关系统设计的核心要点：

地理位置信息存储与查询常用算法之 Geohash
如何设计 Yelp
如何设计 Uber
如何设计 Facebook Nearby

refs and see also

系统设计班 - 硅谷顶尖 IT 企业一线工程师直播教学

Programming Pearls @

part-1: preliminaries @
Basics of programming.
- column-1: cracking the oyster @
  
  磁盘排序：对于一个提出的问题，不要未经思考就直接给出答案。要先深入研究问题，搞清楚这个问题的特点，根据这个特点，可能有更好的解决方案。然后用了 bitmap。
  
  // init for i = [0, n) bit[i] = 0 // assign for each i in the input file bit[i] = 1 for i = [0, n) if bit[i] == 1 write i on the output file
  
  首先你要找到 the right problem。
  
  the bitmap data structure：a dense set over a finite domain
  
  multiple-pass algorithms: 多次读入输入，每次离目标近一点
  
  a time-space tradeoff and one that isn’t
  
  a simple design：不多不少刚刚好，简单的设计 bug 少
  
  stages of program design
- column-2: aha! alogrithms @
  
  经典问题：找数字 @
  
  给定一个包含 32 位整数的顺序文件 (sequential file)，它至多只能包含 40 亿 (4 billion) 个这样的整数，并且整数的次序是随机的 (in a random order)。请查找一个此文件中不存在的 32 位整数。在有足够内存的情况下 (with ample quantities of main memory)，你会如何解决这个问题？如果你可以使用若干外部临时文件但可用主存却只有上百字节，你会如何解决这个问题？
  
  Given a sequential file that contain at most 4x109 integers(32-bit) in random order, find a 32-bit integer that is not in the file.
  
  How would you solve it with ample main memory? – bitmap (232 bits)
  
  or using several external “scratch” files but only a few hundred bytes of main memory? – binary search 二分查找
  
  首先，只是说找一个。其实 missing 的有很多==（因为 32 bit 的整数有 2^32 (4,294,967,296)个，这里只有 4 billion 个数字，肯定有一些数没有。）
  
  4 billion 内的数字都可以用 int 来表示，所以用 bitmap 的话，有 2^32 个 bit 就够了，也就是 2^{32}/8 bytes = 2^{32-3=29=9+10+10} bytes = 2^9 MBytes = 512 MBytes.
  
  类似二分查找。可以根据某一位（操作时，可以从最高位到最低位依次处理），把待处理的数据分成两部分。在一部分中，此位为 0，另一部分此位为 1。
  
  之后，分别统计落在两个部分的数的个数。（此时我们不考虑数据是否重复）
  
  如果，没有缺失，那么这两部分数的个数应该是相等的。
  
  如果，数据有缺失，那么两部分数可能相等，也可能不等
  
  两部分相等的情况：两段都缺失，但缺失的个数相等
  
  两部分不等的情况：一个缺一个不缺或都缺但缺的个数不同
  
  Reverse, n=8, i=3, abcdefgh -> defghabc @
  
  reverse( 0, i-1 ); // cbadefgh reverse( i, n-1 ); // cbahgfed reverse( 0, n-1 ); // defghabc
  
  作者还很巧妙的用翻手来解释这个方案。
  
  这个 reverse 可以这个写：（两边都是闭区间，[left, right]）
  
  // method 1 void reverse( char *str, int start, int end ) { char tmp; int mid = (start + end)/2; for ( int i = start, j = end; i <= mid; ++i, --j ) { tmp = str[i]; str[i] = str[j]; str[j] = tmp; } } // method 2, I prefer this one void reverse( char *str, int start, int end ) { char tmp; while( start < end ) { tmp = str[start]; str[start] = str[end]; str[end] = tmp; ++start; --end; } } // 但不管怎样，调用的时候不要把 reverse( str, 0, strlen(str)-1 ); // 写成 reverse( str, 0, strlen(str) ); // 闭区间啊，同学！
  
  signature 的重要性，pots, stop, tops @
  
  找 signature 是最重要的。
  
  原则：
  
  sorting
  
  binary search
  
  signatures
  
  Problems
  
  翻转句子中单词的顺序，但单词内字符的顺序不变 @
  
  句子中单词以空格符隔开。为简单起见，标点符号和普通字母一样处理。
  
  方法：先分别对各个单词进行逆转，然后对整个句子进行逆转。
  
  I love you. -> I evol .uoy -> you. love I
  
  #include <stdio.h> #include <string.h> void reverse( char *s, int left, int right ) { char tmp; while( left < right ) { tmp = s[left]; s[left] = s[right]; s[right] = tmp; ++left; --right; } } void solve( char *s ) { int left = 0, right = 0, len = strlen(s); while( left < len && right < len ) { while( s[right] && s[right] != ' ' ) { ++right; } if( !s[right] && left < right-1 ) { reverse( s, left, right-1 ); // 最后一段 break; } reverse( s, left, right-1 ); left = right + 1; // 跳过连续空格 while( s[left] == ' ' ) { ++left; } right = left + 1; } reverse( s, 0, len-1 ); // 这个 len-1 千万不能是 len } int main() { char buf; sprintf( buf, "%s", "I love Sia Furler." ); printf( "before: %s\n", buf ); solve( buf ); printf( "%s\n", buf ); }
  
  Furler. Sia love I
  
  类似手机键盘
  
  每个数字对应几个字母。按下数字键，就意味着多个字符组合，有关这些字符组合的姓名和手机号就找到。问题，如何实现一个以名字的按键编码为参数，并返回所有可能的匹配名字的函数
  
  方法：把名字对应的数字按键形成一个唯一的标识符，值存入数字键对应的名字 map<int,map<string> > rec;
  
  sequential file 里的 4,300,000,000 个 32-bit integers 中找 one that appears at least twice？
- column-3: data structures programs @
  
  if( k == 500 ) c500++;……如此蛋疼的代码。
  
  信件模板。
  
  Principles
  
  Don’t write a big program when a little one will do.
  
  使用数组重新编写重复代码。
  
  封装复杂结构。
  
  尽可能使用高级工具。名字-值对，电子表格（二维数组），数据库，特定编程语言的强大的工具。
  
  从数据得出程序的结构。(let data structure the program.)
- column-4: writing correct programs @
  
  Knuth 说，46 年 binary search 的论文出来了，62 年，终于有一个 bug free 的实现==。
  
  本章作者主要证明了二分搜索程序的正确性。
  
  构造程序的正确性上来先要找到断言(assertions)，也就是所谓的【循环不变式】，当然这个在实际程序中，只有靠经验了。找到断言，即可以勾勒出，输入、程序变量和输出之间的关系，使得程序员可以准确阐述这些关系。拿二分来说，就是如果元素 t 在数组中，那么它一定在 range 中。在之后所有的操作都要遵循该不变式。
  
  接下来看程序的结构。
  
  如果是顺序控制结构 (sequential control structures)。则可以通过在语句之间添加断言并分别分析程序执行的每一步。
  
  如果是选择控制结构 (selection control structures)，则要对每一个分支进行结构的正确性证明。选择每一个分支，使用断言来证明。例如，如果进入了 if i > j 的分支，那么我们就可以断言 i > j 并且使用这个事实来推倒出下一个断言。
  
  最麻烦就是迭代控制结构 (iteration control structures)。要证明循环的正确性，就必须为其确立 3 个性质。
  
  初始化 (initialization)：循环初次执行的时候不变式为真。
  
  保持 (preservation)：如果在某次迭代开始的时候以及循环体执行的时候，不变式为真，那么循环执行完毕的时候不变式仍然为真。每次迭代都保持该不变式为真。
  
  终止 (termination)：循环能够终止，并且可以得到预期的结果，而且我们必须用其他方法证明循环一定能终止。就像二分每次范围都在减少，课后习题，豆子每次都在减少一个。
  
  对于函数的正确性证明，首先要使用两个断言来陈述目的。
  
  前置条件：调用该函数之前成立的状态。
  
  后置条件的正确性由函数在终止时保证。
  
  拿二分来说，前置条件是序列有序（二分），后置条件是找没有找到元素，返回位置。
  
  如果在前置条件满足情况下调用函数，那么函数的执行将确立后置条件，这就是契约编程。
  
  证明程序的正确性是一门学问，如果违反断言就指明了程序的错误所在。程序状态的断言对理解程序很有帮助。
  
  int binary_search( int A[], int n, int target ) { int low = 0, high = n-1; // 注意不是 n，因为 low 和 high 都是闭区间的端点。 int mid; while( low <= high ) { mid = (low+high)/2; if( A[mid] < target ) { low = mid+1; } else if( A[mid] > target ) { high = mid-1; } else { return mid; } } return -1; }
- column-5: a small matter of programming @
  
  主要讲解如何保证编程的正确性。在程序中加入断言（assert(断言内容) //如果错误，则终止程序。否则正常执行））。
  
  一些 debug 技巧？assert 什么的使用，自动化测试。
part-2: performance @
向性能前进！
- column-6: perspective on performance @
  
  如果要提高软件的性能，需要从下面几个方面入手：
  
  算法与数据结构
  
  算法调优
  
  数据结构重组
  
  与系统无关的代码的调优（float 取代 double）。
  
  与系统相关的调优，把经常使用的函数进行加速，比如关键代码使用汇编代替高级语言
  
  硬件上使用浮点加速器。
- column-7: the back of the envelope @
  
  密西西比河一天流出多少水？
  
  量纲检验：即在检验几何或物理等式时，我们可以先看看其中的单位在乘除过后是否与原式能保持一致。
  
  模 9 法（舍 9 法）：在加法计算当中，加数的数字总和与和数的数字总和模 9 相等。举个例子：3142+2718+1123=6973. （3+1+4+2+2+7+1+8+1+1+2+3）%9=7=（6+9+7+3）%9.
  
  72 法则
  
  “假设以年利率 r% 投资一笔钱 y 年，如果 r×y=72，那么你的投资差不多会翻倍。”比如年利率 6% 投资 1000 美元 12 年，可以得到 2012 美元。很有意思～
  
  假设一个程序 n=40 时需要 10 秒，并且 n 增加 1，时间就增加 12%，根据 72 法则，每当 n 增加 6，运行时间就加倍，n 每增加 60，运行时间就是原来的 1000 倍（n 增加 60，也就是说翻 10 倍，2 的 10 次方是 1024）
  
  tip：π秒 = 1 纳世纪秒 = 10^-9 * 100 s = 10^-7 s
  
  一年有 pi * 10^7 秒。
  
  pi×10⁷ = 2^1.65×10×10⁶ = 2^1.65+3.3+20 = 2^24.95
  
  一分钟等于 60s（2^5.9s），一小时 60²s（2^11.8s），一天有 60²×24s（2^11.82^4.6 = 2^16.4）s。一年就有 2^16.4×28.5^ = 2^24.9。
  
  Rule of thumb - Wikipedia, the free encyclopedia
  
  Statistical – Rule of 72: A rule of thumb for exponential growth at a constant rate. An approximation of the doubling time formula used in population growth, according to which the doubling time is roughly equal to 70 divided by the percent growth rate (using continuous compounding, the actual number would be about 69.31 or 100 times the natural logarithm of 2). In terms of money, since most people use the annual effective interest rate (which is equivalent to annual compounding) for interest rates between 4% and 12%, the number that gives the most accurate result is actually 72. Therefore, one may divide 72 by the percent interest rate to determine the approximate amount of time it would take to double one’s money in an investment. For example, at 8% interest, the investment will double in approximately 9 years (72/8 = 9).
  
  Rule of 72 - Wikipedia, the free encyclopedia @
  
  For instance, if you were to invest $100 with compounding interest at a rate of 9% per annum, the rule of 72 gives 72/9 = 8 years required for the investment to be worth $200; an exact calculation gives ln(2)/ln(1+.09) = 8.0432 years.
  
  To determine the time for money’s buying power to halve, financiers simply divide the rule-quantity by the inflation rate. Thus at 3.5% inflation using the rule of 70, it should take approximately 70/3.5 = 20 years for the value of a unit of currency to halve.
  
  安全系数
  
  作者强调安全性，并且举了一个例子。一个建筑工程师对于桥建筑的破环函数的数学公式不懂（对于桥来说，风力、震动等破环因子都可以通过复杂的数学公式推导出来），于是他设想他的桥会遭受到正常破环的 6 倍。结果是与他同时期建造的桥全部倒塌，只有他的桥屹立不倒。
  
  “我们是和 john Roebling(文中的建筑工程师) 一样的工程师么？我很怀疑”
  
  Little定律
  
  Denning 和 Buzen 介绍的 Little 定律“系统中物体的平均数量等于物体离开系统的平均速率和每个物体在系统中停留的平均时间的乘积（并且如果物体离开和进入系统的通体出入流是平衡的，那么离开速率也就是进入速率。）”书中举了个例子，假如你要进入一个火爆的夜总会（美国电影中经常见到），“这个地方可以容纳约 60 人，每个人在里面逗留的时间大约是 3 小时，因此我们进入夜总会的速率大概是每小时 20 人，现在在队伍中我们前面还有 20 人，也就是说我们要等大约 1 个小时，不如我们回家去读《编程珠玑》吧。”哈哈
  
  在进行粗略估算的时候，要切记爱因斯坦的名言：
  
  任何事都应尽量简单，但不宜过于简单。
- column-8: algorithms design techniques @
  
  【编程珠玑】第八章算法设计技术 - 小田的专栏 - 博客频道 - CSDN.NET
- column-9: code tuning @
  
  最后，作者讲到，对于代码调优最重要的原则就是尽量少用它。作者从效率的角色、度量工具、设计层面、双刃剑几个方面分析了代码调优的优劣两面性。回归到一点，就是对于一个优秀的程序员，不论是在程序维护，程序可靠性，还是程序的效率方面，都不能只顾一头，而是要尽量做一个综合的评估再根据实际需求进行取舍。
  
  【编程珠玑】第九章代码调优 - 小田的专栏 - 博客频道 - CSDN.NET
- column-10: squeezing space @
  
  【编程珠玑】第十章节省空间 - 小田的专栏 - 博客频道 - CSDN.NET
  
  principles
  
  the cost of space
  
  the “hot spot” of space (哪里是耗时最长的？)
  
  measuring space
  
  tradeoffs
  
  work with the environment
  
  use the right tool fo the job.
part-3 @
- column-11: sorting @
  
  编程珠玑第十一章—-排序 - dazhong159的专栏 - 博客频道 - CSDN.NET
- column-12: a sample problem
- column-13: searching
- column-14: heaps
- column-15: strings of pearls

refs and see also @

VisuAlgo - visualising data structures and algorithms through animation @

冒泡排序 @

大泡泡飘上去。
选择排序 @

选择一个 pivot 来比。然后更新。
插入排序 @

左边是排好的，不断把右边没有排好的插入进去。注意移位的时候 i 和 j。
归并排序 @
快排 @
随机快排 @
计数排序 @
基数排序 @
create binary heap @
heap sort @
MISC @

refs and see also

VisuAlgo - visualising data structures and algorithms through animation

Beauty of Programming @

#include <stdio.h>

int main() {
    int i = 81;
    while( i-- ) {
        if( i/9%3 == i%9%3 ) { continue; }
        printf( "A = %d, B = %d\n", i/9+1, i%9+1 );
    }
}

#include <stdio.h>

struct {
    unsigned char a:4;
    unsigned char b:4;
} i;

for( i.a = 1; i.a <= 9; ++i.a ) {
    for( i.b = 1; i.b <= 9; ++i.b ) {
        if( i.a%3 != i.b%3 ) {
            printf( "A = %d, B = %d\n", i.a, i.b );
        }
    }
}

XOR

#include <stdio.h>

int main() {
    int A[] = { 1, 2, 1, 3, 8, 8, 3, 9, 0, 9 }; // 0!
    int x = 0;
    for( int i =0; i < sizeof(A)/sizeof(A[0]); ++i ) {
        x ^= A[i]; // communitive rule, xor
    }
    printf( "the missing one is: %d\n", x );
}

2.

常见 C/C++ 函数 @

size_t strlen( const char *str ) @

size_t strlen( const char *str )
{
    const char *s = str;
    while( *s ) { ++s; }
    return s-str;
}

不要把 while( *s ) { ++s; } 写成 while( *s++ ) { }

然而这里却可以把 ++ 写在 while 的判断里面：

size_t strlen( const char *str )
{
    size_t i = 0;
    while( *str++ ) { ++i; }
    return i;
}

函数签名可以在 man strlen 或者 man 3 strlen 看到。

或者用 for 循环：

size_t strlen( const char *str ) {
    const char *s;
    for ( s = str; *s; ++s ) {}
    return (s - str);
}

char * strcpy( char *to, const char *from ) @
```
char * strcpy( char *to, const char *from  )
{
    if ( !from && !to ) { return NULL; }
    char *p = to;
    while( (*p++=*from++) != 0 ) { }
    return to;
}
```
前面的判断似乎多余，因为我们不关心 to 是否有空间以及它原来的内容，我们也不需要知道 from 是否为 NULL（如果 NULL，那在 while 里面复制一个 NULL 就结束，也是符合预期的。）

int atoi( const char *str) @

int atoi( const char *str )
{
    // TODO: handle overflow
    if ( !str ) { return 0; }

    int len = strlen( str );
    int sign = 1;

    const char *p = str;
    while ( *p == ' ' ) {
        ++p;
    }

    if ( *p == '+' ) { sign = +1; ++p; }
    if ( *p == '-' ) { sign = -1; ++p; }

    int i = 0;
    while( p && '0' <= *p && *p <= '9' ) {
        i = i * 10 + (*p - '0');
        ++p;
    }

    return i*sign;
}

int atoi( const char *str )
{
    const char *p = str;
    while ( *p == ' ' ) { ++p; }

    int sign = 1;
    if ( *p == '+' ) { sign = +1; ++p; }
    if ( *p == '-' ) { sign = -1; ++p; }

    int num = 0;
    while( '0' <= *p && *p <= '9' ) {
        // buggy here: -2^31 ~ 2^31-1, it's not symmetric
        if( num > INT_MAX / 10 || (num == INT_MAX/10 && (*p-'0')>INTMAX%10 ) {
            return sign == -1 ? INT_MIN : INT_MAX;
        }
        num = num * 10 + (*p - '0');
        ++p;
    }

    return sign*num;
}

see LeetCode String to Integer (atoi), http://leetcode.com/oldoj#question_8.

const char * convert( char buf[], int value ) @

#include <iostream>
#include <algorithm>
#include <stdio.h>

const char* convert( char buf[], int value )
{
    static char digits =
    { '9', '8', '7', '6', '5', '4', '3', '2', '1', '0',
        '1', '2', '3', '4', '5', '6', '7', '8', '9' };
    static const char *const zero = digits + 9; // zero 指向 '0'
    // works for -2147483648 .. 2147483647
    int i = value;
    char* p = buf;
    do {
        // lsd - least significant digit
        int lsd = i % 10; // lsd 可能小于 0
        // 是向下取整还是向零取整?
        *p++ = zero[lsd]; // 下标可能为负
        i /= 10;
    } while (i != 0);
    if (value < 0) {
        *p++ = '-';
    }
    *p = '\0';
    std::reverse(buf, p);
    return p; // p - buf 即为整数长度
}

int main() {
    char buf;
    int num;
    while( 1 == scanf( "%d", &num ) ) {
        convert( buf, num );
        printf( "%d -> \"%s\"\n", num, buf );
    }
}

上面的代码来自 chenshuo，但我总觉得这 19 个 digits 把事情弄复杂了。我的策略是，负数我就把它先转成正数：

const char* convert( char buf[], int value )
{
    if( value < 0 ) {
        buf = '-';
        return convert( buf+1, -value );
    }

    static char zero = { '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' };

    char* p = buf;
    do {
        *p++ = zero[value%10];
        value /= 10;
    } while (value != 0);
    *p = '\0';
    std::reverse(buf, p);
    return p;
}

char * strchr( const char *s, int c ) @

char * strchr( const char *s, int c )
{
    while( *s ) {
        if( *s == c ) {
            return s;
        } else {
            ++s;
        }
    }
    return s;
}

目测没有 bug。懒得测了。

char * strstr( const char *haystack, const char *needle) @

char *strstr(const char *haystack, const char *needle) {
    // if needle is empty return the full string
    if (!*needle) return (char*) haystack;

    const char *p1;
    const char *p2;
    const char *p1_advance = haystack;
    for (p2 = &needle; *p2; ++p2) {
        p1_advance++;   // advance p1_advance M-1 times
    }

    for (p1 = haystack; *p1_advance; p1_advance++) {
        char *p1_old = (char*) p1;
        p2 = needle;
        while (*p1 && *p2 && *p1 == *p2) {
            p1++;
            p2++;
        }
        if (!*p2) return p1_old;

        p1 = p1_old + 1;
    }
    return NULL;
}

see also KMP.

TODO: strncpy, strcmp, strcat @

char * __cdecl strcat (char * dst,const char * src)
{
    char * cp = dst;

    while( *cp )
        cp++;                   /* find end of dst */

    while( *cp++ = *src++ ) ;       /* Copy src to end of dst */

    return( dst );                  /* return dst */

}

int __cdecl strcmp (const char * src,const char * dst)
{
    int ret = 0 ;

    while( ! (ret = *(unsigned char *)src - *(unsigned char *)dst) && *dst)
        ++src, ++dst;

    if ( ret < 0 )
        ret = -1 ;
    else if ( ret > 0 )
        ret = 1 ;

    return( ret );
}

size_t __cdecl strlen (const char * str)
{
    const char *eos = str;

    while( *eos++ ) ;

    return( (int)(eos - str - 1) );
}

char * __cdecl strncat (char * front,const char * back,size_t count)
{
    char *start = front;

    while (*front++)
        ;
    front--;

    while (count--)
        if (!(*front++ = *back++))
            return(start);

        *front = '\0';
        return(start);
}

int __cdecl strncmp (const char * first,const char * last,size_t count)
{
    if (!count)
        return(0);

    while (--count && *first && *first == *last)
    {
        first++;
        last++;
    }

    return( *(unsigned char *)first - *(unsigned char *)last );
}

/* Copy SRC to DEST.  */
char *
strcpy (dest, src)
char *dest;
const char *src;
{
    reg_char c;
    char *__unbounded s = (char *__unbounded) CHECK_BOUNDS_LOW (src);
    const ptrdiff_t off = CHECK_BOUNDS_LOW (dest) - s - 1;
    size_t n;

    do
    {
        c = *s++;
        s[off] = c;
    }
    while (c != '\0');

    n = s - src;
    (void) CHECK_BOUNDS_HIGH (src + n);
    (void) CHECK_BOUNDS_HIGH (dest + n);

    return dest;
}

char * __cdecl strncpy (char * dest,const char * source,size_t count)
{
    char *start = dest;

    while (count && (*dest++ = *source++))    /* copy string */
        count--;

    if (count)                              /* pad out with zeroes */
        while (--count)
            *dest++ = '\0';

        return(start);
}

refs and see also

程序员编程艺术：第四章、现场编写类似 strstr/strcpy/strpbrk 的函数 - 结构之法算法之道 - 博客频道 - CSDN.NET

StackOverflow ♥️ @

logic - What is the optimal algorithm for the game 2048? - Stack Overflow
algorithm - What is a plain English explanation of “Big O” notation? - Stack Overflow
c++ - Image Processing: Algorithm Improvement for ‘Coca-Cola Can’ Recognition - Stack Overflow @

signature scan lines.
algorithm - What is tail recursion? - Stack Overflow @
```
def recsum(x):
    if x == 1:
        return x
    else:
        return x + recsum(x - 1)
```
In traditional recursion, the typical model is that you perform your recursive calls first, and then you take the return value of the recursive call and calculate the result. In this manner, you don’t get the result of your calculation until you have returned from every recursive call.

In tail recursion, you perform your calculations first, and then you execute the recursive call, passing the results of your current step to the next recursive step. This results in the last statement being in the form of “(return (recursive-function params))” (I think that’s the syntax for Lisp). Basically, the return value of any given recursive step is the same as the return value of the next recursive call.

The consequence of this is that once you are ready to perform your next recursive step, you don’t need the current stack frame any more. This allows for some optimization. In fact, with an appropriately written compiler, you should never have a stack overflow snicker with a tail recursive call. Simply reuse the current stack frame for the next recursive step. I’m pretty sure Lisp does this.

An important point is that tail recursion is essentially equivalent to looping.
algorithm - Easy interview question got harder: given numbers 1..100, find the missing number(s) - Stack Overflow @

Newton’s identities - Wikipedia, the free encyclopedia
search - Ukkonen’s suffix tree algorithm in plain English? - Stack Overflow
algorithm - Find an integer not among four billion given ones - Stack Overflow @
Given an input file with four billion integers, provide an algorithm to generate an integer which is not contained in the file. Assume you have 1 GB memory. Follow up with what you would do if you have only 10 MB of memory.

Assuming that “integer” means 32 bits

Having 10 MB of space is more than enough for you to count how many numbers there are in the input file with any given 16-bit prefix, for all possible 16-bit prefixes in one pass through the input file. At least one of the buckets will have be hit less than 2^16 times. Do a second pass to find of which of the possible numbers in that bucket are used already.

If it means more than 32 bits, but still of bounded size

Do as above, ignoring all input numbers that happen to fall outside the (signed or unsigned; your choice) 32-bit range.

If “integer” means mathematical integer

Read through the input once and keep track of the largest number length of the longest number you’ve ever seen. When you’re done, output the maximum plus one a random number that has one more digit. (One of the numbers in the file may be a bignum that takes more than 10 MB to represent exactly, but if the input is a file, then you can at least represent the length of anything that fits in it).
```
#define BITSPERWORD 32
#define SHIFT 5
#define MASK 0x1F
#define N 10000000
int a[1 + N/BITSPERWORD];

void set(int i) {        a[i>>SHIFT] |=  (1<<(i & MASK)); }
void clr(int i) {        a[i>>SHIFT] &= ~(1<<(i & MASK)); }
int  test(int i){ return a[i>>SHIFT] &   (1<<(i & MASK)); }
```
algorithm - What are the differences between NP, NP-Complete and NP-Hard? - Stack Overflow @
Decision problem

A problem with a yes or no answer.

Now, let us define those complexity classes.
P

P is a complexity class that represents the set of all decision problems that can be solved in polynomial time. That is, given an instance of the problem, the answer yes or no can be decided in polynomial time.

Example

Given a graph connected G, can its vertices be coloured using two colours so that no edge is monochromatic?

Algorithm: start with an arbitrary vertex, color it red and all of its neighbours blue and continue. Stop when you run out of vertices or you are forced to make an edge have both of its endpoints be the same color.

NP

NP is a complexity class that represents the set of all decision problems for which the instances where the answer is “yes” have proofs that can be verified in polynomial time.

This means that if someone gives us an instance of the problem and a certificate (sometimes called a witness) to the answer being yes, we can check that it is correct in polynomial time.

Example

Integer factorisation is in NP. This is the problem that given integers n and m, is there an integer f with 1 < f < m, such that f divides n (f is a small factor of n)?

This is a decision problem because the answers are yes or no. If someone hands us an instance of the problem (so they hand us integers n and m) and an integer f with 1 < f < m, and claim that f is a factor of n (the certificate), we can check the answer in polynomial time by performing the division n / f.

NP-Complete
NP-Complete is a complexity class which represents the set of all problems X in NP for which it is possible to reduce any other NP problem Y to X in polynomial time.

Intuitively this means that we can solve Y quickly if we know how to solve X quickly. Precisely, Y is reducible to X, if there is a polynomial time algorithm f to transform instances y of Y to instances x = f(y) of X in polynomial time, with the property that the answer to y is yes, if and only if the answer to f(y) is yes.

Example

3-SAT. This is the problem wherein we are given a conjunction (ANDs) of 3-clause disjunctions (ORs), statements of the form

(x_v11 OR x_v21 OR x_v31) AND (x_v12 OR x_v22 OR x_v32) AND ... AND (x_v1n OR x_v2n OR x_v3n)

where each x_vij is a boolean variable or the negation of a variable from a finite predefined list (x_1, x_2, … x_n).

It can be shown that every NP problem can be reduced to 3-SAT. The proof of this is technical and requires use of the technical definition of NP (based on non-deterministic Turing machines). This is known as Cook’s theorem.

What makes NP-complete problems important is that if a deterministic polynomial time algorithm can be found to solve one of them, every NP problem is solvable in polynomial time (one problem to rule them all).
NP-hard

P = NP
```
____________________________________________________________
| Problem Type | Verifiable in P time | Solvable in P time | Increasing Difficulty
|______________|______________________|____________________|           |
| P            |        Yes           |        Yes         |           |
| NP           |        Yes           |     Yes or No *    |           |
| NP-Complete  |        Yes           |      Unknown       |           |
| NP-Hard      |     Yes or No **     |      Unknown ***   |           |
|______________|______________________|____________________|           V
```
algorithm - Big O, how do you calculate/approximate it? - Stack Overflow

algorithm - Calculate distance between two latitude-longitude points? (Haversine formula) - Stack Overflow @

// This script [in Javascript] calculates great-circle distances between the
// two points – that is, the shortest distance over the earth’s surface – using
// the ‘Haversine’ formula.
function getDistanceFromLatLonInKm(lat1,lon1,lat2,lon2) {
    var R = 6371; // Radius of the earth in km
    var dLat = deg2rad(lat2-lat1);  // deg2rad below
    var dLon = deg2rad(lon2-lon1);
    var a =
        Math.sin(dLat/2) * Math.sin(dLat/2) +
        Math.cos(deg2rad(lat1)) * Math.cos(deg2rad(lat2)) *
        Math.sin(dLon/2) * Math.sin(dLon/2)
        ;
    var c = 2 * Math.atan2(Math.sqrt(a), Math.sqrt(1-a));
    var d = R * c; // Distance in km
    return d;
}

function deg2rad(deg) {
    return deg * (Math.PI/180)
}

refs and see also

routing - What algorithms compute directions from point A to point B on a map? - Stack Overflow
c# - How to check if a number is a power of 2 - Stack Overflow @

x & (x-1) == 0 ?, as I expected.
algorithm - How to code a URL shortener? - Stack Overflow @
- encode, bijective.
- checksum
Algorithm to return all combinations of k elements from n - Stack Overflow @

chenshuo has a better solution.
sql - What is the most efficient/elegant way to parse a flat table into a tree? - Stack Overflow
algorithm - How to find list of possible words from a letter matrix [Boggle Solver] - Stack Overflow
c++ - Most effective way for float and double comparison - Stack Overflow
algorithm - Getting the closest string match - Stack Overflow @
- Levenshtein distance - Wikipedia, the free encyclopedia
c - Why doesn’t GCC optimize aaaaaa to (aaa)(aaa)? - Stack Overflow @
Because Floating Point Math is not Associative. The way you group the operands in floating point multiplication has an effect on the numerical accuracy of the answer.

As a result, most compilers are very conservative about reordering floating point calculations unless they can be sure that the answer will stay the same, or unless you tell them you don’t care about numerical accuracy. For example: the -fassociative-math option of gcc which allows gcc to reassociate floating point operations, or even the -ffast-math option which allows even more aggressive tradeoffs of accuracy against speed.

Another similar case: most compilers won’t optimize a + b + c + d to (a + b) + (c + d) (this is an optimization since the second expression can be pipelined better) and evaluate it as given (i.e. as (((a + b) + c) + d)). This too is because of corner cases:
```
#include <stdio.h>

int main() {
    float a = 1e35, b = 1e-5, c = -1e35, d = 1e-5;
    printf("%e %e\n", a + b + c + d, (a + b) + (c + d)); // 1.000000e-05 0.000000e+00
}
```
What Every Computer Scientist Should Know About Floating-Point Arithmetic

c - Divide a number by 3 without using *, /, +, -, % operators - Stack Overflow @

// replaces the + operator
int add(int x, int y) {
    while(x) {
        int t = (x & y) <<1;
        y ^= x;
        x = t;
    }
    return y;
}

int divideby3 (int num) {
    int sum = 0;
    while (num > 3) {
        sum = add(num >> 2, sum);
        num = add(num >> 2, num & 3);
    }
    if (num == 3)
        sum = add(sum, 1);
    return sum;
}

As Jim commented this works because:

n = 4 * a + b
n / 3 = a + (a + b) / 3
So sum += a, n = a + b, and iterate
When a == 0 (n < 4), sum += floor(n / 3); i.e. 1, if n == 3, else 0

How do you set, clear and toggle a single bit in C/C++? - Stack Overflow @
- set a bit: number |= 1 << x;
- clear a bit: number &= ~(1 << x);
- toggle a bit: number ^= 1 << x;
- checking a bit: bit = (number >> x) & 1;
- changing the nth bit to x: number ^= (-x ^ number) & (1 << n);
In C++ source, what is the effect of extern “C”? - Stack Overflow
c - How to initialize all members of an array to the same value - Stack Overflow @
refs and see also
- 不要被别人的 memset(buf, -1, sizeof(buf)) 迷惑了 · Issue #2 · district10/notes · GitHub
Why use apparently meaningless do-while and if-else statements in C/C++ macros? - Stack Overflow
c++ - std::next_permutation Implementation Explanation - Stack Overflow
how to find the intersection of two std:set in C++? - Stack Overflow
c++ - Why are std::shuffle methods being deprecated in C++14? - Stack Overflow
c++ - Composability of STL algorithms - Stack Overflow
C++ implementation explained - Stack Overflow
c++ - std::copy n elements or to the end - Stack Overflow

Milo Yip 的博客 ♥️ @

《编程之美: 求二叉树中节点的最大距离》的另一个解法 - Milo Yip - 博客园 @

书中对这个问题的分析是很清楚的，我尝试用自己的方式简短覆述。

计算一个二叉树的最大距离有两个情况:

情况 A: 路径经过左子树的最深节点，通过根节点，再到右子树的最深节点。
情况 B: 路径不穿过根节点，而是左子树或右子树的最大距离路径，取其大者。

只需要计算这两个情况的路径距离，并取其大者，就是该二叉树的最大距离。

这段代码有几个缺点:

算法加入了侵入式 (intrusive) 的资料 nMaxLeft, nMaxRight
使用了全局变量 nMaxLen。每次使用要额外初始化。而且就算是不同的独立资料，也不能在多个线程使用这个函数
逻辑比较复杂，也有许多 NULL 相关的条件测试。

我方知道這個「距離」應該是叫「直徑」(Tree Diameter)。的确是“直径”——在数学中直径的定义是：一个距离空间中任意两点间距离的上确界 (supremum)。

#include <iostream>
using namespace std;

struct NODE {
    NODE *pLeft;
    NODE *pRight;
};

struct RESULT {
    int nMaxDistance;
    int nMaxDepth;
};

RESULT GetMaximumDistance(NODE* root) {
    if (!root) {
        RESULT empty = { 0, -1 };   // trick: nMaxDepth is -1 and then caller will plus 1 to balance it as zero.
        return empty;
    }

    RESULT lhs = GetMaximumDistance(root->pLeft);
    RESULT rhs = GetMaximumDistance(root->pRight);

    RESULT result = {
        max(max(lhs.nMaxDistance, rhs.nMaxDistance), lhs.nMaxDepth + rhs.nMaxDepth + 2),
        max(lhs.nMaxDepth + 1, rhs.nMaxDepth + 1)
    };
    return result;
}

void Link(NODE* nodes, int parent, int left, int right) {
    if( left  != -1 ) { nodes[parent].pLeft = &nodes[left]; }
    if( right != -1 ) { nodes[parent].pRight = &nodes[right]; }
}

void main() {
    // P. 241 Graph 3-12
    NODE test1 = { 0 };
    Link(test1, 0, 1, 2);
    Link(test1, 1, 3, 4);
    Link(test1, 2, 5, 6);
    Link(test1, 3, 7, -1);
    Link(test1, 5, -1, 8);
    cout << "test1: " << GetMaximumDistance(&test1).nMaxDistance << endl;

    // P. 242 Graph 3-13 left
    NODE test2 = { 0 };
    Link(test2, 0, 1, 2);
    Link(test2, 1, 3, -1);
    cout << "test2: " << GetMaximumDistance(&test2).nMaxDistance << endl;

    // P. 242 Graph 3-13 right
    NODE test3 = { 0 };
    Link(test3, 0, -1, 1);
    Link(test3, 1, 2, 3);
    Link(test3, 2, 4, -1);
    Link(test3, 3, 5, 6);
    Link(test3, 4, 7, -1);
    Link(test3, 5, -1, 8);
    cout << "test3: " << GetMaximumDistance(&test3).nMaxDistance << endl;

    // P. 242 Graph 3-14
    // Same as Graph 3-2, not test

    // P. 243 Graph 3-15
    NODE test4 = { 0 };
    Link(test4, 0, 1, 2);
    Link(test4, 1, 3, 4);
    Link(test4, 3, 5, 6);
    Link(test4, 5, 7, -1);
    Link(test4, 6, -1, 8);
    cout << "test4: " << GetMaximumDistance(&test4).nMaxDistance << endl;
}

test1: 6
test2: 3
test3: 6
test4: 5

refs and see also

Tree Diameter

《编程之美：分层遍历二叉树》的另外两个实现 - Milo Yip - 博客园 @

（这篇 post 的内容已经被转入 jiuzhang。）

void PrintNodeByLevel(Node* root) {
     vector<Node *> vec;                                // 这里我们使用 STL 中的 vector 来代替数组，可利用到其动态扩展的属性
     vec.push_back(root);
     int cur = 0, last = 1;                             // vec.size(); 就像 iterator，指向 end
     while( cur < vec.size() ) {
          last = vec.size();                            // 新的一行访问开始，重新定位 last 于当前行最后一个节点的下一个位置
          while( cur < last ) {
               cout << vec[cur] -> data << " ";         // 访问节点
               if(vec[cur] -> lChild) { vec.push_back(vec[cur] -> lChild); }
               if(vec[cur] -> rChild) { vec.push_back(vec[cur] -> rChild); }
               ++cur;
          }
          cout << endl;                                 // 当 cur == last 时, 说明该层访问结束，输出换行符
     }
}

书中没有提及，本问题其实是以广度优先搜索 (breath-first search, BFS) 去遍历一个树结构。广度优先搜索的典型实现是使用队列 (queue)。其伪代码如下:

enqueue(Q, root)
do
    node = dequeue(Q)
    process(node)               // 如把内容列印
    for each child of node
        enqueue(Q, child)
while Q is not empty

书上的解法，事实上也使用了一个队列。但本人认为，使用 vector 容器，较不直觉，而且其空间复杂度是 O(n)。

如果用队列去实现 BFS，不处理换行，能简单翻译伪代码为 C++ 代码:

void PrintBFS(Node* root) {
    queue<Node*> Q;
    Q.push(root);
    do {
        Node *node = Q.front(); Q.pop();
        cout << node->data << " ";
        if (node->pLeft)  { Q.push(node->pLeft); }
        if (node->pRight) { Q.push(node->pRight); }
    }
    while (!Q.empty());
}

本人觉得这样的算法实现可能比较清楚，而且空间复杂度只需 O(m)，m 为树中最多节点的层的节点数量。最坏的情况是当二叉树为完整，m = n/2。之后的难点在于如何换行。

本人的尝试之一 @

第一个尝试，利用了两个队列，一个储存本层的节点，另一个储存下层的节点。遍历本层的节点，把其子代节点排入下层队列。本层遍历完毕后，就可换行，并交换两个队列。

void PrintNodeByLevel(Node* root) {
    deque<Node*> Q1, Q2;
    Q1.push_back(root);
    do {
        do {
            Node* node = Q1.front();
            Q1.pop_front();
            cout << node->data << " ";
            if (node->pLeft)
                Q2.push_back(node->pLeft);
            if (node->pRight)
                Q2.push_back(node->pRight);
        } while (!Q1.empty());
        cout << endl;
        Q1.swap(Q2);
    } while(!Q1.empty());
}

本实现使用 deque 而不是 queue，因为 deque 才支持 swap() 操作 ( swap(q1, q2) )。注意， swap() 是 O(1) 的操作，实际上只是交换指针。

这实现要用两个循环(书上的实现也是)，并且用了两个队列。能够只用一个循环、一个队列么?

本人的尝试之二

换行问题其实在于如何表达一层的结束。书上采用了游标，而第一个尝试则用了两个队列。本人想到第三个可行方案，是把一个结束信号放进队列里。由于使用 queue<Node*>，可以插入一个空指针去表示一层的遍历结束。

void PrintNodeByLevel(Node* root) {
    queue<Node*> Q;
    Q.push(root);
    Q.push(0);      // indicate end of level
    do {
        Node* node = Q.front(); Q.pop();
        if (node) {
            cout << node->data << " ";
            if ( node->pLeft  ) { Q.push(node->pLeft); }
            if ( node->pRight ) { Q.push(node->pRight); }
        } else if (!Q.empty()) {
            cout << endl;
            Q.push(0);
        }
    } while (!Q.empty());
}

这个实现的代码很贴近之前的 PrintBFS()，也只有一个循环。注意一点，当发现空指针 (结束信号) 时，要检查队列内是否还有节点，如果没有的话还插入新的结束信号，则会做成死循环。

测试代码 @

void Link(Node* nodes, int parent, int left, int right) {
    if (left != -1)
        nodes[parent].pLeft = &nodes[left];

    if (right != -1)
        nodes[parent].pRight = &nodes[right];
}

void main()
{
    Node test1 = { 0 };

    for (int i = 1; i < 9; i++)
        test1[i].data = i;

    Link(test1, 1, 2, 3);
    Link(test1, 2, 4, 5);
    Link(test1, 3, 6, -1);
    Link(test1, 5, 7, 8);

    PrintBFS(&test1);
    cout << endl << endl;

    PrintNodeByLevel(&test1);
    cout << endl;

面试题：检测点是否在扇形之内 - Milo Yip - 博客园
怎样判断平面上一个矩形和一个圆形是否有重叠？ - Milo Yip 的回答 - 知乎 @

最后要比较 u 和 r 的长度，若距离少于 r，则两者相交。可以只求 u 的长度平方是否小于 r 的平方。
两条像面试用的编程问题，和我的囧事 - Milo Yip - 博客园 @
- 设计一个函数 f，使得它满足：f(f(x))=-x，这里输入参数为 32 位整型
- 设计一个函数 g，满足：g(g(x))=1/x，x 是浮点数
今天午饭时间就发了以下的错误证明：
- 假设一个函数 f 存在，x 为 32-bit 整数，f(x)) = -x
- 设 y = f(x)
- f(f(x)) = -x -> f(y) = –x
- 变换变量, f(y) = -x -> f(x) = -y -> y = -f(x)
- y = f(x) = -f(x)
第 5 步只是当 y=0 才成立，和 f 的值域矛盾，按反证法，函数 f 不存在。

郑老师指出，只有自由变量 (Free Variable) 才可以置换 (Subsititue)。

这两问题的难点在于，函数不能储存额外状态。

我们首先分析问题 (1)，设 y=f(x)，则
- f(x) = y
- f(y) = -x
如果再把结果 -x 再应用一次 f 函数，f(-x) = ?

因为之前 f(y)=-x，而按题目定义，f(f(y))=-y ，所以 f(-x) = -y。我们可以列出:
- f(-x) = -y
- f(-y) = x
我们可以发现，4 次函数映射之后，会变成一个循环。也就是说，
```
x → y → –x → –y → x→ ...
```
我们只要把数字分为四类，就可以实现这个循环。x 和 -x 的分别是正负号，我们可以再利用数字的奇偶性，这两个正交属性可以产生 4 个组合。这个循环就可变成
```
正奇→ 正偶→ 负奇→ 负偶→ 正奇→ ...
```
郑老师说他经过几次推敲，得到:

f(x) = (-1)^xx + sign(x)
```
template<typename t>
inline T even(T x) {
    return x % 2 == 0 ? -1 : 1;
}

template<typename t>
inline T sgn(T x) {
    if (x > 0)
        return 1;
    else if (x < 0)
        return -1;
    else
        return 0;
}

template<typename t>
struct f1 {
    T operator()(T x) {
        return even(x) * x + sgn(x);
    }
};
```
```
#include <limits>
#include <iostream>

using namespace std;

template<typename T, typename F>
void test(F f) {
    cout << "[" << (int)numeric_limits<T>::min() << "," << (int)numeric_limits<T>::max() << "]" << endl;
    T x = numeric_limits<T>::min();
    do {
        T y = f(f(x));
        if (y != (T)-x)
            cout << (int)x << " " << (int)y << endl;
        x++;
    } while (x != numeric_limits<T>::min());

    cout << endl;
}

void main() {
    test<signed char>(f1<signed char>());
    test<signed short>(f1<signed short>());
    test<int>(f1<int>());

    test<signed char>(f2<signed char>());
    test<signed short>(f2<signed short>());
    test<int>(f2<int>());
}
```
```
[-128,127]
127 127

[-32768,32767]
32767 32767

[-2147483648,2147483647]
2147483647 2147483647
```
这结果说明，除了 x 为整数的上限时，结果正确。但因为没有额外的状态，相信这个边界问题应该不能解决。

第二题比较简单，只需要利用 -(-x) = x 的特点，无论 x 为正或负，经过这两次映射，总会有一次为正数，一次为负数。所以可以写一个函数，在 x 为正数时 (或负数时) 计算其倒数:
```
float g(float x) {
    return x > 0 ? -1.0f / x : -x;
}
```

LeetCode solutions | MaskRay ♥️ @

见 4ker/LeetCode。

read online: http://tangzx.qiniudn.com/notes/leetcode-maskray/index.html

refs and see also

LeetCode solutions | MaskRay

Add Two Numbers | LeetCode OJ @

Input: (2 -> 4 -> 3) + (5 -> 6 -> 4)
Output: 7 -> 0 -> 8

// 时间复杂度 O(m+n)，空间复杂度 O(1)
class Solution {
public:
    ListNode *addTwoNumbers(ListNode *l1, ListNode *l2) {
        ListNode dummy(-1);                                 // 头节点
        ListNode *prev = &dummy;
        int carry = 0;
        for (ListNode *pa = l1, *pb = l2;
             pa != nullptr || pb != nullptr;
             pa = pa == nullptr ? nullptr : pa->next,       // 这两个“下一步”不要太赞！
             pb = pb == nullptr ? nullptr : pb->next,
             prev = prev->next) {
            int ai = pa == nullptr ? 0 : pa->val;
            int bi = pb == nullptr ? 0 : pb->val;
            int value = (ai + bi + carry) % 10;
            carry = (ai + bi + carry) / 10;
            prev->next = new ListNode(value);               // 尾插法
        }
        if (carry > 0)
            prev->next = new ListNode(carry);
        return dummy.next;
    }
};

class Solution {
public:
    ListNode *addTwoNumbers(ListNode *l1, ListNode *l2) {
        ListNode *r = NULL, *p = NULL;
        int c = 0;
        while (l1 || l2) {
            if (l1) {
                c += l1->val;
                l1 = l1->next;
            }
            if (l2) {
                c += l2->val;
                l2 = l2->next;
            }
            auto x = new ListNode(c%10);
            c /= 10;
            if (! r)                    // 这里可以对比出上面的 dummy node 多么巧妙
                r = p = x;
            else {
                p->next = x;
                p = p->next;
            }
        }
        if (c)
            p->next = new ListNode(c);
        return r;
    }
};

一个类似的题：

Add Binary | LeetCode OJ @

// 时间复杂度 O(n)，空间复杂度 O(1)
class Solution {
public:
    string addBinary(string a, string b) {
        const size_t n = max( a.size(), b.size() );
        string result;
        result.reserve( n+1 );
        result.resize( n );
        reverse(a.begin(), a.end());
        reverse(b.begin(), b.end());
        int carry = 0;
        for (size_t i = 0; i < n; i++) {
            int ai = i < a.size() ? a[i] - '0' : 0;
            int bi = i < b.size() ? b[i] - '0' : 0;
            int val = (ai + bi + carry) % 2;
            carry = (ai + bi + carry) / 2;
            result[i] = val + '0';
        }
        if (carry == 1) {
            result.push_back( '1' );
        }
        reverse( result.begin(), result.end() );
        return result;
    }
};

还有一个类似的题，这个可以提前退出（因为不是两个数相加）：

Plus One | LeetCode OJ @

这个直观：

class Solution {
public:
    vector<int> plusOne(vector<int> &digits) {
        add(digits, 1);
        return digits;
    }
private:
    // 0 <= digit <= 9
    void add(vector<int> &digits, int digit) {
        int c = digit;  // carry, 进位

        for (auto it = digits.rbegin(); it != digits.rend(); ++it) {
            *it += c;
            c = *it / 10;
            *it %= 10;
            if( !c ) { return; } // 没有 carry 就退出咯
        }

        if (c > 0) digits.insert(digits.begin(), 1);
    }
};

这个不太好理解：

class Solution {
public:
    vector<int> plusOne(vector<int> &a) {
        using namespace std::placeholders;
        if (find_if(a.begin(), a.end(), bind(not_equal_to<int>(), _1, 9)) == a.end()) {
            a.assign(a.size()+1, 0);
            a[0] = 1;
        } else {
            int i = a.size();
            while (++a[--i] >= 10)
                a[i] -= 10;
        }
        return a;
    }
};

Reverse Linked List | LeetCode OJ ♥️ @

class Solution {
public:
    ListNode* reverseList(ListNode* x) {
        ListNode *y = 0, *t;    // 初始为 0
        while (x) {
            t = x->next;        // 保存后面可以执行的内容
            x->next = y;        // 颠倒方向，指向上一个头指针
            y = x;              // 更新头指针
            x = t;              // 下一步
        }
        return y;
    }
};

Reverse Linked List II | LeetCode OJ ♥️ ♥️ @

难在需要在指定范围内 reverse。

已经保证了：1 ≤ m ≤ n ≤ length of list。

Reverse a linked list from position m to n. Do it in-place and in one-pass.

For example:

Given 1->2->3->4->5->NULL, m = 2 and n = 4,
return 1->4->3->2->5->NULL.

初始：
    1   ->  2   ->  3   ->  4   ->  5   ->  NULL

操作：
        +-------------------+
        |                   |
        |                   V
    1 ->+   2   <-  3   <-  4       5   ->  NULL
            |                       ^
            |                       |
            +-----------------------+

结果：
    1   ->  4   ->  3   ->  2   ->  5   ->  NULL

dummy.next = &1
prev = &dummy

    1   ->  2   ->  3   ->  4   ->  5   ->  NULL
    ^
    |
    prev, head2


            +-----------------------+
            |                       |
            |                       V
    1   ->  2   ->  3   ->  4   ->  5   ->  NULL
    ^       ^       ^       ^
    |       |       |       |
    head2   prev <- cur     |
            |               |
            +---------------+

// 迭代版，时间复杂度 O(n)，空间复杂度 O(1)
class Solution {
public:
    ListNode *reverseBetween(ListNode *head, int m, int n) {
        ListNode dummy(-1);
        dummy.next = head;

        ListNode *prev = &dummy;
        for (int i = 0; i < m-1; ++i)
            prev = prev->next;

        ListNode *head2 = prev;                 // head2 指向变化区域之前的一个元素
        prev            = head2->next;
        ListNode *cur   = prev->next;
        for (int i = m; i < n; ++i) {
            prev->next = cur->next;             // 保存
            cur->next = head2->next;            // 这是保存了的”新“头，也就是上一个节点，第一次调用的时候，恰好是 &5
            head2->next = cur;                  // 头插法
            cur = prev->next;                   // 恢复
        }

        return dummy.next;
    }
};

LRU Cache | LeetCode OJ @

Design and implement a data structure for Least Recently Used (LRU) cache. It should support the following operations: get and set.

get(key) - Get the value (will always be positive) of the key if the key exists in the cache, otherwise return -1.

set(key, value) - Set or insert the value if the key is not already present. When the cache reached its capacity, it should invalidate the least recently used item before inserting a new item.

为了使查找、插入和删除都有较高的性能，我们使用一个双向链表 (std::list) 和一个哈希表 (std::unordered_map)，因为：

哈希表保存每个节点的地址，可以基本保证在 O(1) 时间内查找节点
双向链表插入和删除效率高，单向链表插入和删除时，还要查找节点的前驱节点

具体实现细节：

越靠近链表头部，表示节点上次访问距离现在时间最短，尾部的节点表示最近访问最少}
访问节点时，如果节点存在，把该节点交换到链表头部，同时更新 hash 表中该节点的地址}
插入节点时，如果 cache 的 size 达到了上限 capacity，则删除尾部节点，同时要在 hash 表中删除对应的项；新节点插入链表头部}

class LRUCache {
public:
    LRUCache(int capacity) : c(capacity) {}

    void touch(int key) {
        pair<int, int> x = *s[key];
        a.erase(s[key]);
        a.push_front(x);
        s[x.first] = a.begin();
    }

    int get(int key) {
        if (! s.count(key))
            return -1;
        touch(key);
        return a.begin()->second;
    }

    void set(int key, int value) {
        if (s.count(key)) {
            touch(key);
            a.begin()->second = value;
        } else {
            if (s.size() >= c) {
                s.erase(a.rbegin()->first);
                a.pop_back();
            }
            a.push_front(make_pair(key, value));
            s[key] = a.begin();
        }
    }

private:
    map<int, list<pair<int, int> >::iterator> s;
    list<pair<int, int> > a;
    int c;
};

Valid Palindrome | LeetCode OJ @

这个很巧妙，移动到左侧。

class Solution {
public:
    bool isPalindrome(string s) {
        int i = 0, j = 0;
        for (; i < s.size(); i++)
            if (isalnum(s[i]))
                s[j++] = s[i];
        for (i = 0; i < --j; i++)
            if (tolower(s[i]) != tolower(s[j]))
                return false;
        return true;
    }
};

这个不会修改 s（虽然是一个拷贝，无所谓修改）

class Solution {
public:
    bool isPalindrome(string s) {
        int left = 0, right = s.size()-1;
        while( left < right ) {
            while( !::isalnum(s[left])  && left+1 <= right ) { ++left;  }
            while( !::isalnum(s[right]) && right-1 >= left ) { --right; }
            if( left < right ) {
                if( ::tolower(s[left]) != ::tolower(s[right]) ) {
                    return false;
                }
            }
            ++left;
            --right;
        }
        return true;
    }
};

Longest Palindromic Substring | LeetCode OJ ♥️ @

先理解下啥是 Longest substring @

Nil.

refs and see also

Longest common substring problem - Wikipedia, the free encyclopedia

Difficulty: Medium

Given a string S, find the longest palindromic substring in S. You may assume that the maximum length of S is 1000, and there exists one unique longest palindromic substring.

思路一：暴力枚举，以每个元素为中间元素，同时从左右出发，复杂度 O(n^2) @

这个效率并不低。

思路二：记忆化搜索，复杂度 O(n^2)。设 f[i][j] 表示 [i,j] 之间的最长回文子串 @

递推方程如下：

f[i][j] = if (i == j) S[i]
          if (S[i] == S[j] && f[i+1][j-1] == S[i+1][j-1]) S[i][j]
          else max(f[i+1][j-1], f[i][j-1], f[i+1][j])

// 时间复杂度 O(n^2)，空间复杂度 O(n^2)
typedef string::const_iterator Iterator;

namespace std {
template<>
struct hash<pair<Iterator, Iterator>> {
    size_t operator()(pair<Iterator, Iterator> const& p) const {
        return ((size_t) &(*p.first)) ^ ((size_t) &(*p.second));
    }
};
}

class Solution {
public:
    string longestPalindrome(string const& s) {
        cache.clear();
        return cachedLongestPalindrome(s.begin(), s.end());
    }

private:
    unordered_map<pair<Iterator, Iterator>, string> cache;

    string longestPalindrome(Iterator first, Iterator last) {
        size_t length = distance(first, last);

        if (length < 2) return string(first, last);

        auto s = cachedLongestPalindrome(next(first), prev(last));

        if (s.length() == length - 2 && *first == *prev(last))
            return string(first, last);

        auto s1 = cachedLongestPalindrome(next(first), last);
        auto s2 = cachedLongestPalindrome(first, prev(last));

        // return max(s, s1, s2)
        if (s.size() > s1.size()) return s.size() > s2.size() ? s : s2;
        else return s1.size() > s2.size() ? s1 : s2;
    }

    string cachedLongestPalindrome(Iterator first, Iterator last) {
        auto key = make_pair(first, last);
        auto pos = cache.find(key);

        if (pos != cache.end()) return pos->second;
        else return cache[key] = longestPalindrome(first, last);
    }
};

思路三：动规，复杂度 O(n^2)。设状态为 f(i,j)，表示区间 [i,j] 是否为回文串 @

则状态转移方程为

                    true                                        i=j
f(i,j)      =       S[i]=S[j]                                   j = i + 1
                    S[i]=S[j] and f(i+1, j-1)                   j > i + 1

// 动规，时间复杂度 O(n^2)，空间复杂度 O(n^2)
class Solution {
public:
    string longestPalindrome(const string& s) {
        const int n = s.size();
        bool f[n][n];
        fill_n(&f[0][0], n * n, false);
        size_t max_len = 1, start = 0;  // 最长回文子串的长度，起点

        for (size_t i = 0; i < s.size(); i++) {
            f[i][i] = true;
            for (size_t j = 0; j < i; j++) {            // 区间：[j, i]
                // 这个 f[j+1][i-1] 决定了 i 的遍历顺序，j 无所谓，因为上一层的都是计算过的
                f[j][i] = ( s[j] == s[i] && (i - j < 2 || f[j + 1][i - 1]) );
                if (f[j][i] && max_len < (i - j + 1)) {
                    max_len = i - j + 1;
                    start = j;
                }
            }
        }
        return s.substr(start, max_len);
    }
};

Soulmachine 说用 vector 会超时 vector<vector<bool> > f(n, vector<bool>(n, false));，估计是 vector<bool> 寻址效率太低导致。其实换成 vector<vector<int>> f 就好了。

思路四：Manacher’s Algorithm, 复杂度 O(n)。 @

详细见 Longest Palindromic Substring Part II – LeetCode。（下文有摘录。）

// Longest Palindromic Substring
// Manacher's algorithm

#define FOR(i, a, b) for (decltype(b) i = (a); i < (b); i++)
#define REP(i, n) FOR(i, 0, n)

class Solution {
public:
    string longestPalindrome(string s) {
        string a(2*s.size()+1, '.');
        vector<int> z(2*s.size()+1);
        REP(i, s.size())
            a[2*i+1] = s[i];
        for (int f, g = 0, i = 0; i < a.size(); i++)
            if (i < g && z[2*f-i] != g-i)
                z[i] = min(z[2*f-i], g-i);
            else {
                f = i;
                g = max(g, i);
                while (g < a.size() && 2*f-g >= 0 && a[g] == a[2*f-g]) g++;
                z[i] = g-f;
            }
        int x = max_element(z.begin(), z.end()) - z.begin();
        return s.substr((x-z[x]+1)/2, z[x]-1);
    }
};

LeetCode 上面的分析也挺有意思 @

Stated more formally below:
    Define P[ i, j ] ← true iff the substring Si … Sj is a palindrome, otherwise false.

Therefore,
    P[ i, j ] ← ( P[ i+1, j-1 ] and Si = Sj )

The base cases are:
    P[ i, i ] ← true
    P[ i, i+1 ] ← ( Si = Si+1 )

This yields a straight forward DP solution, which we first initialize the one and two letters palindromes, and work our way up finding all three letters palindromes, and so on…

This gives us a run time complexity of O(N2) and uses O(N2) space to store the table.

string longestPalindromeDP(string s) {
    int n = s.length();
    int longestBegin = 0;
    int maxLen = 1;
    bool table[1000][1000] = {false};
    for (int i = 0; i < n; i++) {
        table[i][i] = true;
    }
    for (int i = 0; i < n-1; i++) {
        if (s[i] == s[i+1]) {
            table[i][i+1] = true;
            longestBegin = i;
            maxLen = 2;
        }
    }
    for (int len = 3; len <= n; len++) {
        for (int i = 0; i < n-len+1; i++) {
            int j = i+len-1;
            if (s[i] == s[j] && table[i+1][j-1]) {
                table[i][j] = true;
                longestBegin = i;
                maxLen = len;
            }
        }
    }
    return s.substr(longestBegin, maxLen);
}

或者，从中心像两边扩张。

string expandAroundCenter(string s, int c1, int c2) {
    int l = c1, r = c2;
    int n = s.length();
    while (l >= 0 && r <= n-1 && s[l] == s[r]) {
        l--;
        r++;
    }
    return s.substr(l+1, r-l-1);
}

string longestPalindromeSimple(string s) {
    int n = s.length();
    if (n == 0) return "";
    string longest = s.substr(0, 1);  // a single char itself is a palindrome
    for (int i = 0; i < n-1; i++) {
        string p1 = expandAroundCenter(s, i, i);
        if (p1.length() > longest.length())
            longest = p1;

        string p2 = expandAroundCenter(s, i, i+1);
        if (p2.length() > longest.length())
            longest = p2;
    }
    return longest;
}

An O(N) Solution (Manacher’s Algorithm)，TODO

refs and see also

Longest Palindromic Substring Part II – LeetCode

Regular Expression Matching | LeetCode OJ @

// 递归版，时间复杂度 O(n)，空间复杂度 O(1)

class Solution {
public:
    bool isMatch(const string& s, const string& p) {
        return isMatch(s.c_str(), p.c_str());
    }
private:
    bool isMatch(const char *s, const char *p) {
        if ( *p == '\0' ) { return *s == '\0'; }

        // next char is not '*', then must match current character
        if (*(p + 1) != '*') {
            if (*p == *s || (*p == '.' && *s != '\0'))
                return isMatch(s + 1, p + 1);
            else
                return false;
        } else { // next char is '*'
            while (*p == *s || (*p == '.' && *s != '\0')) {
                if (isMatch(s, p + 2))
                    return true;
                s++;
            }
            return isMatch(s, p + 2);
        }
    }
};

// Regular Expression Matching
#define REP(i, n) for (int i = 0; i < (n); i++)

class Solution {
private:
    struct State {
        int c;
        bool epsf, epsb;
        State() : c(-2), epsf(false), epsb(false) {}
    };
public:
    bool isMatch(const char *s, const char *p) {
        vector<State> states(1);
        while (*p) {
            states.back().c = *p == '.' ? -1 : *p;
            states.emplace_back();
            if (*++p == '*') {
                states.back().epsb = true;
                states[states.size()-2].epsf = true;
                p++;
            }
        }

        vector<bool> f(states.size()), ff(states.size());
        f[0] = true;
        for (;; s++) {
            REP(i, states.size())
                if (f[i]) {
                    if (states[i].epsf)
                        f[i+1] = true;
                    if (states[i].epsb)
                        f[i-1] = true;
                }
            if (! *s) break;
            fill(ff.begin(), ff.end(), false);
            REP(i, states.size())
                if (f[i] && (states[i].c == -1 || states[i].c == *s))
                    ff[i+1] = true;
            f.swap(ff);
        }
        return f.back();
    }
};

compile error.

Longest Common Prefix | LeetCode OJ @

复杂度都是 O(n1+n2+…)

纵向扫描。

// Longest Common Prefix
#define FOR(i, a, b) for (decltype(b) i = (a); i < (b); i++)
#define REP(i, n) FOR(i, 0, n)

class Solution {
public:
    string longestCommonPrefix(vector<string> &strs) {
        if (strs.empty()) return "";
        int r = 0;
        for(;;) {
            char c = strs[0][r];
            REP(i, strs.size())
                if (! strs[i][r] || strs[i][r] != c)
                    return strs[0].substr(0, r);
            r++;
        }
    }
};

或者，横向扫描。

// 横向扫描，每个字符串与第 0 个字符串，从左到右比较，直到遇到一个不匹配，然后继续下一个字符串
class Solution {
public:
    string longestCommonPrefix(vector<string> &strs) {
        if (strs.empty()) return "";
        int right_most = strs[0].size() - 1;
        for (size_t i = 1; i < strs.size(); i++)
            for (int j = 0; j <= right_most; j++)
                if (strs[i][j] != strs[0][j])                   // 不会越界，请参考string::[]的文档
                    right_most = j - 1;

        return strs[0].substr(0, right_most + 1);
    }
};

// Valid Parentheses
class Solution {
public:
    bool isValid(string s) {
        stack<char> st;
        char cc;
        for (auto c: s)
            switch (c) {
            case '(': case '[': case '{':
                st.push(c);
                break;
            case ')': case ']': case '}':
                if (st.empty() || (cc = st.top(), st.pop(), cc+1 != c && cc+2 != c))
                    return false;
            }
        return st.empty();
    }
};

Recover Binary Search Tree | LeetCode OJ @

Two elements of a binary search tree (BST) are swapped by mistake.

Recover the tree without changing its structure.

Note:

A solution using O(n) space is pretty straight forward. Could you devise ([dɪ'vaɪz]，想出) a constant space solution?

O(n) 空间的解法是，开一个指针数组，中序遍历，将节点指针依次存放到数组里，然后寻找两处逆向的位置，先从前往后找第一个逆序的位置，然后从后往前找第二个逆序的位置，交换这两个指针的值。

中序遍历一般需要用到栈，空间也是 O(n) 的，如何才能不使用栈？Morris 中序遍历。

// Recover Binary Search Tree
// Morris in-order traversal

class Solution {
public:
    void recoverTree(TreeNode *p) {
        TreeNode *u = NULL, *v, *l= NULL;
        while (p) {
            TreeNode *q = p->left;
            if (q) {
                while (q->right && q->right != p)
                    q = q->right;
                if (! q->right) {
                    q->right = p;
                    p = p->left;
                    continue;
                }
                q->right = NULL;
            }
            if (l && l->val > p->val)
                if (! u)
                    u = l, v = p;
                else
                    v = p;
            l = p;
            p = p->right;
        }
        swap(u->val, v->val);
    }
};

Same Tree | LeetCode OJ @

class Solution {
public:
    bool isSameTree(TreeNode *p, TreeNode *q) {
        if (!p && !q) return true;
        if (!p || !q) return false;
        return p->val == q->val && isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
    }
};

迭代？那就用 stack，先 push 两个指针，然后每次取出两个，进行比较。

Flatten Binary Tree to Linked List | LeetCode OJ @

// Flatten Binary Tree to Linked List
class Solution {
public:
    void flatten(TreeNode *root) {
        for (; root; root = root->right)
            if (root->left) {
                TreeNode *x = root->left;
                while (x->right) x = x->right;      // 找到衔接点
                x->right = root->right;             // 把 root 粘贴过来
                root->right = root->left;           // 左侧放到右侧
                root->left = NULL;                  // 左侧置空
            }
    }
};

Minimum Depth of Binary Tree | LeetCode OJ @

// 递归版，时间复杂度O(n)，空间复杂度O(logn)
class Solution {
public:
    int minDepth(const TreeNode *root) {
        return minDepth(root, false);
    }
private:
    static int minDepth(const TreeNode *root, bool hasbrother) {
        if (!root) return hasbrother ? INT_MAX : 0;

        return 1 + min( minDepth(root->left, root->right ),
                        minDepth(root->right, root->left ) );
    }
};

我没有看懂的迭代版：

// 迭代版，时间复杂度 O(n)，空间复杂度 O(logn)
class Solution {
public:
    int minDepth(TreeNode* root) {
        if ( !root ) { return 0; }

        int result = INT_MAX;

        stack<pair<TreeNode*, int>> s;
        s.push(make_pair(root, 1));

        while (!s.empty()) {
            auto node = s.top().first;
            auto depth = s.top().second;
            s.pop();

            if (node->left == nullptr && node->right == nullptr)
                result = min(result, depth);

            if (node->left && result > depth) // 深度控制，剪枝
                s.push(make_pair(node->left, depth + 1));

            if (node->right && result > depth) // 深度控制，剪枝
                s.push(make_pair(node->right, depth + 1));
        }

        return result;
    }
};

Maximum Depth of Binary Tree | LeetCode OJ @

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if( !root ) { return 0; }
        return max( maxDepth(root->left), maxDepth(root->right) ) + 1;
    }
};

Path Sum | LeetCode OJ @

// 时间复杂度 O(n)，空间复杂度 O(logn)
class Solution {
public:
    bool hasPathSum(TreeNode *root, int sum) {
        if ( !root ) { return false; }                              // 目标还没完成，就没路了。

        if ( !root->left && !root->right ) {                        // 最后一次机会
            return sum == root->val;
        }

        return hasPathSum(  root->left, sum - root->val ) ||        // 交给下面的人来处理
               hasPathSum( root->right, sum - root->val );
    }
};

Path Sum II | LeetCode OJ @

// 时间复杂度 O(n)，空间复杂度 O(logn)
class Solution {
public:
    vector<vector<int> > pathSum(TreeNode *root, int sum) {
        vector<vector<int> > result;
        vector<int> cur;                                                // 中间结果
        pathSum(root, sum, cur, result);
        return result;
    }
private:
    void pathSum(TreeNode *root, int gap, vector<int> &cur, vector<vector<int> > &result) {
        if ( !root ) { return; }
        cur.push_back( root->val );
        if ( !root->left && !root->right && root->val == gap ) {
            result.push_back( cur );                            // 不可 return！！
        }
        pathSum( root->left,  gap - root->val, cur, result );   // 进去后会还原 cur
        pathSum( root->right, gap - root->val, cur, result );   // 所以不懂担心上面的处理会影响到这里
        cur.pop_back();
    }
};

这里的 cur.pop_back() 是必须的，除非你更改函数签名：

void pathSum(TreeNode *root, int gap, vector<int> cur, vector<vector<int> > &result) {

Merge Sorted Array | LeetCode OJ @

我的方法：

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        vector<int> result(m+n);
        int i = 0, j = 0, k = 0;
        while( i < m && j < n ) {
            if ( nums1[i] < nums2[j] ) {
                result[k++] = nums1[i++];
            } else {
                result[k++] = nums2[j++];
            }
        }
        while( i < m ) { result[k++] = nums1[i++]; }
        while( j < n ) { result[k++] = nums2[j++]; }
        nums1.swap( result );
    }
};

Maskray 的：（没有用额外的空间！）

class Solution {
public:
    void merge(vector<int> &a, int m, vector<int> &b, int n) {
        vector<int> c(m+n);
        for (int i = 0, j = 0; i < m || j < n; )
            if (j == n || i < m && a[i] < b[j]) {
                c[i+j] = a[i];
                ++i;
            } else {
                c[i+j] = b[j];
                ++j;
            }
        a.swap(c);
    }
};

Soulmachine 的：

// 时间复杂度 O(m+n)，空间复杂度 O(1)
class Solution {
public:
    void merge(vector<int>& A, int m, vector<int>& B, int n) {
        int ia = m - 1, ib = n - 1, icur = m + n - 1;
        while(ia >= 0 && ib >= 0) {
            A[icur--] = A[ia] >= B[ib] ? A[ia--] : B[ib--];
        }
        while(ib >= 0) {
            A[icur--] = B[ib--];
        }
    }
};

Merge Two Sorted Lists | LeetCode OJ @

// 时间复杂度 O(min(m,n))，空间复杂度 O(1)
class Solution {
public:
    ListNode *mergeTwoLists(ListNode *l1, ListNode *l2) {
        if ( !l1 ) { return l2; }
        if ( !l2 ) { return l1; }
        ListNode dummy(-1);
        ListNode *p = &dummy;
        for ( ; l1 && l2; p = p->next) {        // 还有节点可以拼接
            if ( l1->val < l2->val ) {
                p->next = l1;
                l1 = l1->next;
            } else {
                p->next = l2;
                l2 = l2->next;
            }
        }
        p->next = l1 ? l1 : l2;                 // 哪边还剩下？
        return dummy.next;
    }
};

First Missing Positive | LeetCode OJ @

Given an unsorted integer array, find the first missing positive integer.

For example,
Given [1,2,0] return 3,
and [3,4,-1,1] return 2.

Your algorithm should run in O(n) time and uses constant space.

本质上是桶排序(bucket sort)，每当 A[i]!= i+1 的时候，将 A[i] 与 A[A[i]-1] 交换，直到无法交换为止，终止条件是 A[i]== A[A[i]-1]。

// First Missing Positive
#define REP(i, n) for (int i = 0; i < (n); i++)
class Solution {
public:
    int firstMissingPositive(vector<int> &a) {
        int n = a.size();
        REP(i, n)
            while (0 < a[i] && a[i] <= n && a[a[i]-1] != a[i])  // a[i] 的位置不对
                swap(a[a[i]-1], a[i]);                          // 那我们把它放到正确的位置 a[i]-1
        REP(i, n)
            if (a[i] != i+1)
                return i+1;
        return n+1;
    }
};

其实所有的逻辑只是：

1 <= a[i] <= n 的位置有没有正确摆放？（应该放在 a[i]-1 的位置）
没有正确摆放的话（a[i] != a[a[i]-1]），那就放到正确的位置：swap(a[a[i]-1], a[i])
这样之后，总还有元素没有正确被摆放
1. 可能是被抢了位置
2. 也可能是他们不在 1 <= n 的范围内

1   2   0
置换
1   2   0
看是否匹配
1   2   ?
        ^ 失配

3   4  -1   1
置换
-1  4   3   1
-1  1   3   4
-1  1   3   4
看是否匹配
-1  1   3   4
^ 失配

1   3   5   4
1   5   3   4
    ^

2   4   3   6   5   7
4   2   3   7   5   6
^

Sort Colors | LeetCode OJ @

Given an array with n objects colored red, white or blue, sort them so that objects of the same color are adjacent, with the colors in the order red, white and blue.

Here, we will use the integers 0, 1, and 2 to represent the color red, white, and blue respectively.

Note:

You are not suppose to use the library’s sort function for this problem.

如此简单，就是一个计数排序（counting sort），而已。

A rather straight forward solution is a two-pass algorithm using counting sort.

First, iterate the array counting number of 0’s, 1’s, and 2’s, then overwrite array with total number of 0’s, then 1’s and followed by 2’s.

class Solution {
public:
    void sortColors(vector<int> &a) {
        int c[3] = {};
        for (auto x: a)
            c[x]++;
        fill_n(a.begin(), c[0], 0);             //  for (int i = 0, index = 0; i < 3; i++)
        fill_n(a.begin()+c[0], c[1], 1);        //      for (int j = 0; j < counts[i]; j++)
        fill_n(a.begin()+c[0]+c[1], c[2], 2);   //          A[index++] = i;
    }
};

Follow up:

Could you come up with an one-pass algorithm using only constant space?

用 partition 的方法：

// red, white, blue
class Solution {
public:
    void sortColors(vector<int> &a) {
        for (int r = 0, w = 0, b = a.size(); w < b; )
            if (a[w] == 0)
                swap(a[r++], a[w++]);
            else if (a[w] == 2)
                swap(a[--b], a[w]);
            else
                w++;
    }
};

Search for a Range | LeetCode OJ @

// Search for a Range
class Solution {
public:
    vector<int> searchRange(vector<int> &a, int target) {
        int l = 0, m = a.size(), h = a.size();
        while (l < m) {
            int x = l+m >> 1;
            if (a[x] < target) l = x+1;
            else m = x;
        }
        vector<int> r;
        if (l == a.size() || a[l] != target) {
            r.push_back(-1);
            r.push_back(-1);
        } else {
            while (m < h) {
                int x = m+h >> 1;
                if (a[x] <= target) m = x+1;
                else h = x;
            }
            r.push_back(l);
            r.push_back(m-1);
        }
        return r;
    }
};

用 STL：

// 时间复杂度 O(logn)，空间复杂度 O(1)
class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        const int l = distance(nums.begin(), lower_bound(nums.begin(), nums.end(), target));
        const int u = distance(nums.begin(), prev(upper_bound(nums.begin(), nums.end(), target)));
        if (nums[l] != target) // not found
            return vector<int> { -1, -1 };
        else
            return vector<int> { l, u };
    }
};

Search a 2D Matrix | LeetCode OJ @

class Solution {
public:
    bool searchMatrix(vector<vector<int> > &a, int b) {
        int m = a.size(), n = a[0].size(), l = 0, h = m*n-1;
        while (l <= h) {
            int m = l+h >> 1;
            int &bb = a[m/n][m%n];
            if (bb < b) {
                l = m+1;
            } else if (bb > b){
                h = m-1;
            } else {
                return true;
            }
        }
        return false;
    }
};

class Solution {
public:
    bool searchMatrix(vector<vector<int> > &a, int b) {
        int m = a.size(), n = a[0].size(), l = 0, h = m*n;
        while (l < h) {
            int m = l+h >> 1;
            if (a[m/n][m%n] < b) {
                l = m+1;
            } else {
                h = m;
            }
        }
        return l < m*n && a[l/n][l%n] == b;
    }
};

Word Ladder | LeetCode OJ @

Given two words (beginWord and endWord), and a dictionary’s word list, find the length of shortest transformation sequence from beginWord to endWord, such that:

Only one letter can be changed at a time
Each intermediate word must exist in the word list

For example,

Given:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

As one shortest transformation is “hit” -> “hot” -> “dot” -> “dog” -> “cog”, return its length 5.

Note:

Return 0 if there is no such transformation sequence.
All words have the same length.
All words contain only lowercase alphabetic characters.

用单队列、双队列。

// Word Ladder
#define FOR(i, a, b) for (int i = (a); i < (b); i++)
#define REP(i, n) for (int i = 0; i < (n); i++)

class Solution {
public:
    int ladderLength(string start, string end, unordered_set<string> &dict) {
        unordered_map<string, int> d;
        queue<string> q;
        d[start] = 0;
        dict.insert(end);
        for (q.push(start); ! q.empty(); ) {
            string i = q.front();
            int dd = d[i];
            q.pop();
            REP(j, i.size()) {
                char cc = i[j];
                FOR(c, 'a', 'z'+1) {
                    i[j] = c;
                    if (dict.count(i)) {
                        dict.erase(i);
                        q.push(i);
                        d[i] = dd+1;
                    }
                }
                i[j] = cc;
            }
        }
        return d.count(end) ? d[end]+1 : 0;
    }
};

/// hamming distance trick

class Solution {
    bool hamming_one(const string &a, const string &b) {
        int i = 0, j = a.size();
        while (i < j && a[i] == b[i]) i++;
        while (i < j && a[j-1] == b[j-1]) j--;
        return i == j-1;
    }
public:
    int ladderLength(string start, string end, unordered_set<string> &dict) {
        unordered_map<string, int> d;
        unordered_map<string, vector<string>> left, right;
        queue<string> q;
        d[start] = 0;
        dict.erase(start);
        dict.insert(end);
        int n = start.length();
        for (auto &x: dict) {
            string l = x.substr(0, n/2), r = x.substr(n/2);
            left[l].push_back(r);
            right[r].push_back(l);
        }
        for (q.push(start); ! q.empty(); ) {
            string x = q.front(), l = x.substr(0, n/2), r = x.substr(n/2);
            int dd = d[x];
            q.pop();
            if (left.count(l))
                for (auto &y: left[l])
                    if (hamming_one(r, y)) {
                        string z = l+y;
                        if (dict.count(z)) {
                            dict.erase(z);
                            q.push(z);
                            d[z] = dd+1;
                        }
                    }
            if (right.count(r))
                for (auto &y: right[r])
                    if (hamming_one(l, y)) {
                        string z = y+r;
                        if (dict.count(z)) {
                            dict.erase(z);
                            q.push(z);
                            d[z] = dd+1;
                        }
                    }
        }
        return d.count(end) ? d[end]+1 : 0;
    }
};

/// bidirectional BFS + hamming distance trick

class Solution {
    bool hamming_one(const string &a, const string &b) {
        int i = 0, j = a.size();
        while (i < j && a[i] == b[i]) i++;
        while (i < j && a[j-1] == b[j-1]) j--;
        return i == j-1;
    }
public:
    int ladderLength(string start, string end, unordered_set<string> &dict) {
        unordered_map<string, vector<string>> left, right;
        int n = start.length(), d = 1;
        dict.insert(start);
        dict.insert(end);
        for (auto &x: dict) {
            string l = x.substr(0, n/2), r = x.substr(n/2);
            left[l].push_back(r);
            right[r].push_back(l);
        }
        dict.erase(start);
        dict.erase(end);
        unordered_set<string> q0{start}, q1{end};
        while (! q0.empty()) {
            if (q0.size() > q1.size()) {
                swap(q0, q1);
                continue;
            }
            d++;
            unordered_set<string> next;
            for (auto &x: q0) {
                string l = x.substr(0, n/2), r = x.substr(n/2);
                if (left.count(l))
                    for (auto &y: left[l])
                        if (hamming_one(r, y)) {
                            string z = l+y;
                            if (q1.count(z))
                                return d;
                            if (dict.count(z)) {
                                dict.erase(z);
                                next.insert(z);
                            }
                        }
                if (right.count(r))
                    for (auto &y: right[r])
                        if (hamming_one(l, y)) {
                            string z = y+r;
                            if (q1.count(z))
                                return d;
                            if (dict.count(z)) {
                                dict.erase(z);
                                next.insert(z);
                            }
                        }
            }
            q0.swap(next);
            q0.swap(q1);
        }
        return 0;
    }
};

Word Ladder II | LeetCode OJ @

用单队列、双队列，或者图的广搜。

Jump Game | LeetCode OJ @

Given an array of non-negative integers, you are initially positioned at the first index of the array.

Each element in the array represents your maximum jump length at that position.

Determine if you are able to reach the last index.

For example:

A = [2,3,1,1,4], return true.
A = [3,2,1,0,4], return false.

Edit Distance | LeetCode OJ @

Given two words word1 and word2, find the minimum number of steps required to convert word1 to word2. (each operation is counted as 1 step.)

You have the following 3 operations permitted on a word:

1. Insert a character
1. Delete a character
1. Replace a character

#define REP(i, n) for (int i = 0; i < (n); i++)

class Solution {
public:
    int minDistance(string a, string b) {
        vector<vector<int>> f(2, vector<int>(b.size()+1));
        iota(f[0].begin(), f[0].end(), 0);
        REP(i, a.size()) {
            f[i+1&1][0] = i+1;
            REP(j, b.size())
                f[i+1&1][j+1] = a[i] == b[j] ? f[i&1][j] : min(min(f[i&1][j], f[i&1][j+1]), f[i+1&1][j]) + 1;
        }
        return f[a.size()&1][b.size()];
    }
};

Finals @

面试必会内容之——操作系统 ♥️ @

refs and see also

面试必会内容之——操作系统 - 671coder的专栏 - 博客频道 - CSDN.NET

nonstriater/Learn-Algorithms: 算法学习笔记 ♥️ @

二叉查找树 @

二叉查找树（Binary search tree），也叫有序二叉树 (Ordered binary tree), 排序二叉树 (Sorted binary tree)。是指一个空树或者具有下列性质的二叉树：

若任意节点的左子树不为空，则左子树上所有的节点值小于它的根节点值
若任意节点的右子树不为空，则右子树上所有节点的值均大于它的根节点的值
任意节点左右子树也为二叉查找树
没有键值相等的节点

删除节点,需要重建排序树

删除节点是叶子节点（分支为0），结构不破坏
删除节点只有一个分支(分支为1)，结构也不破坏
删除节点有2个分支，此时删除节点
- 思路一：选左子树的最大节点，或右子树最小节点替换

伸展树 (splay tree) @

伸展树是一种自平衡的二叉排序树。为什么需要这些自平衡的二叉排序树？

n 个节点的完全二叉树，其查找，删除的复杂度都是 O(logN), 但是如果频繁的插入删除，导致二叉树退化成一个 n 个节点的单链表，也就是插入，查找复杂度趋于 O(N)，为了克服这个缺点，出现了很多二叉查找树的变形，如 AVL 树，红黑树，以及接下来介绍的伸展树 (splay tree)。

B 树 @

平衡查找树，一种多路查找树。

能保证数据插入和删除情况下，任然保持执行效率。

一个 M 阶的 B 树满足：

每个节点最多 M 个子节点
除跟节点和叶节点外，其它每个节点至少有 M/2 个孩子
根节点至少 2 个节点
所有叶节点在同一层，叶节点不包含任何关键字信息
有 k 个关键字的页节点包含 k+1 个孩子

也就是说：根节点到每个叶节点的路径长度都是相同的。

B+ 树 @

mysql 索引使用 B+ 树的数据结构

赫夫曼编码 Huffman @

这是一个经典的压缩算法。通过字符出现的频率，优先级，二叉树进行的压缩算法。

对一个字符串，计算每个字符出现的次数, 把这些字符放到优先队列（priority queue）这这个 priority queue 转出二叉树

需要一个字符编码表来解码, 通过二叉树建立 huffman 编码和解码的字典表

字典树 trie (前缀树，单词查找树) @

trie，又称为前缀树或字典树，是一种有序树，用于保存关联数组。

除根节点不包含字符，每个节点都包含一个字符
从根节点到某一个节点，路径上经过的字符连接起来，为该节点对应的字符串
每个节点的所有子节点包含的字符都不相同（保证每个节点对应的字符串都不一样）

比如：

                    / \
                   / | \
                  t  a  i
                /  \     \
               o    e     n
                   /|\    /
                  a d n  n

上面的 Trie 树，可以表示字符串集合{“a”, “to”, “tea”, “ted”, “ten”, “i”, “in”, “inn”} 。

trie 树把每个关键字保存在一条路径上，而不是一个节点中。两个有公共前缀的关键字，在 Trie 树中前缀部分的路径相同，所以 Trie 树又叫做前缀树（Prefix Tree）。

子树用数组存储，浪费空间；如果系统中存在大量字符串，且这些字符串基本没有公共前缀，trie树将消耗大量内存。如果用链表存储，查询时需要遍历链表，查询效率有所降低

trie 树的增加和删除都比较麻烦，但索引本身就是写少读多，是否考虑添加删除的复杂度上升，依靠具体场景决定。

它的优点是：

插入和查询的效率很高，都是 O(m), 其中 m 是待插入 / 查询的字符串的长度
Trie 树可以对关键字按字典序排序
利用字符串的公共前缀来最大限度地减少无谓的字符串比较, 提高查询效率

缺点：

trie 树比较费内存空间，在处理大数据时会内存吃紧
当 hash 函数较好时，Hash 查询效率比 trie 更优

典型应用是：前缀查询,字符串查询，排序

用于统计，排序和保存大量的字符串（但不仅限于字符串）
经常被搜索引擎系统用于文本词频统计
排序大量字符串
用于索引结构
敏感词过滤

实际应用问题

给你100000个长度不超过10的单词。对于每一个单词，我们要判断他出没出现过，如果出现了，求第一次出现在第几个位置

分析思路一：trie 树，找到这个字符串查询操作就可以了，如何知道出现的第一个位置呢？我们可以在 trie 树中加一个字段来记录当前字符串第一次出现的位置。
已知 n 个由小写字母构成的平均长度为 10 的单词, 判断其中是否存在某个串为另一个串的前缀子串
给出 N 个单词组成的熟词表，以及一篇全用小写英文书写的文章，请你按最早出现的顺序写出所有不在熟词表中的生词。

分析：trie 树查询单词的应用。先建立 N 个熟词的前缀树，然后按文章的单词一次查询。
给出一个词典，其中的单词为不良单词。单词均为小写字母。再给出一段文本，文本的每一行也由小写字母构成。判断文本中是否含有任何不良单词。例如，若 rob 是不良单词，那么文本 problem 含有不良单词。

分析：先用不良单词建立 trie 树，然后过滤文本 (每个单词都在 trie 树上查询，查询的复杂度 O(1), 效率非常高)，这正是敏感词过滤系统 (或垃圾评论系统)的原理。
给你 N 个互不相同的仅由一个单词构成的英文名，让你将它们按字典序从小到大排序输出

分析：这是 trie 树排序的典型应用，建立 N 个单词的 trie 树，然后线序遍历整个树，就可以达到效果。

后缀树（suffix tree） @

后缀树的应用

可以解决很多字符串的问题

查找字符串 S1 是否在字符串 S 中
指定字符串 S1 在字符串 S 中出现的次数
字符串 S 中的最长重复子串
2 个字符串的最长公共部分

数据库系统中的算法 @

最近开始读《数据库系统实现》这本书，所以就想到把数据库里面用到的数据结构和算法做一个梳理。就有了这些文字。

电梯算法

B 树索引

R 树索引

位图索引

一趟算法

二趟算法

基于排序

基于散列

连接树

动态规划

贪婪算法

分布式并行数据库中的任务分配算法

并行算法

数据挖掘

发现频繁项集的算法

发现近似商品的算法

PageRank

refs and see also

《数据库系统实现》
《redis 设计与实现》

refs and see also

nonstriater/Learn-Algorithms: 算法学习笔记

问答 | 九章算法 ♥️ @

概率论问题 ♥️ @

假设有一个硬币，抛出字（背面）和花（正面）的概率都是0.5，而且每次抛硬币与前次结果无关。现在做一个游戏，连续地抛这个硬币，直到连续出现两次字为止，问平均要抛多少次才能结束游戏？注意，一旦连续抛出两个“字”向上游戏就结束了，不用继续抛。

假设连续抛 2 次正面的期望为 E

E = 0.5 * 0.5 * 2     (第一次抛了正， 第二次也抛了正，则抛两次结束了，次数是两次)
  + 0.5 * 0.5 * (E + 2)（第一次抛了正， 第二次抛了反，前面无效了，从头开始，那么再出现两个正面，次数是 E+2）
  + 0.5 * (E + 1)      (第一次抛了反， 前面无效了，从头开始，那么再出现两个正面次数是 E+1）

E = 6

同理可以推算连续三个正面，连续反正，正反，等等所有情况都可以计算。

谢谢助教，

比如三个正面应该就是这四种情况分析了把？(反正以遇到反就要从头开始弄了)

正正正

正正反 + E

正反 + E

反 + E

同理算一样连续三个正面的期望 E

E = 0.5 * 0.5 * 0.5 * 3
  + 0.5 * 0.5 * 0.5 * (E + 3)
  + 0.5 * 0.5 + (E + 2)
  + 0.5 * (E + 1)

得到 E = 14，三个连续正面的期望是 14 次。

refs and see also

怎么找中小公司校招的职位？ @

大公司可以去他们网站投，不过那些不知名的中小公司的校招职位怎么找呢？Indeed 之类的上面搜什么关键词？

angellist

【置顶】为什么不需要学习贪心法 @

因此，贪心法可以说，是一种“目光短浅”的算法。一般在算法问题中，可以使用贪心算法的问题，其贪心策略往往都比较复杂，一般人是想不到的。而你容易想到的那些贪心策略，往往都是错的。

面试基本不会考 @

贪心法的问题，面试基本不会考，因为等同于考智力题或者是背诵题。一个面试官想要自己凭空创造出一个面试题是使用贪心算法的，是非常困难的。（参见 LintCode 上的贪心算法的题目所占比例可知）。既然如此，如果面试中被问到了贪心算法，那么一定是一道经典的贪心问题，这类问题，我们可以称之为背诵题。因为大多数同学（除了智商很高，或者有算法竞赛经历的那一批），是不可能在面试的时候想得出解法的。

举几个例子：Gas Station (http://www.lintcode.com/en/problem/gas-station/)，这个题的做法是，从任意站点出发，走一圈，找到这一圈里剩余Gas最少的那一站，然后从这一站出发走一圈，如果在这一站出发可以顺利走完全程，那么就可以行，否则就不可行。像这样的算法，是需要进行数学证明来证明其正确性的，面试官是没有能力出这样的面试题的。

从另外一个角度来说，贪心算法的题，对于程序的实现能力要求并不高，也违背了公司通过算法题面试主要是希望考察大家的程序实现能力这一点。所以面试官和公司也都不倾向于将贪心算法作为面试的算法问题。

没有通用性 @

二分法，动态规划算法，分治算法，搜索算法等等，很多的算法都是具有通用性的。也就是说，在题目 A 里，你用了这个算法，在其他的题目 B 里，你可能完全可以用一样的算法和思路去解决。

而贪心法，他不是“一个算法”，而是“一类算法”的统称。所以基本的情况就是，你在题目A里用了某个贪心算法解决了这个问题，然后这个题中用到的贪心法，永远也找不到第二个题用类似的方法来解决。

贪心是动态规划的子集么? @

只要问题的解决方案有最优子结构，并且无后效性就可以认为是动态规划。

但是你这样问并没有什么意义，因为动态规划真正的目的还是依赖空间换时间，而贪心策略不是。

举个简单的例子来说，求单源最短路的 Dijkstra 算法，你可以认为它是一个贪心算法，因为根据定义（Di 表示源点到节点 i 的最短路长度）：

Dj = min{ Dj, Di+ Matrix[i][j] }

它每次迭代都很无脑地选一条最近的路出发，所以认为是一个贪心策略。但是它又有效地将重叠的最优子结构问题用一个辅助数组 D 存储了起来，并且没有后效性，所以也是一个动态规划算法。

如何理解动态规划？ :TODO: @

TODO

refs and see also

resume 上需要写 objective 吗 @

听九章的讲座说要写，但是九章给的简历里又没有 objective。是不是转专业的必需写？

要。

多个面试经验贴汇总 @

第一档次: Dropbox, Square, Pinterest, Facebook, LinkedIn, Google, Twitter, Apple
第二档次: Zynga, Yelp, Netflix, Skype, VMWare, Salesforce, Groupon, Paypal, Evernote, Box.net, Quora, A9.com, 126Lab, Palantir
第三档次: Oracle, EMC, eBay, Intuit, NetApp, NetSuite, Yahoo, Adobe, Autodesk, Symantec, Riverbed, Quantcast, Concur, Aster Data, Citrix, EA等

算上湾区以外公司， Amazon, Micriosoft 可以排在第二档次 Expedia, RedHat, RackSpace, Akamai, Bloomberg 等可以排在第三档次。

Dropbox 创始人 Drew Houston 在 2013 年 MIT 的毕业典礼上讲的很好：“世界上只有一个好莱坞，一个硅谷，如果你想待在业界最好的圈子，那就搬家！”我被他说服，投简历的时候瞄准了 FLGT(业界最火的四家公司， Facebook, LinkedIn, Google, Twitter) 和一众火爆的初创公司。

最近细读未来公司 LinkedIn 的创始人 Reid Hoffman 的新书 The Start-up of You，里面讲到求职三片拼图：你的资源 / 能力（your assets），你的志向 / 价值观（your aspirations/values) 和市场现实（market reality），共同组成你的核心竞争力。所以我去尝试互联网大公司，十投八中，但是其他的努力很多都浪费了，如果当时早就看了这本书多好。关于这本书和它的作者，以后会写另一篇文章详述，这里先隆重推荐给大家。

最后来一点干货吧，给本专业的人看 @

Google 题目： @

MST of a all connected graph. Need to use Fibo heap to reduce complexity.
Game of Life, one transition (sub O(n^2) solution).
String compressor that turns 123abkkkkc to 123ab5xkc. Decompressor is already written and must remain unchanged. (messy code)
Youtube mash design, how to do a video version of Mark’s FaceMash.

题全都没见过，rej

Facebook 题目： @

电话

Big Integer multiplication. (Optimization required, how to do 8 digits*8 digits, etc).
Binary tree level order traversal. (leetcode original)
也是 leetcode 原题，不记得了

Onsite

Given 1->a, 2->b … 26->z. 126 -> az or lf or abf (bfs/dfs not accepted, need to use DP or some tricky method)
Binary tree serialization/de-serialization (这道题pinterest也问了）
Permutation with duplicate
Range maximum query, pre-processing in O(n) and query in O(1)

题答少了一道，rej

其他重要题目和技巧：

2Sum 3Sum, rotate LinkedList, minimum path sum, combinations

注重练习 tree 的 recursion 搜索, dp, greedy, two/three pointers, stack. 谷歌的题是很难刷到的，要靠运气，其他很多公司（尤其是亚马逊为首）都可以靠刷题大幅提高胜算。资源：leetcode.com, geeksforgeeks.com, glassdoor.com, CC150

BTW，今年几家的硕士 package 都差不多，大约是 115k base + 160-170k （RSU 股票分4 年 + signing + reloc)，如果没有 competing offer 比较难negotiate。我的 O 家offer 是 114k base + 4000 股期权分四年 + 15k signing + 10k reloc，在等 LinkedIn发 official offer 之前，成功的想办法把 deadline 延长了两次，变成 Standing offer，如果不这么干，他们是愿意涨一点 base 的。

按照我个人的理解，学生被大公司分两类，第一类是“名校 GPA3.8 以上”的，第二类是else。作为 else 的代表，我不得不说，GPA3.8 以上真的很难，第一类们确实确实有特权先被考虑，但本文正是献给广大 else 们的。

面试这个东西，其实是没法准备的，全靠经验。我没有哪个问题在第一次被问的时候就能答的很完美，我相信谁也不能。从去年 6 月跟人家介绍自己都要磕磕巴巴，到现在基本我虐面试官，大大小小的电面一百来次，onsite 十来次，磨厚的不只是嘴皮，还有脸皮。其实面试的最高奥义就是厚着脸皮吹牛逼，并用丰富的吹牛逼经验保证不被拆穿即可。当然了，知识还是要有一些，毕竟是技术职位，而且要对 Coding 有一腔热情。当然了，还要习惯每天吃 subway。

在这里我想说一说老中，我所说的老中是指现在 40-50 岁，30 多岁的时候从国内直接跳槽过来的中国软工，错了，是我们这儿软工。我去 qualcomm 和 amazon onsite 都是栽到了老中手里。我现在也不明白为什么只有中国人看不上中国人，而人家阿三都是只帮阿三。我在 qualcomm 最后一个面的老中问我，有没有学过 OS，我说我自学的。他说你没有做过那些 project 也说你学过？我说你可以问啊，看看我会不会。结果这 B 问了我一堆我回来 google 都查不到的鬼问题，还问我 how to simulate garbage collector in C? 看我不会又得意洋洋的反问我，你没学过 OS 还想找 SWE 的工作? 我就说我的课都是 application level 的。他操着浓重的不知哪的方言腔说了一句让我一辈子都忘不了的话：If I wanna build a applicaiton, I will go to hign school and ask them “Who wanna do some funny stuff?”. Why I hire you? 我擦，我当时真想一口大浓痰吐他脸上然后大骂我去你大爷的。但是我还是忍住了，虽然我从他眼睛里也能看到我眼里冒出的火光。Amazon 也是一样的，在其他面试官都被我折服之后，他又问我为什么 EE 的不好好学 EE，CS 的基础课你都没学过云云…. 我当时以为我面的可以，因为他的题被我做完了，我还挑了他一个错误。事后我感觉挑他的错这一下让他决定毙我的，要不然，就是和我竞争的人过于 NB 了。

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

美团 2015 校招面经 - 软件研发岗 (拿到 offer) @

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

Linkedin 面经合集 @

面经 1 @

然后就是开始做题，两个题目。

第一个是两个单词最短距离，在版上看到很多人都说过这个题目，应该是L家经常面的。本来以为只要实现一个函数，哪里知道是实现两个函数，第一个是做求最短距离的准备工作，实现类的初始化；第二个才是真正的求最短距离的函数。写第二个函数的时候，还忘记判断单词是否在字典中出现过，幸好面试官有提醒。

第二题就是 leetcode 上的全排列，没有重复元素的。

面经 2 @

第二题也比较常见,CC150 原题, 找俩字符串在一段文字中最近的距离:

直接用 CC150 解法, 用两个 index 比较得出 Math.abs(index1-index2), update 最小距离. 写好后提示要是 cat dog cloud dog dog dog……, 即后面有 million 个 dog, 是否不用比较整个文章. 回答说用 map 提早存储每个单词的 index, 然后在 map 中找到单词比较, 在讨论后最坏情况下复杂度也是 O(n).

由于没有时间写代码了所以这样结速了.

面经 3 @

就一道题，经典的求minimum word distance. 但是一开始有挺多有关ML的细节题

实现 BlockingQueue 的 take() 和 put()

public interface BlockingQueue<T>
{
    /** Retrieve and remove the head of the queue, waiting if no elements
    are present. */

    T take();

    /** Add the given element to the end of the queue, waiting if necessary
    for space to become available. */
    void put (T obj);
}

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

Google 15 Fall SDE I 实习生电面 @

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

G 家面经题，矩阵最小 @

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

Compress String ♥️ @

给一个 string，要求压缩后最短。比如说对于 aaaa，4[a] 肯定要比 2[aa] 要好。我除了暴力枚举 substring 以外想不到任何其他方法，请问助教有没有其他想法？

本问题可以简化成 S = a[substring], 求最大的a。

如果学过 KMP 算法的，求出 S 的 next 数组。

n = len(S)
    j = next[n]
while   n % (n - j) != 0:
        j = next[j]

    a = n / (n - j)

这是由 next 数组的性质决定的，可以先学一下 KMP 算法。

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

无实习开源经验 GPA 不高的小硕的 FLAGBR Offer 经 @

拿了 FLAGR 的 offer，B 家主动 cancel 了 onsite。非常幸运，面了的公司都拿了 offer，最终去了最喜欢的 F 家，多要了一点 sign on，因为穷的太久了，急需点钱来玩。对于package 来说，基本都是标准 package，开始的时候 F 最多，后来 G 给加了不少，最终拒绝G 的时候还要再给加，感觉 G 很喜欢抢 F 的人啊！钱多钱少不太看重，反正也不准备长期做码农。自己感觉的 hiring bar 的排序： facebook=linkedin>google>amazon, 当然，难度是随着时间改变的，招人多的时候容易，不怎么招人的时候就很难。

Facebook

签了 offer，就不透露题了，总之感觉 facebook 的 bar 最高，面试题的难度不同人差别很大，题目简单不一定就有 offer，题目难也未必没 offer，不好说。

第一题：贪心

    Given a number, can you remove k digits from the number so that the new
    formatted number is smallest possible.
    input: n = 1432219, k = 3
    output: 1219

第二题：DP

    BT(binary tree), want to find the LIS(largest independent set) of the BT
    LIS: if the current node is in the set, then its chilren should not be in
    the set. So that the set has the largest number of nodes.

电面2：

    第一题：Median of Two Sorted Arrays
    第二题：DP，一个二维数组，元素是 0 或 1，找出最大的由 1 构成的"X"形状

onsite:

1. print all subsets
   system design(N topics, publishers, subscribers, scalability, distributed)
   the most frequent urls in the past minute, hour, day
2. manager interview
   code review
3. shortest path between two nodes of a tree(no parent pointer)
4. machine learning(不懂)
5. machine learning(不懂)

Rocket Fuel是自己投的，因为在网上看到code challenge挺有意思。onsite的时候了
解到他家最近要搬进新楼里，应该招人很多，大家可以试一试，题目不简单

Google:

电面：
remove duplicate lines of a file(what if the file is very large which could
not be held in the main memory)

开关灯问题
Trapping Rain Water(leetcode)
sometimes a program works, sometimes it does not. Possible reasons

onsite:
1. clone directed graph(recursive, non-recursive)
   longest common suffix of two linked list
   data structure design
2. how many (m, n) pairs such that m*m+n*n<N
   线索化二叉树
3. 判断一个点是否在一个凸多边形内, O(n), O(logn)
4. group items(BFS)
   MapReduce(filter a collection of documents, the words which occur more
than 5000 times)

google 面的不好，因为实在是太累了，幸运的是还是给 offer 了。

linkedin

电面 1：

第一题：给一个 words list, 输入两个单词，找出这两个单词在 list 中的最近距离 (先
写了一个没有预处理的，又写了一个预处理建 index 的)
['green', 'blue', 'orange', 'purple', 'green']  f.distance(list, 'blue', ' green') # output 1

第二题：类似 binary search 的一题，要注意 boundary case

电面2：

binary tree level order traversal, 写了三种方法。。。(BFS 用 arraylist，类似 DFS，BFS 用 queue)

onsite:
1. romanToInt, intToRoman,
   N points, m nearst ones
2. 双向链表，每个node可能都有父节点和子节点，每个父子节点又是一个链表。把它拍扁，顺序随意，O(1)空间复杂度
   edit distance
3. system deisign: design amazon product page
4. project presentation
5. group fit

LinkedIn 很不错，食堂很好吃，并没有传说中的那么多印度人，国人挺多的。听 hr 说
linkedin 今年要扩大技术团队，大家可以投一下

找工作经验：

不要把战线拉的太长，2 个月最好，时间久了就没有激情了，效果反倒不好。准备的时候要全力以赴，concentration
安排面试最好不要把所有公司放在同一周，实在是太累了，最好是两个 onsite 之间间隔两天
对于男生来说，准备面试无聊的时候可以做做俯卧撑和卷腹，即使拿不到 offer 还能练出胸肌和腹肌~
CC150 随便看看就行了，leetcode 要“好好”做 (融会贯通)，面试一家公司之前看看相应的面经，足够了
如果不是搞 acm 的，leetcode 至少要刷一遍再去面 flag。刷几遍不关键，关键是要有提高
提高两方面：
1. coding 能力：会做的题能写出 bug free，简洁可读性好的代码
2. 算法，解决问题的能力：没见过的题，一步一步想到面试官想要的方法
coding 能力：写的程序越短越好，思路清楚，容易看懂；可以写多个函数，可读性好很多，写起来也容易；争取一遍写完就 OK，不要改来改去；我感觉 coding 能力的重要性被大家严重低估了，很多人只关心算法，其实能把程序写的干净漂亮才是最关键的。
算法，解决问题的能力：即使见过的题也要一点一点的分析，面试官看重的是分析和交流的过程，而不是最终的 solution；不要只知道多做题，要多思考，这个和高考一样，翻来覆去就是几种类型的题，按照类型来做，很快就熟练了
和面试官聊的开心很关键，要表现出积极，乐观，阳光，热爱生活，让面试官 enjoy 面试过程，喜欢和你一起工作
不要抱怨，不要给自己找借口

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

Facebook onsite 面经 @

第一轮 @

老印，上来一道题，讲了半天我才弄明白。类似手机按键，比如手机按键上 2 对应 ‘abc’, 然后根据‘abc’的顺序，打出 a 要按一下键，b 要按两下键，c 要按三下键。给你两个数组: keySize[] 每个 element 代表能存放的最多 character，frequency[] 每个 element 代表每个 character 出现的频率。要算出最少的按键次数。

Follow up 1: 怎么能提高效率。

Follup up 2: 如果要求 character 放在按键上的顺序是 order 的，类似于手机 shang 的字母按键，这样最少按键次数是多少。

第二轮 @

还是个烙印：第一题：rotated sorted array search. 让后要求 cut branch。第二题： sort an array contains only 3 element，类似 leetcode 的 sort colors。 follow up: what if there are N element? 没想出来， hint 是可以使用 extra memery。

第三轮 @

简历问题为主，问了一道 code： check the first bad version.

结果还是跪了。问题应该出在第一轮面试上，code 写了好久才写出来，follow up 也没答上。其实题目也不算很难，大家好运吧。

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

微软 ots，已挂，求分析一道题 @

最近做微软的 OTS，一共三道题。

给你一个时钟，返回一个 palindrome 的时间。比如 1:01，12:21
排序 2d 数列，返回负数的数量。
碰到一题算是系统设计题吧。只有两三句话：用熟悉的语言写一个 email 的 api 服务。写出实现的场景以及需要用到哪些参数。

已挂，估计是挂在第三题。前两题都做过差不多的。第三题不是很懂题目要我做什么，因为是在线面试，没法和面试官交流。不是很清楚需要写什么。。。求大家一起讨论下。我用java写了个几个接口。然后今天接到通知面试挂了。不是很清楚应该怎么做这种题。我当时代码大概如下

比如我实现了 get email 的 api，但不知道具体 api 里面该写些什么。需要连数据库还是啥的？

class user {
    int userID;
    String userName;
}

class email {
    int emailID;
    String emailAddress;
    String subject;
    Date timestamp;
    String content;
    int from_userID;
    int to_userID;
}

public List getEmail (int userID) {
    return db.getEmail(userID)
}

public List getEmail (int userID, Date startDate, Date endDate) {
    return db.getEmail(userID, startDate, endDate);
}

public List getEmail (int userID, int getEmailNum) {
    return db.getEmail(userID, getEmailNum);
}

自己看着感觉都不怎么符合要求。能有人指点一下正确写法改如何写吗？谢谢了！

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

第一堂课 Design Twitter @

存在 NoSQL DB 的 Tweet 是每一个 Tweet 对应一行吗，还是每个用户对应一行？这样的话 row key 是什么呢？是 user_id？如果是，然后 column key 是 tweet id，因而可以支持范围查找？如果是范围查找的话，timeline 的请求为什么需要 n 次的 DB 访问时间（mentioned in p41 in the slides）？

每个用户一行，然后有无限列。

row_key = user_id
column_key 可以是tweet_id，也可以是一堆数据的组合，比如tweet_id + timestamp。
column_key 可以支持范围查找。

P41 这里说的是，当你需要构建一个 NewsFeed 的时候（你关注的 N 个好友的所有新鲜事汇总），需要 N 次 DB 请求去分别请求每个好友的最近 100 条 tweets 然后再归并到一起。请求某一个用户的 timeline 是一次 Query，请求 N 个用户，就是 N 次。这里的 N 说的是你的好友个数。

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

应届生国内找国外工作求职网站有哪些 @

我是一名国内的应届硕士毕业生，九月要开始投简历了。问一下，想直接找国外工作的话，有哪些好的网站可以推荐？目前只看到了 google 有正式的全球招聘途径，其它公司的如何能看到？linkedin 等上面的职位是不是都是针对有在美国工作资格的才能申请？

http://stackoverflow.com/jobs?med=site-ui&ref=jobs-tab

谢谢啦，请问 VISA SPONSOR 是不是指可以提供抽签证的机会？

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

yahoo 面试经验 @

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

腾讯面经，拿到 offer @

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

东邪老师第二节课 Friendship 相关的问题 @

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

剩下不到一個月時間 interview 請問怎麼準備? @

已經刷題一陣子. 但是一些比較難的和 graph, DP 都還不行, 有什麼好建議?

那就不要看 Graph 和 DP 这类考得很少的问题。多看 DFS / BFS 这类问题。

Uber 面试题房屋窃贼 House Robber II ♥️ @

小偷找到了一个新的偷盗地点，这个地区的房子组成了一个环，如果小偷同时偷窃了两个直接相邻的房子，就会触发警报器。在不触发警报器的情况下，求小偷可以抢到的最多的 money。

解题思路

本题是 House Robber 的 follow up。

House Robber-i 中房子排列成一个序列，用动态规划就可以，上过《九章算法强化班》的同学应该都已经会做啦。

按照课堂上讲过的动态规划四要素说说 dp 状态的定义：

df[i] 表示前 i 个房子能获得的最大价值，
dp[i] = max(dp[i-2] + nums[i], dp[i-1])。

而在本题中，房子难点在于排列成一个环。对于环上的问题，有一个小技巧就是就是拆环：把环展成一条直线。

本题中，可以先假设房子排成一条直线，从 0 到 n-1，那么我们如果用原来的动态规划算法求得的最优解可能同时取到房子 0 和房子 n-1，而因为 0 和 n-1 在本题中是连在一起的，不能同时取到。也就是说，我们要分两种情况：要么不偷房子 0（此时房子 n-1 是否偷未知），要么不偷房子 n-1。基于这两种情况，我们对不含房子 0 的序列做一次动态规划，对不含房子 n-1 的序列做一次动态规划，取较大值就可。

参考程序 http://www.jiuzhang.com/solutions/house-robber-ii/

面试官角度分析：本题是一个 follow up，在解决 robber-i 的情况下，对于环的特殊性给出解决方法，实现 O(n) 算法可以达到 hire。

LC 相关联系题：https://lintcode.com/problems/house-robber/

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

怎么准备多线程的问题 @

最近好多朋友面试都被问到了线程的问题，比如让你写一个比较简单的字符串处理的程序，可能涉及到哈希表之类的，然后紧接着问你如果多线程怎么实现？或者问你线程如何才能安全。

因为关于线程只了解生产者消费者，平时工作中用的也不多，请问有关于最近频繁出现的多线程问题应该怎么准备？有什么材料或者推荐么？

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

微软面经 @

这家面试轮数较多，从学校开始，面了很多经典问题。数组里找最大和的序列，何时买卖股票，两个链表是否有公共 Node，二分查找（数组很大，你需要考虑 sort 成本，什么时候 sort 才有意义，比如你 query 的次数很多很多，那么一次性sort 一下是有必要的），二位已排序矩阵中如何快速查找一个数，计算泰勒展开，计算 N*M 矩阵的所有子矩阵。微软很注重写完 code 以后测试，一定要留些时间给测试，一般来说白板上写的 code 小毛病都会有好几处，通过自己测试是可以改过来的。

一些操作系统原理，我不会，选择不作答，感觉没甚影响。

我因为长时间不用 C++，可以说目前已经不会 C++，只会 JAVA，起初很虚，但是后来微软对不编程语言要求很松，重要的是解释问题要解释得很清楚。所有面试官都思路很清晰，【你解释不清楚，他会直接打断你，不要想着糊弄】。如果不清楚，直接承认，这是我从已经拿到全职的朋友那儿听来的经验，算是微软的风格吧。

【时间复杂度，当然，每一步操作都会问你时间复杂度】，逃不掉的。对哈希表，有一个面试官表现出明显的不喜欢，这时候我换思路了，虽然那道题目哈希表做很容易，但是没办法，人家是面试官。

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

面试时如何有条理的组织 test case 啊 @

Test case 有以下几种

边界数据，比如 n = 0 这些边界情况
特殊数据，比如链表中我们删节点需要删除 head 的时候
大数据，一般测试算法效率

面试的时候，我们只需要给出边界数据，特殊数据，和一些普通数据即可。

豆瓣面试题 :分段筒排: @

给定 10G 个无符号整数 (32 位)，如何能够最快地在一台内存为 2G 的机器上找到这些数据中的中位数 (比一半数据大，比另一半数据小)，这个感觉似曾相识，又想不出是哪个方面的知识, 助教老师能否解答下？

这个是古董的不能在古董的题目了。常用做法就是【分段桶排】

更详细的可以看这个文章，我就不复制过来了。

http://www.cnblogs.com/avril/archive/2012/04/20/2460805.html

refs and see also

10G 个整数找出中位数，内存限制为 2G - Avril - 博客园

leetcode 面试题 38 洗牌的技巧 @

有一副扑克有 2n 张牌，用 1,2,..2*n 代表每一张牌，一次洗牌会把牌分成两堆， 1,2..n 和 n+1…2n。然后再交叉的洗在一起：n+1, 1, n+2, 2, … n, 2n。问按照这种技巧洗牌，洗多少次能够洗回扑克最初的状态：1,2,…2n。

以 1 2 3 4 5 6 为例，洗一次之后为 4 1 5 2 6 3 。将两排数组对比看：

1 2 3 4 5 6 4 1 5 2 6 3

数字 1 的下面是 4，代表每一次洗牌后 1 这个位置的数会被 4 这个位置的数替代，接着看数字 4，4 下面是 2，代表每一次洗牌后 4 这个位置的数会被 2 替代，再看 2，2 下面是 1，2 这个位置的数字会被 1 替代。此时，1 4 2 形成一个环，代表这三个位置上的数再每一次洗牌后，循环交替，并且在洗 3 次以后，各自回到最初的位置。用同样的方法可以找到 3 5 6 是一个循环，循环节长度为 3。由此可以知道，在经过了 LCM(3,3)=3 次洗牌后，所有数都回到原位，这里 LCM 是最小公倍数的意思。于是算法为，根据一次洗牌的结果，找到所有的循环节，答案为所有循环节长度的最小公倍数。

面试官角度：

这个题目的考察点在于找规律。不过如果有一定置换群的理论基础的同学，是可以比较轻松的解决这个问题的。有兴趣的同学可以查看离散数学的相关书籍中置换群的知识点。

1 2 3 4 | 5 6 7 8 5 1 6 2 6 3 8 4

1->5->6->3->6 2->1->5->6->3->6

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

leetcode 面试题 40 不用除法求积 @

给定一个数组 A[1..n]，求数组 B[1..n]，使得 B[i] = A[1] * A[2] .. * A[i-1] * A[i+1] .. * A[n]。要求不要使用除法，且在 O(n) 的时间内完成，使用 O(1) 的额外空间（不包含 B 数组所占空间）。

计算前缀乘积 Prefix[i] = A[1] * A[2] .. A[i]，计算后缀乘积 Suffix[i] = A[i] * A[i+1] .. A[n]，易知，B[i] = Prefix[i - 1] * Suffix[i + 1]。实际上无需实际构造出 Prefix 和 Suffix 数组，利用 B 数组从左到右遍历一次得到 Prefix[i]，然后从右到左遍历一次，计算出所要求的 B 数组。

面试官角度：

这种从前到后遍历和从后到前再遍历一次的方法（Foward-Backward-Traverse）在很多题目中都有借鉴。如九章算法面试题31 子数组的最大差。

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

Perfect Squares 这道题的思想及状态转移方程怎么想？ @

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

关于 design Google suggestion sharding 的问题 @

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

根据字符串表达式计算字符串 @

yahoo onsite 题目，给出表达式，由数字和括号组成，数字表示括号里面的内容（可以是字符串或者另一个表达式）重复的次数，表达式和字符串可以混合，比如：

3[abc] => abcabcabc
4[ac]dy => acacacacdy
3[2[ad]3[pf]]xyz => adadpfpfpfadadpfpfpfadadpfpfpfxyz

尝试用了递归发现做不出来。。然后用 stack 解决了一部分 case，但是另一部分 case 不适用。。。求高人指点，万分感谢！

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

将一个字符串形式的十进制数转换成 7 进制的字符串 @

例如: 十进制的 “123” 转为七进制的 “174”。

follow up: 如何修改使之可以满足任意进制间的转换。

123 / 7 = 17(商).....4(余数)
17 / 7 = 2(商).....3(余数)
2 / 7 = 0(商).....2(余数)

所以对应的 7 进制是 “234”， 2 * 49 + 3 * 7 + 4 = 123（10 进制）

同理79：

79 / 7 = 11(商).....2(余数)
11 / 7= 1(商).....4(余数)
1 / 7 = 0(商).....1(余数)

所以对应的 7 进制是 “142”， 1 * 49 + 4 * 7 + 2 = 79（10 进制）

所以 10 进制转换成 B 进制，就是除 B 取余倒序。

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

窗口类 two pointer @

在课间中的窗口类 two pointer，minimum-size-subarray-sum 这道题中提到了窗口类和 sliding windows 的区别，请问这个区别在哪？现在不记得上课怎么讲的了。。。

线段树 (Segment Tree、Binary Indexed Tree)、Trie、Union Find 这些特殊数据结构需要掌握到什么程度 @

如题，线段树(Segment Tree、Binary Indexed Tree)、Trie、Union Find这些特殊数据结构需要掌握吗？如果需要的话，需要掌握到什么程度？会用、知道原理、会实现等等。

如果你上的是强化班你建议做一做 Ladder 里面线段树相关的题目。

LintCode 线段树的题目： http://www.lintcode.com/en/tag/segment-tree/

我觉得并不是太重要，首先线段树考的频率不高，如果一些高频算法你掌握的很好了，学一下当然更好，不光光线段树的问题可以解决，其他很多问题也能用线段树优化，肯定能为你面试加分。其他高频算法还没掌握好，建议可以放一放。

一般线段树用于解决与区间有关的问题，Lintcode 上如果做过了基础线段树题目还可以做其他的如：

http://www.lintcode.com/zh-cn/problem/interval-minimum-number/
http://www.lintcode.com/zh-cn/problem/interval-sum/
http://www.lintcode.com/zh-cn/problem/interval-sum-ii/
http://www.lintcode.com/zh-cn/problem/count-of-smaller-number/
http://www.lintcode.com/zh-cn/problem/count-of-smaller-number-before-itself/

我都找完之后才发现 Lintcode 的 Tags（标签）功能还是很好用的！

leetcode 面试题 29 子矩阵的最大公约数 @

给定 n*n 的矩阵，需要查询任意子矩阵中所有数字的最大公约数。请给出一种设计思路，对矩阵进行预处理，加速查询。额外的空间复杂度要求 O(n^2) 以内。

构建二维线段树。预处理时间 O(n^2)，每次查询 O(log n)

面试官角度：

这个题目需要具备一定的数据结构功底。线段树 (Interval Tree) 可以解决的问题是
那些满足结合律的运算。最大公约数是一个满足结合律的运算。所以有，
GCD(A,B,C,D) = GCD(GCD(A,B), GCD(C, D)) 。同样具备结合律的运算有
PI,SUM,XOR(积, 和, 异或)。线段树的基本思想是，将区间 [1,n] 查分为 [1, n/2],
[n/2+1,n] 这两个子区间，然后每个子区间继续做二分，直到区间长度为 1。在每个
区间上维护这个区间的运算结果（如 GCD,SUM)，需要查询某一段区间的结果时，将该
区间映射到线段树上的若干不相交的区间，将这些区间的结果合并起来则得到了答案。
可以证明任何一个区间可以映射到线段树上不超过 O(log n) 个区间。上面介绍的是
一维的线段树，对于二维的情况，可以采用四分或者横纵剖分的方法来构建线段树。

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧

MISC @

此题的最优算法是贪心。在实际面试过程中，笔者认为只需要想到贪心算法，并给出算法框架，就可以达到【hire】的程度。能在短时间内完成程序，可以达到【strong hire】。

refs and see also

问答 | 九章算法 - 帮助更多中国人找到好工作，硅谷顶尖 IT 企业工程师实时在线授课为你传授面试技巧

AVL 树，红黑树，B 树，B+ 树，Trie 树都分别应用在哪些现实场景中？ @

AVL 树: 最早的平衡二叉树之一。应用相对其他数据结构比较少。windows 对进程地址空间的管理用到了 AVL 树。AVL 是一种高度平衡的二叉树，所以通常的结果是，维护这种高度平衡所付出的代价比从中获得的效率收益还大，故而实际的应用不多，更多的地方是用追求局部而不是非常严格整体平衡的红黑树。当然，如果场景中对插入删除不频繁，只是对查找特别有要求，AVL 还是优于红黑的。

红黑树: 平衡二叉树，广泛用在 C++ 的 STL 中。map 和 set 都是用红黑树实现的。还有

著名的 linux 进程调度 Completely Fair Scheduler, 用红黑树管理进程控制块
epoll 在内核中的实现，用红黑树管理事件块
nginx 中，用红黑树管理 timer 等
Java 的 TreeMap 实现

B/B+ 树用在磁盘文件组织数据索引和数据库索引

Trie 树：字典树，用在统计和排序大量字符串 (场景自己 yy = =)，trie 树的一个典型应用是前缀匹配，比如下面这个很常见的场景，在我们输入时，搜索引擎会给予提示，还有比如 IP 选路，也是前缀匹配，一定程度会用到 trie。

红黑树，AVL 树简单来说都是用来搜索的呗。

AVL 树

平衡二叉树，一般是用平衡因子差值决定并通过旋转来实现，左右子树树高差不超过 1，那么和红黑树比较它是严格的平衡二叉树，平衡条件非常严格（树高差只有 1），只要插入或删除不满足上面的条件就要通过旋转来保持平衡。由于旋转是非常耗费时间的。我们可以推出 AVL 树适合用于插入删除次数比较少，但查找多的情况。

红黑树

平衡二叉树，通过对任何一条从根到叶子的简单路径上各个节点的颜色进行约束，确保没有一条路径会比其他路径长 2 倍，因而是近似平衡的。所以相对于严格要求平衡的 AVL 树来说，它的旋转保持平衡次数较少。用于搜索时，插入删除次数多的情况下我们就用红黑树来取代 AVL。

（现在部分场景使用跳表来替换红黑树，可搜索“为啥 redis 使用跳表 (skiplist) 而不是使用 red-black？”）

为啥 redis 使用跳表 (skiplist) 而不是使用 red-black？ - 知乎 @

在 server 端，对并发和性能有要求的情况下，如何选择合适的数据结构（这里是跳跃表和红黑树）。

如果单纯比较性能，跳跃表和红黑树可以说相差不大，但是加上并发的环境就不一样了，如果要更新数据，跳跃表需要更新的部分就比较少，锁的东西也就比较少，所以不同线程争锁的代价就相对少了，而红黑树有个平衡的过程，牵涉到大量的节点，争锁的代价也就相对较高了。性能也就不如前者了。

B 树，B+ 树

它们特点是一样的，是多路查找树，一般用于数据库系统中，为什么，因为它们分支多层数少呗，都知道磁盘 IO 是非常耗时的，而像大量数据存储在磁盘中所以我们要有效的减少磁盘 IO 次数避免磁盘频繁的查找。

B+ 树是 B 树的变种树，有 n 棵子树的节点中含有 n 个关键字，每个关键字不保存数据，只用来索引，数据都保存在叶子节点。是为文件系统而生的。

Trie 树

又名单词查找树，一种树形结构，常用来操作字符串。它是不同字符串的相同前缀只保存一份。相对直接保存字符串肯定是节省空间的，但是它保存大量字符串时会很耗费内存（是内存）。类似的有前缀树 (prefix tree)，后缀树 (suffix tree)，radix tree(patricia tree, compact prefix tree)，crit-bit tree（解决耗费内存问题），以及前面说的 double array trie。

简单的补充下我了解应用

前缀树：字符串快速检索，字符串排序，最长公共前缀，自动匹配前缀显示后缀。
后缀树：查找字符串 s1 在 s2 中，字符串 s1 在 s2 中出现的次数，字符串 s1,s2 最长公共部分，最长回文串。
radix tree：linux 内核，nginx。

refs and see also

AVL 树，红黑树，B 树，B+ 树，Trie 树都分别应用在哪些现实场景中？ - 知乎

数据结构与算法中，树一般会应用在哪些方面？为什么？ @

树的一个大类是自平衡二叉搜索树 (self-balanced BST), 变种特别多:

RB 树是每个节点是红色或者黑色, 颜色隔代遗传
AVL 树是每个节点包含平衡因子, 等于左高-右高
Splay 树是每个节点带个父节点的指针
Treap 是每个节点都带个随机的 priority number, parent priority >= child priority

… (其实说白了都是为了方便平衡操作给节点附加一个字段)

自平衡二叉搜索树在面试中经常出现, 但做网页的互联网码农却很少用得上… 如果是当 Map 用, 往往还不如直接上哈希表. 如果是当排序用, 不如直接用排序算法… 不过也有有用的时候, 例如查找一个数字的上下界.

树的另一个大类是 Trie, 特点是能保证字典序, 存储词典的空间压缩率高, 能做前缀搜索. 在正则匹配, 数据压缩, 构建索引都可能用到. Trie 也有不少变种:

Double Array - trie 的一个经典实现 (这实现其实不算树, 也不适合处理非 ascii 字符的情况)
Patricia Trie (Radix-Tree) - 每个节点可以存一段字符串而不限于一个字符
Judy Array - 基于 256-ary radix tree, 用了 20 种压缩方式, 极其复杂…
Burst Trie - 如果一个子树足够小, 就用 binary 堆的方式存储, 不过压缩效果一般
HAT Trie - 压缩率高而且不容易出现 CPU cache miss, 查速接近哈希表而耗内存少得多. 节点可以是以下三种之一: Array Hash, 序列化的 Bucket, 传统 Trie node
MARISA Trie - 压缩率最高, 支持 mmap 载入, 也是用了很多压缩技巧的复杂实现, 就是构建比较花时间, 也不能动态更新

refs and see also

数据结构与算法中，树一般会应用在哪些方面？为什么？ - 知乎

用链表的目的是什么？省空间还是省时间？ @

链表的优点除了「插入删除不需要移动其他元素」之外，还在于它是一个局部化结构。就是说当你拿到链表的一个 node 之后，不需要太多其它数据，就可以完成插入，删除的操作。而其它的数据结构不行。比如说 array，你只拿到一个 item 是断不敢做插入删除的。

当然了，局部化这个好处只有 intrusive（侵入的；打扰的）链表才有，就是必须 prev/next 嵌入在数据结构中。像 STL 和 Java 那种设计是失败了。

refs and see also

用链表的目的是什么？省空间还是省时间？ - 知乎

Graph (abstract data type) @

In computer science, a graph is an abstract data type that is meant to implement the undirected graph and directed graph concepts from mathematics.

The basic operations provided by a graph data structure G usually include:

adjacent(G, x, y): tests whether there is an edge from the vertices x to y;
neighbors(G, x): lists all vertices y such that there is an edge from the vertices x to y;
add_vertex(G, x): adds the vertex x, if it is not there;
remove_vertex(G, x): removes the vertex x, if it is there;
add_edge(G, x, y): adds the edge from the vertices x to y, if it is not there;
remove_edge(G, x, y): removes the edge from the vertices x to y, if it is there;
get_vertex_value(G, x): returns the value associated with the vertex x;
set_vertex_value(G, x, v): sets the value associated with the vertex x to v.

Structures that associate values to the edges usually also provide:

get_edge_value(G, x, y): returns the value associated with the edge (x, y);
set_edge_value(G, x, y, v): sets the value associated with the edge (x, y) to v.

Adjacency List

Vertices are stored as records or objects, and every vertex stores a list of adjacent vertices. This data structure allows the storage of additional data on the vertices. Additional data can be stored if edges are also stored as objects, in which case each vertex stores its incident edges and each edge stores its incident vertices.

Adjancy Matrix

A two-dimensional matrix, in which the rows represent source vertices and columns represent destination vertices. Data on edges and vertices must be stored externally. Only the cost for one edge can be stored between each pair of vertices.

Incidence matrix

A two-dimensional Boolean matrix, in which the rows represent the vertices and columns represent the edges. The entries indicate whether the vertex at a row is incident to the edge at a column.

An undirected graph.

For example the incidence matrix of the undirected graph shown on the right is a matrix consisting of 4 rows (corresponding to the four vertices, 1-4) and 4 columns (corresponding to the four edges, e1-e4):

Adjacency lists are generally preferred because they efficiently represent sparse graphs. An adjacency matrix is preferred if the graph is dense, that is the number of edges |E| is close to the number of vertices squared, |V|², or if one must be able to quickly look up if there is an edge connecting two vertices.

refs and see also

trees @

Spanning tree @

In the mathematical field of graph theory, a spanning tree T of an undirected graph G is a subgraph that is a tree which includes all of the vertices of G. In general, a graph may have several spanning trees, but a graph that is not connected will not contain a spanning tree (but see Spanning forests below). If all of the edges of G are also edges of a spanning tree T of G, then G is a tree and is identical to T (that is, a tree has a unique spanning tree and it is itself).

Several pathfinding algorithms, including Dijkstra’s algorithm and the A* search algorithm, internally build a spanning tree as an intermediate step in solving the problem.

Definitions: A tree is a connected undirected graph with no cycles. It is a spanning tree of a graph G if it spans G (that is, it includes every vertex of G) and is a subgraph of G (every edge in the tree belongs to G). A spanning tree of a connected graph G can also be defined as a maximal set of edges of G that contains no cycle, or as a minimal set of edges that connect all vertices.

minimal/minimum spanning tree

In some cases, it is easy to calculate t(G) directly:

If G is itself a tree, then t(G) = 1.
When G is the cycle graph Cn with n vertices, then t(G) = n.
For a complete graph with n vertices, Cayley’s formula gives the number of spanning trees as nⁿ⁻².
If G is the complete bipartite graph K_p,q, then t(G) = p^q-1q^p-1.
For the n-dimensional hypercube graph…

arbitrary tree?

see Kirchhoff’s theorem - Wikipedia, the free encyclopedia.

Prim’s algorithm @: In computer science, Prim’s algorithm is a greedy algorithm that finds a minimum spanning tree for a weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. The algorithm operates by building this tree one vertex at a time, from an arbitrary starting vertex, at each step adding the cheapest possible connection from the tree to another vertex.

Self-balancing binary search tree @

In computer science, a self-balancing (or height-balanced) binary search tree is any node-based binary search tree that automatically keeps its height (maximal number of levels below the root) small in the face of arbitrary item insertions and deletions.

The red–black tree, which is a type of self-balancing binary search tree, was called symmetric binary B-tree and was renamed but can still be confused with the generic concept of self-balancing binary search tree because of the initials.

AVL tree @

d(height(left), height(right)) = { -1, 0, 1 }, left-heavy, right-heavy, balanced.

Splay tree @

A splay（展开） tree is a self-adjusting binary search tree with the additional property that recently accessed elements are quick to access again. It performs basic operations such as insertion, look-up and removal in O(log n) amortized time. For many sequences of non-random operations, splay trees perform better than other search trees, even when the specific pattern of the sequence is unknown. The splay tree was invented by Daniel Sleator and Robert Tarjan in 1985.

Advantages @

Good performance for a splay tree depends on the fact that it is self-optimizing, in that frequently accessed nodes will move nearer to the root where they can be accessed more quickly. The worst-case height—though unlikely—is O(n), with the average being O(log n). Having frequently used nodes near the root is an advantage for many practical applications (also see Locality of reference), and is particularly useful for implementing caches and garbage collection algorithms.

Locality of reference @

In computer science, locality of reference, also known as the principle of locality, is a term for the phenomenon in which the same values, or related storage locations, are frequently accessed, depending on the memory access pattern. There are two basic types of reference locality – temporal and spatial locality. Temporal locality refers to the reuse of specific data, and/or resources, within a relatively small time duration. Spatial locality refers to the use of data elements within relatively close storage locations. Sequential locality, a special case of spatial locality, occurs when data elements are arranged and accessed linearly, such as, traversing the elements in a one-dimensional array.

Locality is merely one type of predictable behavior that occurs in computer systems. Systems that exhibit strong locality of reference are great candidates for performance optimization through the use of techniques such as the caching, prefetching for memory and advanced branch predictors at the pipelining stage of processor core.

There are several different types of locality of reference:

Temporal locality
Spatial locality
Memory locality
Branch locality
Equidistant locality

refs and see also

Locality of reference - Wikipedia, the free encyclopedia

Advantages include:

Comparable performance: Average-case performance is as efficient as other trees.
Small memory footprint: Splay trees do not need to store any bookkeeping data.

Disadvantages @

The most significant disadvantage of splay trees is that the height of a splay tree can be linear. For example, this will be the case after accessing all n elements in non-decreasing order. Since the height of a tree corresponds to the worst-case access time, this means that the actual cost of an operation can be high. However the amortized access cost of this worst case is logarithmic, O(log n). Also, the expected access cost can be reduced to O(log n) by using a randomized variant.

The representation of splay trees can change even when they are accessed in a ‘read-only’ manner (i.e. by find operations). This complicates the use of such splay trees in a multi-threaded environment. Specifically, extra management is needed if multiple threads are allowed to perform find operations concurrently. This also makes them unsuitable for general use in purely functional programming, although they can be used in limited ways to implement priority queues even there.

zig

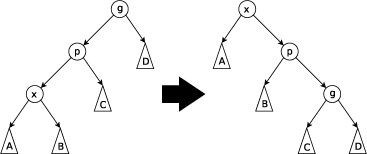
zig zig

C++ 实现 @

#include <functional>

#ifndef SPLAY_TREE
#define SPLAY_TREE

template< typename T, typename Comp = std::less< T > >
class splay_tree {
private:
  Comp comp;
  unsigned long p_size;

  struct node {
    node *left, *right;
    node *parent;
    T key;
    node( const T& init = T( ) ) : left( 0 ), right( 0 ), parent( 0 ), key( init ) { }
    ~node( ) {
      if( left ) delete left;
      if( right ) delete right;
      if( parent ) delete parent;
    }
  } *root;

  void left_rotate( node *x ) {
    node *y = x->right;
    if(y) {
      x->right = y->left;
      if( y->left ) y->left->parent = x;
      y->parent = x->parent;
    }

    if( !x->parent ) root = y;
    else if( x == x->parent->left ) x->parent->left = y;
    else x->parent->right = y;
    if(y) y->left = x;
    x->parent = y;
  }

  void right_rotate( node *x ) {
    node *y = x->left;
    if(y) {
      x->left = y->right;
      if( y->right ) y->right->parent = x;
      y->parent = x->parent;
    }
    if( !x->parent ) root = y;
    else if( x == x->parent->left ) x->parent->left = y;
    else x->parent->right = y;
    if(y) y->right = x;
    x->parent = y;
  }

  void splay( node *x ) {
    while( x->parent ) {
      if( !x->parent->parent ) {
        if( x->parent->left == x ) right_rotate( x->parent );
        else left_rotate( x->parent );
      } else if( x->parent->left == x && x->parent->parent->left == x->parent ) {
        right_rotate( x->parent->parent );
        right_rotate( x->parent );
      } else if( x->parent->right == x && x->parent->parent->right == x->parent ) {
        left_rotate( x->parent->parent );
        left_rotate( x->parent );
      } else if( x->parent->left == x && x->parent->parent->right == x->parent ) {
        right_rotate( x->parent );
        left_rotate( x->parent );
      } else {
        left_rotate( x->parent );
        right_rotate( x->parent );
      }
    }
  }

  void replace( node *u, node *v ) {
    if( !u->parent ) root = v;
    else if( u == u->parent->left ) u->parent->left = v;
    else u->parent->right = v;
    if( v ) v->parent = u->parent;
  }

  node* subtree_minimum( node *u ) {
    while( u->left ) u = u->left;
    return u;
  }

  node* subtree_maximum( node *u ) {
    while( u->right ) u = u->right;
    return u;
  }
public:
  splay_tree( ) : root( 0 ), p_size( 0 ) { }

  void insert( const T &key ) {
    node *z = root;
    node *p = 0;

    while( z ) {
      p = z;
      if( comp( z->key, key ) ) z = z->right;
      else z = z->left;
    }

    z = new node( key );
    z->parent = p;

    if( !p ) root = z;
    else if( comp( p->key, z->key ) ) p->right = z;
    else p->left = z;

    splay( z );
    p_size++;
  }

  node* find( const T &key ) {
    node *z = root;
    while( z ) {
      if( comp( z->key, key ) ) z = z->right;
      else if( comp( key, z->key ) ) z = z->left;
      else return z;
    }
    return 0;
  }

  void erase( const T &key ) {
    node *z = find( key );
    if( !z ) return;

    splay( z );

    if( !z->left ) replace( z, z->right );
    else if( !z->right ) replace( z, z->left );
    else {
      node *y = subtree_minimum( z->right );
      if( y->parent != z ) {
        replace( y, y->right );
        y->right = z->right;
        y->right->parent = y;
      }
      replace( z, y );
      y->left = z->left;
      y->left->parent = y;
    }

    delete z;
    p_size--;
  }

  const T& minimum( ) { return subtree_minimum( root )->key; }
  const T& maximum( ) { return subtree_maximum( root )->key; }

  bool empty( ) const { return root == 0; }
  unsigned long size( ) const { return p_size; }
};

#endif // SPLAY_TREE

B-tree @

In computer science, a B-tree is a self-balancing tree data structure that keeps data sorted and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree is a generalization of a binary search tree in that a node can have more than two children (Comer 1979, p. 123). Unlike self-balancing binary search trees, the B-tree is optimized for systems that read and write large blocks of data. B-trees are a good example of a data structure for external memory. It is commonly used in databases and filesystems.

multi-way search tree: A multiway tree is a tree that can have more than two children. A multiway tree of order m (or an m-way tree) is one in which a tree can have m children.

A B-tree (Bayer & McCreight 1972) of order 5 (Knuth 1998).

Etymology @

The origin of “B-tree” has never been explained by the authors. As we shall see, “balanced,” “broad,” or “bushy” might apply. Others suggest that the “B” stands for Boeing. Because of his contributions, however, it seems appropriate to think of B-trees as “Bayer”-trees. (Comer 1979, p. 123 footnote 1)

Advantages of B-tree usage for databases @

The B-tree uses all of the ideas described above. In particular, a B-tree:

keeps keys in sorted order for sequential traversing
uses a hierarchical index to minimize the number of disk reads
uses partially full blocks to speed insertions and deletions
keeps the index balanced with an elegant recursive algorithm

In addition, a B-tree minimizes waste by making sure the interior nodes are at least half full. A B-tree can handle an arbitrary number of insertions and deletions.

Disadvantages of B-trees @

maximum key length cannot be changed without completely rebuilding the database. This led to many database systems truncating full human names to 70 characters.

According to Knuth’s definition, a B-tree of order m is a tree which satisfies the following properties:

Every node has at most m children.
Every non-leaf node (except root) has at least ⌈m/2⌉ (ceil of m/2) children.
The root has at least two children if it is not a leaf node.
A non-leaf node with k children contains k−1 keys.
All leaves appear in the same level

It can be shown (by induction for example) that a B-tree of height h with all its nodes completely filled has n= mh+1−1 entries. Hence, the best case height of a B-tree is: log_mⁿ⁺¹.

(A B Tree insertion example with each iteration. The nodes of this B tree have at most 3 children (Knuth order 3).

Red–black tree @

A red–black tree is a kind of self-balancing binary search tree. Each node of the binary tree has an extra bit, and that bit is often interpreted as the color (red or black) of the node. These color bits are used to ensure the tree remains approximately balanced during insertions and deletions.

Balance is preserved by painting each node of the tree with one of two colors (typically called ‘red’ and ‘black’) in a way that satisfies certain properties, which collectively constrain how unbalanced the tree can become in the worst case. When the tree is modified, the new tree is subsequently rearranged and repainted to restore the coloring properties. The properties are designed in such a way that this rearranging and recoloring can be performed efficiently.

The balancing of the tree is not perfect, but it is good enough to allow it to guarantee searching in O(log n) time, where n is the total number of elements in the tree. The insertion and deletion operations, along with the tree rearrangement and recoloring, are also performed in O(log n) time.

Tracking the color of each node requires only 1 bit of information per node because there are only two colors. The tree does not contain any other data specific to its being a red–black tree so its memory footprint is almost identical to a classic (uncolored) binary search tree. In many cases the additional bit of information can be stored at no additional memory cost.

The leaf nodes of red–black trees do not contain data. These leaves need not be explicit in computer memory—a null child pointer can encode the fact that this child is a leaf—but it simplifies some algorithms for operating on red–black trees if the leaves really are explicit nodes. To save memory, sometimes a single sentinel node performs the role of all leaf nodes; all references from internal nodes to leaf nodes then point to the sentinel node.

An example of a red–black tree

properties

A node is either red or black.
The root is black. This rule is sometimes omitted. Since the root can always be changed from red to black, but not necessarily vice versa, this rule has little effect on analysis.
All leaves (NIL) are black.
If a node is red, then both its children are black.
Every path from a given node to any of its descendant NIL nodes contains the same number of black nodes. Some definitions: the number of black nodes from the root to a node is the node’s 【black depth; the uniform number of black nodes in all paths from root to the leaves is called the 【black-height】 of the red–black tree.

These constraints enforce a critical property of red–black trees: the path from the root to the farthest leaf is no more than twice as long as the path from the root to the nearest leaf. The result is that the tree is roughly height-balanced. Since operations such as inserting, deleting, and finding values require worst-case time proportional to the height of the tree, this theoretical upper bound on the height allows red–black trees to be efficient in the worst case, unlike ordinary binary search trees.

The same red–black tree as in the example above, seen as a B-tree.

The red–black tree is then structurally equivalent to a B-tree of order 4, with a minimum fill factor of 33% of values per cluster with a maximum capacity of 3 values.

This B-tree type is still more general than a red–black tree though, as it allows ambiguity in a red–black tree conversion—multiple red–black trees can be produced from an equivalent B-tree of order 4.

Insertion @

RB-tree properties:

property 3 (all leaves are black) always holds.
property 4 (both children of every red node are black) is threatened only by adding a red node, repainting a black node red, or a rotation.
property 5 (all paths from any given node to its leaf nodes contain the same number of black nodes) is threatened only by adding a black node, repainting a red node black (or vice versa), or a rotation.

N: 当前 node，P：parent node，G：grandparent node，U：uncle node。 @

struct node *grandparent(struct node *n)
{
    if ((n != NULL) && (n->parent != NULL))
        return n->parent->parent;
    else
        return NULL;
}

struct node *uncle(struct node *n)
{
    struct node *g = grandparent(n);
    if (g == NULL)
        return NULL; // No grandparent means no uncle
    if (n->parent == g->left)
        return g->right;
    else
        return g->left;
}

struct node *sibling(struct node *n)
{
    if ((n == NULL) || (n->parent == NULL))
        return NULL; // no parent means no sibling
    if (n == n->parent->left)
        return n->parent->right;
    else
        return n->parent->left;
}

There are several cases of red–black tree insertion to handle:

N is the root node, i.e., first node of red–black tree @

void insert_case1(struct node *n)
{
    if (n->parent == NULL)
        n->color = BLACK;
    else
        insert_case2(n);
}

P is black @
```
void insert_case2(struct node *n)
{
    if (n->parent->color == BLACK)
        return; /* Tree is still valid */
    else
        insert_case3(n);
}
```
The current node’s parent P is black, so property 4 (both children of every red node are black) is not invalidated. In this case, the tree is still valid. Property 5 (all paths from any given node to its leaf nodes contain the same number of black nodes) is not threatened, because the current node N has two black leaf children, but because N is red, the paths through each of its children have the same number of black nodes as the path through the leaf it replaced, which was black, and so this property remains satisfied.

Note: In the following cases it can be assumed that N has a grandparent node G, because its parent P is red, and if it were the root, it would be black. Thus, N also has an uncle node U, although it may be a leaf in cases 4 and 5.

P & U are red @

void insert_case3(struct node *n)
{
    struct node *u = uncle(n), *g;

    if ((u != NULL) && (u->color == RED)) {
        n->parent->color = BLACK;
        u->color = BLACK;
        g = grandparent(n);
        g->color = RED;
        insert_case1(g);
    } else {
        insert_case4(n);
    }
}

Note: In the remaining cases, it is assumed that the parent node P is the left child of its parent. If it is the right child, left and right should be reversed throughout cases 4 and 5. The code samples take care of this.

N is added to right of left child of grandparent, or N is added to left of right child of grandparent (P is red and U is black) @

void insert_case4(struct node *n)
{
    struct node *g = grandparent(n);

    if ((n == n->parent->right) && (n->parent == g->left)) {
        rotate_left(n->parent);

        /*
         * rotate_left can be the below because of already having *g =  grandparent(n)
         *
         * struct node *saved_p=g->left, *saved_left_n=n->left;
         * g->left=n;
         * n->left=saved_p;
         * saved_p->right=saved_left_n;
         *
         * and modify the parent's nodes properly
         */

        n = n->left;

    } else if ((n == n->parent->left) && (n->parent == g->right)) {
        rotate_right(n->parent);

        /*
         * rotate_right can be the below to take advantage of already having *g =  grandparent(n)
         *
         * struct node *saved_p=g->right, *saved_right_n=n->right;
         * g->right=n;
         * n->right=saved_p;
         * saved_p->left=saved_right_n;
         *
         */

        n = n->right;
    }
    insert_case5(n);
}

N is added to left of left child of grandparent, or N is added to right of right child of grandparent (P is red and U is black) @

void insert_case5(struct node *n)
{
    struct node *g = grandparent(n);

    n->parent->color = BLACK;
    g->color = RED;
    if (n == n->parent->left)
        rotate_right(g);
    else
        rotate_left(g);
}

Note that inserting is actually in-place, since all the calls above use tail recursion.

Removal :TODO: @

todo.

可靠性、稳定性

k-d tree @

In computer science, a k-d tree (short for k-dimensional tree) is a space-partitioning data structure for organizing points in a k-dimensional space. k-d trees are a useful data structure for several applications, such as searches involving a multidimensional search key (e.g. range searches and nearest neighbor searches). k-d trees are a special case of binary space partitioning trees.

A 3-dimensional k-d tree. The first split (the red vertical plane) cuts the root cell (white) into two subcells, each of which is then split (by the green horizontal planes) into two subcells. Finally, those four cells are split (by the four blue vertical planes) into two subcells. Since there is no more splitting, the final eight are called leaf cells.

The k-d tree is a binary tree in which every node is a k-dimensional point. Every non-leaf node can be thought of as implicitly generating a splitting hyperplane that divides the space into two parts, known as half-spaces. Points to the left of this hyperplane are represented by the left subtree of that node and points right of the hyperplane are represented by the right subtree. The hyperplane direction is chosen in the following way: every node in the tree is associated with one of the k-dimensions, with the hyperplane perpendicular to that dimension’s axis. So, for example, if for a particular split the “x” axis is chosen, all points in the subtree with a smaller “x” value than the node will appear in the left subtree and all points with larger “x” value will be in the right subtree. In such a case, the hyperplane would be set by the x-value of the point, and its normal would be the unit x-axis.

k-d tree decomposition for the point set (2,3), (5,4), (9,6), (4,7), (8,1), (7,2).

The resulting k-d tree.

refs and see also

Hash Function @

A hash function is any function that can be used to map data of arbitrary size to data of fixed size. The values returned by a hash function are called hash values, hash codes, hash sums, or simply hashes.

Perfect hashing: A hash function that is injective—that is, maps each valid input to a different hash value—is said to be perfect. With such a function one can directly locate the desired entry in a hash table, without any additional searching.

refs and see also

Hash function - Wikipedia, the free encyclopedia

Dijkstra’s algorithm @

Dijkstra’s algorithm is an algorithm for finding the shortest paths between nodes in a graph, which may represent, for example, road networks. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.

Dijkstra’s algorithm to find the shortest path between a and b. It picks the unvisited vertex with the lowest distance, calculates the distance through it to each unvisited neighbor, and updates the neighbor’s distance if smaller. Mark visited (set to red) when done with neighbors.

 1  function Dijkstra(Graph, source):
 2
 3      create vertex set Q
 4
 5      for each vertex v in Graph:             // Initialization
 6          dist[v] ← INFINITY                  // Unknown distance from source to v
 7          prev[v] ← UNDEFINED                 // Previous node in optimal path from source
 8          add v to Q                          // All nodes initially in Q (unvisited nodes)
 9
10      dist[source] ← 0                        // Distance from source to source
11
12      while Q is not empty:
13          u ← vertex in Q with min dist[u]    // Source node will be selected first
14          remove u from Q
15
16          for each neighbor v of u:           // where v is still in Q.
17              alt ← dist[u] + length(u, v)
18              if alt < dist[v]:               // A shorter path to v has been found
19                  dist[v] ← alt
20                  prev[v] ← u
21
22      return dist[], prev[]

If we are only interested in a shortest path between vertices source and target, we can terminate the search after line 13 if u = target. Now we can read the shortest path from source to target by reverse iteration:

 1  S ← empty sequence
 2  u ← target
 3  while prev[u] is defined:                  // Construct the shortest path with a stack S
 4      insert u at the beginning of S         // Push the vertex onto the stack
 5      u ← prev[u]                            // Traverse from target to source
 6  insert u at the beginning of S             // Push the source onto the stack

Using a priority queue

 1  function Dijkstra(Graph, source):
 2      dist[source] ← 0                                // Initialization
 3
 4      create vertex set Q
 5
 6      for each vertex v in Graph:
 7          if v ≠ source
 8              dist[v] ← INFINITY                      // Unknown distance from source to v
 9              prev[v] ← UNDEFINED                     // Predecessor of v
10
11         Q.add_with_priority(v, dist[v])
12
13
14      while Q is not empty:                           // The main loop
15          u ← Q.extract_min()                         // Remove and return best vertex
16          for each neighbor v of u:                   // only v that is still in Q
17              alt = dist[u] + length(u, v)
18              if alt < dist[v]
19                  dist[v] ← alt
20                  prev[v] ← u
21                  Q.decrease_priority(v, alt)
22
23     return dist[], prev[]

refs and see also

Dijkstra’s algorithm - Wikipedia, the free encyclopedia

A* search algorithm @

In computer science, A* (pronounced as “A star”) is a computer algorithm that is widely used in pathfinding and graph traversal, the process of plotting an efficiently traversable path between multiple points, called nodes. Noted for its performance and accuracy, it enjoys widespread use. However, in practical travel-routing systems, it is generally outperformed by algorithms which can pre-process the graph to attain better performance, although other work has found A* to be superior to other approaches.

A* achieves better performance by using heuristics to guide its search.

A* selects the path that minimizes: f(n) = g(n) + h(n), n: node, g: cost dist, h: heuristic dist.

Key: green: start; blue: goal; orange: visited

function A*(start, goal)
    // The set of nodes already evaluated.
    closedSet := {}
    // The set of currently discovered nodes still to be evaluated.
    // Initially, only the start node is known.
    openSet := {start}
    // For each node, which node it can most efficiently be reached from.
    // If a node can be reached from many nodes, cameFrom will eventually contain the
    // most efficient previous step.
    cameFrom := the empty map

    // For each node, the cost of getting from the start node to that node.
    gScore := map with default value of Infinity
    // The cost of going from start to start is zero.
    gScore[start] := 0
    // For each node, the total cost of getting from the start node to the goal
    // by passing by that node. That value is partly known, partly heuristic.
    fScore := map with default value of Infinity
    // For the first node, that value is completely heuristic.
    fScore[start] := heuristic_cost_estimate(start, goal)

    while openSet is not empty
        current := the node in openSet having the lowest fScore[] value
        if current = goal
            return reconstruct_path(cameFrom, current)

        openSet.Remove(current)
        closedSet.Add(current)
        for each neighbor of current
            if neighbor in closedSet
                continue        // Ignore the neighbor which is already evaluated.
            // The distance from start to a neighbor
            tentative_gScore := gScore[current] + dist_between(current, neighbor)
            if neighbor not in openSet  // Discover a new node
                openSet.Add(neighbor)
            else if tentative_gScore >= gScore[neighbor]
                continue        // This is not a better path.

            // This path is the best until now. Record it!
            cameFrom[neighbor] := current
            gScore[neighbor] := tentative_gScore
            fScore[neighbor] := gScore[neighbor] + heuristic_cost_estimate(neighbor, goal)

    return failure

function reconstruct_path(cameFrom, current)
    total_path := [current]
    while current in cameFrom.Keys:
        current := cameFrom[current]
        total_path.append(current)
    return total_path

refs and see also

A* search algorithm - Wikipedia, the free encyclopedia

Travelling salesman problem @

The travelling salesman problem (TSP) asks the following question: Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city? It is an NP-hard problem in combinatorial optimization, important in operations research and theoretical computer science.

Solution of a travelling salesman problem

TSP can be modelled as an undirected weighted graph, such that cities are the graph’s vertices, paths are the graph’s edges, and a path’s distance is the edge’s length. It is a minimization problem starting and finishing at a specified vertex after having visited each other vertex exactly once. Often, the model is a complete graph (i.e. each pair of vertices is connected by an edge). If no path exists between two cities, adding an arbitrarily long edge will complete the graph without affecting the optimal tour.

Exact algorithms: try all permutations (ordered combinations) -> brute force, O(n!)
Heuristic and approximation algorithms: NN 近邻法

refs and see also

Travelling salesman problem - Wikipedia, the free encyclopedia

Blog Posts @

C++ 实现的 B+ 树 @
refs and see also
- algorithm/bptree.c at master · ghostrong/algorithm

OJ 工具 @

getx.h

#include <iostream>
#include <string>

namespace oj {

using namespace std;

template<typename T>
T get(istream & is = cin) {
    T val;
    is >> val;
    return val;
}

}

link-list.h

template<typename T>
class LinkList {
public:
    T val;
    LinkList* next;
    LinkList(T _val = 0): val(_val), next(NULL) {}
};

template<typename T>
ostream& operator<<(ostream& o, LinkList<T>* head){
    while(head){
        o<<head->val;
        if(head->next) o<<"->";
        head = head->next;
    }
    return o;
}

pair.h

template<typename T1, class T2>
istream & operator>> (istream & is, pair<T1, T2>& p) {
    T1 k;
    T2 v;
    is >> k >> v;
    p.first = k;
    p.second = v;
    return is;
}

template<typename T1, typename T2>
ostream & operator<< (ostream & o, pair<T1, T2>& p) {
    return o << '<' << p.first << "," << p.second << '>';
}

set.h, map.h

#include<iostream>
#include<sstream>
#include <set>
#include <unordered_set>
using namespace std;

// set
template<typename T>
istream& operator>>(istream& is, set<T>& st){
    string s; getline(is, s);
    stringstream ss(s);
    T v;
    while(ss>>v){
        st.insert(v);
    }
    return is;
}
template<typename T>
ostream& operator<<(ostream& o, set<T>& st){
    size_t i = st.size() - 1;
    typename set<T>::iterator it;
    o<<"{";
    for(it = st.begin(); it != st.end(); ++it, --i){
        o<<*it;
        if(i) o<<',';
    }
    return o<<"}";
}

// map
template<typename T1, typename T2>
istream & operator>>(istream & is, map<T1, T2>& m) {
    string s;
    getline(is, s);
    stringstream ss(s);
    T1 k;
    T2 v;
    while(ss >> k >> v){
        m[k] = v;
    }
    return is;
}
template<typename T1, typename T2>
ostream& operator<<(ostream& o, const map<T1, T2>& c) {
    o << "{";
    for(auto pr : c) o << pr << ' ';
    return o << "\b}";
}

vector.h

template<typename T>
ostream & operator<< (ostream & o, const vector<T>& v){
    o << "[";
    for(int i=0; i<v.size(); ++i){
        o << v[i];
        if(i<v.size()-1) o<< ',';
    }
    return o << "]";
}

template<typename T>
istream & operator>>(istream & is, vector<T>& v){
    string s; getline(is, s);
    stringstream ss(s);
    T tmp;
    while(ss >> tmp){
        v.push_back(tmp);
    }
    return is;
}

refs and see also

oj.h/lib at master · harttle/oj.h

微软 2015 校园招聘 Dec2 #2 Have Lunch Together | 天码营 - 新一代技术学习服务平台
LeetCode：一些编程心得 @
LeetCode 对基础数据结构和基础算法是很好的训练和考查。

（1）涉及的重要数据结构：

数组（一维，多维），链表，栈，队列，二叉树，无向图，散列，。。。

（2）涉及的重要算法技术：

贪心，动态规划，分治（递归），回溯（剪枝），搜索（广搜，深搜），。。。

刷题后的一些体会（以下说法不绝对）：
- 1，一般来说，贪心的时间复杂度在 O(n)，空间复杂度是 O(1) 或 O(n) 。
- 2，动规需要记录表（标记数组），时间复杂度经常是 O(n²)，空间复杂度也通常是 O(n²) 。
- 3，回溯很常见，重点是确定何时找到一个解、何时退出、越界时如何处理；通常需要一个线性结构来保存前面的状态，以便回溯时使用。
- 4，如果贪心、动规等方法都行不通，通常就考虑搜索来解决。
- 5，线性时间复杂度一般通过贪心方法实现；有时候，需要借助 HASH 结构（如 unordered_map）。
- 6，利用好栈 (stack)！很多问题通过栈能够在 O(n) 时间内解决。
- 7，深度优先搜索一般是递归的，数据过大时，递归深度太大出现问题；广度优先搜索一般借助队列，一般不需要递归。
- 8，初始化数组时，memset(address, value, n_bytes) (包含在 cstring.h) 是针对“字节”赋值！所以除非是单字节元素，或者初值为 0 或者 -1，否则不要用 memset 初始化；使用 vector 比较方便。
- 9，必要时，使用 unordered_map, unordered_set 等 C++ 容器。
- 10，必要时，利用类变量简化传参。
- 11，动规的关键是找到转移方程；因此动规的子问题具有“累积”性质。
- 12，贪心不同于动规，贪心的子问题不是“累积性“，而是具有“决定性”。
- 13，写代码最重要的是思路清楚、可理解性，而不是纠结变量少、代码短等无关紧要的问题。
- 14，由于单链表只能从前向后遍历，因此操作时经常需要保存所关心结点的前趋结点。
- 15，处理链表要时刻注意检查空指针 NULL。
- 16，数组检索、定位快；链表插入、删除快（不需要移动数据）。
- 17，vector, string 的性质都倾向于数组；List 的性质倾向于链表。
- 18，二叉树问题的基础是遍历方法：前序 / 中序 / 后续，递归与非递归都很重要。
- 19，关于二叉树的问题，有些是自顶向下的；也有些是自底向上的，如检查平衡二叉树。通常这两类问题都可以通过递归、非递归两种方法解决。
- 20，二叉树非递归遍历：前序遍历最简单，当前结点没有左儿子时，栈顶就是下一个结点；中序遍历需要先将当前结点（顶点）入栈，当前结点没有左儿子时，访问栈顶，并且栈内结点的头一个非空右儿子是下一个结点；后序遍历最后访问根结点，所以，顶点不仅要入栈，而且要记录是否访问了它的右儿子，只有访问了顶点的右儿子之后才能访问它自己。
- 21，许多问题需要应用二叉树遍历方法，有些问题需要在结点入栈的同时保存当前状态（如求最长路径）。
- 22，二叉树 Level 遍历的本质是广度优先搜索，需要利用队列。
- 23，关于”图“，LeetCode 只有一道遍历题目，需要到其他地方补充一下。
- 24，有些方法虽然 AC 了，但并不一定是最优美的。
（未完待续）

补充：多看一些经典算法的思路，着重理解算法本质还是很有必要的。毕竟，数据结构+算法还是核心。
Solving Every Sudoku Puzzle @
```
 A1 A2 A3| A4 A5 A6| A7 A8 A9    4 . . |. . . |8 . 5     4 1 7 |3 6 9 |8 2 5
 B1 B2 B3| B4 B5 B6| B7 B8 B9    . 3 . |. . . |. . .     6 3 2 |1 5 8 |9 4 7
 C1 C2 C3| C4 C5 C6| C7 C8 C9    . . . |7 . . |. . .     9 5 8 |7 2 4 |3 1 6
---------+---------+---------    ------+------+------    ------+------+------
 D1 D2 D3| D4 D5 D6| D7 D8 D9    . 2 . |. . . |. 6 .     8 2 5 |4 3 7 |1 6 9
 E1 E2 E3| E4 E5 E6| E7 E8 E9    . . . |. 8 . |4 . .     7 9 1 |5 8 6 |4 3 2
 F1 F2 F3| F4 F5 F6| F7 F8 F9    . . . |. 1 . |. . .     3 4 6 |9 1 2 |7 5 8
---------+---------+---------    ------+------+------    ------+------+------
 G1 G2 G3| G4 G5 G6| G7 G8 G9    . . . |6 . 3 |. 7 .     2 8 9 |6 4 3 |5 7 1
 H1 H2 H3| H4 H5 H6| H7 H8 H9    5 . . |2 . . |. . .     5 7 3 |2 9 1 |6 8 4
 I1 I2 I3| I4 I5 I6| I7 I8 I9    1 . 4 |. . . |. . .     1 6 4 |8 7 5 |2 9 3
```
```
"4.....8.5.3..........7......2.....6.....8.4......1.......6.3.7.5..2.....1.4......"

"""
400000805
030000000
000700000
020000060
000080400
000010000
000603070
500200000
104000000"""

"""
4 . . |. . . |8 . 5
. 3 . |. . . |. . .
. . . |7 . . |. . .
------+------+------
. 2 . |. . . |. 6 .
. . . |. 8 . |4 . .
. . . |. 1 . |. . .
------+------+------
. . . |6 . 3 |. 7 .
5 . . |2 . . |. . .
1 . 4 |. . . |. . .
"""
```
Constraint Propagation @
The function parse_grid calls assign(values, s, d). We could implement this as values[s] = d, but we can do more than just that. Those with experience solving Sudoku puzzles know that there are two important strategies that we can use to make progress towards filling in all the squares:

If a square has only one possible value, then eliminate that value from the square’s peers.

If a unit has only one possible place for a value, then put the value there.

As an example of strategy (1) if we assign 7 to A1, yielding {‘A1’: ‘7’, ‘A2’:‘123456789’, …}, we see that A1 has only one value, and thus the 7 can be removed from its peer A2 (and all other peers), giving us {‘A1’: ‘7’, ‘A2’: ‘12345689’, …}. As an example of strategy (2), if it turns out that none of A3 through A9 has a 3 as a possible value, then the 3 must belong in A2, and we can update to {‘A1’: ‘7’, ‘A2’:‘3’, …}. These updates to A2 may in turn cause further updates to its peers, and the peers of those peers, and so on. This process is called constraint propagation.
Search @

What is the search algorithm? Simple: first make sure we haven’t already found a solution or a contradiction, and if not, choose one unfilled square and consider all its possible values. One at a time, try assigning the square each value, and searching from the resulting position. In other words, we search for a value d such that we can successfully search for a solution from the result of assigning square s to d. If the search leads to an failed position, go back and consider another value of d. This is a recursive search, and we call it a depth-first search because we (recursively) consider all possibilities under values[s] = d before we consider a different value for s.
refs and see also
- pauek/norvig-sudoku: Norvig’s Sudoku solver in C++
一道阿里笔试题，思路应该是怎样？ @
refs and see also
- The-Art-Of-Programming-By-July/02.09.md at master · julycoding/The-Art-Of-Programming-By-July
- 一道阿里笔试题，思路应该是怎样？ - 知乎
Algorithms, 4th Edition by Robert Sedgewick and Kevin Wayne @
essential information that every serious programmer needs to know about algorithms and data structures

refs and see also
- Algorithms, 4th Edition by Robert Sedgewick and Kevin Wayne
Leetcode: Palindrome Partitioning II - Avril - 博客园
huangz/note — huangz/note @
算术 — huangz/note @
幂次定律 —— Power Law — huangz/note @

如果某件事的发生频率和它的某个属性成幂关系，那么这个频率就可以称之为符合幂次定律。

幂次定律的表现是，少数几个事件的发生频率占了整个发生频率的大部分，而其余的大多数事件只占整个发生频率的一个小部分，如图：

In statistics, a power law is a functional relationship between two quantities, where a relative change in one quantity results in a proportional relative change in the other quantity, independent of the initial size of those quantities: one quantity varies as a power of another. For instance, considering the area of a square in terms of the length of its side, if the length is doubled, the area is multiplied by a factor of four.

refs and see also

Exponential backoff - Wikipedia, the free encyclopedia

指数补偿 —— Exponential backoff — huangz/note @

指数补偿指的是，在执行事件时，通过反馈，逐渐降低某个过程的速率，从而最终找到一个合适的速率（来处理事件）。

Exponential backoff is an algorithm that uses feedback to multiplicatively decrease the rate of some process, in order to gradually find an acceptable rate.

refs and see also

Exponential backoff - Wikipedia, the free encyclopedia

将字符串解释为数字 —— Parse string to number — huangz/note @

就是 atoi。
第一章：计算系统简介 — huangz/note ♥️

第 2 章：传输层：TCP 、 UDP 和 SCTP — huangz/note

《UNIX 环境高级编程》笔记 — huangz/note

SimonS’s Algo - 知乎专栏 @

分班问题算法求解——动态规划 - SimonS’s Algo - 知乎专栏

倒刷 LeetCode——Valid Number - SimonS’s Algo - 知乎专栏 @

使用确定有穷状态自动机 (DFA) 来解答此题必然是最优雅的，无论空间还是时间复杂度都有不错的表现。如果不熟悉 DFA 的话也没关系，可以把本文当作入门教程来看。

所谓“确定有穷状态”，必然需要我们自己动手构造出所有状态来，如下所示：

0 初始无输入或者只有 space 的状态
1 输入了数字之后的状态
2 前面无数字，只输入了 dot 的状态
3 输入了 +/- 状态
4 前面有数字和有 dot 的状态
5 ‘e’ or ’E’输入后的状态
6 输入 e 之后输入 +/- 的状态
7 输入 e 后输入数字的状态
8 前面有有效数输入之后，输入 space 的状态

在 9 种状态中，我们可以发现只有 1、4、7、8 四种状态是合法的，所以题目迎刃而解，只要挨个遍历字符，通过判断遍历到最后一个字符时的状态即可确定该字符串是否合法。

在编程中，我们可以简单地用一个邻接矩阵来存储上图转移关系，不了解的同学请恶补图论相关基础知识。

class Solution:
    # @param {string} s
    # @return {boolean}
    def isNumber(self, s):
        INVALID=0; SPACE=1; SIGN=2; DIGIT=3; DOT=4; EXPONENT=5;
        #0invalid,1space,2sign,3digit,4dot,5exponent,6num_inputs
        transitionTable=[[-1, 0, 3, 1, 2, -1],      #0 no input or just spaces
                         [-1, 8, -1, 1, 4, 5],      #1 input is digits
                         [-1, -1, -1, 4, -1, -1],   #2 no digits in front just Dot
                         [-1, -1, -1, 1, 2, -1],    #3 sign
                         [-1, 8, -1, 4, -1, 5],     #4 digits and dot in front
                         [-1, -1, 6, 7, -1, -1],    #5 input 'e' or 'E'
                         [-1, -1, -1, 7, -1, -1],   #6 after 'e' input sign
                         [-1, 8, -1, 7, -1, -1],    #7 after 'e' input digits
                         [-1, 8, -1, -1, -1, -1]]   #8 after valid input input space
         state = 0
         for c in s:
            inputtype = INVALID

            if c == ' ': inputtype = SPACE
            elif c == '-' or c == '+': inputtype = SIGN
            elif c.isdigit(): inputtype = DIGIT
            elif c == '.': inputtype = DOT
            elif c.upper() == 'E': inputtype = EXPONENT

            state = transitionTable[state][inputtype]
            if state == -1: return False
            return state == 1 or state == 4 or state == 7 or state == 8

科学松鼠会 » 遗传算法：内存中的进化 @
简单地说，遗传算法是一种解决问题的方法。它模拟大自然中种群在选择压力下的演化，从而得到问题的一个近似解。

其次，为了使扇贝的样子向Firefox图标靠近，我们要给它们加上一点选择压力，就是文章开头故事中提到的那个人的行动：在每一代把最不像Firefox的扇贝淘汰出去，同时也给新的个体留下生存的空间。怎么评价这个扇贝像不像Firefox呢？最直接的方法就是一个一个像素比较，颜色相差得越多就越不像。这个评价的函数叫做“适应函数”，它负责评价一个个体到底有多适应我们的要求。

好了，现在是万事俱备只欠东风了。定义好基因，写好繁衍、变异、评价适应性、淘汰和终止的代码之后，只需要随机产生一个适当大小的种群，然后让它这样一代代的繁衍、变异和淘汰下去，到最后终止我们就会获得一个惊喜的结果：（这回是完整的了，图片下的数字表示这个扇贝是第几代中最好的）

其实，通过微调参数和繁衍、变异、淘汰、终止的代码，我们有可能得到更有效的算法。遗传算法只是一个框架，里边具体内容可以根据实际问题进行调整，这也是它能在许多问题上派上用场的一个原因。像这样可以适应很多问题的算法还有模拟退火算法、粒子群算法、蚁群算法、禁忌搜索等等，统称为元启发式算法（Meta-heuristic algorithms）。

Metaheuristic :TODO: @

TODO

遗传算法模拟一个人工种群的进化过程，通过选择 (Selection)、交叉 (Crossover) 以及变异 (Mutation) 等机制，在每次迭代中都保留一组候选个体，重复此过程，种群经过若干代以后，理想情况下其适应度达到近似最优的状态。

refs and see also
如何用简单易懂的例子解释隐马尔可夫模型？ - 知乎
机器学习专家与统计学家观点上有哪些不同？ - 知乎
奇异值的物理意义是什么？ - 知乎 @

科学网—奇异值分解 (SVD) — 几何意义 - 余露的博文
Heap · Data Structure and Algorithm notes
《DPV – Algorithm》算法之美（Algorithms）书评 @
算法作为一门学问，有两条正交的线索。一个是算法处理的对象：数、矩阵、集合、串 (strings)、排列 (permutations)、图 (graphs)、表达式(formula)、分布(distributions)，等等。另一个是算法的设计思想：贪婪、分治、动态规划、线性规划、局部搜索 (local search)，等等。这两条线索几乎是相互独立的：同一个离散对象，例如图，稍有不同的问题，例如single-source shortest path 和all-pair shortest path，就可以用到不同的设计思想，如贪婪和动态规划；而完全不同的离散对象上的问题，例如排序和整数乘法，也许就会用到相同的思想，例如分治。

refs and see also
- 算法之美（Algorithms）书评
《The Algorithm Design Manual》 @

Skiena’s Audio Lectures

不愧对“手册”之名，即使通读过 CLRS 再读也有所收获（算法设计手册）书评
red-black tree @
refs and see also
sorting @
refs and see also
- 排序（一）归并、快排、优先队列等（图文详解） - 菜鸟的自留地 - 博客频道 - CSDN.NET
- 排序（二）键索引、桶排序、位示图、败者树等（图文详解–败者树） - 菜鸟的自留地 - 博客频道 - CSDN.NET

Code Reading @

4ker/Lua-Source-Internal: Lua source internal

libevent 源码深度剖析一 - sparkliang 的专栏 - 博客频道 - CSDN.NET

libevent 源码深度剖析二 - sparkliang 的专栏 - 博客频道 - CSDN.NET

daoluan/decode-memcached: memcached 源码剖析注释

Redis 设计与实现 — Redis 设计与实现 ♥️ @

What is Redis @

Redis 是一个开源的使用 ANSI C 语言编写、支持网络、可基于内存亦可持久化的日志型、Key-Value 数据库，并提供多种语言的 API。从 2010 年 3 月 15 日起，Redis 的开发工作由VMware 主持。从 2013 年 5 月开始，Redis 的开发由 Pivotal 赞助。

Redis 的优点如下：

丰富的数据结构和命令
默认就有持久化
事务
值有 512MB（memcached 最大是 1MB）

Memcached 的优点：

可以做集群

refs and see also

Redis 和 Memcached 各有什么优缺点，主要的应用场景是什么样的？ - 知乎

第一部分：数据结构与对象 @

简单动态字符串 @

Redis 没有直接使用 C 语言传统的字符串表示（以空字符结尾的字符数组，以下简称 C 字符串），而是自己构建了一种名为简单动态字符串（simple dynamic string，SDS）的抽象类型，并将 SDS 用作 Redis 的默认字符串表示。

struct sdshdr {
    // 记录 buf 数组中已使用字节的数量
    // 等于 SDS 所保存字符串的长度
    int len;

    // 记录 buf 数组中未使用字节的数量
    int free;

    // 字节数组，用于保存字符串
    char buf[];
};

C 字符串	SDS
获取字符串长度的复杂度为 O(N) 。 API 是不安全的，可能会造成缓冲区溢出。修改字符串长度 N 次必然需要执行 N 次内存重分配。只能保存文本数据。可以使用所有库中的函数。	获取字符串长度的复杂度为 O(1) 。 API 是安全的，不会造成缓冲区溢出。修改字符串长度 N 次最多需要执行 N 次内存重分配。可以保存文本或者二进制数据。可以使用一部分库中的函数。

Redis 只会使用 C 字符串作为字面量，在大多数情况下， Redis 使用 SDS （Simple Dynamic String，简单动态字符串）作为字符串表示。

比起 C 字符串， SDS 具有以下优点：

常数复杂度获取字符串长度。
杜绝缓冲区溢出。
减少修改字符串长度时所需的内存重分配次数。
二进制安全。
兼容部分 C 字符串函数。

refs and see also

Null-terminated string - Wikipedia, the free encyclopedia

链表 @

typedef struct list {
    // 表头节点
    listNode *head;

    // 表尾节点
    listNode *tail;

    // 链表所包含的节点数量
    unsigned long len;

    // 节点值复制函数
    void *(*dup)(void *ptr);

    // 节点值释放函数
    void (*free)(void *ptr);

    // 节点值对比函数
    int (*match)(void *ptr, void *key);
} list;

Redis 的链表实现的特性可以总结如下：

双端：链表节点带有 prev 和 next 指针，获取某个节点的前置节点和后置节点的复杂度都是 O(1) 。
无环：表头节点的 prev 指针和表尾节点的 next 指针都指向 NULL ， 对链表的访问以 NULL 为终点。
带表头指针和表尾指针：通过 list 结构的 head 指针和 tail 指针，程序获取链表的表头节点和表尾节点的复杂度为 O(1) 。
带链表长度计数器：程序使用 list 结构的 len 属性来对 list 持有的链表节点进行计数，程序获取链表中节点数量的复杂度为 O(1) 。
多态：链表节点使用 void* 指针来保存节点值，并且可以通过 list 结构的 dup 、 free 、 match 三个属性为节点值设置类型特定函数，所以链表可以用于保存各种不同类型的值。

重点回顾

链表被广泛用于实现 Redis 的各种功能，比如列表键，发布与订阅，慢查询，监视器，等等。
每个链表节点由一个 listNode 结构来表示，每个节点都有一个指向前置节点和后置节点的指针，所以 Redis 的链表实现是双端链表。
每个链表使用一个 list 结构来表示，这个结构带有表头节点指针、表尾节点指针、以及链表长度等信息。
因为链表表头节点的前置节点和表尾节点的后置节点都指向 NULL ，所以 Redis 的链表实现是无环链表。
通过为链表设置不同的类型特定函数， Redis 的链表可以用于保存各种不同类型的值。

字典 @

字典经常作为一种数据结构内置在很多高级编程语言里面，但 Redis 所使用的 C 语言并没有内置这种数据结构，因此 Redis 构建了自己的字典实现。

字典在 Redis 中的应用相当广泛，比如 Redis 的数据库就是使用字典来作为底层实现的，对数据库的增、删、查、改操作也是构建在对字典的操作之上的。

字典的实现 @

Redis 的字典使用哈希表作为底层实现，一个哈希表里面可以有多个哈希表节点，而每个哈希表节点就保存了字典中的一个键值对。

// key-value
typedef struct dictEntry {

    // 键
    void *key;

    // 值
    union {
        void *val;
        uint64_t u64;
        int64_t s64;
    } v;

    // 指向下个哈希表节点，形成链表
    struct dictEntry *next;

} dictEntry;

key 属性保存着键值对中的键，而 v 属性则保存着键值对中的值，其中键值对的值可以是一个指针，或者是一个 uint64_t 整数，又或者是一个 int64_t 整数。

next 属性是指向另一个哈希表节点的指针，这个指针可以将多个哈希值相同的键值对连接在一次，以此来解决键冲突（collision）的问题。

// dict hash table
typedef struct dictht {

    // 哈希表数组
    dictEntry **table;

    // 哈希表大小
    unsigned long size;

    // 哈希表大小掩码，用于计算索引值
    // 总是等于 size - 1
    unsigned long sizemask;

    // 该哈希表已有节点的数量
    unsigned long used;

} dictht;

// dict
typedef struct dict {

    // 类型特定函数
    dictType *type;

    // 私有数据
    void *privdata;

    // 哈希表
    dictht ht[2];

    // rehash 索引
    // 当 rehash 不在进行时，值为 -1
    int rehashidx; /* rehashing not in progress if rehashidx == -1 */

} dict;

typedef struct dictType {

    // 计算哈希值的函数
    unsigned int (*hashFunction)(const void *key);

    // 复制键的函数
    void *(*keyDup)(void *privdata, const void *key);

    // 复制值的函数
    void *(*valDup)(void *privdata, const void *obj);

    // 对比键的函数
    int (*keyCompare)(void *privdata, const void *key1, const void *key2);

    // 销毁键的函数
    void (*keyDestructor)(void *privdata, void *key);

    // 销毁值的函数
    void (*valDestructor)(void *privdata, void *obj);

} dictType;

哈希算法 @

# 使用字典设置的哈希函数，计算键 key 的哈希值
hash = dict->type->hashFunction(key);

# 使用哈希表的 sizemask 属性和哈希值，计算出索引值
# 根据情况不同， ht[x] 可以是 ht[0] 或者 ht[1]
index = hash & dict->ht[x].sizemask;

Redis 使用 MurmurHash2 算法来计算键的哈希值。

MurmurHash 算法最初由 Austin Appleby 于 2008 年发明，这种算法的优点在于，即使输入的键是有规律的，算法仍能给出一个很好的随机分布性，并且算法的计算速度也非常快。

解决键冲突 @

Redis 的哈希表使用链地址法（separate chaining）来解决键冲突：每个哈希表节点都有一个 next 指针，多个哈希表节点可以用 next 指针构成一个单向链表，被分配到同一个索引上的多个节点可以用这个单向链表连接起来，这就解决了键冲突的问题。

因为 dictEntry 节点组成的链表没有指向链表表尾的指针，所以为了速度考虑，程序总是将新节点添加到链表的表头位置（复杂度为 O(1)），排在其他已有节点的前面。

rehash @

before

“malloc” for ht[1]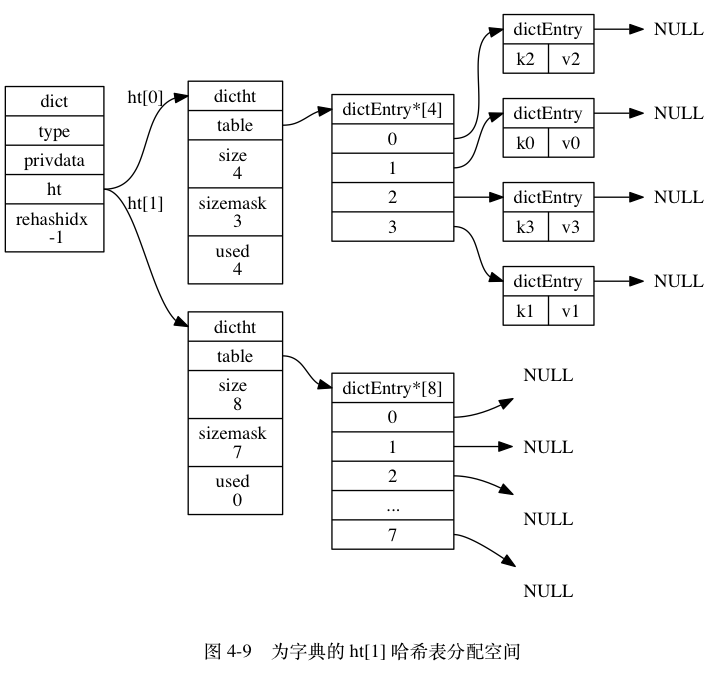

copy

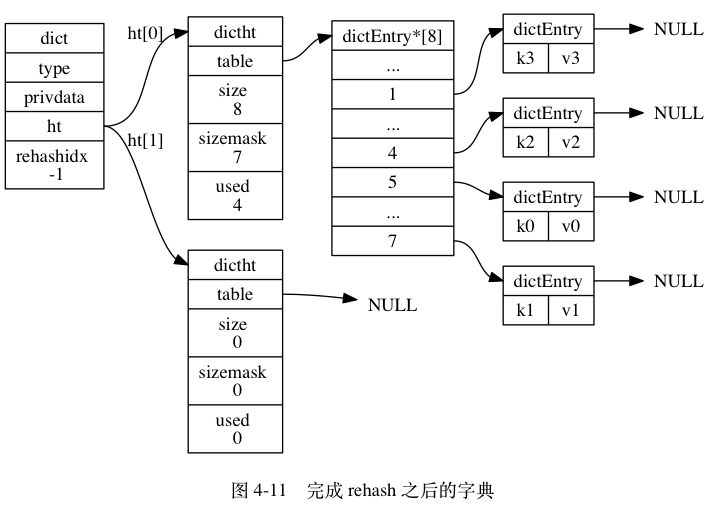
after

哈希表的扩展与收缩

当以下条件中的任意一个被满足时，程序会自动开始对哈希表执行扩展操作：

服务器目前没有在执行 BGSAVE 命令或者 BGREWRITEAOF 命令，并且哈希表的负载因子大于等于 1（因为是链式，所以 load factor 可以大于 1）；
服务器目前正在执行 BGSAVE 命令或者 BGREWRITEAOF 命令，并且哈希表的负载因子大于等于 5 ；

其中哈希表的负载因子可以通过公式：

# 负载因子 = 哈希表已保存节点数量 / 哈希表大小
load_factor = ht[0].used / ht[0].size

渐进式 rehash @

因此，为了避免 rehash 对服务器性能造成影响，服务器不是一次性将 ht[0] 里面的所有键值对全部 rehash 到 ht[1]，而是分多次、渐进式地将 ht[0] 里面的键值对慢慢地 rehash 到 ht[1]。

因为在进行渐进式 rehash 的过程中，字典会同时使用 ht[0] 和 ht[1] 两个哈希表，所以在渐进式 rehash 进行期间，字典的删除（delete）、查找（find）、更新（update）等操作会在两个哈希表上进行：比如说，要在字典里面查找一个键的话，程序会先在 ht[0] 里面进行查找，如果没找到的话，就会继续到 ht[1] 里面进行查找，诸如此类。

另外，在渐进式 rehash 执行期间，新添加到字典的键值对一律会被保存到 ht[1] 里面，而 ht[0] 则不再进行任何添加操作：这一措施保证了 ht[0] 包含的键值对数量会只减不增，并随着 rehash 操作的执行而最终变成空表。

重点回顾 @

字典被广泛用于实现 Redis 的各种功能，其中包括数据库和哈希键。
Redis 中的字典使用哈希表作为底层实现，每个字典带有两个哈希表，一个用于平时使用，另一个仅在进行 rehash 时使用。
当字典被用作数据库的底层实现，或者哈希键的底层实现时， Redis 使用 MurmurHash2 算法来计算键的哈希值。
哈希表使用链地址法来解决键冲突，被分配到同一个索引上的多个键值对会连接成一个单向链表。
在对哈希表进行扩展或者收缩操作时，程序需要将现有哈希表包含的所有键值对 rehash 到新哈希表里面，并且这个 rehash 过程并不是一次性地完成的，而是渐进式地完成的。

跳跃表 @

跳跃表（skiplist）是一种有序数据结构，它通过在每个节点中维持多个指向其他节点的指针，从而达到快速访问节点的目的。

跳跃表支持平均 O(log N) 最坏 O(N) 复杂度的节点查找，还可以通过顺序性操作来批量处理节点。

在大部分情况下，跳跃表的效率可以和平衡树相媲美，并且因为跳跃表的实现比平衡树要来得更为简单，所以有不少程序都使用跳跃表来代替平衡树。

Redis 使用跳跃表作为有序集合键的底层实现之一：如果一个有序集合包含的元素数量比较多，又或者有序集合中元素的成员（member）是比较长的字符串时， Redis 就会使用跳跃表来作为有序集合键的底层实现。

和链表、字典等数据结构被广泛地应用在 Redis 内部不同， Redis 只在两个地方用到了跳跃表，一个是实现有序集合键，另一个是在集群节点中用作内部数据结构，除此之外，跳跃表在 Redis 里面没有其他用途。

重点回顾 @

跳跃表是有序集合的底层实现之一，除此之外它在 Redis 中没有其他应用。
Redis 的跳跃表实现由 zskiplist 和 zskiplistNode 两个结构组成，其中 zskiplist 用于保存跳跃表信息（比如表头节点、表尾节点、长度），而 zskiplistNode 则用于表示跳跃表节点。
每个跳跃表节点的层高都是 1 至 32 之间的随机数。
在同一个跳跃表中，多个节点可以包含相同的分值，但每个节点的成员对象必须是唯一的。
跳跃表中的节点按照分值大小进行排序，当分值相同时，节点按照成员对象的大小进行排序。

整数集合 @

整数集合（intset）是集合键的底层实现之一：当一个集合只包含整数值元素，并且这个集合的元素数量不多时， Redis 就会使用整数集合作为集合键的底层实现。

typedef struct intset {

    // 编码方式
    uint32_t encoding;

    // 集合包含的元素数量
    uint32_t length;

    // 保存元素的数组
    int8_t contents[];

} intset;

每当我们要将一个新元素添加到整数集合里面，并且新元素的类型比整数集合现有所有元素的类型都要长时，整数集合需要先进行升级（upgrade），然后才能将新元素添加到整数集合里面。

升级整数集合并添加新元素共分为三步进行：

根据新元素的类型，扩展整数集合底层数组的空间大小，并为新元素分配空间。
将底层数组现有的所有元素都转换成与新元素相同的类型，并将类型转换后的元素放置到正确的位上，而且在放置元素的过程中，需要继续维持底层数组的有序性质不变。
将新元素添加到底层数组里面。

比如说，如果我们一直只向整数集合添加 int16_t 类型的值，那么整数集合的底层实现就会一直是 int16_t 类型的数组，只有在我们要将 int32_t 类型或者 int64_t 类型的值添加到集合时，程序才会对数组进行升级。

整数集合不支持降级操作，一旦对数组进行了升级，编码就会一直保持升级后的状态。

举个例子，对于图 6-11 所示的整数集合来说，即使我们将集合里唯一一个真正需要使用 int64_t 类型来保存的元素 4294967295 删除了，整数集合的编码仍然会维持 INTSET_ENC_INT64 ，底层数组也仍然会是 int64_t 类型的，

intsetNew           创建一个新的整数集合。  O(1)
intsetAdd           将给定元素添加到整数集合里面。  O(N)
intsetRemove        从整数集合中移除给定元素。  O(N)
intsetFind          检查给定值是否存在于集合。  因为底层数组有序，查找可以通过二分查找法来进行， 所以复杂度为 O(log N) 。
intsetRandom        从整数集合中随机返回一个元素。  O(1)
intsetGet           取出底层数组在给定索引上的元素。    O(1)
intsetLen           返回整数集合包含的元素个数。    O(1)
intsetBlobLen       返回整数集合占用的内存字节数。  O(1)

重点回顾

整数集合是集合键的底层实现之一。
整数集合的底层实现为数组，这个数组以有序、无重复的方式保存集合元素，在有需要时，程序会根据新添加元素的类型，改变这个数组的类型。
升级操作为整数集合带来了操作上的灵活性，并且尽可能地节约了内存。
整数集合只支持升级操作，不支持降级操作。

压缩列表 @

压缩列表（ziplist）是列表键和哈希键的底层实现之一。

当一个列表键只包含少量列表项，并且每个列表项要么就是小整数值，要么就是长度比较短的字符串，那么 Redis 就会使用压缩列表来做列表键的底层实现。

压缩列表的构成 @

压缩列表是 Redis 为了节约内存而开发的，由一系列特殊编码的连续内存块组成的顺序型（sequential）数据结构。

一个压缩列表可以包含任意多个节点（entry），每个节点可以保存一个字节数组或者一个整数值。

图 7-1 展示了压缩列表的各个组成部分，表 7-1 则记录了各个组成部分的类型、长度、以及用途。

每个压缩列表节点都由 previous_entry_length 、 encoding 、 content 三个部分组成，如图 7-4 所示。

压缩列表的从表尾向表头遍历操作就是使用这一原理实现的：只要我们拥有了一个指向某个节点起始地址的指针，那么通过这个指针以及这个节点的 previous_entry_length 属性，程序就可以一直向前一个节点回溯，最终到达压缩列表的表头节点。

连锁更新 @

因为连锁更新在最坏情况下需要对压缩列表执行 N 次空间重分配操作，而每次空间重分配的最坏复杂度为 O(N) ，所以连锁更新的最坏复杂度为 O(N^2) 。

要注意的是，尽管连锁更新的复杂度较高，但它真正造成性能问题的几率是很低的：

首先，压缩列表里要恰好有多个连续的、长度介于 250 字节至 253 字节之间的节点，连锁更新才有可能被引发，在实际中，这种情况并不多见；
其次，即使出现连锁更新，但只要被更新的节点数量不多，就不会对性能造成任何影响：比如说，对三五个节点进行连锁更新是绝对不会影响性能的；

因为以上原因， ziplistPush 等命令的平均复杂度仅为 O(N) ，在实际中，我们可以放心地使用这些函数，而不必担心连锁更新会影响压缩列表的性能。

重点回顾 @

压缩列表是一种为节约内存而开发的顺序型数据结构。
压缩列表被用作列表键和哈希键的底层实现之一。
压缩列表可以包含多个节点，每个节点可以保存一个字节数组或者整数值。
添加新节点到压缩列表，或者从压缩列表中删除节点，可能会引发连锁更新操作，但这种操作出现的几率并不高。

对象

第二部分：单机数据库的实现 @

数据库 @: 服务器中的数据库切换数据库数据库键空间设置键的生存时间或过期时间过期键删除策略 Redis 的过期键删除策略 AOF 、RDB 和复制功能对过期键的处理数据库通知重点回顾
RDB 持久化 @: RDB 文件的创建与载入自动间隔性保存 RDB 文件结构分析 RDB 文件重点回顾
AOF 持久化 @: AOF 持久化的实现 AOF 文件的载入与数据还原 AOF 重写重点回顾
事件 @: 文件事件时间事件事件的调度与执行重点回顾参考资料
客户端 @: 客户端属性客户端的创建与关闭重点回顾
服务器 @: 命令请求的执行过程 serverCron 函数初始化服务器重点回顾

第三部分：多机数据库的实现 @

复制 @: 旧版复制功能的实现旧版复制功能的缺陷新版复制功能的实现部分重同步的实现 PSYNC 命令的实现复制的实现心跳检测重点回顾
Sentinel @: 启动并初始化 Sentinel 获取主服务器信息获取从服务器信息向主服务器和从服务器发送信息接收来自主服务器和从服务器的频道信息检测主观下线状态检查客观下线状态选举领头 Sentinel 故障转移重点回顾参考资料
集群 @: 节点槽指派在集群中执行命令重新分片 ASK 错误复制与故障转移消息重点回顾

第四部分：独立功能的实现 @

发布与订阅 @: 频道的订阅与退订模式的订阅与退订发送消息查看订阅信息重点回顾参考资料
事务 @: 事务的实现 WATCH 命令的实现事务的 ACID 性质重点回顾参考资料
Lua 脚本 @: 创建并修改 Lua 环境 Lua 环境协作组件 EVAL 命令的实现 EVALSHA 命令的实现脚本管理命令的实现脚本复制重点回顾参考资料
排序 @: SORT 命令的实现 ALPHA 选项的实现 ASC 选项和 DESC 选项的实现 BY 选项的实现带有 ALPHA 选项的 BY 选项的实现 LIMIT 选项的实现 GET 选项的实现 STORE 选项的实现多个选项的执行顺序重点回顾
二进制位数组 @: 位数组的表示 GETBIT 命令的实现 SETBIT 命令的实现 BITCOUNT 命令的实现 BITOP 命令的实现重点回顾参考资料
慢查询日志 @: 慢查询记录的保存慢查询日志的阅览和删除添加新日志重点回顾
监视器 @: 成为监视器向监视器发送命令信息重点回顾

LeetCode 题目总结/分类 @
注：此分类仅供大概参考，没有精雕细琢。有不同意见欢迎评论~ 欢迎参考我的leetcode代码

利用堆栈：
- http://oj.leetcode.com/problems/evaluate-reverse-polish-notation/
- http://oj.leetcode.com/problems/longest-valid-parentheses/ （也可以用一维数组，贪心）
- http://oj.leetcode.com/problems/valid-parentheses/
- http://oj.leetcode.com/problems/largest-rectangle-in-histogram/
- 特别注意细节：http://oj.leetcode.com/problems/trapping-rain-water/
多种数据结构：
- http://oj.leetcode.com/problems/lru-cache/
- http://oj.leetcode.com/problems/substring-with-concatenation-of-all-words/ (注意遍历方法）
- HASH：http://oj.leetcode.com/problems/longest-consecutive-sequence/
简单编程：
- http://oj.leetcode.com/problems/longest-common-prefix/
- http://oj.leetcode.com/problems/string-to-integer-atoi/ (分析，控制语句）
排序 & 查找：
- 二分查找：http://oj.leetcode.com/problems/search-a-2d-matrix/
- 二分查找进阶：http://oj.leetcode.com/problems/search-for-a-range/
- 二分查找应用：http://oj.leetcode.com/problems/sqrtx/
- 二分查找应用：http://oj.leetcode.com/problems/search-insert-position/
- 二分查找变种：http://oj.leetcode.com/problems/search-in-rotated-sorted-array/
- 二分查找变种：http://oj.leetcode.com/problems/search-in-rotated-sorted-array-ii/
简单数学：
- http://oj.leetcode.com/problems/pascals-triangle/
- http://oj.leetcode.com/problems/pascals-triangle-ii/
- http://oj.leetcode.com/problems/powx-n/
- http://oj.leetcode.com/problems/reverse-integer/
- http://oj.leetcode.com/problems/plus-one/
- http://oj.leetcode.com/problems/unique-paths/
- http://oj.leetcode.com/problems/palindrome-number/
- http://oj.leetcode.com/problems/permutation-sequence/
- http://oj.leetcode.com/problems/merge-intervals/
- http://oj.leetcode.com/problems/valid-number/
- http://oj.leetcode.com/problems/climbing-stairs/
- http://oj.leetcode.com/problems/roman-to-integer/
- http://oj.leetcode.com/problems/integer-to-roman/
- http://oj.leetcode.com/problems/divide-two-integers/
- 区间：http://oj.leetcode.com/problems/insert-interval/
大数的数学运算：
- http://oj.leetcode.com/problems/add-binary/
- http://oj.leetcode.com/problems/add-two-numbers/
数组：
- http://oj.leetcode.com/problems/remove-element/
- http://oj.leetcode.com/problems/merge-sorted-array/
- http://oj.leetcode.com/problems/first-missing-positive/
- http://oj.leetcode.com/problems/spiral-matrix/
- http://oj.leetcode.com/problems/spiral-matrix-ii/
- http://oj.leetcode.com/problems/rotate-image/
- 遍历技巧：http://oj.leetcode.com/problems/container-with-most-water/
- http://oj.leetcode.com/problems/two-sum/
- http://oj.leetcode.com/problems/3sum/
- http://oj.leetcode.com/problems/3sum-closest/
- http://oj.leetcode.com/problems/4sum/
- http://oj.leetcode.com/problems/set-matrix-zeroes/
- 用好标记数组：http://oj.leetcode.com/problems/valid-sudoku/
- http://oj.leetcode.com/problems/next-permutation/
- http://oj.leetcode.com/problems/word-search/
- http://oj.leetcode.com/problems/remove-duplicates-from-sorted-array/
- http://oj.leetcode.com/problems/remove-duplicates-from-sorted-array-ii/
- http://oj.leetcode.com/problems/sort-colors/
暴力方法/细节实现：
- http://oj.leetcode.com/problems/max-points-on-a-line/
链表：
- 归并排序：http://oj.leetcode.com/problems/sort-list/
- 插入排序：http://oj.leetcode.com/problems/insertion-sort-list/
- 反转、插入：http://oj.leetcode.com/problems/reorder-list/
- 检测是否有环：http://oj.leetcode.com/problems/linked-list-cycle/
- 确定链表环的起点：http://oj.leetcode.com/problems/linked-list-cycle-ii/
- Deep Copy 带有随机指针的链表：http://oj.leetcode.com/problems/copy-list-with-random-pointer/
- 链表细节：http://oj.leetcode.com/problems/rotate-list/
- http://oj.leetcode.com/problems/remove-duplicates-from-sorted-list/
- 删除细节：http://oj.leetcode.com/problems/remove-duplicates-from-sorted-list-ii/
- http://oj.leetcode.com/problems/partition-list/
- http://oj.leetcode.com/problems/swap-nodes-in-pairs/
- Merge 两个链表：http://oj.leetcode.com/problems/merge-two-sorted-lists/
- Merge 多链表：http://oj.leetcode.com/problems/merge-k-sorted-lists/
- 细节：http://oj.leetcode.com/problems/reverse-nodes-in-k-group/
- http://oj.leetcode.com/problems/remove-nth-node-from-end-of-list/
- http://oj.leetcode.com/problems/reverse-linked-list-ii/
二叉树遍历：递归 & 非递归
- http://oj.leetcode.com/problems/same-tree/
- 前序：http://oj.leetcode.com/problems/binary-tree-preorder-traversal/
- 中序：http://oj.leetcode.com/problems/binary-tree-inorder-traversal/
- 后序：http://oj.leetcode.com/problems/binary-tree-postorder-traversal/
- 遍历变种：http://oj.leetcode.com/problems/sum-root-to-leaf-numbers/
- 遍历变种：http://oj.leetcode.com/problems/path-sum/
- 遍历变种：http://oj.leetcode.com/problems/path-sum-ii/
- 遍历变种：http://oj.leetcode.com/problems/maximum-depth-of-binary-tree/
- 遍历变种：http://oj.leetcode.com/problems/minimum-depth-of-binary-tree/
- 重建二叉树：http://oj.leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
- 重建二叉树：http://oj.leetcode.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/
- 层次遍历变种：http://oj.leetcode.com/problems/binary-tree-zigzag-level-order-traversal/
- 遍历变种：http://oj.leetcode.com/problems/symmetric-tree/
- 遍历应用：http://oj.leetcode.com/problems/binary-tree-maximum-path-sum/
- 遍历应用：http://oj.leetcode.com/problems/balanced-binary-tree/
- 遍历应用：http://oj.leetcode.com/problems/recover-binary-search-tree/
- 遍历应用：http://oj.leetcode.com/problems/flatten-binary-tree-to-linked-list/
- level遍历：http://oj.leetcode.com/problems/binary-tree-level-order-traversal/
- level 遍历：http://oj.leetcode.com/problems/binary-tree-level-order-traversal-ii/
- level 遍历变种：http://oj.leetcode.com/problems/populating-next-right-pointers-in-each-node/
- level 遍历变种：http://oj.leetcode.com/problems/populating-next-right-pointers-in-each-node-ii/
问题分析/智商/细节：
- http://oj.leetcode.com/problems/single-number/
- http://oj.leetcode.com/problems/single-number-ii/
- http://oj.leetcode.com/problems/candy/ ？
- http://oj.leetcode.com/problems/gas-station/
动态规划：
- http://oj.leetcode.com/problems/triangle/ （最短路径）
- http://oj.leetcode.com/problems/subsets/ （另一种形式）
- http://oj.leetcode.com/problems/subsets-ii/
- http://oj.leetcode.com/problems/edit-distance/ （经典）
- http://oj.leetcode.com/problems/word-break/
- http://oj.leetcode.com/problems/word-break-ii/
- http://oj.leetcode.com/problems/unique-binary-search-trees/ （动态规划避免递归）
- http://oj.leetcode.com/problems/unique-paths-ii/
- http://oj.leetcode.com/problems/scramble-string/
- http://oj.leetcode.com/problems/palindrome-partitioning/
- http://oj.leetcode.com/problems/palindrome-partitioning-ii/
- http://oj.leetcode.com/problems/interleaving-string/
- http://oj.leetcode.com/problems/distinct-subsequences/
- http://oj.leetcode.com/problems/decode-ways/
- http://oj.leetcode.com/problems/gray-code/
- http://oj.leetcode.com/problems/minimum-path-sum/
回溯：
- http://oj.leetcode.com/problems/combinations/
- http://oj.leetcode.com/problems/generate-parentheses/
- http://oj.leetcode.com/problems/combination-sum/
- http://oj.leetcode.com/problems/combination-sum-ii/
- http://oj.leetcode.com/problems/sudoku-solver/
- 经典N皇后：http://oj.leetcode.com/problems/n-queens/
- http://oj.leetcode.com/problems/n-queens-ii/
- http://oj.leetcode.com/problems/letter-combinations-of-a-phone-number/
贪心：
- http://oj.leetcode.com/problems/best-time-to-buy-and-sell-stock/
- http://oj.leetcode.com/problems/jump-game/
- http://oj.leetcode.com/problems/jump-game-ii/
- http://oj.leetcode.com/problems/best-time-to-buy-and-sell-stock-ii/
- http://oj.leetcode.com/problems/best-time-to-buy-and-sell-stock-iii/
- http://oj.leetcode.com/problems/maximum-subarray/
- http://oj.leetcode.com/problems/minimum-window-substring/
- http://oj.leetcode.com/problems/maximal-rectangle/
- http://oj.leetcode.com/problems/longest-substring-without-repeating-characters/
分治 & 递归：
- http://oj.leetcode.com/problems/unique-binary-search-trees-ii/
- http://oj.leetcode.com/problems/restore-ip-addresses/ （时间复杂度有限，递归满足）
- http://oj.leetcode.com/problems/permutations/
- http://oj.leetcode.com/problems/permutations-ii/
- http://oj.leetcode.com/problems/convert-sorted-array-to-binary-search-tree/
- http://oj.leetcode.com/problems/convert-sorted-list-to-binary-search-tree/
- http://oj.leetcode.com/problems/median-of-two-sorted-arrays/
- http://oj.leetcode.com/problems/validate-binary-search-tree/
字符串：
- http://oj.leetcode.com/problems/count-and-say/
- http://oj.leetcode.com/problems/implement-strstr/ （子串查找）
- http://oj.leetcode.com/problems/anagrams/
- http://oj.leetcode.com/problems/text-justification/ (细节）
- http://oj.leetcode.com/problems/simplify-path/ （基础控制语句 if-else-for）
- http://oj.leetcode.com/problems/multiply-strings/
- http://oj.leetcode.com/problems/regular-expression-matching/
- http://oj.leetcode.com/problems/wildcard-matching/
- http://oj.leetcode.com/problems/longest-palindromic-substring/
- http://oj.leetcode.com/problems/zigzag-conversion/
- http://oj.leetcode.com/problems/length-of-last-word/
- http://oj.leetcode.com/problems/valid-palindrome/
图：
- 深搜/广搜：http://oj.leetcode.com/problems/clone-graph/
搜索 & 遍历：
- http://oj.leetcode.com/problems/word-ladder/
- http://oj.leetcode.com/problems/word-ladder-ii/
- 广搜：http://oj.leetcode.com/problems/surrounded-regions/
refs and see also
- LeetCode 题目总结/分类

利用 Trie 树求多个字符串的最小编辑距离 @

编辑距离 @

1965 年，俄国科学家 Vladimir Levenshtein 给字符串相似度做出了一个明确的定义叫做 Levenshtein 距离，我们通常叫它“编辑距离”。字符串 A 到 B 的编辑距离是指，只用插入、删除和替换三种操作，最少需要多少步可以把 A 变成 B。例如，从 FAME 到 GATE 需要两步（两次替换），从 GAME 到 ACM 则需要三步（删除 G 和 E 再添加 C）。Levenshtein 给出了编辑距离的一般求法，就是大家都非常熟悉的经典动态规划问题。

Levenshtein 的定义可以是单词任意位置上的操作，似乎不遍历字典是不可能完成的。现在很多软件都有拼写检查的功能，提出更正建议的速度是很快的。它们到底是怎么做的呢？1973 年，Burkhard 和 Keller 提出的 BK 树有效地解决了这个问题。这个数据结构强就强在，它初步解决了一个看似不可能的问题，而其原理非常简单。

首先，我们观察 Levenshtein 距离的性质。令 d(x,y) 表示字符串 x 到 y 的 Levenshtein 距离，那么显然：

d(x,y) = 0 当且仅当 x=y （Levenshtein 距离为 0 <==> 字符串相等）
d(x,y) = d(y,x) （从 x 变到 y 的最少步数就是从 y 变到 x 的最少步数）
d(x,y) + d(y,z) >= d(x,z) （从 x 变到 z 所需的步数不会超过 x 先变成 y 再变成 z 的步数）

最后这一个性质叫做三角形不等式。就好像一个三角形一样，两边之和必然大于第三边。给某个集合内的元素定义一个二元的“距离函数”，如果这个距离函数同时满足上面说的三个性质，我们就称它为“度量空间”。我们的三维空间就是一个典型的度量空间，它的距离函数就是点对的直线距离。度量空间还有很多，比如 Manhattan 距离，图论中的最短路，当然还有这里提到的 Levenshtein 距离。就好像并查集对所有等价关系都适用一样，BK 树可以用于任何一个度量空间。

查询操作异常方便。如果我们需要返回与错误单词距离不超过 n 的单词，这个错误单词与树根所对应的单词距离为 d，那么接下来我们只需要递归地考虑编号在 d-n 到 d+n 范围内的边所连接的子树。由于 n 通常很小，因此每次与某个节点进行比较时都可以排除很多子树。

举个例子，假如我们输入一个 GAIE，程序发现它不在字典中。现在，我们想返回字典中所有与 GAIE 距离为 1 的单词。我们首先将 GAIE 与树根进行比较，得到的距离 d=1。由于 Levenshtein 距离满足三角形不等式，因此现在所有离 GAME 距离超过 2 的单词全部可以排除了。比如，以 AIM 为根的子树到 GAME 的距离都是 3，而 GAME 和 GAIE 之间的距离是 1，那么 AIM 及其子树到 GAIE 的距离至少都是 2。于是，现在程序只需要沿着标号范围在 1-1 到 1+1 里的边继续走下去。我们继续计算 GAIE 和 FAME 的距离，发现它为 2，于是继续沿标号在 1 和 3 之间的边前进。遍历结束后回到 GAME 的第二个节点，发现 GAIE 和 GAIN 距离为 1，输出 GAIN 并继续沿编号为 1 或 2 的边递归下去（那条编号为 4 的边连接的子树又被排除掉了）……

实践表明，一次查询所遍历的节点不会超过所有节点的 5% 到 8%，两次查询则一般不会 17-25%，效率远远超过暴力枚举。适当进行缓存，减小 Levenshtein 距离常数 n 可以使算法效率更高。

这篇文章真是够了，和 Matrix67 的几乎一模一样：字符串相似度之美（一）- SimonS’s Algo - 知乎专栏。

Trie 树的实现 @

由于多叉树不够灵活，同时对空间存在即大的浪费，因此本文利用二叉树实现一棵 Trie 树。

二叉树是这样的结构：节点的左孩子代表它的第一个孩子，节点的右孩子代表它的兄弟节点。

总体的思路是：

建立 10 万次的词典，单词长度 5-30
为这些单词建立 Trie 树，给定任意字符串，求所有与该字符串的编辑距离为 1 或者 2 的单词
同时用暴力匹配的方法求得符合要求的字符串，然后进行时间的比较。

#include <fstream>
#include <iostream>
#include <string>
#include <cstring>
#include <vector>
#include <algorithm>
#include <ctime>
#include <cstdlib>
#include <sys/time.h>

using namespace std;

const int X = 30;
const int Y = 30;
const int MAX = 30;

int edit_length(string &x, string &y);

// Trie树的节点定义
struct Node {
    int length;
    string word;
    Node *left, *right;
    Node() : length(0), word(""), left(0), right(0) { }
};

// Trie 树的操作定义
class Trie {
    private:
        Node* pRoot;
    private:
        // 销毁 Trie 树
        void destory(Node* r) {
            if(!r) { return; }
            destory(r -> left);
            destory(r -> right);
            delete r;
            r = NULL;
        }
        void find( Node *pRoot, string &str, int limit_num, vector<string> &word_set );
    public:
        Trie() {}
        ~Trie() { destroy(pRoot); }
        void insert(string str);
        void search(string &str, int limit_num, vector<string> &word_set);
};

// 插入单词，建立 Trie 树
void Trie::insert(string str){
    if(pRoot != NULL){
        //如果trie树已经存在
        Node *pPre = pRoot;
        Node *pCur = pRoot -> left;
        while(1) {
            //计算该单词与当前节点的编辑距离
            string word = pPre -> word;
            int distance = edit_length(word, str);
            //若该单词已存在
            if(distance == 0) {
                break;
            }
            //若该单词不存在
            if(pCur == NULL) {
                //若首节点不存在，则创建首节点
                pCur = new Node();
                pCur -> length = distance;
                pCur -> word = str;
                pCur -> left = NULL;
                pCur -> right = NULL;

                pPre -> left = pCur;

                break;

            } else if (pCur != NULL && pCur -> length > distance) {
                //若首节点存在，并且首节点大于目标编辑距离，重建首节点
                Node *p = new Node();
                p -> length = distance;
                p -> word = str;
                p -> left = NULL;
                p -> right = pCur;

                pPre -> left = p;
                break;

            } else {
                //首节点存在，且首节点小于等于目标编辑距离
                while(pCur != NULL && pCur -> length < distance){
                    pPre = pCur;
                    pCur = pCur -> right;
                }
                if(pCur != NULL && pCur -> length == distance){
                    //找到了目标节点
                    pPre = pCur;
                    pCur = pCur -> left;
                } else {
                    //创建目标节点
                    Node *p = new Node();
                    p -> length = distance;
                    p -> word = str;
                    p -> left = NULL;
                    p -> right = pCur;

                    pPre -> right = p;
                    break;
                }
            }
        }
    } else {
        //如果Trie树还不存在，以该单词创建根节点
        pRoot = new Node();
        pRoot -> length = 0;
        pRoot -> word = str;
    }
}

// 搜索与给定字符串的编辑距离小于给定值的所有字符串（内部调用）
void Trie::find(Node* pRoot, string &str, int limit_num, vector<string> &word_set) {

    if(pRoot == NULL){
        cout << "kong" << endl;
        return;
    }
    string word = pRoot -> word;
    int distance = edit_length(word, str);
    if(distance < limit_num) {
        word_set.push_back(word);
    }

    //如果当前节点有孩子的话
    Node *pCur = pRoot -> left;
    while(pCur != NULL){
        if(pCur -> length < distance + limit_num &&
                pCur -> length > distance - limit_num &&
                pCur -> length > limit_num - distance){
            find(pCur, str, limit_num, word_set);
        }
        pCur = pCur -> right;
    }
}


// 包装函数，搜索与给定字符串的编辑距离小于给定值的所有字符串（外部调用）
void Trie::search(string &str, int limit_num, vector<string> &word_set){
    find(pRoot, str, limit_num, word_set);
}

// ---------------------------工具函数------------------------------
// 求两个字符串的最断编辑距离
int edit_length(string &x, string &y){
    int xlen = x.length();
    int ylen = y.length();
    int edit[3][Y+1];
    memset(edit, 0, sizeof(edit));

    int i = 0;
    int j = 0;
    for(j = 0; j <= ylen; j++){
        edit[0][j] = j;
    }
    for(i = 1; i <= xlen; i++){
        edit[i%3][0] = edit[(i-1)%3][0] + 1;
        for(j = 1; j <= ylen; j++){
            if (x[i-1] == y[j-1]) {
                edit[i%3][j] = min(min(edit[i%3][j-1] + 1, edit[(i-1)%3][j] + 1),
                        edit[(i-1)%3][j-1]);
            } else {
                if(i >= 2 && j >= 2 && x[i-2] == y[j-1] && x[i-1] == y[j-2]){
                    edit[i%3][j] = min(min(edit[i%3][j-1] + 1, edit[(i-1)%3][j] + 1),
                            min(edit[(i-1)%3][j-1] + 1, edit[(i-2)%3][j-2] + 1));
                } else {
                    edit[i%3][j] = min(min(edit[i%3][j-1] + 1, edit[(i-1)%3][j] + 1),
                            edit[(i-1)%3][j-1] + 1);
                }
            }
        }
    }
    return edit[(i-1)%3][j-1];
}

//生成随机字符串
string rand_string(int len){
    srand(time(NULL));
    char a[MAX+1];
    for(int i = 0; i < len; i++){
        a[i] = rand()%26 + 'a';
    }
    a[len] = '\0';
    string str(a);
    return str;
}

// 获取当前时间 (ms)
long getCurrentTime(){
    struct timeval tv;
    gettimeofday(&tv, NULL);
    return tv.tv_sec*1000 + tv.tv_usec/1000;
}

//-----------------------------测试函数------------------------
//测试最短编辑距离函数
void Test_1(){
    string a = "abcdef";
    string b = "abcdef";
    int max_len = edit_length(a, b);
    cout << max_len << endl;
}

// 验证 Trie 树是否完整
void Test_2(){

    //1.创建对象，打开文件
    Trie trie;
    string str;
    ifstream fin;
    fin.open("dict.txt");
    if(!fin){
        cout << "打开文件失败！" << endl;
    }

    //2.建立Trie树
    while(getline(fin, str, '\n')){
        trie.insert(str);
    }
    fin.close();

    //3.验证Trie树的正确性
    fin.open("dict.txt");
    if(!fin){
        cout << "打开文件失败！" << endl;
    }
    while(getline(fin, str, '\n')){
        int count = 0;
        vector<string> word_set;
        trie.search(str, 1, word_set);
        cout << word_set.size() << "  " << str << endl;
    }

}


//测试对于随机字符串搜索结果的正确性
void Test_3(){

    //1.创建对象，打开文件
    Trie trie;
    string str;
    ifstream fin;
    fin.open("dict.txt");
    if(!fin){
        cout << "打开文件失败！" << endl;
    }

    //2.建立Trie树
    long time_1 = getCurrentTime();
    while(getline(fin, str, '\n')){
        trie.insert(str);
    }
    long time_2 = getCurrentTime();
    fin.close();

    //3.产生随机字符串
    string rand_str = rand_string(6);
    //rand_str = "wdeuojyucsalslpd";
    cout << "随机字符串为：" << rand_str << endl;

    //4.利用Trie树计算结果
    vector<string> word_set_1;
    long time_3 = getCurrentTime();
    trie.search(rand_str, 3, word_set_1);
    long time_4 = getCurrentTime();

    //5.利用暴力匹配计算结果
    vector<string> word_set_2;
    vector<string> word_dict;
    fin.open("dict.txt");
    if(!fin){
        cout << "打开文件失败！" << endl;
    }
    while(getline(fin, str, '\n')){
        word_dict.push_back(str);
    }
    int size = word_dict.size();
    long time_5 = getCurrentTime();
    for(int j = 0; j < size; j++){
        if(edit_length(word_dict[j], rand_str) < 3){
            word_set_2.push_back(word_dict[j]);
        }
    }
    long time_6 = getCurrentTime();
    fin.close();

    //6.结果比较
    sort(word_set_1.begin(), word_set_1.end());
    sort(word_set_2.begin(), word_set_2.end());

    cout << "word_set_1的大小：" << word_set_1.size() << endl;
    cout << "结果为：";
    for(int i = 0; i < word_set_1.size(); i++){
        cout << "  " << word_set_1[i];
    }
    cout << endl;

    cout << "word_set_2的大小：" << word_set_2.size() << endl;
    cout << "结果为：";
    for(int i = 0; i < word_set_2.size(); i++){
        cout << "  " << word_set_2[i];
    }
    cout << endl;

    if(word_set_1 == word_set_2){
        cout << "验证正确" << endl;
    } else {
        cout << "验证错误" << endl;
    }

    //7.时间比较
    cout << "建立Trie树用时（ms）：" << time_2 - time_1 << endl;
    cout << "Trie树搜索用时（ms）：" << time_4 - time_3 << endl;
    cout << "暴力搜索用时（ms）："   << time_6 - time_5 << endl;
    cout << "百分比：" << double(time_4 -time_3)/(time_6 - time_5) << endl;
}
int main(){

    //Test_1();
    //Test_2();
    Test_3();
}

refs and see also

如何从零写一个正则表达式引擎？ @

推荐代码: Henry Spencer’s regexp engine regexp.old/regexp.c at master · garyhouston/regexp.old 是很多现代流行的正则引擎的始祖, 解释器实现, 很多新 feature 能扩展得得进去, 也有混合 DFA 的优化

http://whudoc.qiniudn.com/2016/regex.zip @

写了个 80 行的 C++ 模板版。注意啊，regex 的定义包括了 concatenation， alternation（“|”），Kleene closure（“*”），还得有一个ε字符（可近似认为 “?”），expression 还要能嵌套（“(”“)”）。有些例子里缺了 alternation 和嵌套那就不该叫 regex 了。

之所以这么短是因为压根没有 parsing，parsing 多无聊啊。直接构造 regex 的 AST，根本不去打 NFA 的主意。想加什么功能就直接加 type 就行了。

这个是 compile time regex，所以跑起来是 raw speed，很快。你要是要运行时的regex，把那几个模板特化改为一个树状 variant 结构，在树上走就行了，算法（包括那个 continuation 的 trick）都是一样的。

建 NFA 那套做法是 Ken Thompson 推出来的“标准”算法，但是就玩玩而已应该从更简单的学起。学一下 CPS 变换又不会死。

另外把程序写短小紧凑的诀窍就是写成 FP style。我的 80 行中所有函数都只有一个 return 语句。

template <typename Left, typename Right>
struct ConcatExpr;

template <typename Left, typename Right>
struct AltExpr;

template <typename SubExpr>
struct RepeatExpr;

template <char ch>
struct MatchExpr;

template <typename RegExpr>
struct MatchImpl;

struct EpsilonExpr;

template <typename SubExpr>
using OptionalExpr = AltExpr<SubExpr, EpsilonExpr>;

template <typename Left, typename Right>
struct MatchImpl<ConcatExpr<Left, Right>> {
  template <typename Continuation>
  static bool Apply(const char* target, Continuation cont) {
    return MatchImpl<Left>::Apply(target, [cont](const char* rest) -> bool {
      return MatchImpl<Right>::Apply(rest, cont);
    });
  }
};

template <typename Left, typename Right>
struct MatchImpl<AltExpr<Left, Right>> {
  template <typename Continuation>
  static bool Apply(const char* target, Continuation cont) {
    return MatchImpl<Left>::Apply(target, cont) ||
           MatchImpl<Right>::Apply(target, cont);
  }
};

template <typename SubExpr>
struct MatchImpl<RepeatExpr<SubExpr>> {
  template <typename Continuation>
  static bool Apply(const char* target, Continuation cont) {
    return MatchImpl<SubExpr>::Apply(
               target,
               [target, cont](const char* rest) -> bool {
                 return target < rest &&
                     MatchImpl<RepeatExpr<SubExpr>>::Apply(rest, cont);
               }) ||
           cont(target);
  }
};

template <char ch>
struct MatchImpl<MatchExpr<ch>> {
  template <typename Continuation>
  static bool Apply(const char* target, Continuation cont) {
    return *target && *target == ch && cont(target + 1);
  }
};

template <>
struct MatchImpl<EpsilonExpr> {
  template <typename Continuation>
  static bool Apply(const char* target, Continuation cont) {
    return cont(target);
  }
};

template <typename RegExpr>
bool RegexMatch(const char* target) {
  return MatchImpl<RegExpr>::Apply(
      target, [](const char* rest) -> bool { return *rest == '\0'; });
}

template <typename RegExpr>
bool RegexSearch(const char* target) {
  return MatchImpl<RegExpr>::Apply(
             target, [](const char* rest) -> bool { return true; }) ||
         (*target && RegexSearch<RegExpr>(target + 1));
}

#include <cassert>

int main() {
  assert((RegexMatch<ConcatExpr<MatchExpr<'a'>, MatchExpr<'b'>>>("ab")));
  assert((RegexMatch<AltExpr<MatchExpr<'a'>, MatchExpr<'b'>>>("a")));
  assert((RegexMatch<AltExpr<MatchExpr<'a'>, MatchExpr<'b'>>>("b")));
  assert((RegexMatch<RepeatExpr<MatchExpr<'a'>>>("aaaaa")));
  assert((RegexMatch<ConcatExpr<RepeatExpr<MatchExpr<'a'>>, MatchExpr<'b'>>>(
      "aaaaab")));
  assert((
      RegexMatch<ConcatExpr<RepeatExpr<MatchExpr<'a'>>, MatchExpr<'b'>>>("b")));
  assert((RegexSearch<ConcatExpr<RepeatExpr<MatchExpr<'a'>>, MatchExpr<'b'>>>(
      "aaaaabb")));
  assert((RegexMatch<OptionalExpr<MatchExpr<'a'>>>("a")));
  assert((RegexMatch<OptionalExpr<MatchExpr<'a'>>>("")));
  assert((RegexMatch<OptionalExpr<ConcatExpr<MatchExpr<'a'>, MatchExpr<'b'>>>>(
      "ab")));
  assert((RegexMatch<OptionalExpr<ConcatExpr<MatchExpr<'a'>, MatchExpr<'b'>>>>(
      "")));
  assert((!RegexMatch<RepeatExpr<MatchExpr<'a'>>>("aaaaab")));
  assert((RegexMatch<RepeatExpr<OptionalExpr<MatchExpr<'a'>>>>("")));

  return 0;
}

Milo Yip 的正则代码 @

todo

rapidjson/regex.h at regex · miloyip/rapidjson

refs and see also

如何从零写一个正则表达式引擎？ - 知乎

ACM 题集以及各种总结大全！ - 枯槐树下乘凉 - 博客频道 - CSDN.NET
《挑战程序设计竞赛(第2版)》-码农场
演算法筆記
網誌 - BYVoid
hiho 一下第 114 周《Image Encryption》题目分析 - hihoCoder
DSACPP, 数据结构（C++语言版）
程序员如何快速准备面试中的算法 - 结构之法算法之道 - 博客频道 - CSDN.NET
检测单链表中是否有环–快慢指针法 - Linloves - 博客频道 - CSDN.NET
Adoo’s blog - Introduction to Algorithm -third edition @
算法导论——平摊分析
赫夫曼编码 @
赫夫曼编码的正确性

证明赫夫曼编码的正确性需证明贪心算法的两要素：

具有最优子结构

贪心选择性质
《算法导论》笔记汇总 @

仿STL 的二叉搜索树的C++实现

扩展数据结构

C++实现红黑树，仿STL封装

Chapter 13 Red-Black trees (红黑树)

Radix Tree 基数树

算法导论6-3 young tableaus

哈希表（1）

快速排序及C++实现

利用堆来建立优先级队列

排序之插入排序与合并排序-C++实现
refs and see also
- Adoo’s blog - Introduction to Algorithm -third edition @